2021——2022学年湘教版九年级数学下册第1章 圆 单元测试题(Word版含答案)
文档属性
| 名称 | 2021——2022学年湘教版九年级数学下册第1章 圆 单元测试题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 245.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 00:00:00 | ||
图片预览





文档简介
第2章 圆
一、选择题(本大题共8小题,每小题3分,共24分)
1.若☉O的半径为4 cm,点A到圆心O的距离为5 cm,那么点A与☉O的位置关系是( )
A.点A在☉O外 B.点A在☉O上
C.点A在☉O内 D.不能确定
2.已知一个扇形的弧长为10π cm,圆心角是150°,则它的半径为( )
A.12 cm B.10 cm C.8 cm D.6 cm
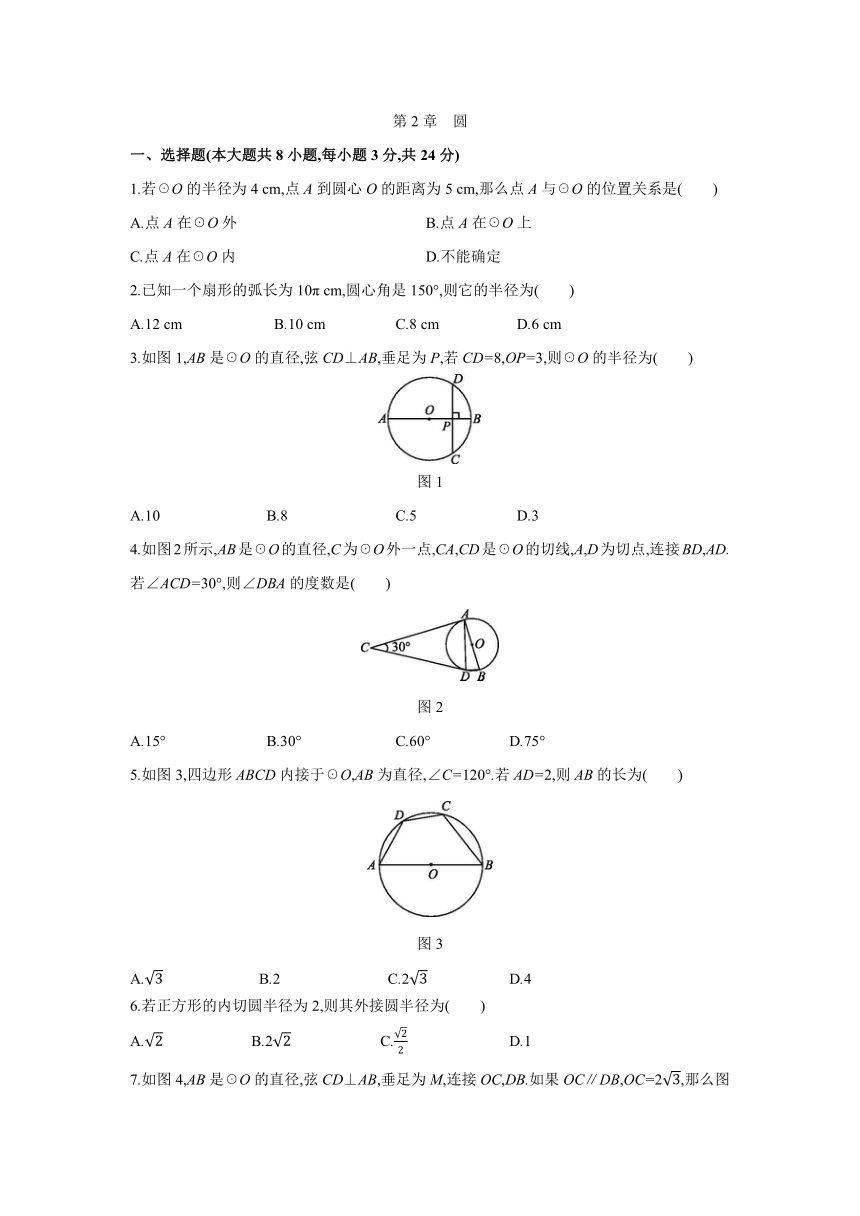
3.如图1,AB是☉O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=3,则☉O的半径为( )
图1
A.10 B.8 C.5 D.3
4.如图2所示,AB是☉O的直径,C为☉O外一点,CA,CD是☉O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的度数是( )
图2
A.15° B.30° C.60° D.75°
5.如图3,四边形ABCD内接于☉O,AB为直径,∠C=120°.若AD=2,则AB的长为( )
图3
A. B.2 C.2 D.4
6.若正方形的内切圆半径为2,则其外接圆半径为( )
A. B.2 C. D.1
7.如图4,AB是☉O的直径,弦CD⊥AB,垂足为M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
图4
A.π B.2π C.3π D.4π
8.如图5,AA1,A1A2,A2A3,A3B,AB分别是五个半圆的直径,两只小虫同时出发,以相同的速度从点A到点B,甲虫沿,,,路线爬行,乙虫沿路线爬行,则下列结论正确的是( )
图5
A.甲先到点B B.乙先到点B
C.甲、乙同时到点B D.无法确定谁先到点B
二、填空题(本大题共8小题,每小题4分,共32分)
9.已知☉O的半径为3 cm,圆心O到直线l的距离是2 cm,则直线l与☉O的位置关系是 .
10.一个扇形的圆心角为120°,半径为2,则这个扇形的面积为 .
11.如图6,PA,PB分别切☉O于点A,B,并与☉O的切线分别相交于C,D两点,已知△PCD的周长等于10 cm,则PA= cm.
图6
12.如图7,AB是☉O的弦,AC是☉O的直径,∠A=35°,过点C的切线与OB的延长线交于点D,则∠D的度数为 .
图7
13.如图8,圆弧形桥拱的跨度AB=24米,拱高CD=9米,那么圆弧形桥拱所在圆的半径是
米.
图8
14.如图9,☉O的半径为6 cm,B为☉O外一点,OB交☉O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在☉O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为
时,BP与☉O相切.
图9
15.如图10,MN是☉O的直径,若∠A=10°,∠PMQ=40°,以PM为边作圆的内接正多边形,则这个正多边形是 边形.
图10
16.如图11,在Rt△AOB中,∠AOB=90°,OA=OB=4,☉O的半径为2,P是AB边上的动点,过点P作☉O的一条切线PQ(Q为切点),则线段PQ长的最小值为 .
图11
三、解答题(共44分)
17.(10分)已知☉O的半径为10 cm,AB,CD是☉O的两条弦,AB∥CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是多少 请画图并计算.
18.(10分)如图12,已知☉O是△ABC的外接圆,AD是☉O的直径,且BD=BC,延长AD到点E,且有∠EBD=∠CAB.
求证:BE是☉O的切线.
图12
19.(12分)如图13,已知AB是☉O的直径,CD与☉O相切于点D,且AD∥OC.
(1)求证:BC是☉O的切线;
(2)延长CO交☉O于点E,若∠CEB=30°,☉O的半径为2,求的长(结果保留π).
图13
20.(12分)如图14,AB是☉O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.(1)求证:EF是☉O的切线;(2)求证:AC2=AB·AD;
(3)若☉O的半径为2,∠ACD=30°,求图中阴影部分的面积.
图14
答案
1.A [解析] ∵☉O的半径为4 cm,点A到圆心O的距离为5 cm,5 cm>4 cm,∴点A在☉O外.故选A.
2.A [解析] 设它的半径为r cm.根据题意,得=10π,解得r=12.
3.C [解析] 如图,连接OD.∵CD=8,∴由垂径定理可得PD=4.∵△OPD是直角三角形,PD=4,OP=3,∴由勾股定理可得OD===5.
4.D [解析] 连接OD.∵CA,CD是☉O的切线,∴OA⊥CA,OD⊥CD,∴∠OAC=∠ODC=90°.
∵∠ACD=30°,∴∠AOD=360°-∠C-∠OAC-∠ODC=150°.∵OB=OD,
∴∠DBA=∠ODB=∠AOD=75°.故选D.
5.D [解析] 如图,连接OD,
∵四边形ABCD是☉O的内接四边形,∴∠A+∠C=180°.∵∠C=120°,∴∠A=60°.
又∵OD=OA,∴△AOD是等边三角形,∴AD=OD=OA.∵AD=2,∴OA=OD=OB=2,
∴AB=2+2=4.故选D.
6.B
7.B [解析] 如图,连接OD,BC,则OD=OB.
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD.
∵OC∥DB,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,∴OD=DB,
∴OD=DB=OB,
∴△BOD是等边三角形,
∴∠BOD=60°,∴∠BOC=60°.
∵DM=CM,∴S△OBC=S△OBD.
∵OC∥DB,∴S△OBD=S△CBD,
∴S△OBC=S△CBD,
∴图中阴影部分的面积=S扇形BOC==2π.
故选B.
8.C [解析] π(AA1+A1A2+A2A3+A3B)=π·AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此甲、乙同时到点B.故选C.
9.相交 [解析] ∵圆心O到直线l的距离是2 cm,小于☉O的半径3 cm,∴直线l与☉O相交.
10. [解析] S==.
11.5 [解析] 设DC与☉O的切点为E.
∵PA,PB都是☉O的切线,
∴PA=PB,同理可得:DE=DA,CE=CB,
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm),
∴PA=PB=5 cm.
故答案为5.
12.20°
13. [解析] 设圆弧形桥拱所在圆的圆心为O,
如图,连接BO,DO.由题意可得AD=BD,DO⊥AB,C,D,O三点在一条直线上.∵AB=24米,拱高CD=9米,∴BD=AD=12米.设BO=x米,则DO=(x-9)米,根据题意可得BD2+DO2=BO2,即122+(x-9)2=x2,解得x=,即圆弧形桥拱所在圆的半径是米.
14.2 s或10 s [解析] 如图,连接OP,∵当OP⊥PB时,BP与☉O相切.
∵AB=OA,OA=OP,
∴OB=2OP,
∴在Rt△OPB中,可得∠B=30°,
∴∠O=60°.
∵OA=6 cm,==2π.
∵圆的周长为12π,
∴当BP与☉O相切时,点P运动的距离为2π或12π-2π=10π,
∴当t=2 s或10 s时,有BP与☉O相切.
故答案为2 s或10 s.
15.六 [解析] 如图,连接QO,PO.
∵QO=PO,
∴∠OPQ=∠OQP.
∵∠PMQ=40°,
∴∠POQ=80°,
∴∠OPQ+∠OQP=180°-80°=100°,∴∠OPQ=∠OQP=50°,∴∠A+∠APO=∠POM=10°+50°=60°.∵PO=OM,∴△POM是等边三角形,∴PM=PO=OM,∴以PM为边作圆的内接正多边形,则这个正多边形是正六边形.
16.2 [解析] 连接OQ,如图所示.
∵PQ是☉O的切线,
∴OQ⊥PQ.
在Rt△POQ中,根据勾股定理,得PQ2=OP2-OQ2.∵OQ为定值,∴当OP最小时,PQ取得最小值.当OP⊥AB时,OP有最小值,此时线段PQ最短.
在Rt△AOB中,由OA=OB=4,
易得OP=4,
∴PQ===2.
故答案为2.
17.解:有两种情况:①圆心O在弦AB和弦CD的同旁,如图①,连接OC,OA,
过点O作OE⊥AB于点E,且直线OE交CD于点F,
∵AB∥CD,
∴OF⊥CD,
∴∠OFC=∠OEA=90°.
∵OE⊥AB,AB=16 cm,
∴AE=BE=8 cm,
同理CF=DF=6 cm,
由勾股定理得:OE===6(cm),
OF===8(cm),
∴EF=OF-OE=2 cm;
②圆心O在弦AB和弦CD之间,如图②,
同(1)可得OE=6 cm,OF=8 cm,
此时EF=OE+OF=14 cm.
综上可知,弦AB和CD之间的距离是2 cm或14 cm.
18.证明:如图,连接OB.
∵BD=BC,
∴=,∠BAD=∠CAB.
∵OA=OB,
∴∠BAD=∠ABO,
∴∠CAB=∠ABO.
∵∠EBD=∠CAB,
∴∠ABO=∠EBD.
∵AD是☉O的直径,
∴∠ABD=90°,即∠ABO+∠OBD=90°,
∴∠EBD +∠OBD=90°,
即∠OBE=90°,∴OB⊥BE.
又∵OB是☉O的半径,
∴BE是☉O的切线.
19.解:(1)证明:连接OD.
∵CD与☉O相切于点D,
∴∠ODC=90°.
∵OD=OA,∴∠OAD=∠ODA.
∵AD∥OC,
∴∠COB=∠OAD,∠COD=∠ODA,
∴∠COB=∠COD.
在△COD和△COB中,
∴△COD≌△COB(SAS),
∴∠ODC=∠OBC=90°,
即OB⊥BC.
又∵OB是☉O的半径,
∴BC是☉O的切线.
(2)∵∠CEB=30°,
∴∠COB=60°.
∵∠COB=∠COD,
∴∠BOD=120°,
∴的长为=π.
20.解:(1)证明:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴AD∥OC.
又∵AD⊥EF,
∴OC⊥EF.
又∵OC是☉O的半径,
∴EF是☉O的切线.
(2)证明:方法1:如图,连接BC.
∵AB是☉O的直径,AD⊥EF,
∴∠ACB=∠ADC=90°.
在△ABC和△ACD中,
∵∠BAC=∠DAC,∠ACB=∠ADC,
∴△ABC∽△ACD,∴=,
即AC2=AB·AD.
方法2:(锐角三角函数法)
∵∠BAC=∠DAC,
∴cos∠BAC=cos∠DAC,
∴=,即AC2=AB·AD.
(3)由(1)知∠ACD+∠ACO=90°.
∵∠ACD=30°,∴∠ACO=60°.
又∵OC=OA,
∴△ACO是等边三角形,
∴AC=OC=2,∠AOC=60°.
在Rt△ADC中,
∵∠ACD=30°,
∴AD=1,CD=,
∴S阴影=S梯形OCDA-S扇形OCA=×(1+2)×-=-.
一、选择题(本大题共8小题,每小题3分,共24分)
1.若☉O的半径为4 cm,点A到圆心O的距离为5 cm,那么点A与☉O的位置关系是( )
A.点A在☉O外 B.点A在☉O上
C.点A在☉O内 D.不能确定
2.已知一个扇形的弧长为10π cm,圆心角是150°,则它的半径为( )
A.12 cm B.10 cm C.8 cm D.6 cm
3.如图1,AB是☉O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=3,则☉O的半径为( )
图1
A.10 B.8 C.5 D.3
4.如图2所示,AB是☉O的直径,C为☉O外一点,CA,CD是☉O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的度数是( )
图2
A.15° B.30° C.60° D.75°
5.如图3,四边形ABCD内接于☉O,AB为直径,∠C=120°.若AD=2,则AB的长为( )
图3
A. B.2 C.2 D.4
6.若正方形的内切圆半径为2,则其外接圆半径为( )
A. B.2 C. D.1
7.如图4,AB是☉O的直径,弦CD⊥AB,垂足为M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
图4
A.π B.2π C.3π D.4π
8.如图5,AA1,A1A2,A2A3,A3B,AB分别是五个半圆的直径,两只小虫同时出发,以相同的速度从点A到点B,甲虫沿,,,路线爬行,乙虫沿路线爬行,则下列结论正确的是( )
图5
A.甲先到点B B.乙先到点B
C.甲、乙同时到点B D.无法确定谁先到点B
二、填空题(本大题共8小题,每小题4分,共32分)
9.已知☉O的半径为3 cm,圆心O到直线l的距离是2 cm,则直线l与☉O的位置关系是 .
10.一个扇形的圆心角为120°,半径为2,则这个扇形的面积为 .
11.如图6,PA,PB分别切☉O于点A,B,并与☉O的切线分别相交于C,D两点,已知△PCD的周长等于10 cm,则PA= cm.
图6
12.如图7,AB是☉O的弦,AC是☉O的直径,∠A=35°,过点C的切线与OB的延长线交于点D,则∠D的度数为 .
图7
13.如图8,圆弧形桥拱的跨度AB=24米,拱高CD=9米,那么圆弧形桥拱所在圆的半径是
米.
图8
14.如图9,☉O的半径为6 cm,B为☉O外一点,OB交☉O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在☉O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为
时,BP与☉O相切.
图9
15.如图10,MN是☉O的直径,若∠A=10°,∠PMQ=40°,以PM为边作圆的内接正多边形,则这个正多边形是 边形.
图10
16.如图11,在Rt△AOB中,∠AOB=90°,OA=OB=4,☉O的半径为2,P是AB边上的动点,过点P作☉O的一条切线PQ(Q为切点),则线段PQ长的最小值为 .
图11
三、解答题(共44分)
17.(10分)已知☉O的半径为10 cm,AB,CD是☉O的两条弦,AB∥CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是多少 请画图并计算.
18.(10分)如图12,已知☉O是△ABC的外接圆,AD是☉O的直径,且BD=BC,延长AD到点E,且有∠EBD=∠CAB.
求证:BE是☉O的切线.
图12
19.(12分)如图13,已知AB是☉O的直径,CD与☉O相切于点D,且AD∥OC.
(1)求证:BC是☉O的切线;
(2)延长CO交☉O于点E,若∠CEB=30°,☉O的半径为2,求的长(结果保留π).
图13
20.(12分)如图14,AB是☉O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.(1)求证:EF是☉O的切线;(2)求证:AC2=AB·AD;
(3)若☉O的半径为2,∠ACD=30°,求图中阴影部分的面积.
图14
答案
1.A [解析] ∵☉O的半径为4 cm,点A到圆心O的距离为5 cm,5 cm>4 cm,∴点A在☉O外.故选A.
2.A [解析] 设它的半径为r cm.根据题意,得=10π,解得r=12.
3.C [解析] 如图,连接OD.∵CD=8,∴由垂径定理可得PD=4.∵△OPD是直角三角形,PD=4,OP=3,∴由勾股定理可得OD===5.
4.D [解析] 连接OD.∵CA,CD是☉O的切线,∴OA⊥CA,OD⊥CD,∴∠OAC=∠ODC=90°.
∵∠ACD=30°,∴∠AOD=360°-∠C-∠OAC-∠ODC=150°.∵OB=OD,
∴∠DBA=∠ODB=∠AOD=75°.故选D.
5.D [解析] 如图,连接OD,
∵四边形ABCD是☉O的内接四边形,∴∠A+∠C=180°.∵∠C=120°,∴∠A=60°.
又∵OD=OA,∴△AOD是等边三角形,∴AD=OD=OA.∵AD=2,∴OA=OD=OB=2,
∴AB=2+2=4.故选D.
6.B
7.B [解析] 如图,连接OD,BC,则OD=OB.
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD.
∵OC∥DB,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,∴OD=DB,
∴OD=DB=OB,
∴△BOD是等边三角形,
∴∠BOD=60°,∴∠BOC=60°.
∵DM=CM,∴S△OBC=S△OBD.
∵OC∥DB,∴S△OBD=S△CBD,
∴S△OBC=S△CBD,
∴图中阴影部分的面积=S扇形BOC==2π.
故选B.
8.C [解析] π(AA1+A1A2+A2A3+A3B)=π·AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此甲、乙同时到点B.故选C.
9.相交 [解析] ∵圆心O到直线l的距离是2 cm,小于☉O的半径3 cm,∴直线l与☉O相交.
10. [解析] S==.
11.5 [解析] 设DC与☉O的切点为E.
∵PA,PB都是☉O的切线,
∴PA=PB,同理可得:DE=DA,CE=CB,
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm),
∴PA=PB=5 cm.
故答案为5.
12.20°
13. [解析] 设圆弧形桥拱所在圆的圆心为O,
如图,连接BO,DO.由题意可得AD=BD,DO⊥AB,C,D,O三点在一条直线上.∵AB=24米,拱高CD=9米,∴BD=AD=12米.设BO=x米,则DO=(x-9)米,根据题意可得BD2+DO2=BO2,即122+(x-9)2=x2,解得x=,即圆弧形桥拱所在圆的半径是米.
14.2 s或10 s [解析] 如图,连接OP,∵当OP⊥PB时,BP与☉O相切.
∵AB=OA,OA=OP,
∴OB=2OP,
∴在Rt△OPB中,可得∠B=30°,
∴∠O=60°.
∵OA=6 cm,==2π.
∵圆的周长为12π,
∴当BP与☉O相切时,点P运动的距离为2π或12π-2π=10π,
∴当t=2 s或10 s时,有BP与☉O相切.
故答案为2 s或10 s.
15.六 [解析] 如图,连接QO,PO.
∵QO=PO,
∴∠OPQ=∠OQP.
∵∠PMQ=40°,
∴∠POQ=80°,
∴∠OPQ+∠OQP=180°-80°=100°,∴∠OPQ=∠OQP=50°,∴∠A+∠APO=∠POM=10°+50°=60°.∵PO=OM,∴△POM是等边三角形,∴PM=PO=OM,∴以PM为边作圆的内接正多边形,则这个正多边形是正六边形.
16.2 [解析] 连接OQ,如图所示.
∵PQ是☉O的切线,
∴OQ⊥PQ.
在Rt△POQ中,根据勾股定理,得PQ2=OP2-OQ2.∵OQ为定值,∴当OP最小时,PQ取得最小值.当OP⊥AB时,OP有最小值,此时线段PQ最短.
在Rt△AOB中,由OA=OB=4,
易得OP=4,
∴PQ===2.
故答案为2.
17.解:有两种情况:①圆心O在弦AB和弦CD的同旁,如图①,连接OC,OA,
过点O作OE⊥AB于点E,且直线OE交CD于点F,
∵AB∥CD,
∴OF⊥CD,
∴∠OFC=∠OEA=90°.
∵OE⊥AB,AB=16 cm,
∴AE=BE=8 cm,
同理CF=DF=6 cm,
由勾股定理得:OE===6(cm),
OF===8(cm),
∴EF=OF-OE=2 cm;
②圆心O在弦AB和弦CD之间,如图②,
同(1)可得OE=6 cm,OF=8 cm,
此时EF=OE+OF=14 cm.
综上可知,弦AB和CD之间的距离是2 cm或14 cm.
18.证明:如图,连接OB.
∵BD=BC,
∴=,∠BAD=∠CAB.
∵OA=OB,
∴∠BAD=∠ABO,
∴∠CAB=∠ABO.
∵∠EBD=∠CAB,
∴∠ABO=∠EBD.
∵AD是☉O的直径,
∴∠ABD=90°,即∠ABO+∠OBD=90°,
∴∠EBD +∠OBD=90°,
即∠OBE=90°,∴OB⊥BE.
又∵OB是☉O的半径,
∴BE是☉O的切线.
19.解:(1)证明:连接OD.
∵CD与☉O相切于点D,
∴∠ODC=90°.
∵OD=OA,∴∠OAD=∠ODA.
∵AD∥OC,
∴∠COB=∠OAD,∠COD=∠ODA,
∴∠COB=∠COD.
在△COD和△COB中,
∴△COD≌△COB(SAS),
∴∠ODC=∠OBC=90°,
即OB⊥BC.
又∵OB是☉O的半径,
∴BC是☉O的切线.
(2)∵∠CEB=30°,
∴∠COB=60°.
∵∠COB=∠COD,
∴∠BOD=120°,
∴的长为=π.
20.解:(1)证明:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴AD∥OC.
又∵AD⊥EF,
∴OC⊥EF.
又∵OC是☉O的半径,
∴EF是☉O的切线.
(2)证明:方法1:如图,连接BC.
∵AB是☉O的直径,AD⊥EF,
∴∠ACB=∠ADC=90°.
在△ABC和△ACD中,
∵∠BAC=∠DAC,∠ACB=∠ADC,
∴△ABC∽△ACD,∴=,
即AC2=AB·AD.
方法2:(锐角三角函数法)
∵∠BAC=∠DAC,
∴cos∠BAC=cos∠DAC,
∴=,即AC2=AB·AD.
(3)由(1)知∠ACD+∠ACO=90°.
∵∠ACD=30°,∴∠ACO=60°.
又∵OC=OA,
∴△ACO是等边三角形,
∴AC=OC=2,∠AOC=60°.
在Rt△ADC中,
∵∠ACD=30°,
∴AD=1,CD=,
∴S阴影=S梯形OCDA-S扇形OCA=×(1+2)×-=-.
