华东师大版数学八年级上册14.2 勾股定理 折叠问题中的应用复习题课件(共13张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册14.2 勾股定理 折叠问题中的应用复习题课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 151.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 08:06:38 | ||
图片预览





文档简介
(共13张PPT)
复习题
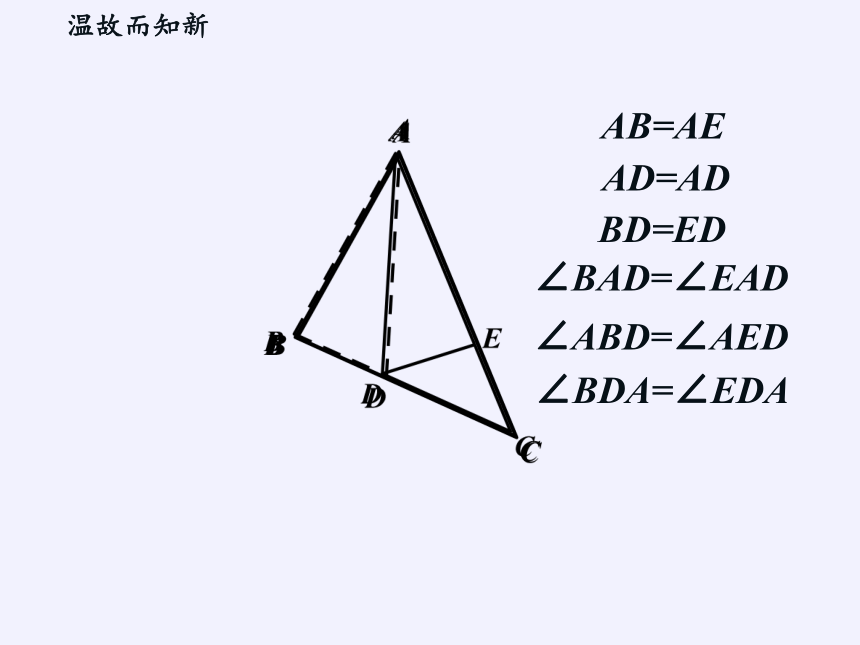
AB=AE
AD=AD
BD=ED
∠BAD=∠EAD
∠BDA=∠EDA
∠ABD=∠AED
温故而知新
勾股定理
折叠问题中的应用
三角形中的折叠
例1.如图,折叠一个直角三角形的纸片,使A与C重合,折痕为DE,若已知AB=4,BC=3,则BE=_______.
三角形中的折叠
例2.如图,有一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边沿直线AD折叠,使点C落在斜边AB上的点E,求CD的长?
1.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上,求CD的长。
巩固新知
2.如图,Rt△ABC中,∠C=90°, D为AB上一点,将△ ABC沿DE折叠,使点B与点A重合,若AC=6,BC=8,求(1)CE的长;(2)折痕DE的长。
巩固新知
发挥你的想象力
长方形可以怎样折叠,要求折叠一次,给出两个已知条件,提出问题,并解答问题。
解题步骤
1、标已知,标问题,明确目标在哪个直角三角形中,设适当的未知数x;
2、利用折叠,找全等。
3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。
4、利用勾股定理,列出方程,解方程,得解。
课堂小结
课堂小结
1、标已知;
2、找相等;
3、设未知,利用勾股定理,列方程;
4、解方程,得解。
希望得到您的批评和指正!
长方形中的折叠
例3:如图所示,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的F处。已知AB=CD=8cm,BC=AD=10cm,求EC的长。
图2
解:由翻折可知:△AFE≌△ADE,
∴AF=AD=10cm,EF=ED,
AB=8 cm,DC=EF+EC=8 cm,
∴在Rt△ABF中,∠B=90°
FC=BC-BF=4 cm
设EC=x cm ,则 EF=DC-EC=(8-x) cm
在Rt△EFC中,∠C=90°
EC +FC =EF
即x +4 =(8-x) ,x=3,
∴EC的长为3 cm.
谢 谢
复习题
AB=AE
AD=AD
BD=ED
∠BAD=∠EAD
∠BDA=∠EDA
∠ABD=∠AED
温故而知新
勾股定理
折叠问题中的应用
三角形中的折叠
例1.如图,折叠一个直角三角形的纸片,使A与C重合,折痕为DE,若已知AB=4,BC=3,则BE=_______.
三角形中的折叠
例2.如图,有一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边沿直线AD折叠,使点C落在斜边AB上的点E,求CD的长?
1.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上,求CD的长。
巩固新知
2.如图,Rt△ABC中,∠C=90°, D为AB上一点,将△ ABC沿DE折叠,使点B与点A重合,若AC=6,BC=8,求(1)CE的长;(2)折痕DE的长。
巩固新知
发挥你的想象力
长方形可以怎样折叠,要求折叠一次,给出两个已知条件,提出问题,并解答问题。
解题步骤
1、标已知,标问题,明确目标在哪个直角三角形中,设适当的未知数x;
2、利用折叠,找全等。
3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。
4、利用勾股定理,列出方程,解方程,得解。
课堂小结
课堂小结
1、标已知;
2、找相等;
3、设未知,利用勾股定理,列方程;
4、解方程,得解。
希望得到您的批评和指正!
长方形中的折叠
例3:如图所示,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的F处。已知AB=CD=8cm,BC=AD=10cm,求EC的长。
图2
解:由翻折可知:△AFE≌△ADE,
∴AF=AD=10cm,EF=ED,
AB=8 cm,DC=EF+EC=8 cm,
∴在Rt△ABF中,∠B=90°
FC=BC-BF=4 cm
设EC=x cm ,则 EF=DC-EC=(8-x) cm
在Rt△EFC中,∠C=90°
EC +FC =EF
即x +4 =(8-x) ,x=3,
∴EC的长为3 cm.
谢 谢
