2021-2022学年湘教版八年级上册期末考试模拟卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年湘教版八年级上册期末考试模拟卷(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 754.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 09:45:10 | ||
图片预览



文档简介
湘教版初二上学期期末考试模拟卷二
选择题(每小题3分,共30分)
1.在,,,,a+,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.如果,那么下列不等式正确的是
A. B. C. D.
3.下列各式变形正确的是( )
A.﹣= B.=
C.= D.=
4.解分式方程时,去分母化为一元一次方程,正确的是
A. B. C. D.
5.已知实数a在数轴上的位置如图所示,则化简|a|+的结果为( )
A.1 B.﹣1 C.1﹣2a D.2a﹣1
6.若一个三角形的两边长分别为、,则它的第三边的长可能是
A. B. C. D.
7.的计算结果为
A. B. C. D.
8.如图,在中,的垂直平分线交于点,交于点,若,,则的周长为
A.8 B.11 C.16 D.17
9.一辆货车送货上山,并按原路下山.上山速度为千米时,下山速度为千米时.则货车上、下山的平均速度为 千米时.
A. B. C. D.
10.如图,在和中,,,,,连接,交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为
A.4 B.3 C.2 D.1
二、填空题(每小题3分,共24分)
11.原子很小,1个氧原子的直径大约为,将0.000000000148用科学记数法表示为 .
若(m+1)x|m|+2>0是关于x的一元一次不等式,则m= .
13.如图,中,,,为延长线上一点,点在上,且,若,则 度.
14.计算的结果是 .
15.分式与通分后的结果是 .
16.若二次根式是最简二次根式,则最小的正整数a=
17.已知不等式组无解,则a的取值范围为 .
18.使得关于x的分式方程﹣=1的解为负整数,且使得关于x的不等式组有且仅有5个整数解的所有k的和为 .
三、解答题(7小题,共66分)
19.计算:|﹣2|﹣(1+)0+﹣
20.先化简,再求值:,其中.
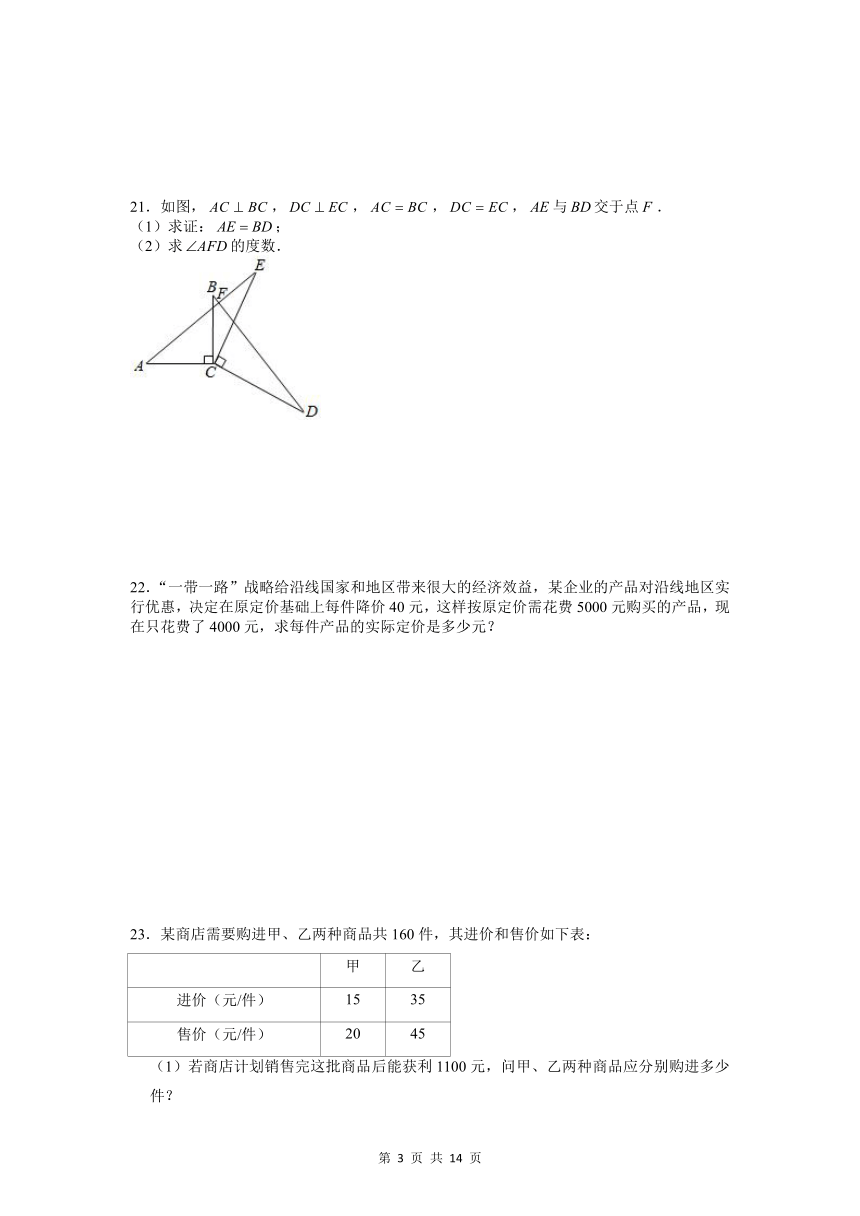
21.如图,,,,,与交于点.
(1)求证:;
(2)求的度数.
22.“一带一路”战略给沿线国家和地区带来很大的经济效益,某企业的产品对沿线地区实行优惠,决定在原定价基础上每件降价40元,这样按原定价需花费5000元购买的产品,现在只花费了4000元,求每件产品的实际定价是多少元?
23.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
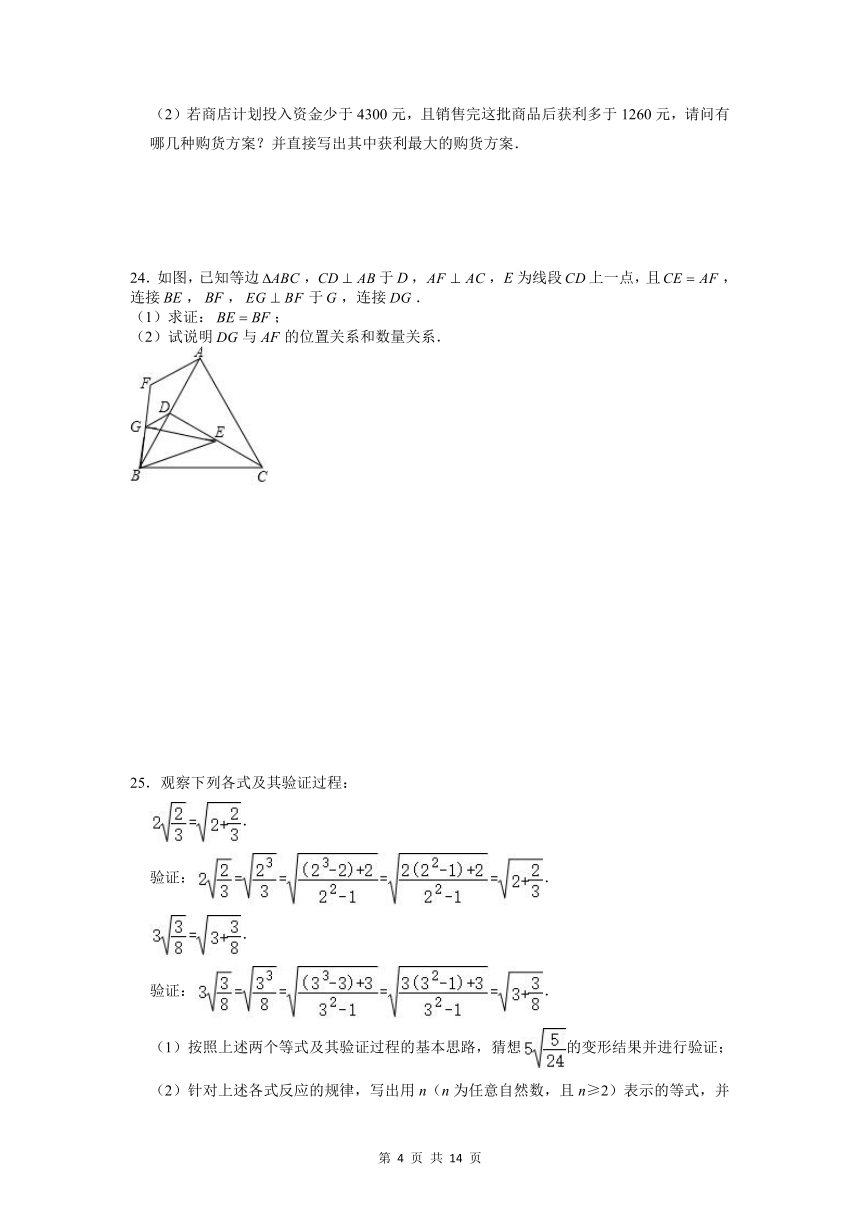
24.如图,已知等边,于,,为线段上一点,且,连接,,于,连接.
(1)求证:;
(2)试说明与的位置关系和数量关系.
25.观察下列各式及其验证过程:
.
验证:.
.
验证:.
(1)按照上述两个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
(2)针对上述各式反应的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并说明它成立.
湘教版初二上学期期末考试模拟卷二(答案)
选择题(每小题3分,共30分)
1.在,,,,a+,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
解:,,﹣,,,其中分式有:,,共3个.
故选:C.
2.如果,那么下列不等式正确的是
A. B. C. D.
、,
,故本选项符合题意;
、,
,故本选项不符合题意;
、,
,故本选项不符合题意;
、,
,故本选项不符合题意;
故选:.
3.下列各式变形正确的是( )
A.﹣= B.=
C.= D.=
3.解:A、原式=,不符合题意;
B、当a≠0时,原式=,不符合题意;
C、原式=,符合题意;
D、当x≠0时,原式=,不符合题意,
故选:C.
4.解分式方程时,去分母化为一元一次方程,正确的是
A. B. C. D.
解:方程两边都乘以,得
,
故选:.
5.已知实数a在数轴上的位置如图所示,则化简|a|+的结果为( )
A.1 B.﹣1 C.1﹣2a D.2a﹣1
解:由数轴可得,
0<a<1,
则a﹣1<0,a>0,
∴原式=|a|+|a﹣1|=a﹣a+1=1.
故选:A.
6.若一个三角形的两边长分别为、,则它的第三边的长可能是
A. B. C. D.
解:设第三边长为,根据三角形的三边关系可得:
,
解得:,
故选:.
7.的计算结果为
A. B. C. D.
解:原式
.
故选:.
8.如图,在中,的垂直平分线交于点,交于点,若,,则的周长为
A.8 B.11 C.16 D.17
解:垂直平分,
,
的周长
.
故选:.
9.一辆货车送货上山,并按原路下山.上山速度为千米时,下山速度为千米时.则货车上、下山的平均速度为 千米时.
A. B. C. D.
设上山的路程为千米,
则上山的时间小时,下山的时间为小时,
则上、下山的平均速度千米时.
故选:.
10.如图,在和中,,,,,连接,交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为
A.4 B.3 C.2 D.1
解:,
,
即,
在和中,,
,
,,①正确;
,
由三角形的外角性质得:,
,②正确;
作于,于,如图2所示:
则,
在和中,,
,
,
平分,④正确;
,
当时,才平分,
假设
,
,
平分,
,
在和中,,
,
,
与矛盾,
③错误;
正确的个数有3个;
故选:.
二、填空题(每小题3分,共24分)
11.原子很小,1个氧原子的直径大约为,将0.000000000148用科学记数法表示为 .
解:.
故答案为:.
若(m+1)x|m|+2>0是关于x的一元一次不等式,则m= .
解:∵(m+1)x|m|+2>0是关于x的一元一次不等式,
∴m+1≠0,|m|=1.
解得:m=1.
故答案为:1.
13.如图,中,,,为延长线上一点,点在上,且,若,则 度.
解:在与中,,
.
;
,,
,
;
故答案为:70.
14.计算的结果是 .
解:原式
.
故答案为:.
15.分式与通分后的结果是 .
解:∵x2﹣3x=x(x﹣3),x2﹣9=(x﹣3)(x+3),
∴分式==,
分式==.
故答案为,.
16.若二次根式是最简二次根式,则最小的正整数a=
解:二次根式是最简二次根式,则最小的正整数a=2,
故答案为:2.
17.已知不等式组无解,则a的取值范围为 .
解:∵不等式组无解,
∴a﹣1≤1,
解得:a≤2,
故答案为:a≤2.
18.使得关于x的分式方程﹣=1的解为负整数,且使得关于x的不等式组有且仅有5个整数解的所有k的和为 .
18.解:解分式方程﹣=1,可得x=1﹣2k,
∵分式方程﹣=1的解为负整数,
∴1﹣2k<0,
∴k>,
又∵x≠﹣1,
∴1﹣2k≠﹣1,
∴k≠1,
解不等式组,可得,
∵不等式组有5个整数解,
∴1≤<2,
解得0≤k<4,
∴<k<4且k≠1,
∴k的值为1.5或2或2.5或3或3.5,
∴符合题意的所有k的和为12.5,
故答案为:12.5.
三、解答题(7小题,共66分)
19.计算:|﹣2|﹣(1+)0+﹣
19.解:原式==2﹣1+2﹣=.
20.先化简,再求值:,其中.
解:
,
当时,原式.
21.如图,,,,,与交于点.
(1)求证:;
(2)求的度数.
解:(1),,
,
,
在和中,
,
,
;
(2)设与交于点,
,
,
,
,
,
,
.
22.“一带一路”战略给沿线国家和地区带来很大的经济效益,某企业的产品对沿线地区实行优惠,决定在原定价基础上每件降价40元,这样按原定价需花费5000元购买的产品,现在只花费了4000元,求每件产品的实际定价是多少元?
解:设每件产品的实际定价是元,则原定价为元,
由题意,得
.
解得.
经检验是原方程的解,且符合题意.
答:每件产品的实际定价是160元.
23.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
解:(1)设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:.
解得:.
答:甲种商品购进100件,乙种商品购进60件.
(2)设甲种商品购进a件,则乙种商品购进(160﹣a)件.
根据题意得.
解不等式组,得65<a<68.
∵a为非负整数,∴a取66,67.
∴160﹣a相应取94,93.
方案一:甲种商品购进66件,乙种商品购进94件.
方案二:甲种商品购进67件,乙种商品购进93件.
答:有两种购货方案,其中获利最大的是方案一.
24.如图,已知等边,于,,为线段上一点,且,连接,,于,连接.
(1)求证:;
(2)试说明与的位置关系和数量关系.
证明:(1)是等边三角形
,
,
,,
,且,
(2),
理由如下:
连接,
,
,且
是等边三角形,且
,且
,
25.观察下列各式及其验证过程:
.
验证:.
.
验证:.
(1)按照上述两个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
(2)针对上述各式反应的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并说明它成立.
解:(1)5=
验证:5====;
(2)n=,
证明:n====.
选择题(每小题3分,共30分)
1.在,,,,a+,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.如果,那么下列不等式正确的是
A. B. C. D.
3.下列各式变形正确的是( )
A.﹣= B.=
C.= D.=
4.解分式方程时,去分母化为一元一次方程,正确的是
A. B. C. D.
5.已知实数a在数轴上的位置如图所示,则化简|a|+的结果为( )
A.1 B.﹣1 C.1﹣2a D.2a﹣1
6.若一个三角形的两边长分别为、,则它的第三边的长可能是
A. B. C. D.
7.的计算结果为
A. B. C. D.
8.如图,在中,的垂直平分线交于点,交于点,若,,则的周长为
A.8 B.11 C.16 D.17
9.一辆货车送货上山,并按原路下山.上山速度为千米时,下山速度为千米时.则货车上、下山的平均速度为 千米时.
A. B. C. D.
10.如图,在和中,,,,,连接,交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为
A.4 B.3 C.2 D.1
二、填空题(每小题3分,共24分)
11.原子很小,1个氧原子的直径大约为,将0.000000000148用科学记数法表示为 .
若(m+1)x|m|+2>0是关于x的一元一次不等式,则m= .
13.如图,中,,,为延长线上一点,点在上,且,若,则 度.
14.计算的结果是 .
15.分式与通分后的结果是 .
16.若二次根式是最简二次根式,则最小的正整数a=
17.已知不等式组无解,则a的取值范围为 .
18.使得关于x的分式方程﹣=1的解为负整数,且使得关于x的不等式组有且仅有5个整数解的所有k的和为 .
三、解答题(7小题,共66分)
19.计算:|﹣2|﹣(1+)0+﹣
20.先化简,再求值:,其中.
21.如图,,,,,与交于点.
(1)求证:;
(2)求的度数.
22.“一带一路”战略给沿线国家和地区带来很大的经济效益,某企业的产品对沿线地区实行优惠,决定在原定价基础上每件降价40元,这样按原定价需花费5000元购买的产品,现在只花费了4000元,求每件产品的实际定价是多少元?
23.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
24.如图,已知等边,于,,为线段上一点,且,连接,,于,连接.
(1)求证:;
(2)试说明与的位置关系和数量关系.
25.观察下列各式及其验证过程:
.
验证:.
.
验证:.
(1)按照上述两个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
(2)针对上述各式反应的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并说明它成立.
湘教版初二上学期期末考试模拟卷二(答案)
选择题(每小题3分,共30分)
1.在,,,,a+,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
解:,,﹣,,,其中分式有:,,共3个.
故选:C.
2.如果,那么下列不等式正确的是
A. B. C. D.
、,
,故本选项符合题意;
、,
,故本选项不符合题意;
、,
,故本选项不符合题意;
、,
,故本选项不符合题意;
故选:.
3.下列各式变形正确的是( )
A.﹣= B.=
C.= D.=
3.解:A、原式=,不符合题意;
B、当a≠0时,原式=,不符合题意;
C、原式=,符合题意;
D、当x≠0时,原式=,不符合题意,
故选:C.
4.解分式方程时,去分母化为一元一次方程,正确的是
A. B. C. D.
解:方程两边都乘以,得
,
故选:.
5.已知实数a在数轴上的位置如图所示,则化简|a|+的结果为( )
A.1 B.﹣1 C.1﹣2a D.2a﹣1
解:由数轴可得,
0<a<1,
则a﹣1<0,a>0,
∴原式=|a|+|a﹣1|=a﹣a+1=1.
故选:A.
6.若一个三角形的两边长分别为、,则它的第三边的长可能是
A. B. C. D.
解:设第三边长为,根据三角形的三边关系可得:
,
解得:,
故选:.
7.的计算结果为
A. B. C. D.
解:原式
.
故选:.
8.如图,在中,的垂直平分线交于点,交于点,若,,则的周长为
A.8 B.11 C.16 D.17
解:垂直平分,
,
的周长
.
故选:.
9.一辆货车送货上山,并按原路下山.上山速度为千米时,下山速度为千米时.则货车上、下山的平均速度为 千米时.
A. B. C. D.
设上山的路程为千米,
则上山的时间小时,下山的时间为小时,
则上、下山的平均速度千米时.
故选:.
10.如图,在和中,,,,,连接,交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为
A.4 B.3 C.2 D.1
解:,
,
即,
在和中,,
,
,,①正确;
,
由三角形的外角性质得:,
,②正确;
作于,于,如图2所示:
则,
在和中,,
,
,
平分,④正确;
,
当时,才平分,
假设
,
,
平分,
,
在和中,,
,
,
与矛盾,
③错误;
正确的个数有3个;
故选:.
二、填空题(每小题3分,共24分)
11.原子很小,1个氧原子的直径大约为,将0.000000000148用科学记数法表示为 .
解:.
故答案为:.
若(m+1)x|m|+2>0是关于x的一元一次不等式,则m= .
解:∵(m+1)x|m|+2>0是关于x的一元一次不等式,
∴m+1≠0,|m|=1.
解得:m=1.
故答案为:1.
13.如图,中,,,为延长线上一点,点在上,且,若,则 度.
解:在与中,,
.
;
,,
,
;
故答案为:70.
14.计算的结果是 .
解:原式
.
故答案为:.
15.分式与通分后的结果是 .
解:∵x2﹣3x=x(x﹣3),x2﹣9=(x﹣3)(x+3),
∴分式==,
分式==.
故答案为,.
16.若二次根式是最简二次根式,则最小的正整数a=
解:二次根式是最简二次根式,则最小的正整数a=2,
故答案为:2.
17.已知不等式组无解,则a的取值范围为 .
解:∵不等式组无解,
∴a﹣1≤1,
解得:a≤2,
故答案为:a≤2.
18.使得关于x的分式方程﹣=1的解为负整数,且使得关于x的不等式组有且仅有5个整数解的所有k的和为 .
18.解:解分式方程﹣=1,可得x=1﹣2k,
∵分式方程﹣=1的解为负整数,
∴1﹣2k<0,
∴k>,
又∵x≠﹣1,
∴1﹣2k≠﹣1,
∴k≠1,
解不等式组,可得,
∵不等式组有5个整数解,
∴1≤<2,
解得0≤k<4,
∴<k<4且k≠1,
∴k的值为1.5或2或2.5或3或3.5,
∴符合题意的所有k的和为12.5,
故答案为:12.5.
三、解答题(7小题,共66分)
19.计算:|﹣2|﹣(1+)0+﹣
19.解:原式==2﹣1+2﹣=.
20.先化简,再求值:,其中.
解:
,
当时,原式.
21.如图,,,,,与交于点.
(1)求证:;
(2)求的度数.
解:(1),,
,
,
在和中,
,
,
;
(2)设与交于点,
,
,
,
,
,
,
.
22.“一带一路”战略给沿线国家和地区带来很大的经济效益,某企业的产品对沿线地区实行优惠,决定在原定价基础上每件降价40元,这样按原定价需花费5000元购买的产品,现在只花费了4000元,求每件产品的实际定价是多少元?
解:设每件产品的实际定价是元,则原定价为元,
由题意,得
.
解得.
经检验是原方程的解,且符合题意.
答:每件产品的实际定价是160元.
23.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
解:(1)设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:.
解得:.
答:甲种商品购进100件,乙种商品购进60件.
(2)设甲种商品购进a件,则乙种商品购进(160﹣a)件.
根据题意得.
解不等式组,得65<a<68.
∵a为非负整数,∴a取66,67.
∴160﹣a相应取94,93.
方案一:甲种商品购进66件,乙种商品购进94件.
方案二:甲种商品购进67件,乙种商品购进93件.
答:有两种购货方案,其中获利最大的是方案一.
24.如图,已知等边,于,,为线段上一点,且,连接,,于,连接.
(1)求证:;
(2)试说明与的位置关系和数量关系.
证明:(1)是等边三角形
,
,
,,
,且,
(2),
理由如下:
连接,
,
,且
是等边三角形,且
,且
,
25.观察下列各式及其验证过程:
.
验证:.
.
验证:.
(1)按照上述两个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
(2)针对上述各式反应的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并说明它成立.
解:(1)5=
验证:5====;
(2)n=,
证明:n====.
同课章节目录
