第二章点、直线、平面之间的位置关系>>本章综合
文档属性
| 名称 | 第二章点、直线、平面之间的位置关系>>本章综合 |
|
|
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-25 00:00:00 | ||
图片预览



文档简介
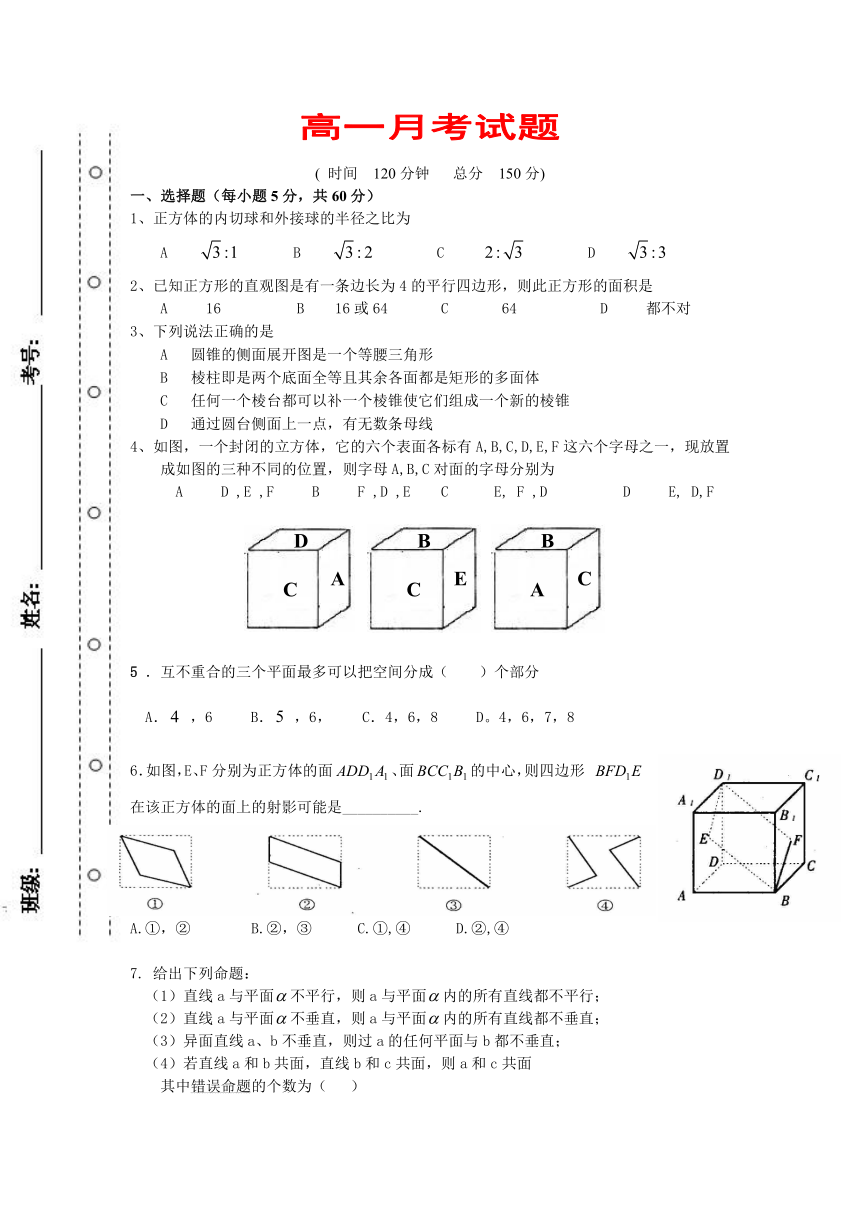
高一月考试题
( 时间 120分钟 总分 150分)
一、选择题(每小题5分,共60分)
1、正方体的内切球和外接球的半径之比为
A B C D
2、已知正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积是
A 16 B 16或64 C 64 D 都不对
3、下列说法正确的是
A 圆锥的侧面展开图是一个等腰三角形
B 棱柱即是两个底面全等且其余各面都是矩形的多面体
C 任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D 通过圆台侧面上一点,有无数条母线
4、如图,一个封闭的立方体,它的六个表面各标有A,B,C,D,E,F这六个字母之一,现放置成如图的三种不同的位置,则字母A,B,C对面的字母分别为
A D ,E ,F B F ,D ,E C E, F ,D D E, D,F
5 .互不重合的三个平面最多可以把空间分成( )个部分
A. ,6 B. ,6, C.4,6,8 D。4,6,7,8
6.如图,E、F分别为正方体的面、面的中心,则四边形 在该正方体的面上的射影可能是__________.
A.①,② B.②,③ C.①,④ D.②,④
7. 给出下列命题:
(1)直线a与平面不平行,则a与平面内的所有直线都不平行;
(2)直线a与平面不垂直,则a与平面内的所有直线都不垂直;
(3)异面直线a、b不垂直,则过a的任何平面与b都不垂直;
(4)若直线a和b共面,直线b和c共面,则a和c共面
其中错误命题的个数为( )
(A)0 (B) 1 (C)2 (D)3
8.直线a,b,c及平面α,β,γ,下列命题正确的是( )
A、若aα,bα,c⊥a, c⊥b 则c⊥α B、若bα, a//b 则 a//α
C、若a//α,α∩β=b 则a//b D、若a⊥α, b⊥α 则a//b
9.直线与平面所成角为,,则与所成角最小()度,最大()度。
A.0,30 B.30, 60 C.30, 90 D.60,90
10. 4中心)中,分别是 的中点,为上任意一点,则直线与所成的角的大小是( ) A. B. C. D.随点的变化而变化。
11..在四面体中,已知棱的长为,其余各棱长都为,则二面角的余弦值为( )
A. B. C. D.
12. .把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时,直线和平面所成的角的大小为( )度。
A. B. C. D.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每小题4分,共16分)
13.半径为R的半圆卷成一个圆锥,则它的体积为________________.
14.(如图)它是一正方体展开图,将它还原为正方体后,AB,CD,EF,GH四条线段所在直线为异面直线的有_______________。
15.空间四边形中,分别是的中点,则与的
位置关系是_____________;四边形是__________形;当___________时,四边形是菱形;当___________时,四边形是矩形;当___________时,四边形是正方形。
16.在正三棱锥(顶点在底面的射影是底面正三角形的中心)中,,过作与分别交于和的截面,则截面的周长的最小值是_______
三、解答题(本大题共6小题,共74分)。
17.已知直线,且直线与都相交,求证:直线共面。
18.已知为空间四边形的边上的点,
且.求证:.
19(如图)正方形SABC中,,E,D分别为AB,CB的中点,SB交DE于G,沿SE,SD,DE折叠成一四面体V-SDE,A,B,C重合于一点V.
(1)。找出折叠后的面面垂直,并说明理由。
(2)。求VG与面SDE所成角的余弦。 S A
E
C B
D
20.在长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a ,E、F分别是A1B1、B1C1的中点
求:(1)AC1和B1D1所成的角
(2)EF和AD1所成的角的正弦。
21. 如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC=2(1)求证:平面AEF⊥平PBC;(2)求二面角P—BC—A的大小;(3)求三棱锥P—AEF的体积.
22.P为三角形ABC所在平面外一点,过P做PO垂直ABC所在平面,O为垂足。
(1).若PA垂直BC,PB垂直AC, 试探究O的位置(4分)
。(2).若PA,PB,PC与面ABC所成角相等,试探究O的位置。(5分)
(3).若P-AC-BD与P-AB-C大小相等,试探究O的位置。(5分
( 时间 120分钟 总分 150分)
一、选择题(每小题5分,共60分)
1、正方体的内切球和外接球的半径之比为
A B C D
2、已知正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积是
A 16 B 16或64 C 64 D 都不对
3、下列说法正确的是
A 圆锥的侧面展开图是一个等腰三角形
B 棱柱即是两个底面全等且其余各面都是矩形的多面体
C 任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D 通过圆台侧面上一点,有无数条母线
4、如图,一个封闭的立方体,它的六个表面各标有A,B,C,D,E,F这六个字母之一,现放置成如图的三种不同的位置,则字母A,B,C对面的字母分别为
A D ,E ,F B F ,D ,E C E, F ,D D E, D,F
5 .互不重合的三个平面最多可以把空间分成( )个部分
A. ,6 B. ,6, C.4,6,8 D。4,6,7,8
6.如图,E、F分别为正方体的面、面的中心,则四边形 在该正方体的面上的射影可能是__________.
A.①,② B.②,③ C.①,④ D.②,④
7. 给出下列命题:
(1)直线a与平面不平行,则a与平面内的所有直线都不平行;
(2)直线a与平面不垂直,则a与平面内的所有直线都不垂直;
(3)异面直线a、b不垂直,则过a的任何平面与b都不垂直;
(4)若直线a和b共面,直线b和c共面,则a和c共面
其中错误命题的个数为( )
(A)0 (B) 1 (C)2 (D)3
8.直线a,b,c及平面α,β,γ,下列命题正确的是( )
A、若aα,bα,c⊥a, c⊥b 则c⊥α B、若bα, a//b 则 a//α
C、若a//α,α∩β=b 则a//b D、若a⊥α, b⊥α 则a//b
9.直线与平面所成角为,,则与所成角最小()度,最大()度。
A.0,30 B.30, 60 C.30, 90 D.60,90
10. 4中心)中,分别是 的中点,为上任意一点,则直线与所成的角的大小是( ) A. B. C. D.随点的变化而变化。
11..在四面体中,已知棱的长为,其余各棱长都为,则二面角的余弦值为( )
A. B. C. D.
12. .把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时,直线和平面所成的角的大小为( )度。
A. B. C. D.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每小题4分,共16分)
13.半径为R的半圆卷成一个圆锥,则它的体积为________________.
14.(如图)它是一正方体展开图,将它还原为正方体后,AB,CD,EF,GH四条线段所在直线为异面直线的有_______________。
15.空间四边形中,分别是的中点,则与的
位置关系是_____________;四边形是__________形;当___________时,四边形是菱形;当___________时,四边形是矩形;当___________时,四边形是正方形。
16.在正三棱锥(顶点在底面的射影是底面正三角形的中心)中,,过作与分别交于和的截面,则截面的周长的最小值是_______
三、解答题(本大题共6小题,共74分)。
17.已知直线,且直线与都相交,求证:直线共面。
18.已知为空间四边形的边上的点,
且.求证:.
19(如图)正方形SABC中,,E,D分别为AB,CB的中点,SB交DE于G,沿SE,SD,DE折叠成一四面体V-SDE,A,B,C重合于一点V.
(1)。找出折叠后的面面垂直,并说明理由。
(2)。求VG与面SDE所成角的余弦。 S A
E
C B
D
20.在长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a ,E、F分别是A1B1、B1C1的中点
求:(1)AC1和B1D1所成的角
(2)EF和AD1所成的角的正弦。
21. 如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC=2(1)求证:平面AEF⊥平PBC;(2)求二面角P—BC—A的大小;(3)求三棱锥P—AEF的体积.
22.P为三角形ABC所在平面外一点,过P做PO垂直ABC所在平面,O为垂足。
(1).若PA垂直BC,PB垂直AC, 试探究O的位置(4分)
。(2).若PA,PB,PC与面ABC所成角相等,试探究O的位置。(5分)
(3).若P-AC-BD与P-AB-C大小相等,试探究O的位置。(5分
