2021-2022学年人教版九年级数学上册24.2 点和圆、直线和圆的位置关系 同步培优(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.2 点和圆、直线和圆的位置关系 同步培优(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 489.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 22:06:50 | ||
图片预览


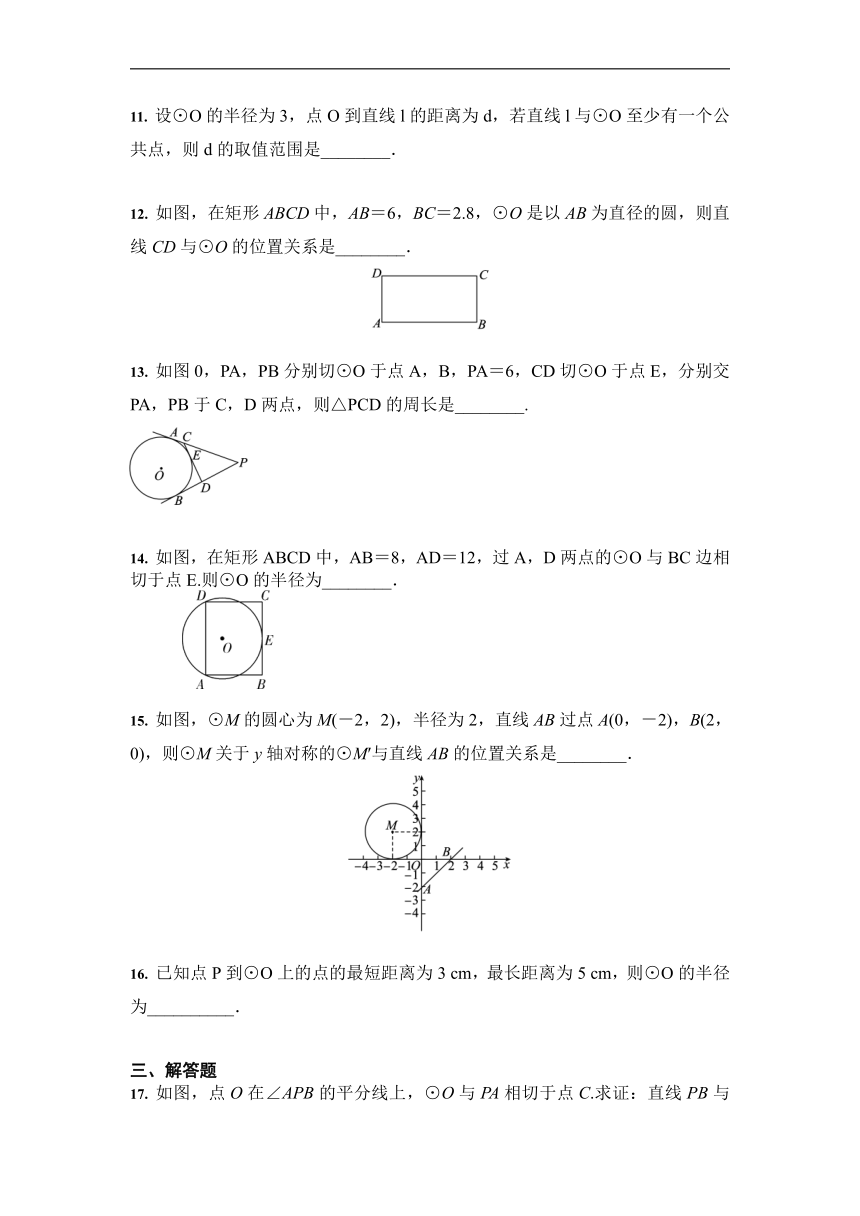

文档简介
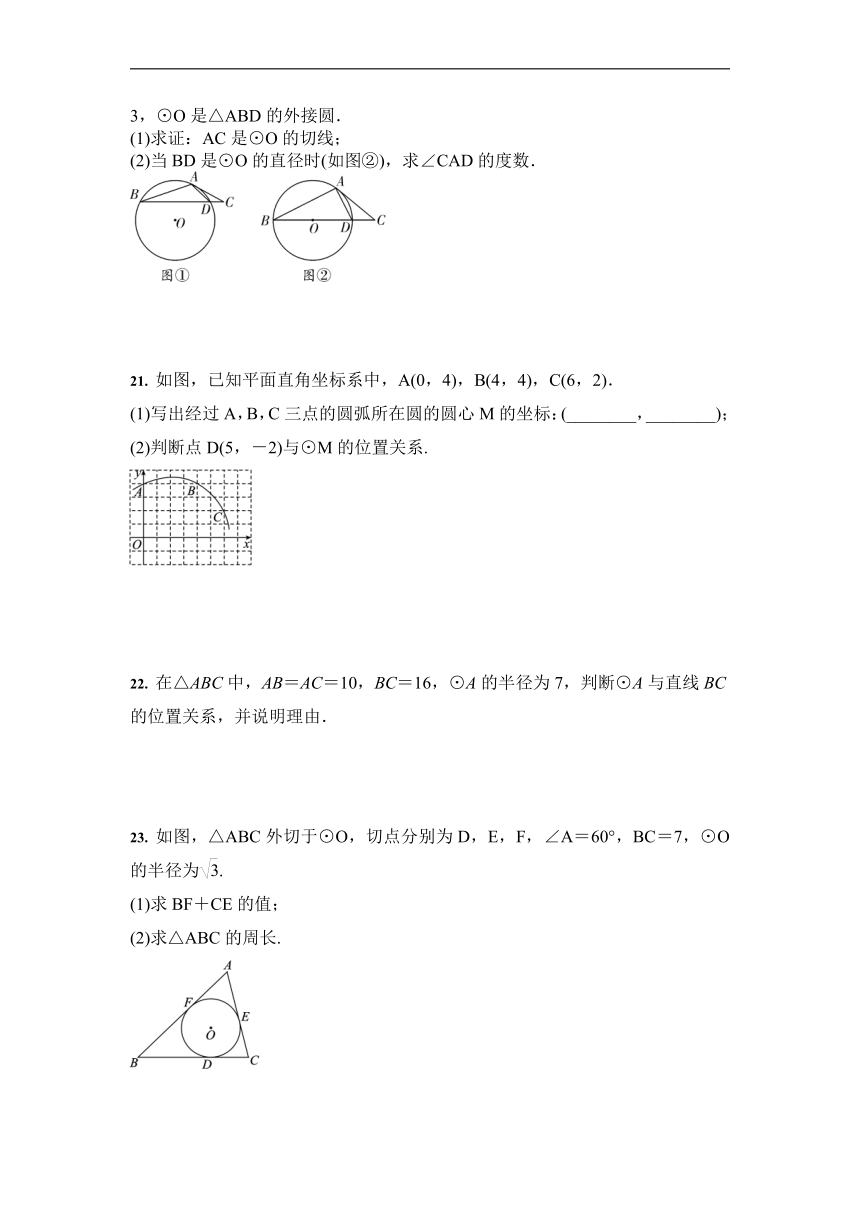
人教版九年级上册 24.2 点和圆、直线和圆的位置关系 同步培优
一、选择题
1. 2019·益阳如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD
C.AB⊥PD D.AB平分PD
2. 已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )
A.1 B.2
C.3 D.4
3. 如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1 B.1或5 C.3 D.5
4. 平面上⊙O与四条直线l1,l2,l3,l4的位置关系如图.若⊙O的半径为2 cm,且点O到其中一条直线的距离为2.2 cm,则这条直线是( )
A.ll B.l2 C.l3 D.l4
5. 如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为( )
A.54° B.36° C.32° D.27°
6. 已知⊙O的面积为9π cm2,若点O到直线l的距离为π cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
7. 已知:在△ABC中,AB=AC,求证:∠B<90°.下面写出了用反证法证明这个命题过程中的四个推理步骤:①因为∠B+∠C≥180°与三角形内角和定理相矛盾;②所以∠B<90°;③假设∠B≥90°;④由AB=AC,得∠C=∠B≥90°,即∠B+∠C≥180°.这四个步骤正确的顺序应是( )
A.①②③④ B.③④②①
C.③④①② D.④③②①
8. 2020·武汉模拟 在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(-10,1)与⊙O的位置关系为( )
A.点P在⊙O上 B.点P在⊙O外
C.点P在⊙O内 D.无法确定
二、填空题
9. 如图,PA,PB是☉O的切线,A,B为切点,点C,D在☉O上.若∠P=102°,则∠A+∠C= .
10. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为 .
11. 设⊙O的半径为3,点O到直线l的距离为d,若直线l与⊙O至少有一个公共点,则d的取值范围是________.
12. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线CD与⊙O的位置关系是________.
13. 如图0,PA,PB分别切⊙O于点A,B,PA=6,CD切⊙O于点E,分别交PA,PB于C,D两点,则△PCD的周长是________.
14. 如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E.则⊙O的半径为________.
15. 如图,⊙M的圆心为M(-2,2),半径为2,直线AB过点A(0,-2),B(2,0),则⊙M关于y轴对称的⊙M′与直线AB的位置关系是________.
16. 已知点P到⊙O上的点的最短距离为3 cm,最长距离为5 cm,则⊙O的半径为__________.
三、解答题
17. 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切.
18. 如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能不能接收到信号,并说明理由.
图
19. 2018·邵阳 如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
20. 如图①,在△ABC中,点D在边BC上,∠ABC ∶∠ACB ∶∠ADB=1∶2∶3,⊙O是△ABD的外接圆.
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图②),求∠CAD的度数.
21. 如图,已知平面直角坐标系中,A(0,4),B(4,4),C(6,2).
(1)写出经过A,B,C三点的圆弧所在圆的圆心M的坐标:(________,________);
(2)判断点D(5,-2)与⊙M的位置关系.
22. 在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
23. 如图,△ABC外切于⊙O,切点分别为D,E,F,∠A=60°,BC=7,⊙O的半径为.
(1)求BF+CE的值;
(2)求△ABC的周长.
24. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
人教版九年级上册 24.2 点和圆、直线和圆的位置关系 同步培优-答案
一、选择题
1. 【答案】D
2. 【答案】A
3. 【答案】B [解析] 若⊙P位于y轴左侧且与y轴相切,则平移的距离为1;若⊙P位于y轴右侧且与y轴相切,则平移的距离为5.
4. 【答案】C [解析] 因为所求直线到圆心O的距离为2.2 cm>半径2 cm,所以此直线与⊙O相离,所以这条直线为直线l3.
5. 【答案】D [解析] ∵AB为⊙O的切线,
∴∠OAB=90°.
∵∠ABO=36°,∴∠AOB=90°-∠ABO=54°.
∴∠ADC=∠AOB=27°.故选D.
6. 【答案】C [解析] 由题意可知,圆的半径为3 cm.∵圆心到直线l的距离为π cm>圆的半径3 cm,∴直线l与⊙O相离.故选C.
7. 【答案】C
8. 【答案】B
二、填空题
9. 【答案】219° [解析]连接AB,
∵PA,PB是☉O的切线,
∴PA=PB.
∵∠P=102°,
∴∠PAB=∠PBA=(180°-102°)=39°.
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°.
10. 【答案】2 [解析]直角三角形的斜边==13,所以它的内切圆半径==2.
11. 【答案】0≤d≤3
12. 【答案】相交 [解析] 设AB的中点为O,则点O到CD的距离为2.8.因为⊙O的半径为3,3>2.8,所以直线CD与⊙O的位置关系是相交.
13. 【答案】12 [解析] ∵PA,PB分别切⊙O于A,B两点,CD切⊙O于点E,∴PB=PA=6,CA=CE,DB=DE,∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=12.
14. 【答案】 【解析】如解图,连接EO并延长交AD于点F,连接OD、OA,则OD=OA.∵BC与⊙O相切于点E,∴OE⊥BC,∵四边形ABCD是矩形,∴AD∥BC,∴EF⊥AD,∴DF=AF=AD=6,在Rt△ODF中,设OD=r,则OF=EF-OE=AB-OE=8-r,在Rt△ODF中,由勾股定理得DF2+OF2=OD2,即62+(8-r)2=r2,解得r=.∴⊙O的半径为.
解图
15. 【答案】相交 [解析] ∵⊙M的圆心为M(-2,2),则⊙M关于y轴对称的⊙M′的圆心为M′(2,2).因为M′B=2>点M′到直线AB的距离,所以直线AB与⊙M′相交.
16. 【答案】1 cm或4 cm [解析] 若点P在⊙O内,如图①.∵AP=3 cm,BP=5 cm,
∴AB=8 cm,∴OA=4 cm;
若点P在⊙O外,如图②.
∵AP=3 cm,BP=5 cm,
∴AB=2 cm,
∴OA=1 cm.
三、解答题
17. 【答案】
证明:如图,连接OC,过点O作OD⊥PB于点D.
∵⊙O与PA相切于点C,
∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC,∴直线PB与⊙O相切.
18. 【答案】
解:(1)如图,过点B作BM⊥AC于点M,
则班车行驶了0.5小时的时候到达点M.
∵AM=60×0.5=30(千米),AB=50千米,
∴BM=40千米.
答:此时,班车到发射塔的距离是40千米.
(2)能.理由如下:如图,连接BC.
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC-AM=120-30=90(千米),
∴BC===10 (千米)<100千米,
∴到C城后还能接收到信号.
19. 【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
20. 【答案】
(1)证明:如解图,连接OA,OD.设∠ABC=x,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∴∠ADB=3x,∠ACB=2x,
解图
∴ ∠DAC=x,∠AOD=2∠ABC=2x,
∴∠OAD==90°-x,(2分)
∴∠OAC=90°-x+x=90°,
∴OA⊥AC,
又∵OA为⊙O的半径,
∴AC是⊙O的切线.(4分)
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∠ABC+∠ADB=90°,
∴∠ABC+3∠ABC=90°,(6分)
解得∠ABC=22.5°,
∴∠ADB=67.5°,∠ACB=45°,
∴∠CAD=∠ADB-∠ACB=22.5°.(8分)
21. 【答案】
解:(1)2 0
(2)∵⊙M的半径AM==2 ,
线段MD==<2 ,
∴点D在⊙M内.
22. 【答案】
解:⊙A与直线BC相交.
理由:过点A作AD⊥BC于点D,
则BD=CD=8.
∵AB=AC=10,
∴AD=6.
∵6<7,
∴⊙A与直线BC相交.
23. 【答案】
解:(1)∵△ABC外切于⊙O,切点分别为D,E,F,∴BF=BD,CE=CD,∴BF+CE=BD+CD=BC=7.故BF+CE的值是7.
(2)如图,连接OE,OA.∵△ABC外切于⊙O,切点分别为D,E,F,
∴AE=AF,∠OEA=90°,∠OAE=∠BAC=30°,
∴OA=2OE=2 .
由勾股定理,得AE===3,∴AF=3.
∴△ABC的周长是AB+BC+AC=AF+AE+CE+BF+BC=3+3+7+7=20.
24. 【答案】
解:(1)证明:如图,连接BD,OD,OE.
∵AB为半圆O的直径,
∴∠ADB=∠BDC=90°.
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE.
在△OBE和△ODE中,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,即OD⊥DE.
又∵OD是半圆O的半径,
∴DE是半圆O的切线.
(2)在Rt△ABC中,∠BAC=30°,
∴BC=AC.
∵BC=2DE=4,∴AC=8.
又∵∠C=90°-∠BAC=60°,DE=BE=EC,
∴△DEC为等边三角形,∴DC=DE=2,
∴AD=AC-DC=6.
一、选择题
1. 2019·益阳如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD
C.AB⊥PD D.AB平分PD
2. 已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )
A.1 B.2
C.3 D.4
3. 如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1 B.1或5 C.3 D.5
4. 平面上⊙O与四条直线l1,l2,l3,l4的位置关系如图.若⊙O的半径为2 cm,且点O到其中一条直线的距离为2.2 cm,则这条直线是( )
A.ll B.l2 C.l3 D.l4
5. 如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为( )
A.54° B.36° C.32° D.27°
6. 已知⊙O的面积为9π cm2,若点O到直线l的距离为π cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
7. 已知:在△ABC中,AB=AC,求证:∠B<90°.下面写出了用反证法证明这个命题过程中的四个推理步骤:①因为∠B+∠C≥180°与三角形内角和定理相矛盾;②所以∠B<90°;③假设∠B≥90°;④由AB=AC,得∠C=∠B≥90°,即∠B+∠C≥180°.这四个步骤正确的顺序应是( )
A.①②③④ B.③④②①
C.③④①② D.④③②①
8. 2020·武汉模拟 在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(-10,1)与⊙O的位置关系为( )
A.点P在⊙O上 B.点P在⊙O外
C.点P在⊙O内 D.无法确定
二、填空题
9. 如图,PA,PB是☉O的切线,A,B为切点,点C,D在☉O上.若∠P=102°,则∠A+∠C= .
10. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为 .
11. 设⊙O的半径为3,点O到直线l的距离为d,若直线l与⊙O至少有一个公共点,则d的取值范围是________.
12. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线CD与⊙O的位置关系是________.
13. 如图0,PA,PB分别切⊙O于点A,B,PA=6,CD切⊙O于点E,分别交PA,PB于C,D两点,则△PCD的周长是________.
14. 如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E.则⊙O的半径为________.
15. 如图,⊙M的圆心为M(-2,2),半径为2,直线AB过点A(0,-2),B(2,0),则⊙M关于y轴对称的⊙M′与直线AB的位置关系是________.
16. 已知点P到⊙O上的点的最短距离为3 cm,最长距离为5 cm,则⊙O的半径为__________.
三、解答题
17. 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.求证:直线PB与⊙O相切.
18. 如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能不能接收到信号,并说明理由.
图
19. 2018·邵阳 如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
20. 如图①,在△ABC中,点D在边BC上,∠ABC ∶∠ACB ∶∠ADB=1∶2∶3,⊙O是△ABD的外接圆.
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图②),求∠CAD的度数.
21. 如图,已知平面直角坐标系中,A(0,4),B(4,4),C(6,2).
(1)写出经过A,B,C三点的圆弧所在圆的圆心M的坐标:(________,________);
(2)判断点D(5,-2)与⊙M的位置关系.
22. 在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
23. 如图,△ABC外切于⊙O,切点分别为D,E,F,∠A=60°,BC=7,⊙O的半径为.
(1)求BF+CE的值;
(2)求△ABC的周长.
24. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
人教版九年级上册 24.2 点和圆、直线和圆的位置关系 同步培优-答案
一、选择题
1. 【答案】D
2. 【答案】A
3. 【答案】B [解析] 若⊙P位于y轴左侧且与y轴相切,则平移的距离为1;若⊙P位于y轴右侧且与y轴相切,则平移的距离为5.
4. 【答案】C [解析] 因为所求直线到圆心O的距离为2.2 cm>半径2 cm,所以此直线与⊙O相离,所以这条直线为直线l3.
5. 【答案】D [解析] ∵AB为⊙O的切线,
∴∠OAB=90°.
∵∠ABO=36°,∴∠AOB=90°-∠ABO=54°.
∴∠ADC=∠AOB=27°.故选D.
6. 【答案】C [解析] 由题意可知,圆的半径为3 cm.∵圆心到直线l的距离为π cm>圆的半径3 cm,∴直线l与⊙O相离.故选C.
7. 【答案】C
8. 【答案】B
二、填空题
9. 【答案】219° [解析]连接AB,
∵PA,PB是☉O的切线,
∴PA=PB.
∵∠P=102°,
∴∠PAB=∠PBA=(180°-102°)=39°.
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°.
10. 【答案】2 [解析]直角三角形的斜边==13,所以它的内切圆半径==2.
11. 【答案】0≤d≤3
12. 【答案】相交 [解析] 设AB的中点为O,则点O到CD的距离为2.8.因为⊙O的半径为3,3>2.8,所以直线CD与⊙O的位置关系是相交.
13. 【答案】12 [解析] ∵PA,PB分别切⊙O于A,B两点,CD切⊙O于点E,∴PB=PA=6,CA=CE,DB=DE,∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=12.
14. 【答案】 【解析】如解图,连接EO并延长交AD于点F,连接OD、OA,则OD=OA.∵BC与⊙O相切于点E,∴OE⊥BC,∵四边形ABCD是矩形,∴AD∥BC,∴EF⊥AD,∴DF=AF=AD=6,在Rt△ODF中,设OD=r,则OF=EF-OE=AB-OE=8-r,在Rt△ODF中,由勾股定理得DF2+OF2=OD2,即62+(8-r)2=r2,解得r=.∴⊙O的半径为.
解图
15. 【答案】相交 [解析] ∵⊙M的圆心为M(-2,2),则⊙M关于y轴对称的⊙M′的圆心为M′(2,2).因为M′B=2>点M′到直线AB的距离,所以直线AB与⊙M′相交.
16. 【答案】1 cm或4 cm [解析] 若点P在⊙O内,如图①.∵AP=3 cm,BP=5 cm,
∴AB=8 cm,∴OA=4 cm;
若点P在⊙O外,如图②.
∵AP=3 cm,BP=5 cm,
∴AB=2 cm,
∴OA=1 cm.
三、解答题
17. 【答案】
证明:如图,连接OC,过点O作OD⊥PB于点D.
∵⊙O与PA相切于点C,
∴OC⊥PA.
∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC,∴直线PB与⊙O相切.
18. 【答案】
解:(1)如图,过点B作BM⊥AC于点M,
则班车行驶了0.5小时的时候到达点M.
∵AM=60×0.5=30(千米),AB=50千米,
∴BM=40千米.
答:此时,班车到发射塔的距离是40千米.
(2)能.理由如下:如图,连接BC.
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC-AM=120-30=90(千米),
∴BC===10 (千米)<100千米,
∴到C城后还能接收到信号.
19. 【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
20. 【答案】
(1)证明:如解图,连接OA,OD.设∠ABC=x,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∴∠ADB=3x,∠ACB=2x,
解图
∴ ∠DAC=x,∠AOD=2∠ABC=2x,
∴∠OAD==90°-x,(2分)
∴∠OAC=90°-x+x=90°,
∴OA⊥AC,
又∵OA为⊙O的半径,
∴AC是⊙O的切线.(4分)
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∠ABC+∠ADB=90°,
∴∠ABC+3∠ABC=90°,(6分)
解得∠ABC=22.5°,
∴∠ADB=67.5°,∠ACB=45°,
∴∠CAD=∠ADB-∠ACB=22.5°.(8分)
21. 【答案】
解:(1)2 0
(2)∵⊙M的半径AM==2 ,
线段MD==<2 ,
∴点D在⊙M内.
22. 【答案】
解:⊙A与直线BC相交.
理由:过点A作AD⊥BC于点D,
则BD=CD=8.
∵AB=AC=10,
∴AD=6.
∵6<7,
∴⊙A与直线BC相交.
23. 【答案】
解:(1)∵△ABC外切于⊙O,切点分别为D,E,F,∴BF=BD,CE=CD,∴BF+CE=BD+CD=BC=7.故BF+CE的值是7.
(2)如图,连接OE,OA.∵△ABC外切于⊙O,切点分别为D,E,F,
∴AE=AF,∠OEA=90°,∠OAE=∠BAC=30°,
∴OA=2OE=2 .
由勾股定理,得AE===3,∴AF=3.
∴△ABC的周长是AB+BC+AC=AF+AE+CE+BF+BC=3+3+7+7=20.
24. 【答案】
解:(1)证明:如图,连接BD,OD,OE.
∵AB为半圆O的直径,
∴∠ADB=∠BDC=90°.
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE.
在△OBE和△ODE中,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,即OD⊥DE.
又∵OD是半圆O的半径,
∴DE是半圆O的切线.
(2)在Rt△ABC中,∠BAC=30°,
∴BC=AC.
∵BC=2DE=4,∴AC=8.
又∵∠C=90°-∠BAC=60°,DE=BE=EC,
∴△DEC为等边三角形,∴DC=DE=2,
∴AD=AC-DC=6.
同课章节目录
