2021--2022学年人教版九年级数学上册24.3 正多边形和圆 同步培优(Word版含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册24.3 正多边形和圆 同步培优(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 693.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 22:06:44 | ||
图片预览




文档简介
人教版九年级上册 24.3 正多边形和圆 同步培优
一、选择题
1. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
2. (2019 贵阳)如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是
A.30° B.45°
C.60° D.90°
3. 2019·安徽月考 如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
A.AE∥BF B.AF∥CD
C.DF=AF D.AB=BF
4. 正方形ABCD与正八边形EFGHKLMN的边长相等,初始位置如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合……按这样的方式将正方形ABCD旋转2020次后,正方形ABCD中与正八边形EFGHKLMN的边重合的边是( )
A.AB B.BC C.CD D.DA
5. 如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的圆O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆O上时,点C转过的度数为( )
A.12° B.16° C.20° D.24°
6. 如图,将两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张纸片保持不动,将上面一张纸片沿水平方向向左平移a个单位长度,则空白部分与阴影部分的面积之比是( )
A.5∶2 B.3∶2 C.3∶1 D.2∶1
7. 如图0,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:1.以点D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;
2.连接AB,BC,AC.△ABC即为所求作的三角形.
乙:1.作OD的中垂线,交⊙O于B,C两点;
2.连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
8. 已知正六边形的半径为r,则它的边长、边心距、面积分别为( )
A.r,r,r2 B.r,,2r2
C.r,r,r2 D.r,,r2
二、填空题
9. 一个圆内接正六边形的边长为2,那么这个正六边形的边心距为________.
10. 如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为________cm.
11. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸带宽为________.
12. 如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则所对的圆心角∠BOD的大小为________度.
13. 如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=________°.
14. (2019 海南)如图,与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角的大小为__________度.
15. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=________°.
16. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
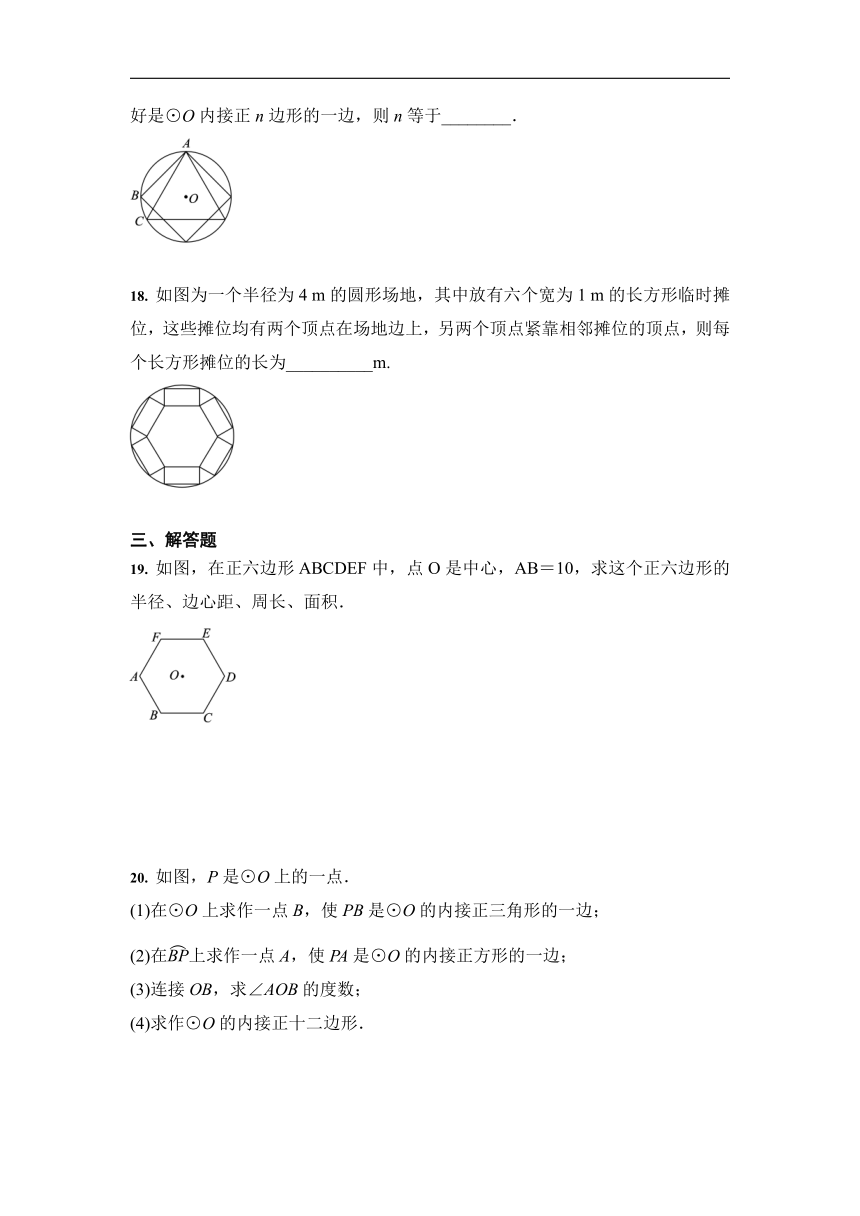
17. 如图,AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.
18. 如图为一个半径为4 m的圆形场地,其中放有六个宽为1 m的长方形临时摊位,这些摊位均有两个顶点在场地边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为__________m.
三、解答题
19. 如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.
20. 如图,P是⊙O上的一点.
(1)在⊙O上求作一点B,使PB是⊙O的内接正三角形的一边;
(2)在上求作一点A,使PA是⊙O的内接正方形的一边;
(3)连接OB,求∠AOB的度数;
(4)求作⊙O的内接正十二边形.
21. 如图,A,B,C,D,E是⊙O上的五等分点,连接AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)计算∠CAD的度数;
(2)连接AE,求证:AE=ME.
22. 如图2,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1) 求图①中∠MON的度数;
(2) 图②中∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
人教版九年级上册 24.3 正多边形和圆 同步培优-答案
一、选择题
1. 【答案】A [解析] ∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
故选A.
2. 【答案】A
【解析】∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,
∴∠CBD=(180°-120°)=30°,故选A.
3. 【答案】C
4. 【答案】A [解析] 由题意可得正方形每旋转8次则回到原来的位置.
∵2020÷8=252……4,
∴正方形ABCD旋转2020次后,AB与正八边形EFGHKLMN的边重合.
5. 【答案】A [解析] 设点E第一次落在圆上时的对应点为E′,连接OA,OB,OE′,如图.
∵五边形ABCDE为正五边形,
∴∠EAB=108°.
∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在圆O上的点E′处,
∴AE′=AE=3.
∵OA=AB=OB=OE′=3,
∴△OAE′,△OAB都为等边三角形,
∴∠OAB=∠OAE′=60°,
∴∠E′AB=120°,
∴∠EAE′=12°,
∴当点E第一次落在圆O上时,点C转过的度数为12°.
6. 【答案】C [解析] 正六边形的面积=6××(2a)2=6 a2,阴影部分的面积=a·2 a=2 a2,
∴空白部分与阴影部分的面积之比是=6 a2∶2 a2=3∶1.
7. 【答案】C [解析] 由甲的作法可知连接OB,BD,OC,CD后,OB=BD=OD=OC=CD,所以△BOD和△COD都是等边三角形,四边形OBDC是菱形,所以∠BOC=120°,则∠BAC=60°.因为四边形OBDC是菱形,所以AD⊥BC,AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以他的作法是正确的.由乙的作法可知∠BOC=120°,所以∠BAC=60°.又因为AD⊥BC,所以AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以他的作法是正确的.故选C.
8. 【答案】D
二、填空题
9. 【答案】
10. 【答案】25 【解析】 如解图,取圆心为O,连接OA、OC,OC交AB于点D,则OC⊥AB.设⊙O 的半径为r,则OA=OC=r,又∵CD=10,∴OD=r-10,∵AB=40,OC⊥AB,∴AD=20.在Rt△ADO中,由勾股定理得:r2=202+(r-10)2,解得r=25,即脸盆的半径为25 cm.
11. 【答案】 [解析] 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度为.
12. 【答案】144 [解析] ∵⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,∴OB⊥AB,OD⊥DE.∵正五边形每个内角均为108°,
∴∠BOD=∠C+∠OBC+∠ODC=108°×3-90°×2=144°.
13. 【答案】125 【解析】∵⊙O是△ABC的内切圆,∴OB、OC分别是∠ABC、∠ACB的平分线,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(70°+40°)=55°.∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
14. 【答案】144
【解析】五边形ABCDE是正五边形,∴.
∵AB、DE与相切,∴,
∴,故答案为:144.
15. 【答案】48 [解析] 连接AO,则有∠AOM=×360°=120°,∠AOB=×360°=72°,
∴∠BOM=∠AOM-∠AOB=120°-72°=48°.
16. 【答案】8+8 [解析] 易证四边形ABCD是正方形.
由题意可得AD=2+×2=2+2 ,
∴四边形ABCD的周长是4×(2+2 )=8+8 .
故答案为8+8 .
17. 【答案】12 [解析] 连接OA,OB,OC,如图.
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOB=90°,∠AOC=120°,
∴∠BOC=∠AOC-∠AOB=30°,∴n==12,即BC恰好是⊙O内接正十二边形的一边.
18. 【答案】 [解析] 设圆心是O,连接OA,OB,过点O作OC⊥BC于点C,交AD于点D.设长方形摊位的长是2x m.在Rt△OAD中,∠AOD=30°,AD=x m,则OD=x m.
在Rt△OBC中,由勾股定理,得OC= m.
∵OC-OD=CD=1 m,
∴=x+1,
解得x=(负值已舍去),
则2x=,
∴长方形摊位的长为 m.
三、解答题
19. 【答案】
解:连接OB,OC,过点O作OH⊥BC于点H.∵正六边形的中心角为=60°,OB=OC,∴△OBC是等边三角形,
∴半径R=OB=BC=AB=10.∵OH⊥BC,∴∠BOH=30°,∴BH=OB=5.
在Rt△OBH中,边心距r=OH==5 ,周长l=6AB=6×10=60.
∵S△OBC=BC·OH=×10×5 =25 ,
∴正六边形的面积S=6S△OBC=6×25 =150 .
20. 【答案】
解:(1)如图①,以点P为圆心,OP长为半径画圆弧交⊙O于点M,再以点M为圆心,OM长为半径画圆弧交⊙O于点B,连接PB,则PB即为所求.
(2)如图①,作直径PH,再过圆心作直径PH的垂线交于点A,连接PA,则PA即为所求.
(3)∵PA是⊙O的内接正方形的一边,
∴∠AOP=90°.
∵PB是⊙O的内接正三角形的一边,
∴∠BOP=120°,∴∠AOB=30°.
(4)如图②,以点P为圆心,OP长为半径在⊙O上依次截取5个点,这5个点连同点P是⊙O的六等分点,再作各弧的中点,顺次连接12个点,得到⊙O的内接正十二边形.
21. 【答案】
解:(1)∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD==72°,
∴∠CAD=∠COD=36°.
(2)证明:∵A,B,C,D,E是⊙O上的五等分点,∴====,
∴∠DAE=∠AEB=∠CAD=36°,
∴∠MAE=72°,
∴∠AME=180°-∠MAE-∠AEB=72°=∠MAE,∴AE=ME.
22. 【答案】
解:(1)方法一:连接OB,OC.
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
方法二:连接OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.
∵BM=CN,∴AM=BN.
又∵OA=OB,∴△AOM≌△BON,
∴∠AOM=∠BON,∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=°.
一、选择题
1. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
2. (2019 贵阳)如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是
A.30° B.45°
C.60° D.90°
3. 2019·安徽月考 如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
A.AE∥BF B.AF∥CD
C.DF=AF D.AB=BF
4. 正方形ABCD与正八边形EFGHKLMN的边长相等,初始位置如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合……按这样的方式将正方形ABCD旋转2020次后,正方形ABCD中与正八边形EFGHKLMN的边重合的边是( )
A.AB B.BC C.CD D.DA
5. 如图,边长为3的正五边形ABCDE的顶点A,B在半径为3的圆O上,其他各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆O上时,点C转过的度数为( )
A.12° B.16° C.20° D.24°
6. 如图,将两张完全相同的正六边形纸片(边长为2a)重合在一起,下面一张纸片保持不动,将上面一张纸片沿水平方向向左平移a个单位长度,则空白部分与阴影部分的面积之比是( )
A.5∶2 B.3∶2 C.3∶1 D.2∶1
7. 如图0,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:1.以点D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;
2.连接AB,BC,AC.△ABC即为所求作的三角形.
乙:1.作OD的中垂线,交⊙O于B,C两点;
2.连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
8. 已知正六边形的半径为r,则它的边长、边心距、面积分别为( )
A.r,r,r2 B.r,,2r2
C.r,r,r2 D.r,,r2
二、填空题
9. 一个圆内接正六边形的边长为2,那么这个正六边形的边心距为________.
10. 如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10 cm,则该脸盆的半径为________cm.
11. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸带宽为________.
12. 如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则所对的圆心角∠BOD的大小为________度.
13. 如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=________°.
14. (2019 海南)如图,与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角的大小为__________度.
15. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=________°.
16. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
17. 如图,AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,而BC恰好是⊙O内接正n边形的一边,则n等于________.
18. 如图为一个半径为4 m的圆形场地,其中放有六个宽为1 m的长方形临时摊位,这些摊位均有两个顶点在场地边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为__________m.
三、解答题
19. 如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.
20. 如图,P是⊙O上的一点.
(1)在⊙O上求作一点B,使PB是⊙O的内接正三角形的一边;
(2)在上求作一点A,使PA是⊙O的内接正方形的一边;
(3)连接OB,求∠AOB的度数;
(4)求作⊙O的内接正十二边形.
21. 如图,A,B,C,D,E是⊙O上的五等分点,连接AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)计算∠CAD的度数;
(2)连接AE,求证:AE=ME.
22. 如图2,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1) 求图①中∠MON的度数;
(2) 图②中∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
人教版九年级上册 24.3 正多边形和圆 同步培优-答案
一、选择题
1. 【答案】A [解析] ∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
故选A.
2. 【答案】A
【解析】∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,
∴∠CBD=(180°-120°)=30°,故选A.
3. 【答案】C
4. 【答案】A [解析] 由题意可得正方形每旋转8次则回到原来的位置.
∵2020÷8=252……4,
∴正方形ABCD旋转2020次后,AB与正八边形EFGHKLMN的边重合.
5. 【答案】A [解析] 设点E第一次落在圆上时的对应点为E′,连接OA,OB,OE′,如图.
∵五边形ABCDE为正五边形,
∴∠EAB=108°.
∵正五边形ABCDE绕点A逆时针旋转,点E第一次落在圆O上的点E′处,
∴AE′=AE=3.
∵OA=AB=OB=OE′=3,
∴△OAE′,△OAB都为等边三角形,
∴∠OAB=∠OAE′=60°,
∴∠E′AB=120°,
∴∠EAE′=12°,
∴当点E第一次落在圆O上时,点C转过的度数为12°.
6. 【答案】C [解析] 正六边形的面积=6××(2a)2=6 a2,阴影部分的面积=a·2 a=2 a2,
∴空白部分与阴影部分的面积之比是=6 a2∶2 a2=3∶1.
7. 【答案】C [解析] 由甲的作法可知连接OB,BD,OC,CD后,OB=BD=OD=OC=CD,所以△BOD和△COD都是等边三角形,四边形OBDC是菱形,所以∠BOC=120°,则∠BAC=60°.因为四边形OBDC是菱形,所以AD⊥BC,AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以他的作法是正确的.由乙的作法可知∠BOC=120°,所以∠BAC=60°.又因为AD⊥BC,所以AD平分BC,所以AB=AC,所以△ABC是等边三角形,所以他的作法是正确的.故选C.
8. 【答案】D
二、填空题
9. 【答案】
10. 【答案】25 【解析】 如解图,取圆心为O,连接OA、OC,OC交AB于点D,则OC⊥AB.设⊙O 的半径为r,则OA=OC=r,又∵CD=10,∴OD=r-10,∵AB=40,OC⊥AB,∴AD=20.在Rt△ADO中,由勾股定理得:r2=202+(r-10)2,解得r=25,即脸盆的半径为25 cm.
11. 【答案】 [解析] 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度为.
12. 【答案】144 [解析] ∵⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,∴OB⊥AB,OD⊥DE.∵正五边形每个内角均为108°,
∴∠BOD=∠C+∠OBC+∠ODC=108°×3-90°×2=144°.
13. 【答案】125 【解析】∵⊙O是△ABC的内切圆,∴OB、OC分别是∠ABC、∠ACB的平分线,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(70°+40°)=55°.∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
14. 【答案】144
【解析】五边形ABCDE是正五边形,∴.
∵AB、DE与相切,∴,
∴,故答案为:144.
15. 【答案】48 [解析] 连接AO,则有∠AOM=×360°=120°,∠AOB=×360°=72°,
∴∠BOM=∠AOM-∠AOB=120°-72°=48°.
16. 【答案】8+8 [解析] 易证四边形ABCD是正方形.
由题意可得AD=2+×2=2+2 ,
∴四边形ABCD的周长是4×(2+2 )=8+8 .
故答案为8+8 .
17. 【答案】12 [解析] 连接OA,OB,OC,如图.
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOB=90°,∠AOC=120°,
∴∠BOC=∠AOC-∠AOB=30°,∴n==12,即BC恰好是⊙O内接正十二边形的一边.
18. 【答案】 [解析] 设圆心是O,连接OA,OB,过点O作OC⊥BC于点C,交AD于点D.设长方形摊位的长是2x m.在Rt△OAD中,∠AOD=30°,AD=x m,则OD=x m.
在Rt△OBC中,由勾股定理,得OC= m.
∵OC-OD=CD=1 m,
∴=x+1,
解得x=(负值已舍去),
则2x=,
∴长方形摊位的长为 m.
三、解答题
19. 【答案】
解:连接OB,OC,过点O作OH⊥BC于点H.∵正六边形的中心角为=60°,OB=OC,∴△OBC是等边三角形,
∴半径R=OB=BC=AB=10.∵OH⊥BC,∴∠BOH=30°,∴BH=OB=5.
在Rt△OBH中,边心距r=OH==5 ,周长l=6AB=6×10=60.
∵S△OBC=BC·OH=×10×5 =25 ,
∴正六边形的面积S=6S△OBC=6×25 =150 .
20. 【答案】
解:(1)如图①,以点P为圆心,OP长为半径画圆弧交⊙O于点M,再以点M为圆心,OM长为半径画圆弧交⊙O于点B,连接PB,则PB即为所求.
(2)如图①,作直径PH,再过圆心作直径PH的垂线交于点A,连接PA,则PA即为所求.
(3)∵PA是⊙O的内接正方形的一边,
∴∠AOP=90°.
∵PB是⊙O的内接正三角形的一边,
∴∠BOP=120°,∴∠AOB=30°.
(4)如图②,以点P为圆心,OP长为半径在⊙O上依次截取5个点,这5个点连同点P是⊙O的六等分点,再作各弧的中点,顺次连接12个点,得到⊙O的内接正十二边形.
21. 【答案】
解:(1)∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD==72°,
∴∠CAD=∠COD=36°.
(2)证明:∵A,B,C,D,E是⊙O上的五等分点,∴====,
∴∠DAE=∠AEB=∠CAD=36°,
∴∠MAE=72°,
∴∠AME=180°-∠MAE-∠AEB=72°=∠MAE,∴AE=ME.
22. 【答案】
解:(1)方法一:连接OB,OC.
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
方法二:连接OA,OB.
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.
∵BM=CN,∴AM=BN.
又∵OA=OB,∴△AOM≌△BON,
∴∠AOM=∠BON,∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=°.
同课章节目录
