2021-2022七年级下册第五章 生活中的轴对称轴对称图形3—角平分线 课件(共24张PPT)
文档属性
| 名称 | 2021-2022七年级下册第五章 生活中的轴对称轴对称图形3—角平分线 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 39.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 11:02:38 | ||
图片预览





文档简介
(共24张PPT)
北师版七年级下册数学
3 简单的轴对称图形
第五章 生活中的轴对称
角平分线的性质
1.通过验证等方式,探究并掌握角平分线的性质定理。(重点)
2.能用尺规作图作已知角的角平分线。
3.能运用角的平分线性质解决简单的几何问题。(难点)
学习目标
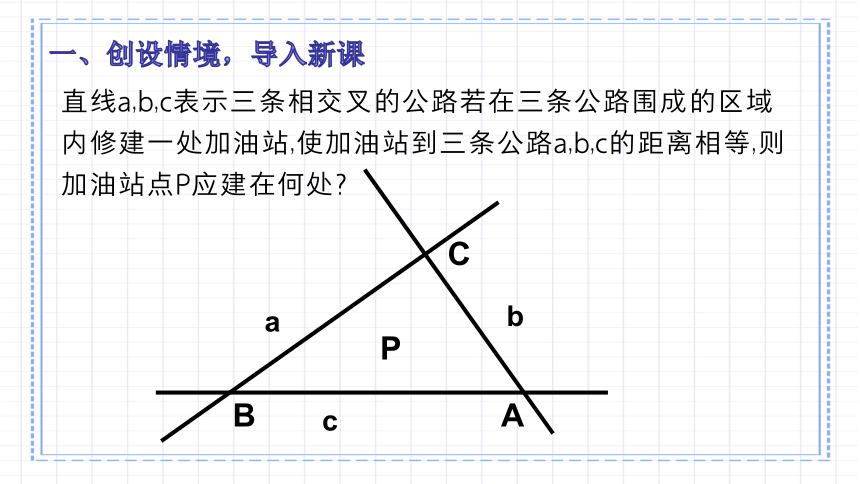
直线a,b,c表示三条相交叉的公路若在三条公路围成的区域内修建一处加油站,使加油站到三条公路a,b,c的距离相等,则加油站点P应建在何处?
a
b
c
A
B
C
一、创设情境,导入新课
P
二、探究新知1
问题1:请在纸上画一个角并剪下这个角,然后将其对折,你会发现什么?
这个角是一个轴对称图形,折痕所在的直线就是这个角的对称轴 。
C
结论:
角是轴对称图形
对称轴是角平分线所在的直线
A
B
O
二、探究新知1
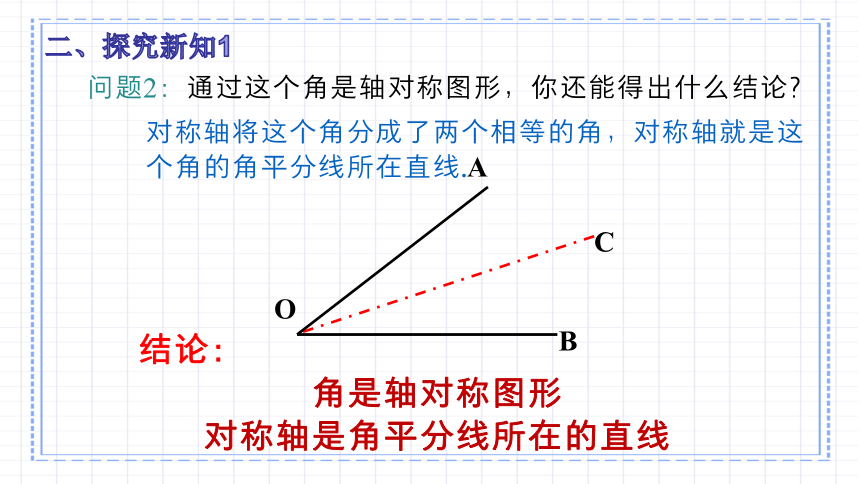
问题2:通过这个角是轴对称图形,你还能得出什么结论?
对称轴将这个角分成了两个相等的角,对称轴就是这个角的角平分线所在直线.
问题3:如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?
二、探究新知1
不能,
如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线。
A
B
C
(E)
D
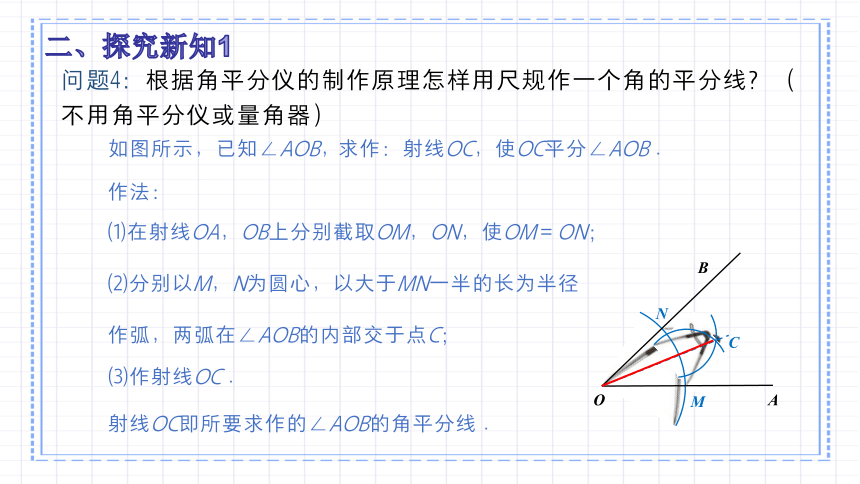
(1)在射线OA,OB上分别截取OM,ON,使OM=ON;
(2)分别以M,N为圆心,以大于MN一半的长为半径
作弧,两弧在∠AOB的内部交于点C;
(3)作射线OC .
射线OC即所要求作的∠AOB的角平分线 .
如图所示,已知∠AOB,
求作:射线OC,使OC平分∠AOB .
作法:
A
O
B
M
N
C
二、探究新知1
问题4:根据角平分仪的制作原理怎样用尺规作一个角的平分线?(不用角平分仪或量角器)
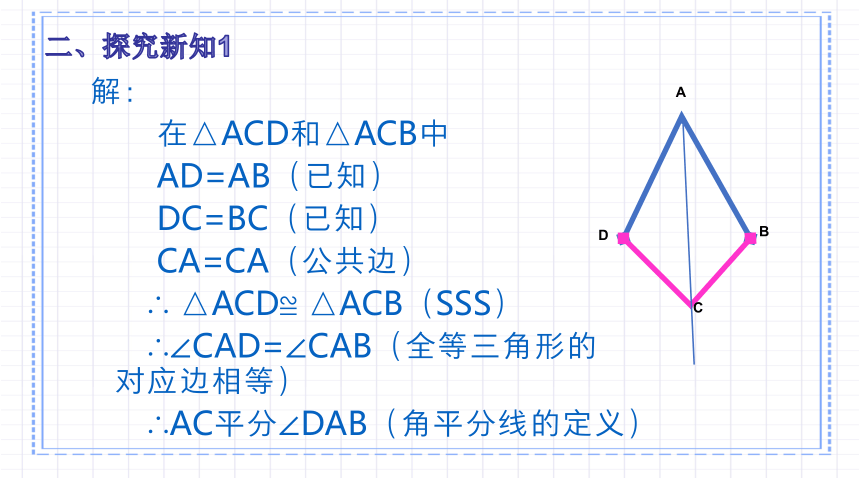
解:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
二、探究新知1
1.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.角平分线上的点到角两边的距离相等
C.AAS D. ASA
A
B
M
N
C
O
A
二、探究新知1
练习
二、探究新知2
在∠AOB的平分线上任意找一个点P,过P分别向OA、OB画垂线段PD、PE
观察并猜测PD与PE的长
有什么关系?你能验证吗?
D
P
E
A
O
B
C
角的平分线上的点到这个角的两边的距离相等。
验证猜想
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
试说明:PD=PE.
P
A
O
B
C
D
E
解:
∵ PD⊥OA,PE⊥OB,(已知)
∴ ∠PDO= ∠PEO=90 °(垂直的定义).
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.(全等三角形的对应边相等)
角的平分线上的点到角的两边的距离相等
二、探究新知2
角平分线的性质
B
A
D
O
P
E
C
性质应用所具备的条件:
性质的作用:
证明线段相等。
(1)角的平分线;
(2)点在角平分线上;
(3)垂直距离。
角的平分线上的点到角的两边的距离相等
二、探究新知2
C
D
E
O
A
B
几何表达:
∵OC平分∠ AOB,
CD⊥OB, CE⊥OA
∴CD=CE
二、探究新知2
角平分线的性质
角的平分线上的点到角的两边的距离相等
推理的理由有三个,必须写完全,不能少了任何一个.
(1)∵ 如图,AD平分∠BAC(已知)
∴ = ,(在角的平分线上的点到这个角的两边的距离相等。)
BD CD
(×)
判断
二、探究新知2
(2)∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
二、探究新知2
(2)∵ 如图, DC⊥AC,DB⊥AB (已知)
BD CD
(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
BD
CD
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
二、探究新知2
例1 如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D,E,PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段———直接应用
三、典例精析
A
B
C
P
例2:如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P. 若PC=4, AB=14. (1)点P到AB的距离为_______;
D
4
温馨提示:存在一条垂线段———构造应用
三、典例精析
A
B
C
P
变式:如图,在Rt △ABC中,AC=BC,∠C=900,AP平分∠BAC交BC于点P,若PC=4,AB=14.
(2)求△APB的面积.
D
(3)求 PDB的周长.
·AB·PD=28.
由垂直平分线的性质,可知,PD=PC=4,
=
三、典例精析
例3:如图,已知AD∥BC,P是∠BAD与 ∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间
的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.
三、典例精析
1.应用角平分线性质:
存在角平分线
涉及距离问题
2.联系角平分线性质:
面积
周长
条件
知识与方法
利用角平分线的性质所得到的等量关系进行转化求解
a
b
c
A
B
P
D
E
F
C
四、学以致用,服务生活
直线a,b,c表示三条相交叉的公路若在三条公路围成的区域内修建一处加油站,使加油站到三条公路a,b,c的距离相等,则加油站点P应建在何处?
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
两距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
五、课堂小结
谢谢聆听
北师版七年级下册数学
3 简单的轴对称图形
第五章 生活中的轴对称
角平分线的性质
1.通过验证等方式,探究并掌握角平分线的性质定理。(重点)
2.能用尺规作图作已知角的角平分线。
3.能运用角的平分线性质解决简单的几何问题。(难点)
学习目标
直线a,b,c表示三条相交叉的公路若在三条公路围成的区域内修建一处加油站,使加油站到三条公路a,b,c的距离相等,则加油站点P应建在何处?
a
b
c
A
B
C
一、创设情境,导入新课
P
二、探究新知1
问题1:请在纸上画一个角并剪下这个角,然后将其对折,你会发现什么?
这个角是一个轴对称图形,折痕所在的直线就是这个角的对称轴 。
C
结论:
角是轴对称图形
对称轴是角平分线所在的直线
A
B
O
二、探究新知1
问题2:通过这个角是轴对称图形,你还能得出什么结论?
对称轴将这个角分成了两个相等的角,对称轴就是这个角的角平分线所在直线.
问题3:如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?
二、探究新知1
不能,
如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线。
A
B
C
(E)
D
(1)在射线OA,OB上分别截取OM,ON,使OM=ON;
(2)分别以M,N为圆心,以大于MN一半的长为半径
作弧,两弧在∠AOB的内部交于点C;
(3)作射线OC .
射线OC即所要求作的∠AOB的角平分线 .
如图所示,已知∠AOB,
求作:射线OC,使OC平分∠AOB .
作法:
A
O
B
M
N
C
二、探究新知1
问题4:根据角平分仪的制作原理怎样用尺规作一个角的平分线?(不用角平分仪或量角器)
解:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的 对应边相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
二、探究新知1
1.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.角平分线上的点到角两边的距离相等
C.AAS D. ASA
A
B
M
N
C
O
A
二、探究新知1
练习
二、探究新知2
在∠AOB的平分线上任意找一个点P,过P分别向OA、OB画垂线段PD、PE
观察并猜测PD与PE的长
有什么关系?你能验证吗?
D
P
E
A
O
B
C
角的平分线上的点到这个角的两边的距离相等。
验证猜想
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
试说明:PD=PE.
P
A
O
B
C
D
E
解:
∵ PD⊥OA,PE⊥OB,(已知)
∴ ∠PDO= ∠PEO=90 °(垂直的定义).
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.(全等三角形的对应边相等)
角的平分线上的点到角的两边的距离相等
二、探究新知2
角平分线的性质
B
A
D
O
P
E
C
性质应用所具备的条件:
性质的作用:
证明线段相等。
(1)角的平分线;
(2)点在角平分线上;
(3)垂直距离。
角的平分线上的点到角的两边的距离相等
二、探究新知2
C
D
E
O
A
B
几何表达:
∵OC平分∠ AOB,
CD⊥OB, CE⊥OA
∴CD=CE
二、探究新知2
角平分线的性质
角的平分线上的点到角的两边的距离相等
推理的理由有三个,必须写完全,不能少了任何一个.
(1)∵ 如图,AD平分∠BAC(已知)
∴ = ,(在角的平分线上的点到这个角的两边的距离相等。)
BD CD
(×)
判断
二、探究新知2
(2)∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
二、探究新知2
(2)∵ 如图, DC⊥AC,DB⊥AB (已知)
BD CD
(3)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
BD
CD
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
二、探究新知2
例1 如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D,E,PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段———直接应用
三、典例精析
A
B
C
P
例2:如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P. 若PC=4, AB=14. (1)点P到AB的距离为_______;
D
4
温馨提示:存在一条垂线段———构造应用
三、典例精析
A
B
C
P
变式:如图,在Rt △ABC中,AC=BC,∠C=900,AP平分∠BAC交BC于点P,若PC=4,AB=14.
(2)求△APB的面积.
D
(3)求 PDB的周长.
·AB·PD=28.
由垂直平分线的性质,可知,PD=PC=4,
=
三、典例精析
例3:如图,已知AD∥BC,P是∠BAD与 ∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间
的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.
三、典例精析
1.应用角平分线性质:
存在角平分线
涉及距离问题
2.联系角平分线性质:
面积
周长
条件
知识与方法
利用角平分线的性质所得到的等量关系进行转化求解
a
b
c
A
B
P
D
E
F
C
四、学以致用,服务生活
直线a,b,c表示三条相交叉的公路若在三条公路围成的区域内修建一处加油站,使加油站到三条公路a,b,c的距离相等,则加油站点P应建在何处?
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
两距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
五、课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
