2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.1等差数列的概念(第一课时) 课件(共20张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.1等差数列的概念(第一课时) 课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 12:12:22 | ||
图片预览








文档简介
(共20张PPT)
等差数列的概念
情境引入
我国有用12生肖纪年的习惯,例如:2021年是牛年,从2021年开始,牛年的年份为2021,2033,2045,2057,2069,2081....;这些年份有什么特点?
情境引入
圜丘坛为雕砌的三层露天圆台,坛面为艾叶青石,汉白玉栏板、栏柱雕成,两道外方里圆的围墙象征着"天圆地方"。由于是祭天坛,圜丘的整个结构是对数学的巧妙运用,坛面、台阶、栏杆的石制构件,都取九或九的倍数,即阳数,用以象征天。坛中心的圆形石板,叫天心石(亿兆景从石),站在上面高喊或发出敲击声,周围即起回音,自己听起来声音很大,好似一呼百应。
新知探究
1. 围绕天心石的9圈扇环形石板,从内到外各圈的石板数依次为
9,18,27,36,45,54,63,72,81. ①
我们常通过运算来发现规律。你能通过运算发现数列①的取值规律吗?
对于①,我们发现
18=9+9,27=18+9....81=72+9,
换一种写法,就是
18-9=9,27-18=9....81-72=9.
如果用{an}表示数列①,
那么有a2-a1=9,a3- a2 =9,...a9-a8=9.
这表明,数列①有这样的取值规律:从第2项起,每一项与它的前一项的差都等于同一个常数。
新知探究
2.S,M,L,XL,XXL,XXXL型号的女装上衣对应的尺码分别是
38,40,42,44,46,48.②
3.测量某地垂直地面方向上海拔500m以下的大气温度,得到从距离地面20m起每升高100m处的大气温度(单位:℃)依次为
25,24,23,22,21. ③
4.某人向银行贷款a万元,贷款时间为n年.如果个人贷款月利率为r,那么按照等额本金方式还款,他从某月开始,每月应还本金b(=12n)元,每月支付给银行的利息(单位:元)依次为
ar,ar-br,ar-2br,ar-3br,... ④
数列②-④是否也有这样的取值规律
新知探究
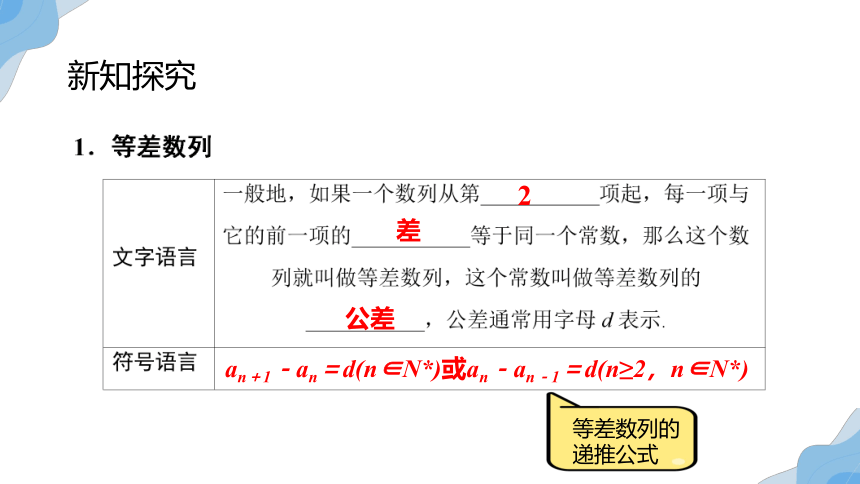
2
差
公差
an+1-an=d(n∈N*)或an-an-1=d(n≥2,n∈N*)
等差数列的递推公式
新知探究
练习1 判断下列数列是否为等差数列,若是,求出首项和公差
(1) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10
(2) 3,3,3,3,3,3
(3) 3x,6x,9x,12x,15x
(4)95,82,69,56,43,30
(5) 1,1.1,1.11,1.111,1.1111
(6) 1,-2,3,-4,5,-6
a1=3,公差 d=0 常数列
a1=3x 公差 d= 3x
×
a1=95 公差 d=-13
×
×
新知探究
练习2 判断题
(1)数列a,2a,3a,4a,…是等差数列 ( )
(2)数列a-2,2a-3,3a-4,4a-5,…是等差数列( )
(3)若an-an+1=3 (n∈N*),则{an}是公差为3的等差数列( )
(4)若a2-a1=a3-a2, 则数列{an}是等差数列( )
若an-an-1=an+1-an (n≥2,n∈N*),则数列{an}是等差数列( )
若an-an-1=an+2-an+1 (n≥2,n∈N*),则数列{an}是等差数列( )
1,2,5,6,9,10,…
新知探究
练习3 在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2 ,( ) , 4
(2)-12,( ) ,0
(3)a,( ),b
3
-6
新知探究
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列,这时A叫做a与b的等差中项。
2. 等差中项
由等差数列的定义可知
… …
新知探究
求等差数列1,4,7,10,13,16,…的通项公式
新知探究
如果一个数列a1,a2,a3,...,an,...是等差数列,它的公差是d,求这个数列通项公式?
解:
n=1时亦适合
迭代法
新知探究
如果一个数列a1,a2,a3,...,an,...是等差数列,它的公差是d,求这个数列通项公式?
解:
a2-a1=d
a3-a2=d
a4-a3=d
…
an-an-1=d (n ≥ 2)
累加以上n-1个式子得
an-a1=(n-1)d
又∵当n=1时,上式也成立
∴an=a1+(n-1)d
累加法
首项a1公差d的等差数列{an}的通项公式为
练习4 求下列等差数列的通项公式
(1)9,18,27,36,45,54,63,72...
(2)38,40,42,44,46,48...
(3)25,24,23,22,21.
(1)an=9+(n-1)×9=9n
(2)an=38+(n-1)×2=2n+36
(3)an=25+(n-1)×(-1)=-n+26
等差数列的通项公式的一般形式:an=am+(n-m)d
3. 等差数列的通项公式
a1 、an、n、d知三求一
新知探究
课堂巩固
例1.(1)已知等差数列{an}的通项公式为an =5-2n,
求{an}公差和首项;
(2)求等差数列8,5,2....的第20项
分析:(2)可以先根据数列的两个已知项求出通项公式,再利用通项公式求数列的第20项
解:(2)由已知条件,得d=5-8=-3.
把a1=8,d=-3代入an=a1+(n-1)d,
得an=8-3(n-1)=11-3n.
把n=20代入上式,得a20=11-3×20=-49.
所以,这个数列的第20项是-49.
课堂巩固
例2.-401是不是等差数列 -5,-9,-13,…,的项?如果是,是第几项?
分析:先求出数列的通项公式,它是一个关于n的方程,再看-401是否能使这个方程有正整数解.
解:由a1=-5,d=-9-(-5)=-4,
所以数列的通项公式为an=-5-4(n-1)=-4n-1.
令-4n-1=-401,解得n=100.
所以,-401是这个数列的项,是第100项。
课堂巩固
在等差数列中,已知a5=10,a12=31,求首项与公差.
解:设数列的首项为a1与公差为d
由题意可知
即这个等差数列的首项是-2,公差是3.
归纳:在等差数列{an}的通项公式中a1、d、an、n,知三求二
课堂巩固
P15课本练习4 已知在等差数列中,a4+a8=20,a7=12,求a4.
解:设数列的首项为a1与公差为d
由题意可知
∴这个等差数列的通项公式为an=0+(n-1)×2=2n-2
则a4=2×4-2=6
解得
课堂小结
从第2项起,每一项与它的前一项的差等于同一个常数
等差数列的定义
由三个数a,A,b组成的等差数列,A叫做a与b的等差中项。
等差中项
首项a1公差d,的等差数列{an}的通项公式为
通项公式
迭代法、累加法
通项公式的推导方法
P15 课本 练习 3、5
课后作业
等差数列的概念
情境引入
我国有用12生肖纪年的习惯,例如:2021年是牛年,从2021年开始,牛年的年份为2021,2033,2045,2057,2069,2081....;这些年份有什么特点?
情境引入
圜丘坛为雕砌的三层露天圆台,坛面为艾叶青石,汉白玉栏板、栏柱雕成,两道外方里圆的围墙象征着"天圆地方"。由于是祭天坛,圜丘的整个结构是对数学的巧妙运用,坛面、台阶、栏杆的石制构件,都取九或九的倍数,即阳数,用以象征天。坛中心的圆形石板,叫天心石(亿兆景从石),站在上面高喊或发出敲击声,周围即起回音,自己听起来声音很大,好似一呼百应。
新知探究
1. 围绕天心石的9圈扇环形石板,从内到外各圈的石板数依次为
9,18,27,36,45,54,63,72,81. ①
我们常通过运算来发现规律。你能通过运算发现数列①的取值规律吗?
对于①,我们发现
18=9+9,27=18+9....81=72+9,
换一种写法,就是
18-9=9,27-18=9....81-72=9.
如果用{an}表示数列①,
那么有a2-a1=9,a3- a2 =9,...a9-a8=9.
这表明,数列①有这样的取值规律:从第2项起,每一项与它的前一项的差都等于同一个常数。
新知探究
2.S,M,L,XL,XXL,XXXL型号的女装上衣对应的尺码分别是
38,40,42,44,46,48.②
3.测量某地垂直地面方向上海拔500m以下的大气温度,得到从距离地面20m起每升高100m处的大气温度(单位:℃)依次为
25,24,23,22,21. ③
4.某人向银行贷款a万元,贷款时间为n年.如果个人贷款月利率为r,那么按照等额本金方式还款,他从某月开始,每月应还本金b(=12n)元,每月支付给银行的利息(单位:元)依次为
ar,ar-br,ar-2br,ar-3br,... ④
数列②-④是否也有这样的取值规律
新知探究
2
差
公差
an+1-an=d(n∈N*)或an-an-1=d(n≥2,n∈N*)
等差数列的递推公式
新知探究
练习1 判断下列数列是否为等差数列,若是,求出首项和公差
(1) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10
(2) 3,3,3,3,3,3
(3) 3x,6x,9x,12x,15x
(4)95,82,69,56,43,30
(5) 1,1.1,1.11,1.111,1.1111
(6) 1,-2,3,-4,5,-6
a1=3,公差 d=0 常数列
a1=3x 公差 d= 3x
×
a1=95 公差 d=-13
×
×
新知探究
练习2 判断题
(1)数列a,2a,3a,4a,…是等差数列 ( )
(2)数列a-2,2a-3,3a-4,4a-5,…是等差数列( )
(3)若an-an+1=3 (n∈N*),则{an}是公差为3的等差数列( )
(4)若a2-a1=a3-a2, 则数列{an}是等差数列( )
若an-an-1=an+1-an (n≥2,n∈N*),则数列{an}是等差数列( )
若an-an-1=an+2-an+1 (n≥2,n∈N*),则数列{an}是等差数列( )
1,2,5,6,9,10,…
新知探究
练习3 在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2 ,( ) , 4
(2)-12,( ) ,0
(3)a,( ),b
3
-6
新知探究
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列,这时A叫做a与b的等差中项。
2. 等差中项
由等差数列的定义可知
… …
新知探究
求等差数列1,4,7,10,13,16,…的通项公式
新知探究
如果一个数列a1,a2,a3,...,an,...是等差数列,它的公差是d,求这个数列通项公式?
解:
n=1时亦适合
迭代法
新知探究
如果一个数列a1,a2,a3,...,an,...是等差数列,它的公差是d,求这个数列通项公式?
解:
a2-a1=d
a3-a2=d
a4-a3=d
…
an-an-1=d (n ≥ 2)
累加以上n-1个式子得
an-a1=(n-1)d
又∵当n=1时,上式也成立
∴an=a1+(n-1)d
累加法
首项a1公差d的等差数列{an}的通项公式为
练习4 求下列等差数列的通项公式
(1)9,18,27,36,45,54,63,72...
(2)38,40,42,44,46,48...
(3)25,24,23,22,21.
(1)an=9+(n-1)×9=9n
(2)an=38+(n-1)×2=2n+36
(3)an=25+(n-1)×(-1)=-n+26
等差数列的通项公式的一般形式:an=am+(n-m)d
3. 等差数列的通项公式
a1 、an、n、d知三求一
新知探究
课堂巩固
例1.(1)已知等差数列{an}的通项公式为an =5-2n,
求{an}公差和首项;
(2)求等差数列8,5,2....的第20项
分析:(2)可以先根据数列的两个已知项求出通项公式,再利用通项公式求数列的第20项
解:(2)由已知条件,得d=5-8=-3.
把a1=8,d=-3代入an=a1+(n-1)d,
得an=8-3(n-1)=11-3n.
把n=20代入上式,得a20=11-3×20=-49.
所以,这个数列的第20项是-49.
课堂巩固
例2.-401是不是等差数列 -5,-9,-13,…,的项?如果是,是第几项?
分析:先求出数列的通项公式,它是一个关于n的方程,再看-401是否能使这个方程有正整数解.
解:由a1=-5,d=-9-(-5)=-4,
所以数列的通项公式为an=-5-4(n-1)=-4n-1.
令-4n-1=-401,解得n=100.
所以,-401是这个数列的项,是第100项。
课堂巩固
在等差数列中,已知a5=10,a12=31,求首项与公差.
解:设数列的首项为a1与公差为d
由题意可知
即这个等差数列的首项是-2,公差是3.
归纳:在等差数列{an}的通项公式中a1、d、an、n,知三求二
课堂巩固
P15课本练习4 已知在等差数列中,a4+a8=20,a7=12,求a4.
解:设数列的首项为a1与公差为d
由题意可知
∴这个等差数列的通项公式为an=0+(n-1)×2=2n-2
则a4=2×4-2=6
解得
课堂小结
从第2项起,每一项与它的前一项的差等于同一个常数
等差数列的定义
由三个数a,A,b组成的等差数列,A叫做a与b的等差中项。
等差中项
首项a1公差d,的等差数列{an}的通项公式为
通项公式
迭代法、累加法
通项公式的推导方法
P15 课本 练习 3、5
课后作业
