陕西省咸阳市旬邑县高级中学2021-2022学年高二上学期12月月考数学试题(Word版含答案)
文档属性
| 名称 | 陕西省咸阳市旬邑县高级中学2021-2022学年高二上学期12月月考数学试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 00:00:00 | ||
图片预览




文档简介
旬邑县高级中学2021-2022学年高二上学期12月月考
数学试卷
一、单选题
1.圆 关于直线 对称的圆的方程为( )
A. B.
C. D.
2.执行如图所示的程序框图,输出的 值为( )
A. B. C. D.
3.设 ,那么 的值为( )
A. B. C. D. -1
4.已知数列{an}是递增的等比数列,a4=4a2 , a1+a5=17,则S2019-2a2019的值为( )
A. 1 B. -1 C. D.
5.已知命题 ,则命题 的否定为( )
A. B.
C. D.
6.如果 恒成立,则实数k的取值范围是( )
A. -1≤k≤0 B. -1≤k<0 C. -17.已知m和n是两条不同的直线, 和 是两个不重合的平面,下面给出的条件中一定能推出 的是( )
A. 且 B. 且
C. 且 D. 且
8.若函数 为增函数,则实数 的取值范围是( )
A. B. C. D.
9.定积分 的值是( )
A. B. C. 0 D.
10.德国数学家科拉茨 年提出了一个著名的猜想:任给一个正整数 ,如果 是偶数,就将它减半(即 );如果 是奇数,则将它乘 加 (即 ),不断重复这样的运算,经过有限步后,一定可以得到 .对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数 (首项)按照上述规则施行变换后的第 项为 (注: 可以多次出现),则 的所有不同值的个数为( )
A. B. C. D.
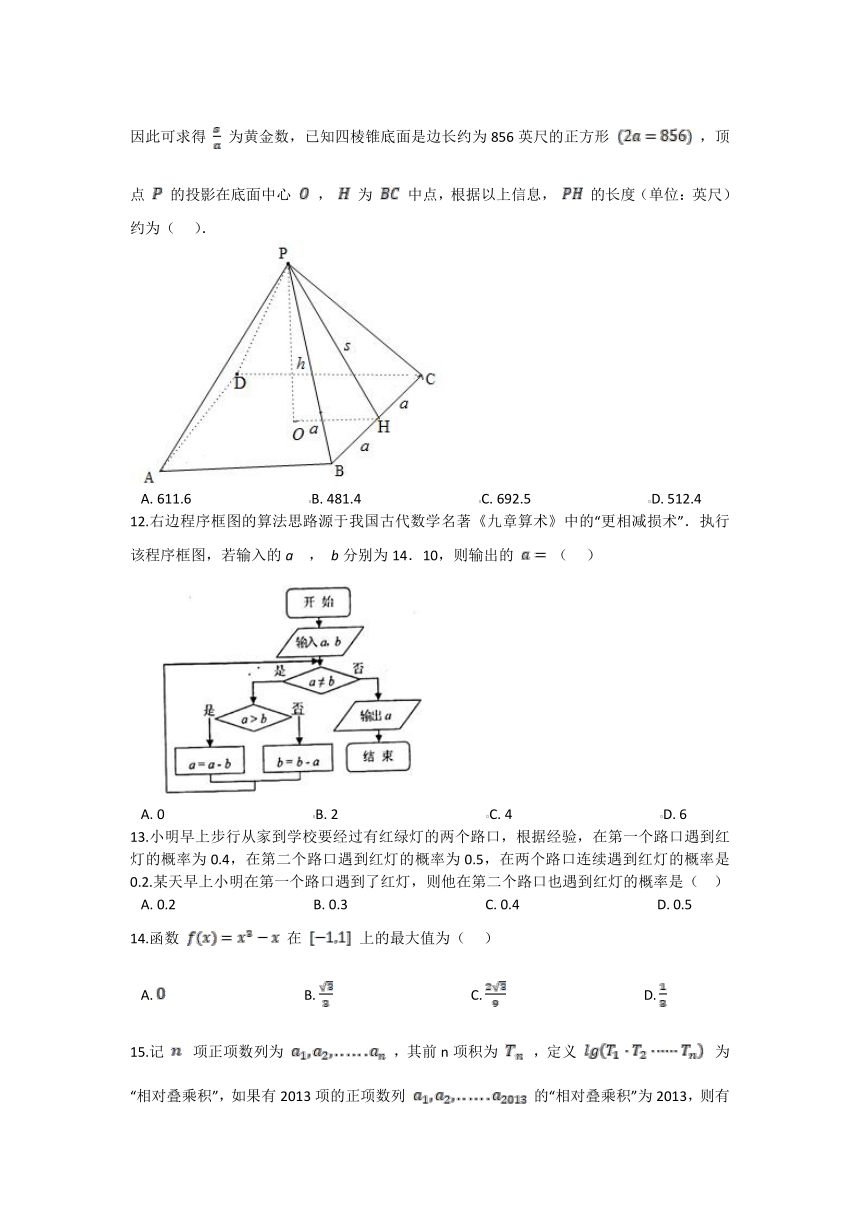
11.胡夫金字塔的形状为四棱锥,1859年,英国作家约翰·泰勒(JohnTaylor,1781-1846)在其《大金字塔》一书中提出:古埃及人在建造胡夫金字塔时利用黄金比例 ,泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的每一个侧面的面积都等于金字塔高的平方.如图,若 ,则由勾股定理, ,即 ,因此可求得 为黄金数,已知四棱锥底面是边长约为856英尺的正方形 ,顶点 的投影在底面中心 , 为 中点,根据以上信息, 的长度(单位:英尺)约为( ).
A. 611.6 B. 481.4 C. 692.5 D. 512.4
12.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a , b分别为14.10,则输出的 ( )
A. 0 B. 2 C. 4 D. 6
13.小明早上步行从家到学校要经过有红绿灯的两个路口,根据经验,在第一个路口遇到红灯的概率为0.4,在第二个路口遇到红灯的概率为0.5,在两个路口连续遇到红灯的概率是0.2.某天早上小明在第一个路口遇到了红灯,则他在第二个路口也遇到红灯的概率是( )
A. 0.2 B. 0.3 C. 0.4 D. 0.5
14.函数 在 上的最大值为( )
A. B. C. D.
15.记 项正项数列为 ,其前n项积为 ,定义 为“相对叠乘积”,如果有2013项的正项数列 的“相对叠乘积”为2013,则有2014项的数列 的“相对叠乘积”为( )
A. 2014 B. 2016 C. 3042 D. 4027
二、多选题
16.下列说法正确的是( )
A. 方程 表示两条直线
B. 椭圆 的焦距为4,则
C. 曲线 关于坐标原点对称
D. 双曲线 的渐近线方程为
17.已知数列 , 满足 , ,且 , 是数列 的前n项和,则下列结论正确的有( )
A. , B. ,
C. , D. ,
18.若将函数 的图象所有点的横坐标缩短为原来的 (纵坐标不变),再把图像向左平移 ,最后向上平移1个单位得到函数 的图象,则下列说法正确的是( )
A. 的对称中心 B. 在区间 上单调递减
C. 是函数 图象的对称轴 D. 在 上的最小值为
19.古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数 ( 且 )的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.已知 , ,圆 : 上有且仅有一个点 满足 ,则 的取值可以为( )
A. 1 B. 2 C. 3 D. 5
20.已知双曲线C: (a>0,b>0)与直线y=kx交于A,B两点,点P为C上一动点,记直线PA,PB的斜率分别为kPA , kPB , C的左、右焦点分别为F1 , F2 . 若kPA kPB= ,且C的焦点到渐近线的距离为1,则下列说法正确的是( )
A. a=2
B. C的离心率为
C. 若PF1⊥PF2 , 则 PF1F2的面积为2
D. 若 PF1F2的面积为 ,则 PF1F2为钝角三角形
三、填空题
21.关于x的不等式(2﹣a)x2﹣2(a﹣2)x+4>0对一切实数x都成立,则a的范围是 .
22.已知数列 满足 , , ,且 ,记 为数列 的前 项和,则 ________.
23.已知点 , ,若直线 与线段 相交,则 的取值范围是________.
24.已知倾斜角为α的直线l与直线x+2y﹣3=0垂直,则cos( ﹣2α)的值为 .
25.设函数 .若对任意实数 ,不等式 恒成立,则 .
四、解答题
26.已知在平面直角坐标系 中,点 ,直线 : .圆 的半径为1,圆心 在直线 上.
(1)若直线 与圆 相切,求圆 的标准方程;
(2)已知动点 ,满足 ,说明 的轨迹是什么?若点 同时在圆 上,求圆心 的横坐标 的取值范围.
27.设椭圆C: ( )的离心率为 ,焦距为2,过右焦点F的直线l与椭圆交于A,B两点,点M(2,0),设直线MA与直线MB的斜率分别为k1 , k2 .
(1)求椭圆方程;
(2)当直线l垂直x轴时,k1与k2有何关系?
(3)随着直线l的变化,k1+k2是否为定值?请说明理由.
28.如图所示,在四棱锥 中,底面 为矩形, 平面 ,点 在线段 上, 平面 .
(Ⅰ)证明: 平面 ;
(Ⅱ)若 ,求二面角 的正切值.
29.为了解成都市某区居民对接种新冠疫苗的态度,某机构日前通过社交媒体,进行了问卷调查,结果显示,多达73.4%的该区受访者最担心接种疫苗后会有副作用.其实任何一种疫苗都有一定的副作用,接种新型冠状病毒疫苗后也是有一定副作用的,这跟个人的体质有关系,有的人会出现副作用,而有的人不会出现副作用.在接种新冠疫苗的副作用中,有发热、疲乏、头痛等表现.为了了解接种某种疫苗后是否会出现疲乏症状的副作用,某组织随机抽取了该区1000人进行调查,得到统计数据如下:
无疲乏症状 有疲乏症状 总计
未接种疫苗 500 100 600
接种疫苗 x y n
总计 800 m 1000
(1)求 列联表中的数据 , , , 的值,并确定能否有99%的把握认为有疲乏症状与接种此种疫苗有关.
(2)从接种疫苗的 人中按是否有疲乏症状,采用分层抽样的方法抽出4人,再从4人中随机抽取2人做进一步调查.若初始总分为10分,抽到的2人中,每有一人有疲乏症状减1分,每有一人没有疲乏症状加2分,求得分结果总和为11的概率.
附: ,
P(K2≥k0) 0.150 0.100 0.050 0.025 0.010
k0 2.072 2.706 3.841 5.024 6.635
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 D
3.【答案】 A
4.【答案】 B
5.【答案】 C
6.【答案】 C
7.【答案】 B
8.【答案】 A
9.【答案】 C
10.【答案】 D
11.【答案】 C
12.【答案】 B
13.【答案】 D
14.【答案】 C
15.【答案】 D
二、多选题
16.【答案】 A,C,D
17.【答案】 B,D
18.【答案】 C,D
19.【答案】 A,D
20.【答案】 A,D
三、填空题
21.【答案】 (﹣2,2] 22.【答案】
23.【答案】 24.【答案】 ﹣ 25.【答案】
四、解答题
26.【答案】 (1)解:因为圆心C在直线l上,所以圆心C可设为(a,2a-4),
由题意可得 ,即 ,
所以 ,
解得 或 ,
所以圆心C的坐标为(3,2)或 ,
所以圆C的标准方程为 或
(2)解:由 ,得
化简得: ,
即 ,
所以动点M的轨迹是以D (0,-1)为圆心,半径是2的圆,
若点M同时在圆C上,则圆C与圆D有公共点,
则 ,
即
整理得:
解得 ,
所以圆心C的横坐标a的取值范围为[0, ].
27.【答案】 (1)解:由题意得 ,解得 ,
所以 ,
所以椭圆方程为 ,
(2)解:当直线l垂直x轴时,直线 的方程为 ,
当 时, , ,得 ,
所以 ,
因为 M(2,0),
所以 ,
所以 ,
(3)解:直线 为 , ,
由 ,得 ,
所以 ,
所以
,
所以 为定值
28.【答案】 解:(Ⅰ)证明 ∵PA⊥平面ABCD,BD 平面ABCD,
∴PA⊥BD.
同理由PC⊥平面BDE,可证得PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.
(Ⅱ解 :如图,
分别以射线AB,AD,AP为x轴、y轴、z轴的正半轴建立空间直角坐标系.
由(1)知BD⊥平面PAC,
又AC 平面PAC,∴BD⊥AC.
故矩形ABCD为正方形,
∴AB=BC=CD=AD=2.
∴A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,1).
∴ =(2,0,-1), =(0,2,0), =(-2,2,0).
设平面PBC的一个法向量为n=(x,y,z),则
∴取x=1得n=(1,0,2).
∵BD⊥平面PAC,
∴ =(-2,2,0)为平面PAC的一个法向量.
cos=
设二面角B-PC-A的平面角为α,由图知0<α< ,
∴cos α= ,sin α=
∴tan α= =3,即二面角B-PC-A的正切值为3.
29.【答案】 (1)由题意得: , ,
, ,
因为 .
所以有 的把握认为有疲乏症状与接种此种疫苗有关.
(2)从接种疫苗的 人中按是否有疲乏症状,采用分层抽样的方法抽出4人,可知4人中无疲乏症状的有6人,记为 ,有疲乏症状的有2人,记为 ,从4人中随机抽取2人,总基本事件有: 共6件,当这2人中恰有1人有疲乏症状时,得分为11分,记“得分结果总和为11”为事件M,事件M包括了3件基本事件,则 .
数学试卷
一、单选题
1.圆 关于直线 对称的圆的方程为( )
A. B.
C. D.
2.执行如图所示的程序框图,输出的 值为( )
A. B. C. D.
3.设 ,那么 的值为( )
A. B. C. D. -1
4.已知数列{an}是递增的等比数列,a4=4a2 , a1+a5=17,则S2019-2a2019的值为( )
A. 1 B. -1 C. D.
5.已知命题 ,则命题 的否定为( )
A. B.
C. D.
6.如果 恒成立,则实数k的取值范围是( )
A. -1≤k≤0 B. -1≤k<0 C. -1
A. 且 B. 且
C. 且 D. 且
8.若函数 为增函数,则实数 的取值范围是( )
A. B. C. D.
9.定积分 的值是( )
A. B. C. 0 D.
10.德国数学家科拉茨 年提出了一个著名的猜想:任给一个正整数 ,如果 是偶数,就将它减半(即 );如果 是奇数,则将它乘 加 (即 ),不断重复这样的运算,经过有限步后,一定可以得到 .对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数 (首项)按照上述规则施行变换后的第 项为 (注: 可以多次出现),则 的所有不同值的个数为( )
A. B. C. D.
11.胡夫金字塔的形状为四棱锥,1859年,英国作家约翰·泰勒(JohnTaylor,1781-1846)在其《大金字塔》一书中提出:古埃及人在建造胡夫金字塔时利用黄金比例 ,泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的每一个侧面的面积都等于金字塔高的平方.如图,若 ,则由勾股定理, ,即 ,因此可求得 为黄金数,已知四棱锥底面是边长约为856英尺的正方形 ,顶点 的投影在底面中心 , 为 中点,根据以上信息, 的长度(单位:英尺)约为( ).
A. 611.6 B. 481.4 C. 692.5 D. 512.4
12.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a , b分别为14.10,则输出的 ( )
A. 0 B. 2 C. 4 D. 6
13.小明早上步行从家到学校要经过有红绿灯的两个路口,根据经验,在第一个路口遇到红灯的概率为0.4,在第二个路口遇到红灯的概率为0.5,在两个路口连续遇到红灯的概率是0.2.某天早上小明在第一个路口遇到了红灯,则他在第二个路口也遇到红灯的概率是( )
A. 0.2 B. 0.3 C. 0.4 D. 0.5
14.函数 在 上的最大值为( )
A. B. C. D.
15.记 项正项数列为 ,其前n项积为 ,定义 为“相对叠乘积”,如果有2013项的正项数列 的“相对叠乘积”为2013,则有2014项的数列 的“相对叠乘积”为( )
A. 2014 B. 2016 C. 3042 D. 4027
二、多选题
16.下列说法正确的是( )
A. 方程 表示两条直线
B. 椭圆 的焦距为4,则
C. 曲线 关于坐标原点对称
D. 双曲线 的渐近线方程为
17.已知数列 , 满足 , ,且 , 是数列 的前n项和,则下列结论正确的有( )
A. , B. ,
C. , D. ,
18.若将函数 的图象所有点的横坐标缩短为原来的 (纵坐标不变),再把图像向左平移 ,最后向上平移1个单位得到函数 的图象,则下列说法正确的是( )
A. 的对称中心 B. 在区间 上单调递减
C. 是函数 图象的对称轴 D. 在 上的最小值为
19.古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数 ( 且 )的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.已知 , ,圆 : 上有且仅有一个点 满足 ,则 的取值可以为( )
A. 1 B. 2 C. 3 D. 5
20.已知双曲线C: (a>0,b>0)与直线y=kx交于A,B两点,点P为C上一动点,记直线PA,PB的斜率分别为kPA , kPB , C的左、右焦点分别为F1 , F2 . 若kPA kPB= ,且C的焦点到渐近线的距离为1,则下列说法正确的是( )
A. a=2
B. C的离心率为
C. 若PF1⊥PF2 , 则 PF1F2的面积为2
D. 若 PF1F2的面积为 ,则 PF1F2为钝角三角形
三、填空题
21.关于x的不等式(2﹣a)x2﹣2(a﹣2)x+4>0对一切实数x都成立,则a的范围是 .
22.已知数列 满足 , , ,且 ,记 为数列 的前 项和,则 ________.
23.已知点 , ,若直线 与线段 相交,则 的取值范围是________.
24.已知倾斜角为α的直线l与直线x+2y﹣3=0垂直,则cos( ﹣2α)的值为 .
25.设函数 .若对任意实数 ,不等式 恒成立,则 .
四、解答题
26.已知在平面直角坐标系 中,点 ,直线 : .圆 的半径为1,圆心 在直线 上.
(1)若直线 与圆 相切,求圆 的标准方程;
(2)已知动点 ,满足 ,说明 的轨迹是什么?若点 同时在圆 上,求圆心 的横坐标 的取值范围.
27.设椭圆C: ( )的离心率为 ,焦距为2,过右焦点F的直线l与椭圆交于A,B两点,点M(2,0),设直线MA与直线MB的斜率分别为k1 , k2 .
(1)求椭圆方程;
(2)当直线l垂直x轴时,k1与k2有何关系?
(3)随着直线l的变化,k1+k2是否为定值?请说明理由.
28.如图所示,在四棱锥 中,底面 为矩形, 平面 ,点 在线段 上, 平面 .
(Ⅰ)证明: 平面 ;
(Ⅱ)若 ,求二面角 的正切值.
29.为了解成都市某区居民对接种新冠疫苗的态度,某机构日前通过社交媒体,进行了问卷调查,结果显示,多达73.4%的该区受访者最担心接种疫苗后会有副作用.其实任何一种疫苗都有一定的副作用,接种新型冠状病毒疫苗后也是有一定副作用的,这跟个人的体质有关系,有的人会出现副作用,而有的人不会出现副作用.在接种新冠疫苗的副作用中,有发热、疲乏、头痛等表现.为了了解接种某种疫苗后是否会出现疲乏症状的副作用,某组织随机抽取了该区1000人进行调查,得到统计数据如下:
无疲乏症状 有疲乏症状 总计
未接种疫苗 500 100 600
接种疫苗 x y n
总计 800 m 1000
(1)求 列联表中的数据 , , , 的值,并确定能否有99%的把握认为有疲乏症状与接种此种疫苗有关.
(2)从接种疫苗的 人中按是否有疲乏症状,采用分层抽样的方法抽出4人,再从4人中随机抽取2人做进一步调查.若初始总分为10分,抽到的2人中,每有一人有疲乏症状减1分,每有一人没有疲乏症状加2分,求得分结果总和为11的概率.
附: ,
P(K2≥k0) 0.150 0.100 0.050 0.025 0.010
k0 2.072 2.706 3.841 5.024 6.635
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 D
3.【答案】 A
4.【答案】 B
5.【答案】 C
6.【答案】 C
7.【答案】 B
8.【答案】 A
9.【答案】 C
10.【答案】 D
11.【答案】 C
12.【答案】 B
13.【答案】 D
14.【答案】 C
15.【答案】 D
二、多选题
16.【答案】 A,C,D
17.【答案】 B,D
18.【答案】 C,D
19.【答案】 A,D
20.【答案】 A,D
三、填空题
21.【答案】 (﹣2,2] 22.【答案】
23.【答案】 24.【答案】 ﹣ 25.【答案】
四、解答题
26.【答案】 (1)解:因为圆心C在直线l上,所以圆心C可设为(a,2a-4),
由题意可得 ,即 ,
所以 ,
解得 或 ,
所以圆心C的坐标为(3,2)或 ,
所以圆C的标准方程为 或
(2)解:由 ,得
化简得: ,
即 ,
所以动点M的轨迹是以D (0,-1)为圆心,半径是2的圆,
若点M同时在圆C上,则圆C与圆D有公共点,
则 ,
即
整理得:
解得 ,
所以圆心C的横坐标a的取值范围为[0, ].
27.【答案】 (1)解:由题意得 ,解得 ,
所以 ,
所以椭圆方程为 ,
(2)解:当直线l垂直x轴时,直线 的方程为 ,
当 时, , ,得 ,
所以 ,
因为 M(2,0),
所以 ,
所以 ,
(3)解:直线 为 , ,
由 ,得 ,
所以 ,
所以
,
所以 为定值
28.【答案】 解:(Ⅰ)证明 ∵PA⊥平面ABCD,BD 平面ABCD,
∴PA⊥BD.
同理由PC⊥平面BDE,可证得PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.
(Ⅱ解 :如图,
分别以射线AB,AD,AP为x轴、y轴、z轴的正半轴建立空间直角坐标系.
由(1)知BD⊥平面PAC,
又AC 平面PAC,∴BD⊥AC.
故矩形ABCD为正方形,
∴AB=BC=CD=AD=2.
∴A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,1).
∴ =(2,0,-1), =(0,2,0), =(-2,2,0).
设平面PBC的一个法向量为n=(x,y,z),则
∴取x=1得n=(1,0,2).
∵BD⊥平面PAC,
∴ =(-2,2,0)为平面PAC的一个法向量.
cos
设二面角B-PC-A的平面角为α,由图知0<α< ,
∴cos α= ,sin α=
∴tan α= =3,即二面角B-PC-A的正切值为3.
29.【答案】 (1)由题意得: , ,
, ,
因为 .
所以有 的把握认为有疲乏症状与接种此种疫苗有关.
(2)从接种疫苗的 人中按是否有疲乏症状,采用分层抽样的方法抽出4人,可知4人中无疲乏症状的有6人,记为 ,有疲乏症状的有2人,记为 ,从4人中随机抽取2人,总基本事件有: 共6件,当这2人中恰有1人有疲乏症状时,得分为11分,记“得分结果总和为11”为事件M,事件M包括了3件基本事件,则 .
同课章节目录
