陕西省咸阳市旬邑县高级中学2021-2022学年高一上学期12月月考数学试题(Word版含答案)
文档属性
| 名称 | 陕西省咸阳市旬邑县高级中学2021-2022学年高一上学期12月月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 16:03:19 | ||
图片预览


文档简介
旬邑县高级中学2021-2022学年高一上学期12月月考
数学试卷
一、单选题
1.已知函数 在 上单调递增,则实数 的取值范围为( )
A. B. C. D.
2.已知函数 的最小正周期为 ,且对 , 恒成立,若 ,则 的最小值是( )
A. B. C. D.
3.函数 y=lncosx() 的图象是( )
A. B.
C. D.
4.已知函数 ,则函数 ( )
A. 是奇函数,且在 上单增 B. 是奇函数,且在 上单减
C. 是偶函数,且在 上单增 D. 是偶函数,且在 上单减
5.已知函数 的部分图象如图所示,则 的值可以
A. B. C. D.
6.下列各组不等式中解集相同的是( )
A. 与
B. 与
C. 与
D. 与
7.已知等比数列 的前k项和为12,前2k项和为48,则前4k项和为( )
A. 324 B. 480 C. 108 D. 156
8.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型: ,其中K为最大确诊病例数.当I( )=0.95K时,标志着已初步遏制疫情,则 约为( )(ln19≈3)
A. 60 B. 63 C. 66 D. 69
9.三个数 , , 的大小关系为
A. B. C. D.
10.已知集合A={1,m2+1},B={2,4},则“m= ”是“A∩B={4}”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
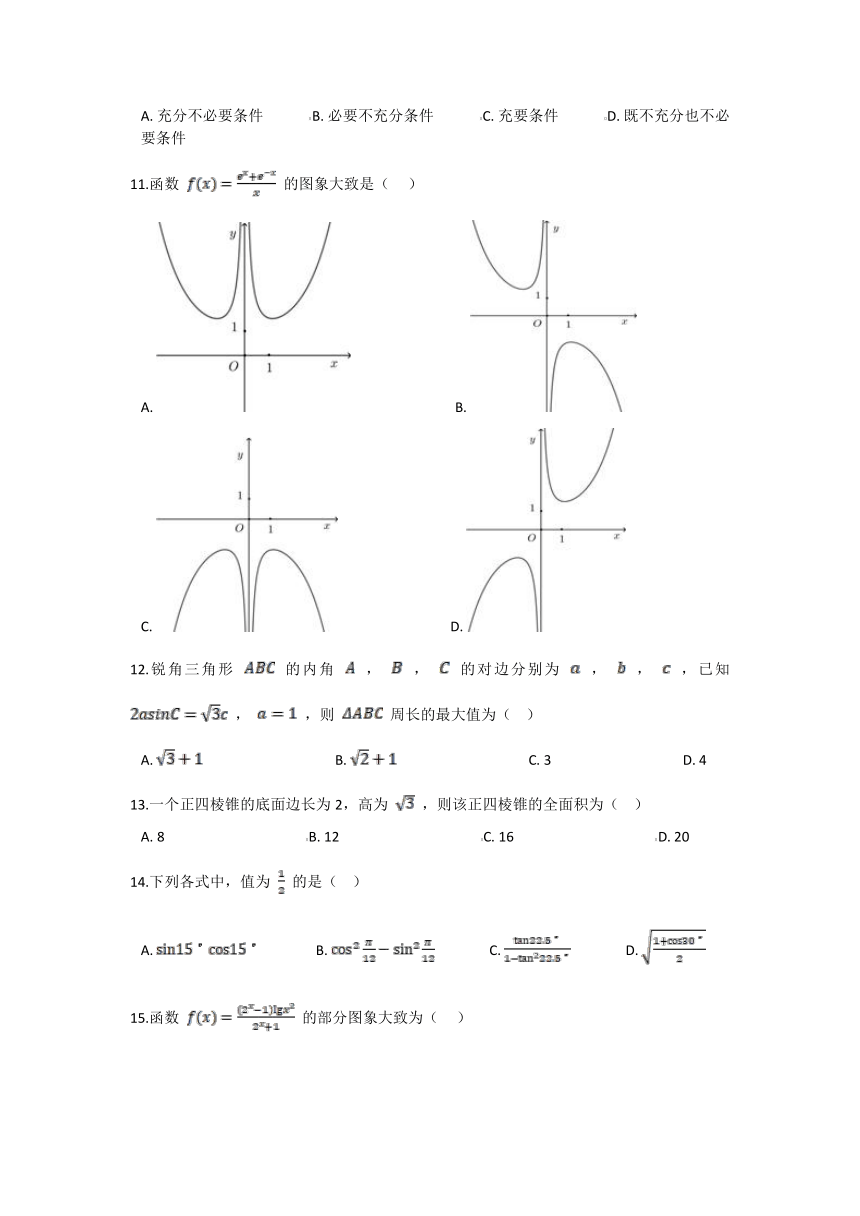
11.函数 的图象大致是( )
A. B.
C. D.
12.锐角三角形 的内角 , , 的对边分别为 , , ,已知 , ,则 周长的最大值为( )
A. B. C. 3 D. 4
13.一个正四棱锥的底面边长为2,高为 ,则该正四棱锥的全面积为( )
A. 8 B. 12 C. 16 D. 20
14.下列各式中,值为 的是( )
A. B. C. D.
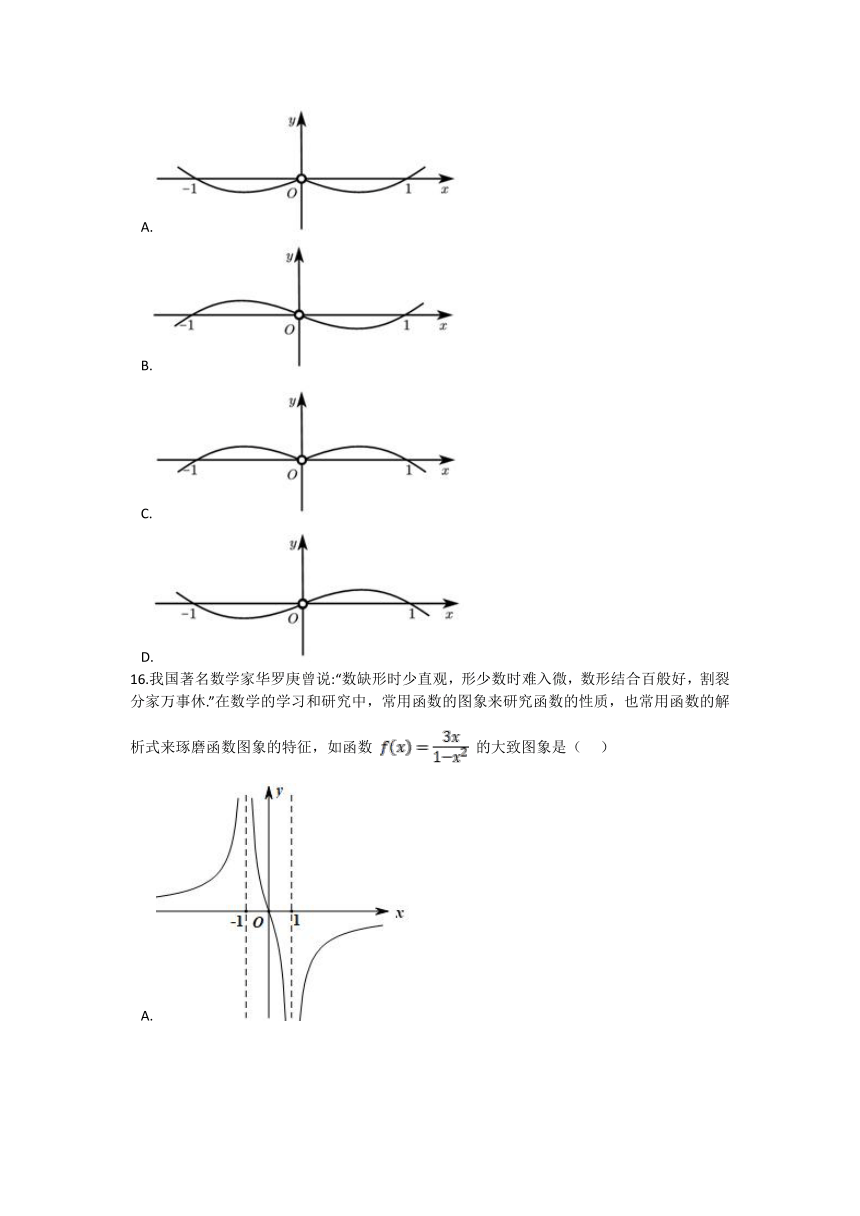
15.函数 的部分图象大致为( )
A.
B.
C.
D.
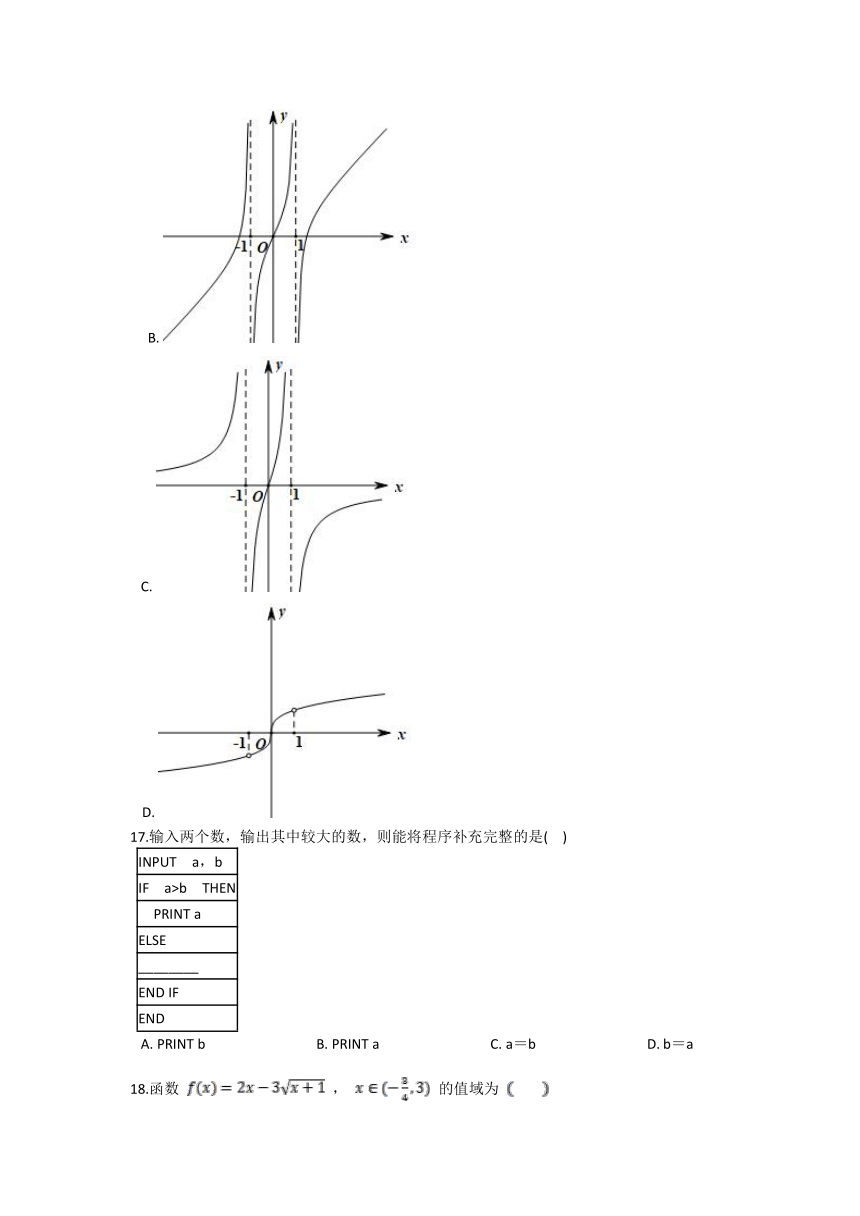
16.我国著名数学家华罗庚曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,割裂分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数图象的特征,如函数 的大致图象是( )
A.
B.
C.
D.
17.输入两个数,输出其中较大的数,则能将程序补充完整的是( )
INPUT a,b
IF a>b THEN
PRINT a
ELSE
________
END IF
END
A. PRINT b B. PRINT a C. a=b D. b=a
18.函数 , 的值域为
A. B. C. D.
19.已知 是定义在R上的偶函数,且 若当 时, ,则 ( )
A. B. 6 C. D.
20. 的边 所在直线上有一点 ,满足 ,则 可表示为( )
A. B. C. D.
二、填空题
21.已知等比数列{an},首项为3,公比为 ,前n项之积最大,则n= .
22.函数 ,若 ,则 ________
23.某购物商场计划在商场附近租赁一个仓库,已知仓库的月租赁费用m(万元)与商场到仓库的距离x(千米)成反比,且 时, ,每月从仓库往商场运送商品的费用n(万元)与x(千米)满足 ,若该商场每月这两项的支出总共11万元,则仓库到商场的距离为________千米.
24.设函数 是定义在 上的偶函数,记 ,且函数 在区间 上是增函数,则不等式 的解集为________
25.已知函数 的定义域为 ,则函数 的定义域为 .
三、解答题
26.设函数f(x)=x2+4tx+t-1.
(1)当t=1时,求函数f(x)在区间[-3,1]中的值域;
(2)若x∈[1,2]时,f(x)>0恒成立,求t的取值范围.
27.已知四棱锥 ,底面 是 ,边长为 的菱形,又 底面 ,且 , , 分别为棱 , 的中点.
(1)求证: 平面 ;
(2)求点 到平面 的距离.
28.在 中,已知
(1)试确定 的形状;
(2)求 的取值范围.
29.已知函数 是奇函数.
(1)求 的值并判断 的单调性;
(2)当 时,不等式 恒成立,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 C
2.【答案】 A
3.【答案】 A
4.【答案】 A
5.【答案】 A
6.【答案】 B
7.【答案】 B
8.【答案】 C
9.【答案】 A
10.【答案】 A
11.【答案】 D
12.【答案】 C
13.【答案】 B
14.【答案】 C
15.【答案】 B
16.【答案】 C
17.【答案】 A
18.【答案】 C
19.【答案】 B
20.【答案】 C
二、填空题
21.【答案】 3
22.【答案】
23.【答案】 2或3
24.【答案】
25.【答案】
三、解答题
26.【答案】 (1)解:当 时, ,
∴ 在区间 上单调递减,在 上单调递增,
∵ , ,
∴ ; ,
故值域为
(2)解: ,
当 ,即 时, ,∴ ;
当 ,即 时, ,无解;
当 ,即 时, ,∴ ,舍去;
综上, 的取值范围为
27.【答案】 (1)证明:如下图,取 中点为 ,分别连接 , ,
为 的中点,底面 是菱形,
∴ , ,
又 , 分别为 , 中点,
∴ , ,∴四边形 是平行四边形,
∴ , 平面 , 平面 ,
∴ 平面
(2)解:点 到平面 的距离等于点 到平面 的距离,设点 到平面 的距离为 ,
∵底面 是菱形, 为 的中点,
∴ ,又 ,∴ 平面 ,∴ ,
∴ ,∴ ,
即 ,解之得
28.【答案】 (1)解:由正弦定理得, ,所以 ①
因为 ,所以
所以 , ②
把②代入①得
所以 是直角三角形
(2)解:由(1)知 ,所以
所以 .
根据正弦定理得
因为 ,所以
即 的取值范围是
29.【答案】 (1)解:易知该函数的定义域为 ,又因为函数为奇函数,所以 , ,此时 在 上单调递减;
(2)解:由函数为奇函数,不等式 可化为 ,又函数在 上单调递减,所以 在 上恒成立,令 ,不等式 可化为 在 上恒成立,此时 不成立,当 时,不等式可转化为 ,又 在 上单调递减,所以当 时, 有最小值 ,所以 .
数学试卷
一、单选题
1.已知函数 在 上单调递增,则实数 的取值范围为( )
A. B. C. D.
2.已知函数 的最小正周期为 ,且对 , 恒成立,若 ,则 的最小值是( )
A. B. C. D.
3.函数 y=lncosx() 的图象是( )
A. B.
C. D.
4.已知函数 ,则函数 ( )
A. 是奇函数,且在 上单增 B. 是奇函数,且在 上单减
C. 是偶函数,且在 上单增 D. 是偶函数,且在 上单减
5.已知函数 的部分图象如图所示,则 的值可以
A. B. C. D.
6.下列各组不等式中解集相同的是( )
A. 与
B. 与
C. 与
D. 与
7.已知等比数列 的前k项和为12,前2k项和为48,则前4k项和为( )
A. 324 B. 480 C. 108 D. 156
8.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型: ,其中K为最大确诊病例数.当I( )=0.95K时,标志着已初步遏制疫情,则 约为( )(ln19≈3)
A. 60 B. 63 C. 66 D. 69
9.三个数 , , 的大小关系为
A. B. C. D.
10.已知集合A={1,m2+1},B={2,4},则“m= ”是“A∩B={4}”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
11.函数 的图象大致是( )
A. B.
C. D.
12.锐角三角形 的内角 , , 的对边分别为 , , ,已知 , ,则 周长的最大值为( )
A. B. C. 3 D. 4
13.一个正四棱锥的底面边长为2,高为 ,则该正四棱锥的全面积为( )
A. 8 B. 12 C. 16 D. 20
14.下列各式中,值为 的是( )
A. B. C. D.
15.函数 的部分图象大致为( )
A.
B.
C.
D.
16.我国著名数学家华罗庚曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,割裂分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数图象的特征,如函数 的大致图象是( )
A.
B.
C.
D.
17.输入两个数,输出其中较大的数,则能将程序补充完整的是( )
INPUT a,b
IF a>b THEN
PRINT a
ELSE
________
END IF
END
A. PRINT b B. PRINT a C. a=b D. b=a
18.函数 , 的值域为
A. B. C. D.
19.已知 是定义在R上的偶函数,且 若当 时, ,则 ( )
A. B. 6 C. D.
20. 的边 所在直线上有一点 ,满足 ,则 可表示为( )
A. B. C. D.
二、填空题
21.已知等比数列{an},首项为3,公比为 ,前n项之积最大,则n= .
22.函数 ,若 ,则 ________
23.某购物商场计划在商场附近租赁一个仓库,已知仓库的月租赁费用m(万元)与商场到仓库的距离x(千米)成反比,且 时, ,每月从仓库往商场运送商品的费用n(万元)与x(千米)满足 ,若该商场每月这两项的支出总共11万元,则仓库到商场的距离为________千米.
24.设函数 是定义在 上的偶函数,记 ,且函数 在区间 上是增函数,则不等式 的解集为________
25.已知函数 的定义域为 ,则函数 的定义域为 .
三、解答题
26.设函数f(x)=x2+4tx+t-1.
(1)当t=1时,求函数f(x)在区间[-3,1]中的值域;
(2)若x∈[1,2]时,f(x)>0恒成立,求t的取值范围.
27.已知四棱锥 ,底面 是 ,边长为 的菱形,又 底面 ,且 , , 分别为棱 , 的中点.
(1)求证: 平面 ;
(2)求点 到平面 的距离.
28.在 中,已知
(1)试确定 的形状;
(2)求 的取值范围.
29.已知函数 是奇函数.
(1)求 的值并判断 的单调性;
(2)当 时,不等式 恒成立,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 C
2.【答案】 A
3.【答案】 A
4.【答案】 A
5.【答案】 A
6.【答案】 B
7.【答案】 B
8.【答案】 C
9.【答案】 A
10.【答案】 A
11.【答案】 D
12.【答案】 C
13.【答案】 B
14.【答案】 C
15.【答案】 B
16.【答案】 C
17.【答案】 A
18.【答案】 C
19.【答案】 B
20.【答案】 C
二、填空题
21.【答案】 3
22.【答案】
23.【答案】 2或3
24.【答案】
25.【答案】
三、解答题
26.【答案】 (1)解:当 时, ,
∴ 在区间 上单调递减,在 上单调递增,
∵ , ,
∴ ; ,
故值域为
(2)解: ,
当 ,即 时, ,∴ ;
当 ,即 时, ,无解;
当 ,即 时, ,∴ ,舍去;
综上, 的取值范围为
27.【答案】 (1)证明:如下图,取 中点为 ,分别连接 , ,
为 的中点,底面 是菱形,
∴ , ,
又 , 分别为 , 中点,
∴ , ,∴四边形 是平行四边形,
∴ , 平面 , 平面 ,
∴ 平面
(2)解:点 到平面 的距离等于点 到平面 的距离,设点 到平面 的距离为 ,
∵底面 是菱形, 为 的中点,
∴ ,又 ,∴ 平面 ,∴ ,
∴ ,∴ ,
即 ,解之得
28.【答案】 (1)解:由正弦定理得, ,所以 ①
因为 ,所以
所以 , ②
把②代入①得
所以 是直角三角形
(2)解:由(1)知 ,所以
所以 .
根据正弦定理得
因为 ,所以
即 的取值范围是
29.【答案】 (1)解:易知该函数的定义域为 ,又因为函数为奇函数,所以 , ,此时 在 上单调递减;
(2)解:由函数为奇函数,不等式 可化为 ,又函数在 上单调递减,所以 在 上恒成立,令 ,不等式 可化为 在 上恒成立,此时 不成立,当 时,不等式可转化为 ,又 在 上单调递减,所以当 时, 有最小值 ,所以 .
同课章节目录
