广东省佛山市重点高中2022届高三上学期第三次阶段联考数学试题(Word版含答案)
文档属性
| 名称 | 广东省佛山市重点高中2022届高三上学期第三次阶段联考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 771.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 16:00:12 | ||
图片预览




文档简介
佛山市重点高中2022届高三上学期第三次阶段联考
数学试卷
考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.已知集合, ,则
A. B. C. D.
2.不等式的解集是
A. B. C. D.
3.已知幂函数的图象经过点,则
A.2 B. C. D.
4.设为奇函数,且当时,,则当时,
A. B. C. D.
5.若点在直线上,则的最小值为
A.2 B.3 C.4 D.5
6.已知,则
A. B. C. D.
7.已知函数图象的一条对称轴为,则的最小值为
A.2 B.4 C.6 D.8
8.在上的值域为
A. B. C. D.
二、多选题
9.下列求导过程正确的是
A. B. C. D.
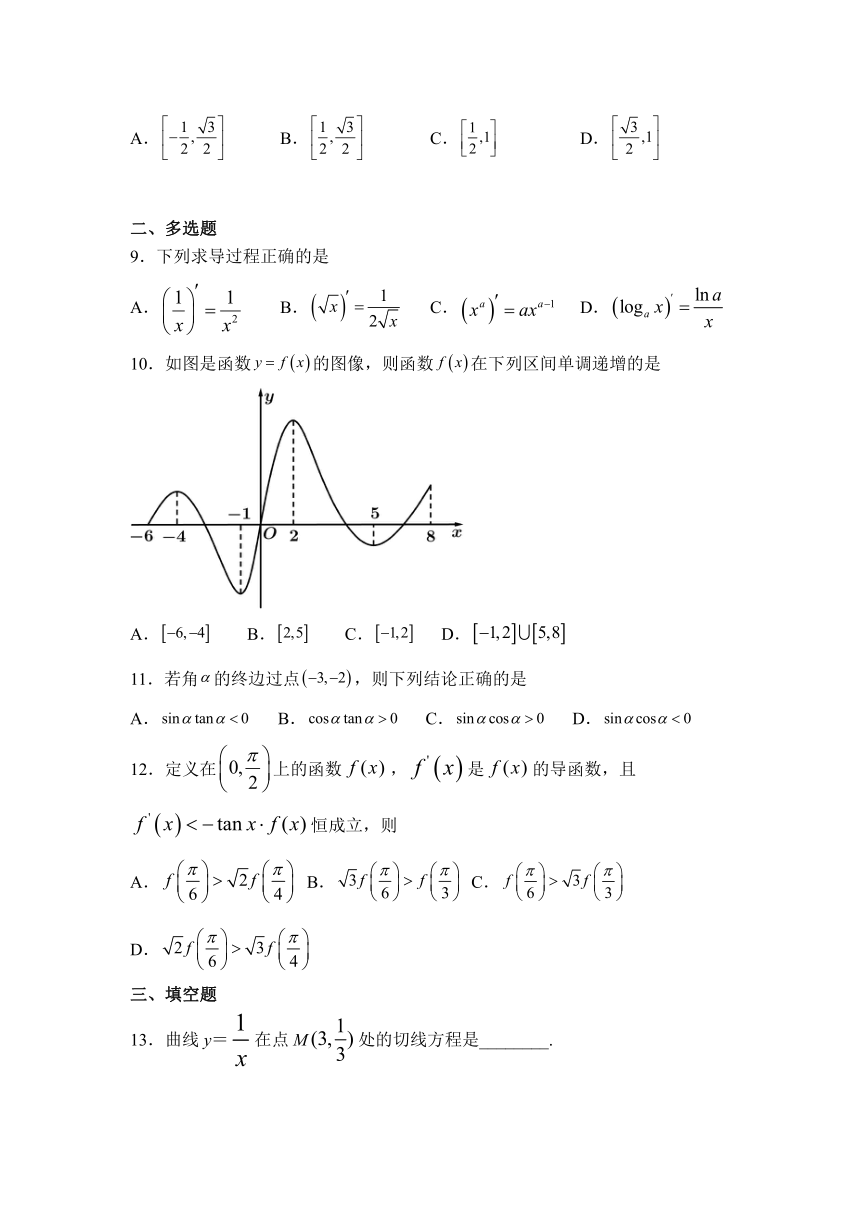
10.如图是函数的图像,则函数在下列区间单调递增的是
A. B. C. D.
11.若角的终边过点,则下列结论正确的是
A. B. C. D.
12.定义在上的函数,是的导函数,且恒成立,则
A. B. C. D.
三、填空题
13.曲线y=在点M处的切线方程是________.
14.已知角的终边上有一点,则______.
15.函数的零点有______个.
16.若函数为偶函数,则的一个值为________.(写出一个即可)
四、解答题
17.已知函数的部分图象如图所示.
(1)求的解析式;
(2)在中,角,,的对边分别为,,,若,求的取值范围.
18.已知数列是公差为2的等差数列,它的前n项和为Sn,且成等比数列.
(1)求的通项公式;
(2)求数列的前n项和.
19.某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织了数学学科考试,随机抽取50名学生的成绩并制成频率分布直方图如图所示.
(1)求的值,并估计高一年级所有学生数学成绩在频率分的学生所占的百分比;
(2)估计这50名学生数学成绩的平均数.(同一组中的数据以该组区间的中点值作代表)
20.如图,在四棱锥P﹣ABCD中,PA=PD,底面ABCD是矩形,侧面PAD⊥底面ABCD,E是AD的中点.
(1)求证:AD//平面PBC;
(2)求证:AB⊥平面PAD
21.已知圆.
(1)求圆关于直线对称的圆的方程;
(2)若直线过点与圆相交于,两点,求的面积的最大值,并求此时直线的方程.
22.已知.
(1)当时,求证:函数在上单调递增;
(2)若只有一个零点,求的取值范围.
参考答案
选择题题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B A A D C B B C BC AC AC CD
填空题题号 13 14 15 16
答案 x+9y-6=0 4 2 (答案不唯一)
17.(1);(2).
【详解】(1)由图知, ···········································1分
,·····················································2分
∴,. ···················································3分
,·············································4分
又,
∴, ·························································5分
∴. ···············································6分
(2)∵,当且仅当取“”, ···········8分
∵, ∴,············································9分
∴,··················································11分
∴.······································12分
18.(1),(2)
【详解】(1)因为数列是公差为2的等差数列,且成等比数列,
所以即,····························2分
解得,·······················································4分
所以;····················································6分
(2)由(1)得······························7分
·······································8分
所以·······················10分
···············································12分
19.(1),,(2)
【详解】(1)由频率分布直方图可知
,························2分
50名学生数学成绩在分的概率为,············4分
所以高一年级所有学生数学成绩在频率分的学生所占的百分比为。·····5分
(2)这50名学生数学成绩的平均数为
··········7分
···········································8分
20.(1)证明见解析;(2)证明见解析.
【详解】(1)证明:在四棱锥P﹣ABCD中,∵底面ABCD是矩形,
∴AD∥BC,·····················································2分
又AD平面PBC,BC平面PBC,·····································4分
∴AD∥平面PBC;·············································6分
(2)证明:∵底面ABCD是矩形,∴AB⊥AD,······················8分
又∵侧面PAD⊥底面ABCD,侧面PAD平面ABCD=AD,AB平面ABCD,······10分
∴AB⊥平面PAD. ··············································12分
21.(1)
(2)面积的最大值为,直线的方程为或.
(1)由圆可得圆心,半径,···················1分
圆心关于直线对称的点坐标为,······························2分
所以圆关于直线对称的圆的方程为.···························3分
(2)因为直线与圆相交,所以直线的斜率一定存在且不等于,
设直线的方程为:,即,··································4分
圆心到直线的距离,····································5分
,·············································6分
所以,···············7分
所以当时,最大为,·········································8分
,即,······································9分
解得:或,···········································10分
直线的方程为或,即或.······················11分
所以的面积的最大值为,直线的方程为或.···············12分
22.【分析】(1)当时,分别求、、,结合,可判断恒成立,即可求证;
(2)先证明为奇函数,,只需证明在上无零点,由(1)知,若可知符合题意,再讨论,利用单调性以及零点存在性定理即可求解.
(1)当时,,··························1分
,,··············································2分
所以在上单调递增,且,···································3分
所以当时,;当时,,·····························4分
所以在上单调递减,在上单调递增,且,·····5分
所以,所以在上单调递增;·······················6分
(2)因为, 所以为奇函数,,
要证明只有一个零点,只需证明在上无零点,
由(1)知:当时,,故,
令,则时,无零点,符合题意,···················8分
当时,,
故在上单调递减,则,无零点,符合题意,········9分
当时,,,,
所以在上单调递增,且,,
故存在唯一,使得,
所以在上单调递减,在上单调递增,····················11分
当时,,可得在上单调递减,所以,
取,时,令,
可得,即,且时,,
由零点存在性定理,在上至少存在一个零点,不符合题意,······················13分
综上所述:的取值范围为················································14分
数学试卷
考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.已知集合, ,则
A. B. C. D.
2.不等式的解集是
A. B. C. D.
3.已知幂函数的图象经过点,则
A.2 B. C. D.
4.设为奇函数,且当时,,则当时,
A. B. C. D.
5.若点在直线上,则的最小值为
A.2 B.3 C.4 D.5
6.已知,则
A. B. C. D.
7.已知函数图象的一条对称轴为,则的最小值为
A.2 B.4 C.6 D.8
8.在上的值域为
A. B. C. D.
二、多选题
9.下列求导过程正确的是
A. B. C. D.
10.如图是函数的图像,则函数在下列区间单调递增的是
A. B. C. D.
11.若角的终边过点,则下列结论正确的是
A. B. C. D.
12.定义在上的函数,是的导函数,且恒成立,则
A. B. C. D.
三、填空题
13.曲线y=在点M处的切线方程是________.
14.已知角的终边上有一点,则______.
15.函数的零点有______个.
16.若函数为偶函数,则的一个值为________.(写出一个即可)
四、解答题
17.已知函数的部分图象如图所示.
(1)求的解析式;
(2)在中,角,,的对边分别为,,,若,求的取值范围.
18.已知数列是公差为2的等差数列,它的前n项和为Sn,且成等比数列.
(1)求的通项公式;
(2)求数列的前n项和.
19.某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织了数学学科考试,随机抽取50名学生的成绩并制成频率分布直方图如图所示.
(1)求的值,并估计高一年级所有学生数学成绩在频率分的学生所占的百分比;
(2)估计这50名学生数学成绩的平均数.(同一组中的数据以该组区间的中点值作代表)
20.如图,在四棱锥P﹣ABCD中,PA=PD,底面ABCD是矩形,侧面PAD⊥底面ABCD,E是AD的中点.
(1)求证:AD//平面PBC;
(2)求证:AB⊥平面PAD
21.已知圆.
(1)求圆关于直线对称的圆的方程;
(2)若直线过点与圆相交于,两点,求的面积的最大值,并求此时直线的方程.
22.已知.
(1)当时,求证:函数在上单调递增;
(2)若只有一个零点,求的取值范围.
参考答案
选择题题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B A A D C B B C BC AC AC CD
填空题题号 13 14 15 16
答案 x+9y-6=0 4 2 (答案不唯一)
17.(1);(2).
【详解】(1)由图知, ···········································1分
,·····················································2分
∴,. ···················································3分
,·············································4分
又,
∴, ·························································5分
∴. ···············································6分
(2)∵,当且仅当取“”, ···········8分
∵, ∴,············································9分
∴,··················································11分
∴.······································12分
18.(1),(2)
【详解】(1)因为数列是公差为2的等差数列,且成等比数列,
所以即,····························2分
解得,·······················································4分
所以;····················································6分
(2)由(1)得······························7分
·······································8分
所以·······················10分
···············································12分
19.(1),,(2)
【详解】(1)由频率分布直方图可知
,························2分
50名学生数学成绩在分的概率为,············4分
所以高一年级所有学生数学成绩在频率分的学生所占的百分比为。·····5分
(2)这50名学生数学成绩的平均数为
··········7分
···········································8分
20.(1)证明见解析;(2)证明见解析.
【详解】(1)证明:在四棱锥P﹣ABCD中,∵底面ABCD是矩形,
∴AD∥BC,·····················································2分
又AD平面PBC,BC平面PBC,·····································4分
∴AD∥平面PBC;·············································6分
(2)证明:∵底面ABCD是矩形,∴AB⊥AD,······················8分
又∵侧面PAD⊥底面ABCD,侧面PAD平面ABCD=AD,AB平面ABCD,······10分
∴AB⊥平面PAD. ··············································12分
21.(1)
(2)面积的最大值为,直线的方程为或.
(1)由圆可得圆心,半径,···················1分
圆心关于直线对称的点坐标为,······························2分
所以圆关于直线对称的圆的方程为.···························3分
(2)因为直线与圆相交,所以直线的斜率一定存在且不等于,
设直线的方程为:,即,··································4分
圆心到直线的距离,····································5分
,·············································6分
所以,···············7分
所以当时,最大为,·········································8分
,即,······································9分
解得:或,···········································10分
直线的方程为或,即或.······················11分
所以的面积的最大值为,直线的方程为或.···············12分
22.【分析】(1)当时,分别求、、,结合,可判断恒成立,即可求证;
(2)先证明为奇函数,,只需证明在上无零点,由(1)知,若可知符合题意,再讨论,利用单调性以及零点存在性定理即可求解.
(1)当时,,··························1分
,,··············································2分
所以在上单调递增,且,···································3分
所以当时,;当时,,·····························4分
所以在上单调递减,在上单调递增,且,·····5分
所以,所以在上单调递增;·······················6分
(2)因为, 所以为奇函数,,
要证明只有一个零点,只需证明在上无零点,
由(1)知:当时,,故,
令,则时,无零点,符合题意,···················8分
当时,,
故在上单调递减,则,无零点,符合题意,········9分
当时,,,,
所以在上单调递增,且,,
故存在唯一,使得,
所以在上单调递减,在上单调递增,····················11分
当时,,可得在上单调递减,所以,
取,时,令,
可得,即,且时,,
由零点存在性定理,在上至少存在一个零点,不符合题意,······················13分
综上所述:的取值范围为················································14分
同课章节目录
