人教版七年级上册数学 第一章1.3.1 有理数的加法(共52张)
文档属性
| 名称 | 人教版七年级上册数学 第一章1.3.1 有理数的加法(共52张) |  | |
| 格式 | pptx | ||
| 文件大小 | 488.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 12:22:59 | ||
图片预览










文档简介
(共52张PPT)
有理数的加法(一)
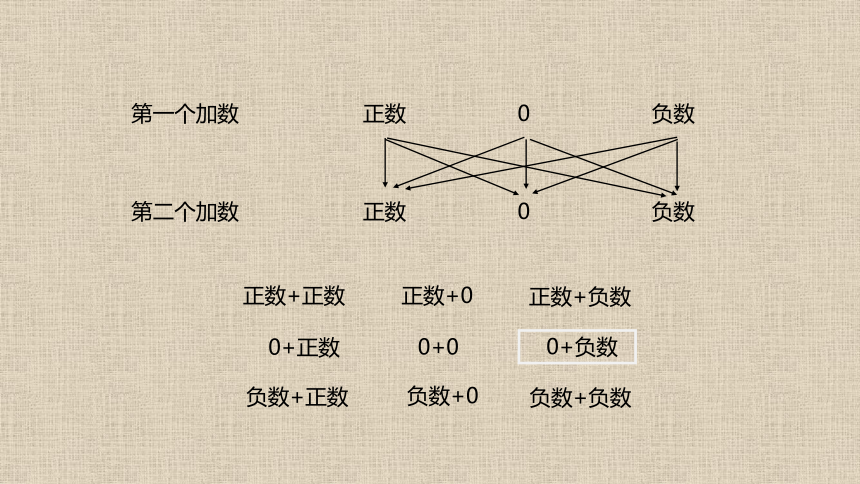
如果两个有理数做加法运算,那么会出现哪几种情况的算式?
第一个加数
正数
0
负数
第二个加数
正数
0
负数
第一个加数
正数
0
负数
第二个加数
正数
0
负数
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
第一个加数
正数
0
负数
第二个加数
正数
0
负数
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
三种类型:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数同 0 相加.
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
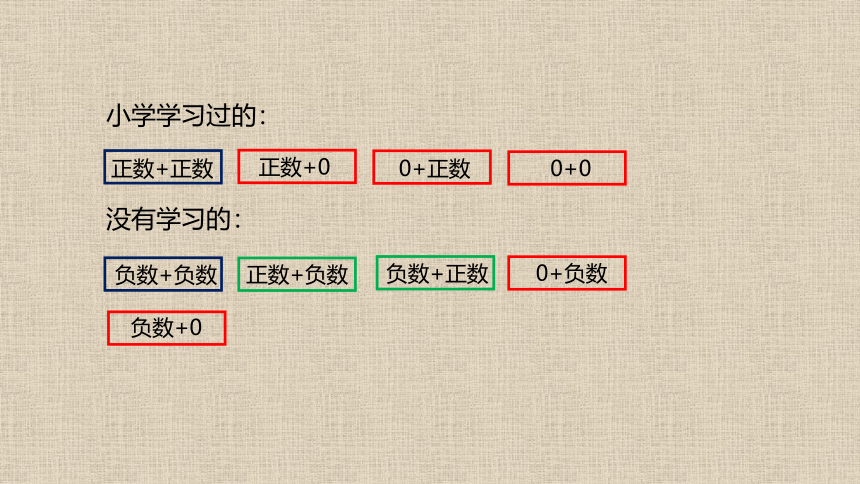
小学学习过的:
没有学习的:
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
一个数同 0 相加
小学学习过的:
没有学习的:
同号两个数相加
异号两个数相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
小学学习过的:
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
小学学习过的:
没有学习的:
(5)+ 0 = ?
0 +(5)= ?
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
小学学习过的:
没有学习的:
( 5)+ 0 = 5
0 +(5)= 5
类型一:一个数同 0 相加
(5)+ 0 =5
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型一:一个数同 0 相加
(5)+ 0 可以解释为:物体第 1 秒向左运动 5 m,第 2 秒原地不动,很显然,两秒后物体从起点向左运动了 5 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
(5)+ 0 = 5
类型一:一个数同 0 相加
(5)+ 0 可以解释为:物体第 1 秒向左运动 5 m,第 2 秒原地不动,很显然,两秒后物体从起点向左运动了 5 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
(5)+ 0 = 5
-5
-7 -6 -5 -4 -3 -2 -1 0 1
类型一:一个数同 0 相加
0 +(5)=5
类型一:一个数同 0 相加
0 +(5)= 5
-5
-7 -6 -5 -4 -3 -2 -1 0 1
类型一:一个数同 0 相加
(5)+ 0 =5
0 +(5)=5
结论:一个负数同 0 相加,仍得这个负数.
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
(5)+ 0 =5
0 +(5)=5
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
(5)+ 0 =5
0 +(5)=5
结论:一个数同 0 相加,仍得这个数.
类型一:一个数同 0 相加
小学学习过的:
5 + 3 = 8
类型二:同号两个数相加
小学学习过的:
5 + 3 = 8
没有学习的:
(5)+(3)= ?
类型二:同号两个数相加
小学学习过的:
5 + 3 = 8
没有学习的:
(5)+(3)=8
类型二:同号两个数相加
(5)+(3)= 8
类型二:同号两个数相加
(5)+(3)= 8
(5)+(3)可以解释为:物体先向左运动 5 m,再向左运动 3 m,很显然,两次运动后物体从起点向左运动了 8 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型二:同号两个数相加
(5)+(3)= 8
(5)+(3)可以解释为:物体先向左运动 5 m,再向左运动 3 m,很显然,两次运动后物体从起点向左运动了 8 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
-3
-5
-8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
类型二:同号两个数相加
(5)+(3)= 8
根据这个算式能否尝试总结负数与负数相加,
它的运算结果与两个加数有什么联系吗?
类型二:同号两个数相加
(5)+(3)= 8
根据这个算式能否尝试总结负数与负数相加,
它的运算结果与两个加数有什么联系吗?
符号
绝对值
类型二:同号两个数相加
根据这个算式能否尝试总结负数与负数相加,
它的运算结果与两个加数有什么联系吗?
符号
绝对值
结论:负数与负数相加,取负号,并把绝对值相加.
(5)+(3)= 8
类型二:同号两个数相加
5 + 3 = 8
(5)+(3)= 8
+
+
+
类型二:同号两个数相加
5 + 3 = 8
(5)+(3)= 8
+
+
+
结论:同号两数相加,取相同符号,并把绝对值相加.
类型二:同号两个数相加
(5)+ 3 = ?
5 + (3) = ?
5 + (5) = ?
类型三:异号两个数相加
(5)+ 3 =2
5 + (3) = 2
5 + (5) = 0
类型三:异号两个数相加
(5)+ 3 =2
类型三:异号两个数相加
(5)+ 3 可以解释为:物体先向左运动 5 m,再向右运动 3 m,
很显然,两次运动后物体从起点向左运动了 2 m.
(5)+ 3 =2
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型三:异号两个数相加
(5)+ 3 可以解释为:物体先向左运动 5 m,再向右运动 3 m,
很显然,两次运动后物体从起点向左运动了 2 m.
+3
-5
-2
-8 -7 -6 -5 -4 -3 -2 -1 0 1
(5)+ 3 =2
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型三:异号两个数相加
5 + (3) = 2
-3
+5
+2
-3 -2 -1 0 1 2 3 4 5 6
类型三:异号两个数相加
5 + (5) = 0
-5
+5
-3 -2 -1 0 1 2 3 4 5 6
类型三:异号两个数相加
5 +(5) = 0
(5)+ 3 =2
5 +(3) = 2
根据以上三个算式能否尝试总结异号两数相加的法则?
类型三:异号两个数相加
(5)+ 3 =2
5 +(3) = 2
5 +(5) = 0
+
+
+
结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得 0 .
类型三:异号两个数相加
1. 一个数同0相加,仍得这个数.
2. 同号两数相加,取相同的符号,并把绝对值相加.
3. 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值. 互为相反数的两个数相加得 0.
5 + 0 = 5
(5)+ 0 =5
5 + 3 = 8
(5)+(3)= 8
+
+
+
5 +(5) = 0
(5)+ 3 =2
5 +(3) = 2
+
+
+
有理数加法法则:
(1)(3)+ (9) =
做一做:
例1 计算:
(1)(3)+ (9) =
做一做:
例1 计算:
(1)(3)+ (9) =
做一做:
例1 计算:
( )
3+9
=12
(2)(4.7)+ 3.9 =
做一做:
例1 计算:
(2)(4.7)+ 3.9 =
做一做:
例1 计算:
(2)(4.7)+ 3.9 =
做一做:
例1 计算:
4.73.9
( )
= 0.8
(3) 6 + (6) =
做一做:
例1 计算:
(3) 6 + (6) =
做一做:
例1 计算:
0
(4)(6)+ 0 =
做一做:
例1 计算:
(4)(6)+ 0 =
做一做:
例1 计算:
6
有理数加法运算步骤:
(1)审;(两个加数是否是同号、异号,有无0.)
(2)定符号,定绝对值;
(3)算结果.
小结:
本节课内容:
1. 有理数的加法法则,以及进行有理数的加法运算时的步骤;
2. 在归纳、概括加法法则过程中体现了分类思想;在学习涉及负数的加法运算时,遵循由易到难,由简单到复杂的学习顺序。
有理数的加法(一)
如果两个有理数做加法运算,那么会出现哪几种情况的算式?
第一个加数
正数
0
负数
第二个加数
正数
0
负数
第一个加数
正数
0
负数
第二个加数
正数
0
负数
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
第一个加数
正数
0
负数
第二个加数
正数
0
负数
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
三种类型:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数同 0 相加.
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
小学学习过的:
没有学习的:
正数+正数
正数+0
正数+负数
0+0
0+正数
0+负数
负数+正数
负数+0
负数+负数
一个数同 0 相加
小学学习过的:
没有学习的:
同号两个数相加
异号两个数相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
小学学习过的:
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
小学学习过的:
没有学习的:
(5)+ 0 = ?
0 +(5)= ?
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
小学学习过的:
没有学习的:
( 5)+ 0 = 5
0 +(5)= 5
类型一:一个数同 0 相加
(5)+ 0 =5
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型一:一个数同 0 相加
(5)+ 0 可以解释为:物体第 1 秒向左运动 5 m,第 2 秒原地不动,很显然,两秒后物体从起点向左运动了 5 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
(5)+ 0 = 5
类型一:一个数同 0 相加
(5)+ 0 可以解释为:物体第 1 秒向左运动 5 m,第 2 秒原地不动,很显然,两秒后物体从起点向左运动了 5 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
(5)+ 0 = 5
-5
-7 -6 -5 -4 -3 -2 -1 0 1
类型一:一个数同 0 相加
0 +(5)=5
类型一:一个数同 0 相加
0 +(5)= 5
-5
-7 -6 -5 -4 -3 -2 -1 0 1
类型一:一个数同 0 相加
(5)+ 0 =5
0 +(5)=5
结论:一个负数同 0 相加,仍得这个负数.
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
(5)+ 0 =5
0 +(5)=5
类型一:一个数同 0 相加
5 + 0 = 5
0 + 5 = 5
0 + 0 = 0
(5)+ 0 =5
0 +(5)=5
结论:一个数同 0 相加,仍得这个数.
类型一:一个数同 0 相加
小学学习过的:
5 + 3 = 8
类型二:同号两个数相加
小学学习过的:
5 + 3 = 8
没有学习的:
(5)+(3)= ?
类型二:同号两个数相加
小学学习过的:
5 + 3 = 8
没有学习的:
(5)+(3)=8
类型二:同号两个数相加
(5)+(3)= 8
类型二:同号两个数相加
(5)+(3)= 8
(5)+(3)可以解释为:物体先向左运动 5 m,再向左运动 3 m,很显然,两次运动后物体从起点向左运动了 8 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型二:同号两个数相加
(5)+(3)= 8
(5)+(3)可以解释为:物体先向左运动 5 m,再向左运动 3 m,很显然,两次运动后物体从起点向左运动了 8 m.
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
-3
-5
-8
-8 -7 -6 -5 -4 -3 -2 -1 0 1
类型二:同号两个数相加
(5)+(3)= 8
根据这个算式能否尝试总结负数与负数相加,
它的运算结果与两个加数有什么联系吗?
类型二:同号两个数相加
(5)+(3)= 8
根据这个算式能否尝试总结负数与负数相加,
它的运算结果与两个加数有什么联系吗?
符号
绝对值
类型二:同号两个数相加
根据这个算式能否尝试总结负数与负数相加,
它的运算结果与两个加数有什么联系吗?
符号
绝对值
结论:负数与负数相加,取负号,并把绝对值相加.
(5)+(3)= 8
类型二:同号两个数相加
5 + 3 = 8
(5)+(3)= 8
+
+
+
类型二:同号两个数相加
5 + 3 = 8
(5)+(3)= 8
+
+
+
结论:同号两数相加,取相同符号,并把绝对值相加.
类型二:同号两个数相加
(5)+ 3 = ?
5 + (3) = ?
5 + (5) = ?
类型三:异号两个数相加
(5)+ 3 =2
5 + (3) = 2
5 + (5) = 0
类型三:异号两个数相加
(5)+ 3 =2
类型三:异号两个数相加
(5)+ 3 可以解释为:物体先向左运动 5 m,再向右运动 3 m,
很显然,两次运动后物体从起点向左运动了 2 m.
(5)+ 3 =2
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型三:异号两个数相加
(5)+ 3 可以解释为:物体先向左运动 5 m,再向右运动 3 m,
很显然,两次运动后物体从起点向左运动了 2 m.
+3
-5
-2
-8 -7 -6 -5 -4 -3 -2 -1 0 1
(5)+ 3 =2
一个物体向左右方向运动,我们规定向右为正,向左为负.比如:向右运动 5 m记作 5 m,向左运动 5 m记作5 m.
类型三:异号两个数相加
5 + (3) = 2
-3
+5
+2
-3 -2 -1 0 1 2 3 4 5 6
类型三:异号两个数相加
5 + (5) = 0
-5
+5
-3 -2 -1 0 1 2 3 4 5 6
类型三:异号两个数相加
5 +(5) = 0
(5)+ 3 =2
5 +(3) = 2
根据以上三个算式能否尝试总结异号两数相加的法则?
类型三:异号两个数相加
(5)+ 3 =2
5 +(3) = 2
5 +(5) = 0
+
+
+
结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得 0 .
类型三:异号两个数相加
1. 一个数同0相加,仍得这个数.
2. 同号两数相加,取相同的符号,并把绝对值相加.
3. 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值. 互为相反数的两个数相加得 0.
5 + 0 = 5
(5)+ 0 =5
5 + 3 = 8
(5)+(3)= 8
+
+
+
5 +(5) = 0
(5)+ 3 =2
5 +(3) = 2
+
+
+
有理数加法法则:
(1)(3)+ (9) =
做一做:
例1 计算:
(1)(3)+ (9) =
做一做:
例1 计算:
(1)(3)+ (9) =
做一做:
例1 计算:
( )
3+9
=12
(2)(4.7)+ 3.9 =
做一做:
例1 计算:
(2)(4.7)+ 3.9 =
做一做:
例1 计算:
(2)(4.7)+ 3.9 =
做一做:
例1 计算:
4.73.9
( )
= 0.8
(3) 6 + (6) =
做一做:
例1 计算:
(3) 6 + (6) =
做一做:
例1 计算:
0
(4)(6)+ 0 =
做一做:
例1 计算:
(4)(6)+ 0 =
做一做:
例1 计算:
6
有理数加法运算步骤:
(1)审;(两个加数是否是同号、异号,有无0.)
(2)定符号,定绝对值;
(3)算结果.
小结:
本节课内容:
1. 有理数的加法法则,以及进行有理数的加法运算时的步骤;
2. 在归纳、概括加法法则过程中体现了分类思想;在学习涉及负数的加法运算时,遵循由易到难,由简单到复杂的学习顺序。
