2021-2022学年人教版九年级数学上册24.1.4圆周角同步练习题(含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.1.4圆周角同步练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 370.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 12:43:26 | ||
图片预览
文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.1.4 圆周角 同步练习题
一、选择题
1.下列命题正确的是( )
A.同位角相等 B.相等的圆心角所对的弧相等
C.对角线相等的四边形是矩形 D.直角三角形斜边上的中线等于斜边的一半
2.如图,是的直径,弦于点E,连接,.若,则( )
A. B. C. D.
3.AB是⊙O的直径,C、D是圆上两点,∠BDC=32°,则∠AOC的度数为( )
A.32° B.64° C.116° D.128°
4.如图,半径为5的经过点C和点O,点B是y轴右侧的优弧上一点,,则点C的坐标为( )
A. B. C. D.
5.如图,,.若,,则的长为( )
A. B. C. D.4
6.如图,AB为的直径,AC为的弦,D是弧BC的中点,E是AC的中点.若,,则DE=( )
A. B.5 C. D.
7.如图,,是上直径两侧的两点.设,则( )
A. B. C. D.
8.如图,为的直径,以为斜边作等腰,连接交于点.若.则的长为( )
A. B. C. D.
9.如图,是⊙的直径,是⊙上两点,若,则的度数是( )
A. B. C. D.
10.如图,A,B,C是半径为1的⊙O上的三个点,若AB=,∠CAB=30°,则∠ABC的度数为( )
A.95° B.100° C.105° D.110°
二、填空题
11.在锐角三角形ABC中,∠A=30°,BC=2,设BC边上的高为h,则h的取值范围是 __________________.
12.如图,内接于⊙O,的角平分线交⊙O于D.若,则的长为____.
13.如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于______________.
14.如图,在平面直角坐标系中,点A在轴负半轴上,点B在轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________
15.如图,在⊙O中,AC=AB, 直径BC=2, , 则AD=___.
三、解答题
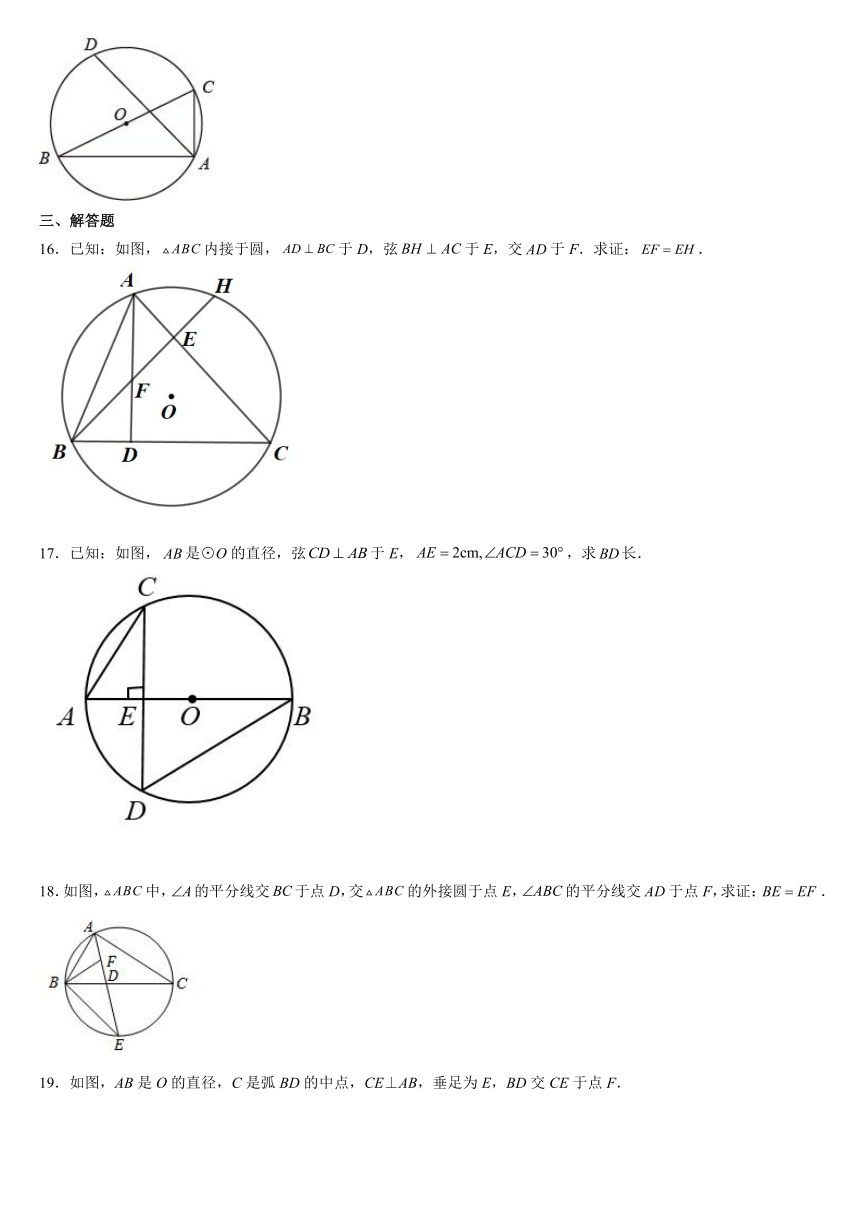
16.已知:如图,内接于圆,于D,弦于E,交于F.求证:.
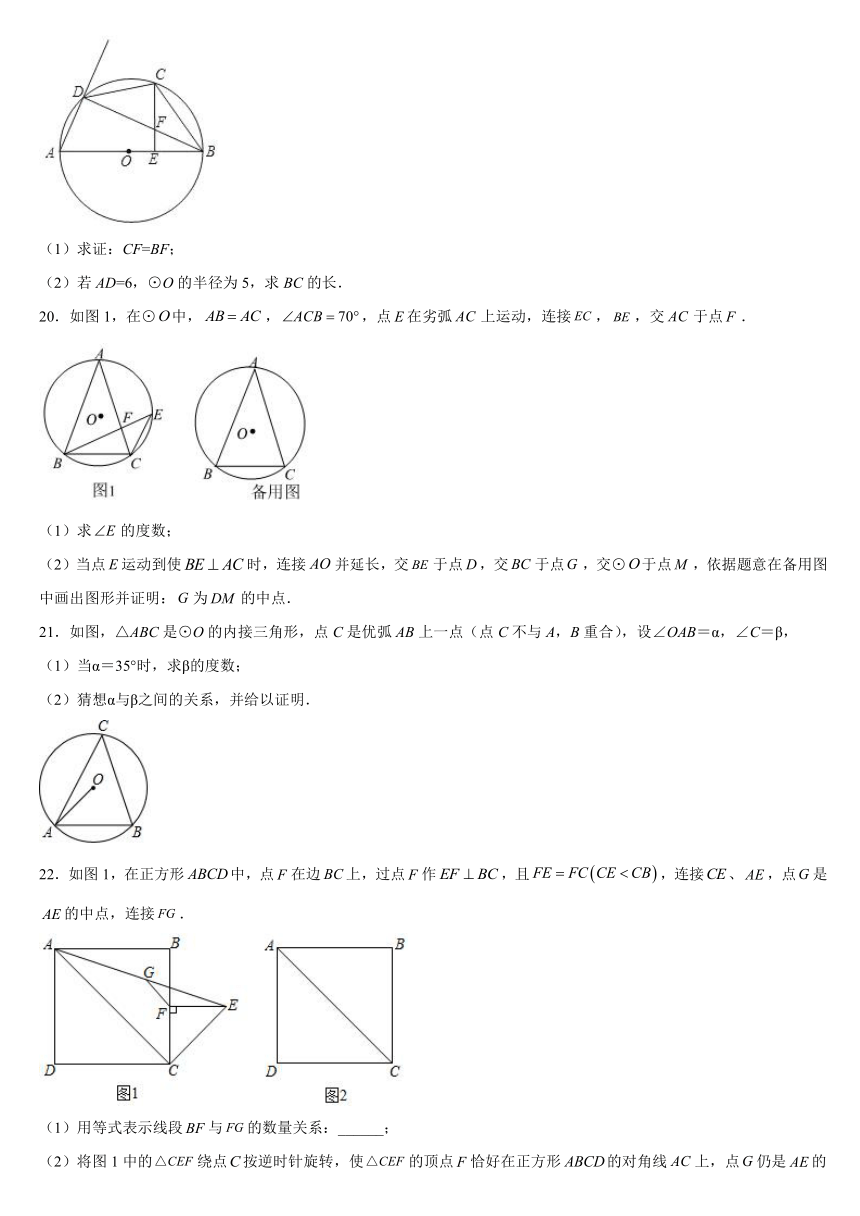
17.已知:如图,是⊙O的直径,弦于E,,求长.
18.如图,中,的平分线交于点D,交的外接圆于点E,的平分线交于点F,求证:.
19.如图,AB是O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,⊙O的半径为5,求BC的长.
20.如图1,在⊙中,,,点在劣弧上运动,连接,,交于点.
(1)求的度数;
(2)当点运动到使时,连接并延长,交于点,交于点,交⊙于点,依据题意在备用图中画出图形并证明:为的中点.
21.如图,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β,
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给以证明.
22.如图1,在正方形中,点在边上,过点作,且,连接、,点是的中点,连接.
(1)用等式表示线段与的数量关系:______;
(2)将图1中的绕点按逆时针旋转,使的顶点恰好在正方形的对角线上,点仍是的中点,连接、.
①在图2中,依据题意补全图形;
②用等式表示线段与的数量关系并证明.
23.如图,以BCG一边BC为直径作半圆交边BG,CG于A,D两点,连接AC,BD, O为圆心,连接AD并延长交BC的延长线于点F,已知∠G=67.5°,.
(1)求∠ABC的度数;
(2)证明CF=CA并直接写出的值;
(3)若四边形ABCD的面积为,求⊙O的半径.
【参考答案】
1.D
2.D
3.C
4.A
5.C
6.A
7.D
8.D
9.C
10.C
11.
12.
13.2
14.D(,1)
15.
16.连接,如图,
,
,
,,
,
,
,
,
,
,
17.解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE,∠AEC=∠DEB=90°,
∵∠B=∠ACD=30°,
在Rt△ACE中,AC=2AE=4cm,
∴(cm),
∴cm,
在Rt△BDE中,∠B=30°,
∴cm.
∴的长为cm.
18.BF平分∠ABC,
∠ABF=∠CBF,
AE平分∠BAC,
∠BAE=∠CAE,
又∠CAE=∠CBE,
∠BAE=∠CBE,
∠EBF=∠CBE+∠CBF,∠EFB=∠BAE+∠ABF,
∠EBF=∠EFB,
BE=EF.
19.(1)证明:连接AC,如图1所示:
∵C是弧BD的中点,
∴∠DBC=∠BAC,
在ABC中,∠ACB=90°,CE⊥AB,
∴∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,
∴∠BCE=∠DBC,
∴CF=BF;
(2)解:连接OC交BD于G,如图2所示:
∵AB是O的直径,AB=2OC=10,
∴∠ADB=90°,
∴BD==8,
∵C是弧BD的中点,
∴OC⊥BD,DG=BG=BD=4,
∵OA=OB,
∴OG是△ABD的中位线,
∴OG=AD=3,
∴CG=OC-OG=5-3=2,
在Rt△BCG中,
由勾股定理得:BC=.
20.解:(1)如图1,
∵,
∴,
∴,
∵,
∴.
(2)依据题意画图.
连接BM,CM.
∵AB=AC,
∴,
∴,
∴BM=CM,∠BAM=∠CAM=20°,
∴∠MBC=∠CAM=20°,
∵BE⊥AC,AM⊥BC,
∴∠BGD=∠AFD=90°,
∴∠BDG=∠ADF=70°,
∵∠BMA=∠ACB=70°,
∴∠BMA=∠BDG=70°,
∴BD=BM,
又∵BG⊥DM,
∴GD=GM.即:G为DM的中点.
21.解:(1)连接OB,
∵∠OAB=α=35°,
∴∠OBA=35°,
∴∠AOB=110°,
∴β=∠AOB=55°;
(2)结论:α+β=90°.
证明:∵∠AOB=180°-2α,β=∠AOB
∴β=90°-α,
∴α+β=90°.
22.解:(1)BF=,
理由是:如图1,连接BG,CG,
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=(360°﹣∠BFE)=(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=FG.
故答案为:BF=FG;
(2)①如图2所示,
②;理由如下:
如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=FG,
∴DF=FG.
23.(1)解:∵BC为直径,
∴∠CDB=90°,
∴∠GDB=90°,
∴ ,
∵ ,
∴,
∵,
∴∠DBG=∠DBC=22.5°,
∴;
(2)证明:∵BC为直径,
∴∠CAB=90°,
∵,
∴∠ACB=45°,
∴∠F+∠CAF=∠ACB=45°,
∵∠CAF=∠DBC=22.5°,
∴∠CAF=22.5°,
∴∠F=∠CAF=22.5°,
∴CF=CA,
在 中,
∵,∠ACB=45°,
∴,
∴AC=BC,
由勾股定理得:AC2+AB2=2AC2=BC2,
∴ ,
∴,
∴;
(3)解:∵∠G=67.5°,,
∴∠BCG=67.5,
∴∠BCG=∠G,
∴BC=BG,
∴△BCG是等腰三角形,
∵∠BDC=90°,即BD⊥CG,
∴CD=DG,
∴ ,
在 中,∠CAB=90°,
∵,
∴∠ACB=∠ABC=45°,
∴AC=AB,
由勾股定理得:AC2+AB2=2AB2=BC2,
∴ ,
设⊙O的半径为r,则BG=BC=2r,,
∴ ,
∴四边形ABCD的面积等于
,
∵四边形ABCD的面积为,
∴ ,
解得: 或 (舍去)
即设⊙O的半径为
一、选择题
1.下列命题正确的是( )
A.同位角相等 B.相等的圆心角所对的弧相等
C.对角线相等的四边形是矩形 D.直角三角形斜边上的中线等于斜边的一半
2.如图,是的直径,弦于点E,连接,.若,则( )
A. B. C. D.
3.AB是⊙O的直径,C、D是圆上两点,∠BDC=32°,则∠AOC的度数为( )
A.32° B.64° C.116° D.128°
4.如图,半径为5的经过点C和点O,点B是y轴右侧的优弧上一点,,则点C的坐标为( )
A. B. C. D.
5.如图,,.若,,则的长为( )
A. B. C. D.4
6.如图,AB为的直径,AC为的弦,D是弧BC的中点,E是AC的中点.若,,则DE=( )
A. B.5 C. D.
7.如图,,是上直径两侧的两点.设,则( )
A. B. C. D.
8.如图,为的直径,以为斜边作等腰,连接交于点.若.则的长为( )
A. B. C. D.
9.如图,是⊙的直径,是⊙上两点,若,则的度数是( )
A. B. C. D.
10.如图,A,B,C是半径为1的⊙O上的三个点,若AB=,∠CAB=30°,则∠ABC的度数为( )
A.95° B.100° C.105° D.110°
二、填空题
11.在锐角三角形ABC中,∠A=30°,BC=2,设BC边上的高为h,则h的取值范围是 __________________.
12.如图,内接于⊙O,的角平分线交⊙O于D.若,则的长为____.
13.如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于______________.
14.如图,在平面直角坐标系中,点A在轴负半轴上,点B在轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是________
15.如图,在⊙O中,AC=AB, 直径BC=2, , 则AD=___.
三、解答题
16.已知:如图,内接于圆,于D,弦于E,交于F.求证:.
17.已知:如图,是⊙O的直径,弦于E,,求长.
18.如图,中,的平分线交于点D,交的外接圆于点E,的平分线交于点F,求证:.
19.如图,AB是O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,⊙O的半径为5,求BC的长.
20.如图1,在⊙中,,,点在劣弧上运动,连接,,交于点.
(1)求的度数;
(2)当点运动到使时,连接并延长,交于点,交于点,交⊙于点,依据题意在备用图中画出图形并证明:为的中点.
21.如图,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β,
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给以证明.
22.如图1,在正方形中,点在边上,过点作,且,连接、,点是的中点,连接.
(1)用等式表示线段与的数量关系:______;
(2)将图1中的绕点按逆时针旋转,使的顶点恰好在正方形的对角线上,点仍是的中点,连接、.
①在图2中,依据题意补全图形;
②用等式表示线段与的数量关系并证明.
23.如图,以BCG一边BC为直径作半圆交边BG,CG于A,D两点,连接AC,BD, O为圆心,连接AD并延长交BC的延长线于点F,已知∠G=67.5°,.
(1)求∠ABC的度数;
(2)证明CF=CA并直接写出的值;
(3)若四边形ABCD的面积为,求⊙O的半径.
【参考答案】
1.D
2.D
3.C
4.A
5.C
6.A
7.D
8.D
9.C
10.C
11.
12.
13.2
14.D(,1)
15.
16.连接,如图,
,
,
,,
,
,
,
,
,
,
17.解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE,∠AEC=∠DEB=90°,
∵∠B=∠ACD=30°,
在Rt△ACE中,AC=2AE=4cm,
∴(cm),
∴cm,
在Rt△BDE中,∠B=30°,
∴cm.
∴的长为cm.
18.BF平分∠ABC,
∠ABF=∠CBF,
AE平分∠BAC,
∠BAE=∠CAE,
又∠CAE=∠CBE,
∠BAE=∠CBE,
∠EBF=∠CBE+∠CBF,∠EFB=∠BAE+∠ABF,
∠EBF=∠EFB,
BE=EF.
19.(1)证明:连接AC,如图1所示:
∵C是弧BD的中点,
∴∠DBC=∠BAC,
在ABC中,∠ACB=90°,CE⊥AB,
∴∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,
∴∠BCE=∠DBC,
∴CF=BF;
(2)解:连接OC交BD于G,如图2所示:
∵AB是O的直径,AB=2OC=10,
∴∠ADB=90°,
∴BD==8,
∵C是弧BD的中点,
∴OC⊥BD,DG=BG=BD=4,
∵OA=OB,
∴OG是△ABD的中位线,
∴OG=AD=3,
∴CG=OC-OG=5-3=2,
在Rt△BCG中,
由勾股定理得:BC=.
20.解:(1)如图1,
∵,
∴,
∴,
∵,
∴.
(2)依据题意画图.
连接BM,CM.
∵AB=AC,
∴,
∴,
∴BM=CM,∠BAM=∠CAM=20°,
∴∠MBC=∠CAM=20°,
∵BE⊥AC,AM⊥BC,
∴∠BGD=∠AFD=90°,
∴∠BDG=∠ADF=70°,
∵∠BMA=∠ACB=70°,
∴∠BMA=∠BDG=70°,
∴BD=BM,
又∵BG⊥DM,
∴GD=GM.即:G为DM的中点.
21.解:(1)连接OB,
∵∠OAB=α=35°,
∴∠OBA=35°,
∴∠AOB=110°,
∴β=∠AOB=55°;
(2)结论:α+β=90°.
证明:∵∠AOB=180°-2α,β=∠AOB
∴β=90°-α,
∴α+β=90°.
22.解:(1)BF=,
理由是:如图1,连接BG,CG,
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=(360°﹣∠BFE)=(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=FG.
故答案为:BF=FG;
(2)①如图2所示,
②;理由如下:
如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=FG,
∴DF=FG.
23.(1)解:∵BC为直径,
∴∠CDB=90°,
∴∠GDB=90°,
∴ ,
∵ ,
∴,
∵,
∴∠DBG=∠DBC=22.5°,
∴;
(2)证明:∵BC为直径,
∴∠CAB=90°,
∵,
∴∠ACB=45°,
∴∠F+∠CAF=∠ACB=45°,
∵∠CAF=∠DBC=22.5°,
∴∠CAF=22.5°,
∴∠F=∠CAF=22.5°,
∴CF=CA,
在 中,
∵,∠ACB=45°,
∴,
∴AC=BC,
由勾股定理得:AC2+AB2=2AC2=BC2,
∴ ,
∴,
∴;
(3)解:∵∠G=67.5°,,
∴∠BCG=67.5,
∴∠BCG=∠G,
∴BC=BG,
∴△BCG是等腰三角形,
∵∠BDC=90°,即BD⊥CG,
∴CD=DG,
∴ ,
在 中,∠CAB=90°,
∵,
∴∠ACB=∠ABC=45°,
∴AC=AB,
由勾股定理得:AC2+AB2=2AB2=BC2,
∴ ,
设⊙O的半径为r,则BG=BC=2r,,
∴ ,
∴四边形ABCD的面积等于
,
∵四边形ABCD的面积为,
∴ ,
解得: 或 (舍去)
即设⊙O的半径为
同课章节目录
