2021-2022学年人教版数学九年级上册 第二十四章 圆 单元测试 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册 第二十四章 圆 单元测试 (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览



文档简介
人教版数学九年级上册《第二十四章 圆》单元测试
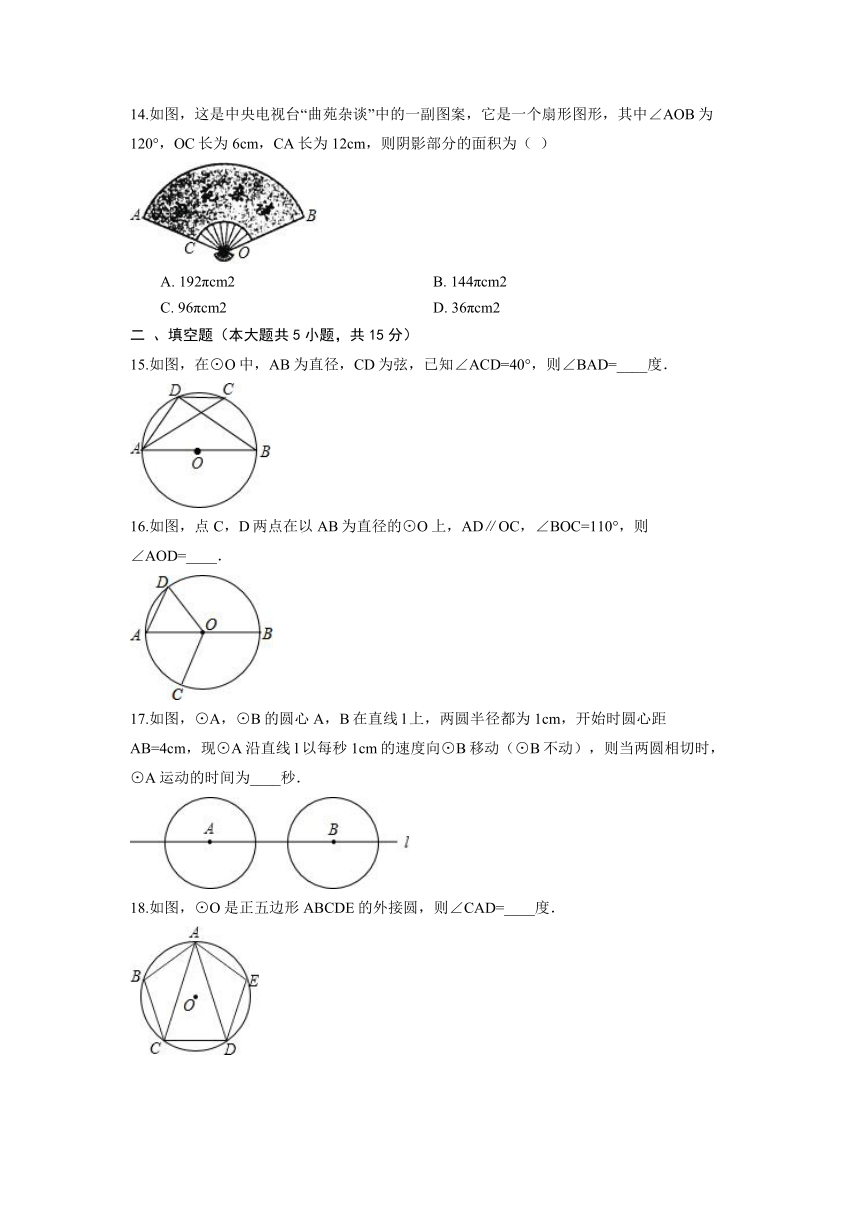
一 、单选题(本大题共14小题,共42分)
1.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB为( )
A. 34° B. 56° C. 60° D. 68°
2.下列说法中,正确的是( )
A. 长度相等的弧叫等弧 B. 直角所对的弦是直径
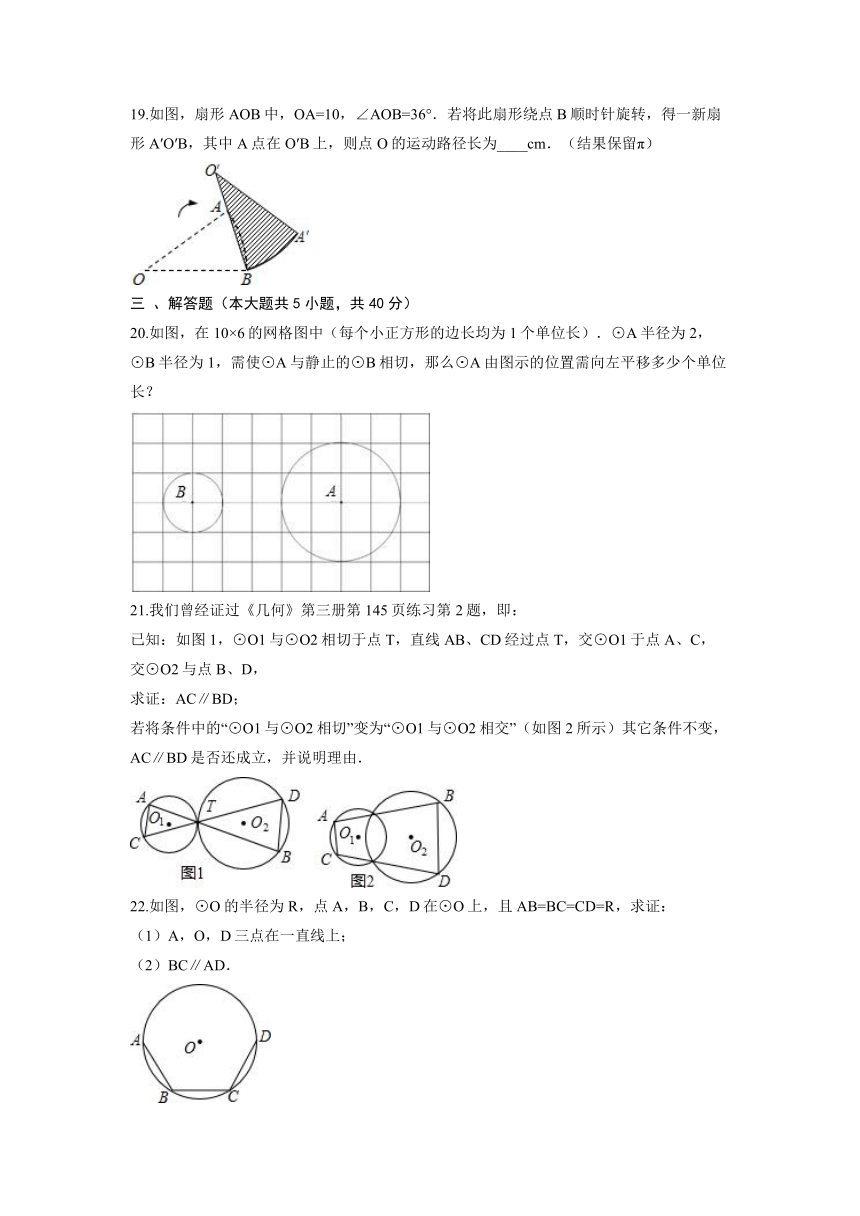
C. 同弦所对的圆周角相等 D. 等弧所对的弦相等
3.如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是( )
A. 40° B. 50° C. 60° D. 75°
4.如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
甲:以点A为圆心,AP长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:过点A作直线MN⊥OP:以点O为圆心,OP为半径画弧,交射线AM于点B,连接OB,交⊙O于点C,直线CP即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 两人都正确 D. 两人都错误
5.下列直线中,可以判定为圆的切线的是( )
A. 与圆仅有一个公共点的直线 B. 垂直于圆的半径的直线
C. 与圆心的距离等于直径的直线 D. 过圆的半径外端的直线
6.如图,△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D,DF⊥AC于F.给出以下五个结论:①BD=DC;②CF=EF;③弧AE=弧DE;④∠A=2∠FDC;⑤DF是⊙O的切线.其中正确的有( )
A. 5个 B. 4个 C. 3个 D. 2个
7.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )
A. 18° B. 27° C. 36° D. 54°
8.如图所示,△ABC是⊙O的内接正三角形,四边形DEFG是⊙O的内接正方形,EF∥BC,则∠AOF为( )
A. 125° B. 130° C. 135° D. 140°
9.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,
则∠AOQ=( )
A. 60° B. 65° C. 72° D. 75°
10.如图,多边形ABCDEFGH为⊙O的内接正八边形,图中箭头正好指向点A,当箭头绕着点O逆时针旋转270°时,箭头应正好指向( )
A. 点G B. 点E C. 点D D. 点C
11.如图,AOB是直角扇形,以OA、OB为直径在扇形中作圆,n与m分别表示两个阴影部分的面积,那么n、m的大小关系是( )
A. m=n B. m>n C. m<n D. 无法确定
12.如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
A. 2π B. 4π C. 6π D. 8π
13.如图,四边形ABCD是一个矩形,⊙C的半径是2cm,CF=4cm,EF=2cm.则图中阴影部分的面积约为(精确到0.1cm2)( )
A. 4.0cm2 B. 4.1cm2
C. 4.19cm2 D. 4.2cm2
14.如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一个扇形图形,其中∠AOB为120°,OC长为6cm,CA长为12cm,则阴影部分的面积为( )
A. 192πcm2 B. 144πcm2
C. 96πcm2 D. 36πcm2
二 、填空题(本大题共5小题,共15分)
15.如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=____度.
16.如图,点C,D两点在以AB为直径的⊙O上,AD∥OC,∠BOC=110°,则∠AOD=____.
17.如图,⊙A,⊙B的圆心A,B在直线l上,两圆半径都为1cm,开始时圆心距AB=4cm,现⊙A沿直线l以每秒1cm的速度向⊙B移动(⊙B不动),则当两圆相切时,⊙A运动的时间为____秒.
18.如图,⊙O是正五边形ABCDE的外接圆,则∠CAD=____度.
19.如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为____cm.(结果保留π)
三 、解答题(本大题共5小题,共40分)
20.如图,在10×6的网格图中(每个小正方形的边长均为1个单位长).⊙A半径为2,⊙B半径为1,需使⊙A与静止的⊙B相切,那么⊙A由图示的位置需向左平移多少个单位长?
21.我们曾经证过《几何》第三册第145页练习第2题,即:
已知:如图1,⊙O1与⊙O2相切于点T,直线AB、CD经过点T,交⊙O1于点A、C,交⊙O2与点B、D,
求证:AC∥BD;
若将条件中的“⊙O1与⊙O2相切”变为“⊙O1与⊙O2相交”(如图2所示)其它条件不变,AC∥BD是否还成立,并说明理由.
22.如图,⊙O的半径为R,点A,B,C,D在⊙O上,且AB=BC=CD=R,求证:
(1)A,O,D三点在一直线上;
(2)BC∥AD.
23.如图,边形ABCDE是⊙O的内接正五边形,求证:AE∥BD.
24.向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大?
答案和解析
1.【答案】D;
【解析】解:∵∠C=34°,
∴∠AOB=2∠C=68°.
故选D.
2.【答案】D;
【解析】解:A、能互相重合的弧是等弧,故选项错误;
B、90°的圆周角所对的弦是直径,故选项错误;
C、同弦所对的圆周角相等或互补,故选项错误;
D、正确.
故选D.
3.【答案】B;
【解析】解:连接AD,如图所示,
∵CD是直径,
∴∠CAD=90°,
∵∠D=∠B=40°,
∴∠ACD=90°-∠D=50°.
故选B.
4.【答案】C;
【解析】解:对于甲的作法:
连结OB,如图1,
∵OA=AP,
∴OP为⊙A的直径,
∴∠OBP=90°,
∴OB⊥PB,
∴PB为⊙O的切线,所以甲的说法正确;
对于乙的作法:
如图2,
∵MN⊥OP,
∴∠OAB=90°,
∵OA=AP,OB=OP,
∴OB=OP,
在△OAB和OCP中
OA=OC
∠AOB=∠COP
OB=OP
,
∴△OAB≌△OCP,
∴∠OAB=∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线,所以乙的说法正确.
故选C.
5.【答案】A;
【解析】解:A、根据圆的切线的定义,可知与圆仅有一个公共点的直线是切线,故选项正确;
B、垂直于圆的半径的直线,可能与圆相交或相离,故选项错误;
C、与圆心的距离等于直径的直线与圆相离,故选项错误;
D、过圆的半径外端的直线与圆相交或相切,故选项错误.
故选A.
6.【答案】B;
【解析】解:连接OD,AD.
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角),
∴AD⊥BC;
而在△ABC中,AB=AC,
∴AD是边BC上的中线,
∴BD=DC(正确);
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,
∵OA=OB,
∴OD是△ABC的中位线,
即:OD∥AC,
∵DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线(正确);
∵DF⊥AC,AD⊥BC,
∴∠FDC+∠C=∠CAD+∠C=90°,
∴∠FDC=∠CAD,
又AB=AC,∴∠BAD=∠CAD,
∴∠A=2∠CAD=2∠FDC(正确);
∵DF是⊙O的切线,
∴∠FDE=∠CAD=∠FDC,
∴∠C=∠DEC,
∴DC=DE,
又DF⊥AC,
∴CF=EF(正确);
当∠EAD=∠EDA时,AE=DE,此时△ABC为等边三角形,
当△ABC不是等边三角形时,
∠EAD≠∠EDA,
则AE≠DE,
∴AE=DE(不正确);
综上,正确结论的序号是①②④⑤,
故选:B.
7.【答案】B;
【解析】解:连接OB,
∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=36°,
∴∠AOB=180°-∠A-∠OBA=54°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C=
1
2
∠AOB=27°.
故选B.
8.【答案】C;
【解析】解:连接OG,
∵⊙O是△ABC的外接圆,
∴AO⊥EF,
∵EF∥BC,
∴AO⊥EF,
∵四边形DEFG是正方形,
∴DG∥EF,
∴AO⊥DG,
∴AO是DG的垂直平分线,
∴∠AOG=360°×
1
8
=45°,
∵四边形DEFG是正方形,
∴∠GOF=90°,
∴∠AOF=∠AOG+∠GOF=45°+90°=135°.
故选C.
9.【答案】D;
【解析】解:连接OD,AR,
∵△PQR是⊙O的内接正三角形,
∴∠PRQ=60°,
∴∠POQ=2×∠PRQ=120°,
∵四边形ABCD是⊙O的内接正方形,
∴△AOD为等腰直角三角形,
∴∠AOD=90°,
∵BC∥RQ,AD∥BC,
∴AD∥QR,
∴∠ARQ=∠DAR,
∴弧AQ=弧DR,
∵△PQR是等边三角形,
∴PQ=PR,
∴弧PQ=弧PR,
∴弧AP=弧PD,
∴∠AOP=
1
2
∠AOD=45°,
所以∠AOQ=∠POQ-∠AOP=120°-45°=75°.
故选D.
10.【答案】D;
【解析】解:正八边形的中心角是:
360
8
=45°,
270
45
=6,则箭头应正好指向C.
故选D.
11.【答案】A;
【解析】解:∵扇形OAB的圆心角为90°,假设扇形半径为a,
∴扇形面积为:
90π×a2
360
=
πa2
4
,
半圆面积为:
1
2
×π×(
a
2
)2=
πa2
8
,
∴Sn+SM =SM+Sm=
πa2
8
,
∴Sm=Sn,
即m与n面积的大小相等.
故选:A.
12.【答案】C;
【解析】解:∵∠ABC=30°,
∴∠AOC=60°,
∴S扇形AOC=
60π×62
360
=6π.
故选C.
13.【答案】D;
【解析】解:∵在Rt△CEF中,CF=4,EF=2,
∴∠C=30°,
又∵∠BCD=90°,⊙C的半径是2,
∴阴影部分面积为
(30+90) π 22
360
=
4π
3
≈4.2c.
故选D.
14.【答案】C;
【解析】解:OC=6,CA=12,则OA=18,
∴扇形OAB的面积=
120 π 182
360
=108π,
扇形OCD的面积=
120 π 62
360
=12π,
∴阴影部分的面积=108π-12π=96π(c).
故选C.
15.【答案】50;
【解析】解:∵在⊙O中,AB为直径,
∴∠ADB=90°,
∵∠B=∠ACD=40°,
∴∠BAD=90°-∠B=50°.
故答案为:50.
16.【答案】40°;
【解析】解:∵∠BOC=110°,∠BOC+∠AOC=180°,
∴∠AOC=70°,
∵AD∥OC,OD=OA,
∴∠D=∠A=∠AOC=70°,
∴∠AOD=180°-2∠A=40°.
故答案为40°
17.【答案】2或6;
【解析】解:本题所说的两圆相切,应分为两圆第一次相遇时的相切和两圆继续移动,即将相离时的相切两种情况.
第一种情况两圆所走的路程为4-2=2cm;
第二种情况两圆所走的路程为4+2=6cm.
不妨设圆A运动的时间为x秒,x=
2cm
1cm/s
=2s或
6cm
1cm/s
=6s,
解得x=2或6.
故答案为:2或6.
18.【答案】36;
【解析】解:根据正五边形的性质,可得AB=AE,BC=DE,∠B=∠E,∠BAE=108°,
∵在△ABC和△AED中
AB=AE
∠B=∠E
CB=DE
,
∴△ABC≌△AED(SAS),
∴∠CAB=∠DAE=
1
2
(180°-108°)=36°,
∴∠CAD=108°-36°-36°=36°.
故答案为:36.
19.【答案】4π;
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度=
72°×π×10
180°
=4πcm.
故答案是:4π.
20.【答案】解:当⊙A向左平移2、8个单位时两圆外切,
当⊙A向左平移4、6个单位时两圆内切,
故需向左平移2、4、6、8个单位中任一个.;
【解析】答题时考虑两圆内切还是外切两种情况,根据圆心距和半径之间的关系可以得到答案.
21.【答案】证明:(1)作两圆的内公切线MN.
则有∠ATM=∠C,∠BTN=∠D.
又∠AMT=∠BTN,
∴∠C=∠D.
∴AC∥BD.
(2)连接EF,则∠CFE=∠B,∠DFE=∠A.
又∠CFE+∠DFE=180°,
∴∠B+∠A=180°.
∴AC∥BD.;
【解析】(1)根据弦切角定理可以证明一对内错角相等,则得到平行;
(2)连接EF,根据圆内接四边形的对角互补,可以证明一对同旁内角互补,则两直线平行.
22.【答案】证明:(1)连接OA,OB,OC,OD,
∵OA=OB=OC=OD=R,
∴AB=BC=CD=OA=OB=OC=OD,
∴△OAB,△OBC,△OCD是等边三角形,
∴∠AOB=∠BOC=∠COD=60°,
∴∠AOB+∠BOC+∠COD=180°,
∴A,O,D三点在一直线上;
(2)∵△OAB,△OBC,△OCD是等边三角形,
∴∠AOB=60°,∠OBC=60°,
∴∠AOB=∠OBC,
∴BC∥AD.;
【解析】(1)连接OA,OB,OC,OD,证明△OAB,△OBC,△OCD是等边三角形,证得∠AOB+∠BOC+∠COD=180°,得出结论;
(2)证明∠AOB=∠OBC,利用平行线的判定定理可得结论.
23.【答案】证明:∵五边形ABCDE是正五边形,
∴∠A=∠C=∠ABC=∠EDC=108°,BC=CD,
∴∠CBD=∠CDB=(180°-∠E)÷2=(180°-108°)÷2=36°.
∴∠ABD=∠ABC-∠CBD=108°-36°=72°.
∵∠B+∠ABD=108°+72°=180°,
∴AE∥BD.;
【解析】根据多变形的内角和定理得出正五边形的内角和,根据正五边形的各内角相等,可得∠A的度数,根据三角形的内角和定理,可得∠CBD的度数,进而可得出∠ABD的度数,由此可得出结论.
24.【答案】解:第1,2,3个图形的面积为:4-π=(4-π);
第4个图形的面积为:4-2(4-π)=(2π-4);
∵(4-π)<(2π-4),
∴方案④种植月季花的面积最大.;
【解析】设正方形边长为2x,将第1个图形中的半圆的面积相加为以半径为x的圆;第2个图形为半径为x的圆的面积,第3个图形中4个扇形的面积相加为以半径为x的圆;故第1,2,3个图形阴影的面积为正方形的面积减去以x为半径的圆的面积;第4个图形的面积为正方形的面积减去空白面积,计算后比较即可.
一 、单选题(本大题共14小题,共42分)
1.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB为( )
A. 34° B. 56° C. 60° D. 68°
2.下列说法中,正确的是( )
A. 长度相等的弧叫等弧 B. 直角所对的弦是直径
C. 同弦所对的圆周角相等 D. 等弧所对的弦相等
3.如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是( )
A. 40° B. 50° C. 60° D. 75°
4.如图,P是⊙O外一点,OP交⊙O于点A,OA=AP.甲、乙两人想作一条通过点P与⊙O相切的直线,其作法如下.
甲:以点A为圆心,AP长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:过点A作直线MN⊥OP:以点O为圆心,OP为半径画弧,交射线AM于点B,连接OB,交⊙O于点C,直线CP即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 两人都正确 D. 两人都错误
5.下列直线中,可以判定为圆的切线的是( )
A. 与圆仅有一个公共点的直线 B. 垂直于圆的半径的直线
C. 与圆心的距离等于直径的直线 D. 过圆的半径外端的直线
6.如图,△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D,DF⊥AC于F.给出以下五个结论:①BD=DC;②CF=EF;③弧AE=弧DE;④∠A=2∠FDC;⑤DF是⊙O的切线.其中正确的有( )
A. 5个 B. 4个 C. 3个 D. 2个
7.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )
A. 18° B. 27° C. 36° D. 54°
8.如图所示,△ABC是⊙O的内接正三角形,四边形DEFG是⊙O的内接正方形,EF∥BC,则∠AOF为( )
A. 125° B. 130° C. 135° D. 140°
9.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,
则∠AOQ=( )
A. 60° B. 65° C. 72° D. 75°
10.如图,多边形ABCDEFGH为⊙O的内接正八边形,图中箭头正好指向点A,当箭头绕着点O逆时针旋转270°时,箭头应正好指向( )
A. 点G B. 点E C. 点D D. 点C
11.如图,AOB是直角扇形,以OA、OB为直径在扇形中作圆,n与m分别表示两个阴影部分的面积,那么n、m的大小关系是( )
A. m=n B. m>n C. m<n D. 无法确定
12.如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
A. 2π B. 4π C. 6π D. 8π
13.如图,四边形ABCD是一个矩形,⊙C的半径是2cm,CF=4cm,EF=2cm.则图中阴影部分的面积约为(精确到0.1cm2)( )
A. 4.0cm2 B. 4.1cm2
C. 4.19cm2 D. 4.2cm2
14.如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一个扇形图形,其中∠AOB为120°,OC长为6cm,CA长为12cm,则阴影部分的面积为( )
A. 192πcm2 B. 144πcm2
C. 96πcm2 D. 36πcm2
二 、填空题(本大题共5小题,共15分)
15.如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=____度.
16.如图,点C,D两点在以AB为直径的⊙O上,AD∥OC,∠BOC=110°,则∠AOD=____.
17.如图,⊙A,⊙B的圆心A,B在直线l上,两圆半径都为1cm,开始时圆心距AB=4cm,现⊙A沿直线l以每秒1cm的速度向⊙B移动(⊙B不动),则当两圆相切时,⊙A运动的时间为____秒.
18.如图,⊙O是正五边形ABCDE的外接圆,则∠CAD=____度.
19.如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为____cm.(结果保留π)
三 、解答题(本大题共5小题,共40分)
20.如图,在10×6的网格图中(每个小正方形的边长均为1个单位长).⊙A半径为2,⊙B半径为1,需使⊙A与静止的⊙B相切,那么⊙A由图示的位置需向左平移多少个单位长?
21.我们曾经证过《几何》第三册第145页练习第2题,即:
已知:如图1,⊙O1与⊙O2相切于点T,直线AB、CD经过点T,交⊙O1于点A、C,交⊙O2与点B、D,
求证:AC∥BD;
若将条件中的“⊙O1与⊙O2相切”变为“⊙O1与⊙O2相交”(如图2所示)其它条件不变,AC∥BD是否还成立,并说明理由.
22.如图,⊙O的半径为R,点A,B,C,D在⊙O上,且AB=BC=CD=R,求证:
(1)A,O,D三点在一直线上;
(2)BC∥AD.
23.如图,边形ABCDE是⊙O的内接正五边形,求证:AE∥BD.
24.向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大?
答案和解析
1.【答案】D;
【解析】解:∵∠C=34°,
∴∠AOB=2∠C=68°.
故选D.
2.【答案】D;
【解析】解:A、能互相重合的弧是等弧,故选项错误;
B、90°的圆周角所对的弦是直径,故选项错误;
C、同弦所对的圆周角相等或互补,故选项错误;
D、正确.
故选D.
3.【答案】B;
【解析】解:连接AD,如图所示,
∵CD是直径,
∴∠CAD=90°,
∵∠D=∠B=40°,
∴∠ACD=90°-∠D=50°.
故选B.
4.【答案】C;
【解析】解:对于甲的作法:
连结OB,如图1,
∵OA=AP,
∴OP为⊙A的直径,
∴∠OBP=90°,
∴OB⊥PB,
∴PB为⊙O的切线,所以甲的说法正确;
对于乙的作法:
如图2,
∵MN⊥OP,
∴∠OAB=90°,
∵OA=AP,OB=OP,
∴OB=OP,
在△OAB和OCP中
OA=OC
∠AOB=∠COP
OB=OP
,
∴△OAB≌△OCP,
∴∠OAB=∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线,所以乙的说法正确.
故选C.
5.【答案】A;
【解析】解:A、根据圆的切线的定义,可知与圆仅有一个公共点的直线是切线,故选项正确;
B、垂直于圆的半径的直线,可能与圆相交或相离,故选项错误;
C、与圆心的距离等于直径的直线与圆相离,故选项错误;
D、过圆的半径外端的直线与圆相交或相切,故选项错误.
故选A.
6.【答案】B;
【解析】解:连接OD,AD.
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角),
∴AD⊥BC;
而在△ABC中,AB=AC,
∴AD是边BC上的中线,
∴BD=DC(正确);
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴DB=DC,
∵OA=OB,
∴OD是△ABC的中位线,
即:OD∥AC,
∵DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线(正确);
∵DF⊥AC,AD⊥BC,
∴∠FDC+∠C=∠CAD+∠C=90°,
∴∠FDC=∠CAD,
又AB=AC,∴∠BAD=∠CAD,
∴∠A=2∠CAD=2∠FDC(正确);
∵DF是⊙O的切线,
∴∠FDE=∠CAD=∠FDC,
∴∠C=∠DEC,
∴DC=DE,
又DF⊥AC,
∴CF=EF(正确);
当∠EAD=∠EDA时,AE=DE,此时△ABC为等边三角形,
当△ABC不是等边三角形时,
∠EAD≠∠EDA,
则AE≠DE,
∴AE=DE(不正确);
综上,正确结论的序号是①②④⑤,
故选:B.
7.【答案】B;
【解析】解:连接OB,
∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=36°,
∴∠AOB=180°-∠A-∠OBA=54°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C=
1
2
∠AOB=27°.
故选B.
8.【答案】C;
【解析】解:连接OG,
∵⊙O是△ABC的外接圆,
∴AO⊥EF,
∵EF∥BC,
∴AO⊥EF,
∵四边形DEFG是正方形,
∴DG∥EF,
∴AO⊥DG,
∴AO是DG的垂直平分线,
∴∠AOG=360°×
1
8
=45°,
∵四边形DEFG是正方形,
∴∠GOF=90°,
∴∠AOF=∠AOG+∠GOF=45°+90°=135°.
故选C.
9.【答案】D;
【解析】解:连接OD,AR,
∵△PQR是⊙O的内接正三角形,
∴∠PRQ=60°,
∴∠POQ=2×∠PRQ=120°,
∵四边形ABCD是⊙O的内接正方形,
∴△AOD为等腰直角三角形,
∴∠AOD=90°,
∵BC∥RQ,AD∥BC,
∴AD∥QR,
∴∠ARQ=∠DAR,
∴弧AQ=弧DR,
∵△PQR是等边三角形,
∴PQ=PR,
∴弧PQ=弧PR,
∴弧AP=弧PD,
∴∠AOP=
1
2
∠AOD=45°,
所以∠AOQ=∠POQ-∠AOP=120°-45°=75°.
故选D.
10.【答案】D;
【解析】解:正八边形的中心角是:
360
8
=45°,
270
45
=6,则箭头应正好指向C.
故选D.
11.【答案】A;
【解析】解:∵扇形OAB的圆心角为90°,假设扇形半径为a,
∴扇形面积为:
90π×a2
360
=
πa2
4
,
半圆面积为:
1
2
×π×(
a
2
)2=
πa2
8
,
∴Sn+SM =SM+Sm=
πa2
8
,
∴Sm=Sn,
即m与n面积的大小相等.
故选:A.
12.【答案】C;
【解析】解:∵∠ABC=30°,
∴∠AOC=60°,
∴S扇形AOC=
60π×62
360
=6π.
故选C.
13.【答案】D;
【解析】解:∵在Rt△CEF中,CF=4,EF=2,
∴∠C=30°,
又∵∠BCD=90°,⊙C的半径是2,
∴阴影部分面积为
(30+90) π 22
360
=
4π
3
≈4.2c.
故选D.
14.【答案】C;
【解析】解:OC=6,CA=12,则OA=18,
∴扇形OAB的面积=
120 π 182
360
=108π,
扇形OCD的面积=
120 π 62
360
=12π,
∴阴影部分的面积=108π-12π=96π(c).
故选C.
15.【答案】50;
【解析】解:∵在⊙O中,AB为直径,
∴∠ADB=90°,
∵∠B=∠ACD=40°,
∴∠BAD=90°-∠B=50°.
故答案为:50.
16.【答案】40°;
【解析】解:∵∠BOC=110°,∠BOC+∠AOC=180°,
∴∠AOC=70°,
∵AD∥OC,OD=OA,
∴∠D=∠A=∠AOC=70°,
∴∠AOD=180°-2∠A=40°.
故答案为40°
17.【答案】2或6;
【解析】解:本题所说的两圆相切,应分为两圆第一次相遇时的相切和两圆继续移动,即将相离时的相切两种情况.
第一种情况两圆所走的路程为4-2=2cm;
第二种情况两圆所走的路程为4+2=6cm.
不妨设圆A运动的时间为x秒,x=
2cm
1cm/s
=2s或
6cm
1cm/s
=6s,
解得x=2或6.
故答案为:2或6.
18.【答案】36;
【解析】解:根据正五边形的性质,可得AB=AE,BC=DE,∠B=∠E,∠BAE=108°,
∵在△ABC和△AED中
AB=AE
∠B=∠E
CB=DE
,
∴△ABC≌△AED(SAS),
∴∠CAB=∠DAE=
1
2
(180°-108°)=36°,
∴∠CAD=108°-36°-36°=36°.
故答案为:36.
19.【答案】4π;
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度=
72°×π×10
180°
=4πcm.
故答案是:4π.
20.【答案】解:当⊙A向左平移2、8个单位时两圆外切,
当⊙A向左平移4、6个单位时两圆内切,
故需向左平移2、4、6、8个单位中任一个.;
【解析】答题时考虑两圆内切还是外切两种情况,根据圆心距和半径之间的关系可以得到答案.
21.【答案】证明:(1)作两圆的内公切线MN.
则有∠ATM=∠C,∠BTN=∠D.
又∠AMT=∠BTN,
∴∠C=∠D.
∴AC∥BD.
(2)连接EF,则∠CFE=∠B,∠DFE=∠A.
又∠CFE+∠DFE=180°,
∴∠B+∠A=180°.
∴AC∥BD.;
【解析】(1)根据弦切角定理可以证明一对内错角相等,则得到平行;
(2)连接EF,根据圆内接四边形的对角互补,可以证明一对同旁内角互补,则两直线平行.
22.【答案】证明:(1)连接OA,OB,OC,OD,
∵OA=OB=OC=OD=R,
∴AB=BC=CD=OA=OB=OC=OD,
∴△OAB,△OBC,△OCD是等边三角形,
∴∠AOB=∠BOC=∠COD=60°,
∴∠AOB+∠BOC+∠COD=180°,
∴A,O,D三点在一直线上;
(2)∵△OAB,△OBC,△OCD是等边三角形,
∴∠AOB=60°,∠OBC=60°,
∴∠AOB=∠OBC,
∴BC∥AD.;
【解析】(1)连接OA,OB,OC,OD,证明△OAB,△OBC,△OCD是等边三角形,证得∠AOB+∠BOC+∠COD=180°,得出结论;
(2)证明∠AOB=∠OBC,利用平行线的判定定理可得结论.
23.【答案】证明:∵五边形ABCDE是正五边形,
∴∠A=∠C=∠ABC=∠EDC=108°,BC=CD,
∴∠CBD=∠CDB=(180°-∠E)÷2=(180°-108°)÷2=36°.
∴∠ABD=∠ABC-∠CBD=108°-36°=72°.
∵∠B+∠ABD=108°+72°=180°,
∴AE∥BD.;
【解析】根据多变形的内角和定理得出正五边形的内角和,根据正五边形的各内角相等,可得∠A的度数,根据三角形的内角和定理,可得∠CBD的度数,进而可得出∠ABD的度数,由此可得出结论.
24.【答案】解:第1,2,3个图形的面积为:4-π=(4-π);
第4个图形的面积为:4-2(4-π)=(2π-4);
∵(4-π)<(2π-4),
∴方案④种植月季花的面积最大.;
【解析】设正方形边长为2x,将第1个图形中的半圆的面积相加为以半径为x的圆;第2个图形为半径为x的圆的面积,第3个图形中4个扇形的面积相加为以半径为x的圆;故第1,2,3个图形阴影的面积为正方形的面积减去以x为半径的圆的面积;第4个图形的面积为正方形的面积减去空白面积,计算后比较即可.
同课章节目录
