2021-2022学年北师大版数学九年级下册3.2圆的对称性课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册3.2圆的对称性课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 803.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 13:02:31 | ||
图片预览





文档简介
(共20张PPT)
北师大版数学九年级(下)
2.圆的对称性
第三章 圆
1
教学目标
重点难点
2.利用圆心角、弧、弦的对应关系解决问题。(难点)
2
1.认识圆的轴对称性、中心对称性,理解同圆或等圆中,圆心角、弧、弦的对应关系。(重点)
3
答一答
教学过程
温故知新
圆的定义是什么?
平面内由到定点的距离等于定长的所有点组成的图形。
圆的相关概念有哪些?
连接圆上任意两点间的线段叫做弦。
圆上任意两点间的部分叫做圆弧,简称弧。
议一议
教学过程
新课引入
4
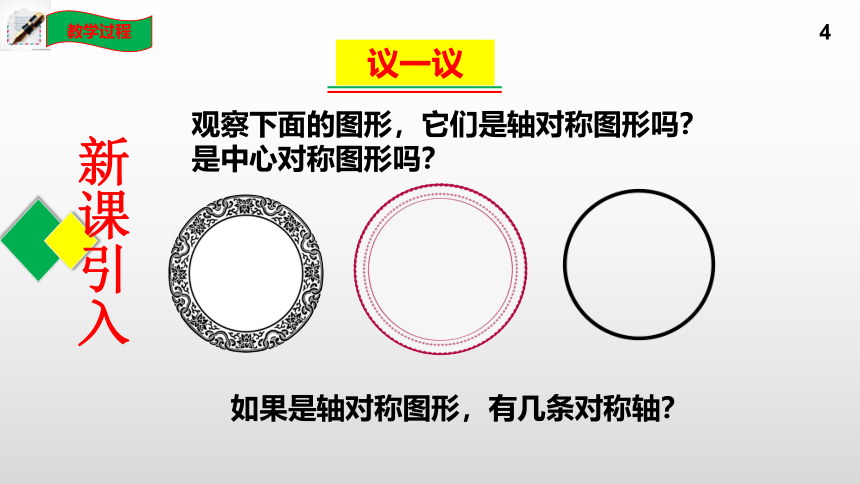
观察下面的图形,它们是轴对称图形吗?是中心对称图形吗?
如果是轴对称图形,有几条对称轴?
记一记
教学过程
新知新授
5
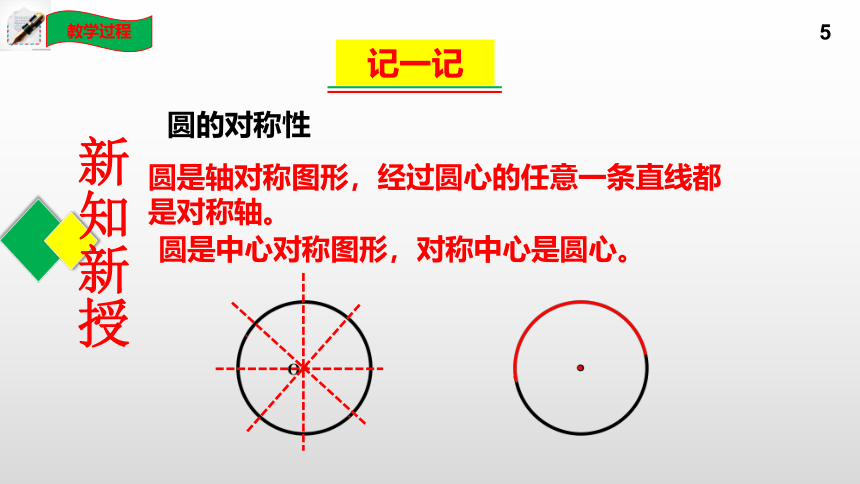
圆是轴对称图形,经过圆心的任意一条直线都是对称轴。
圆是中心对称图形,对称中心是圆心。
圆的对称性
做一做
教学过程
现学现用
6
1.圆是轴对称图形,它的对称轴是( )
A.直径 B.半径
C.半径所在的直线
D.经过直径上一点的直线
D
2.在圆画上合适的图案,使它变为既是轴对称图形又是中心对称图形。
记一记
教学过程
新知新授
7
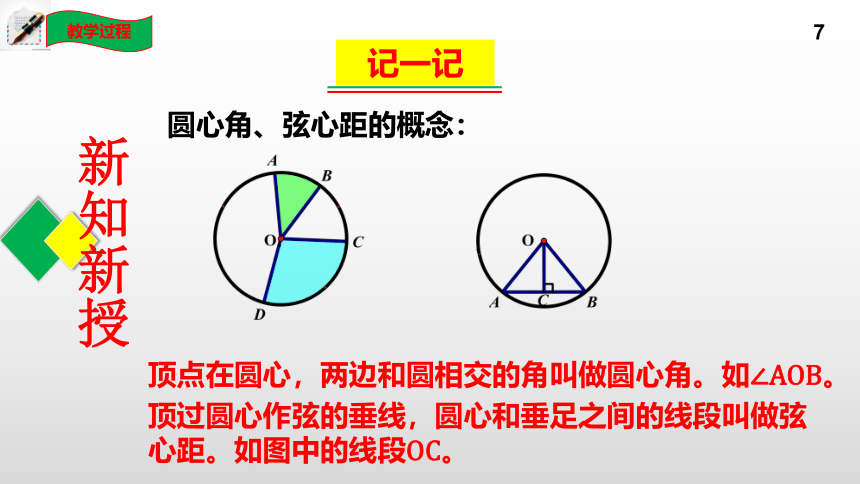
圆心角、弦心距的概念:
顶点在圆心,两边和圆相交的角叫做圆心角。如∠AOB。
顶过圆心作弦的垂线,圆心和垂足之间的线段叫做弦心距。如图中的线段OC。
议一议
教学过程
新知新授
8
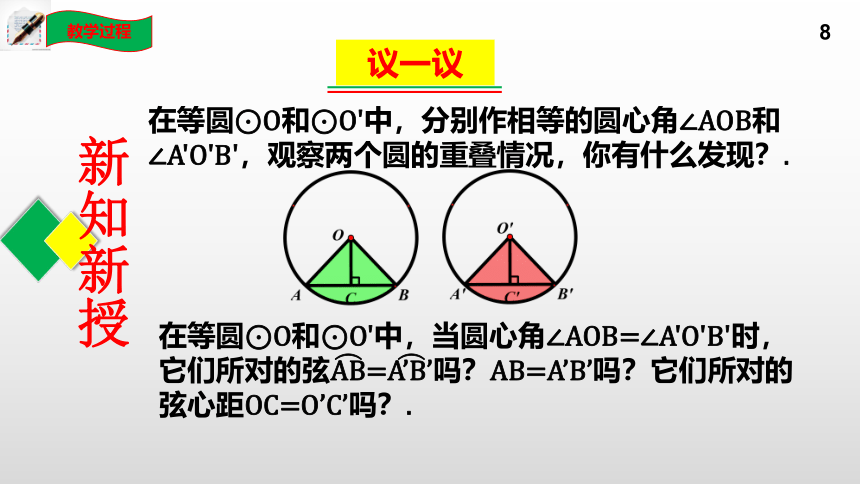
在等圆⊙O和⊙O'中,分别作相等的圆心角∠AOB和∠A'O'B',观察两个圆的重叠情况,你有什么发现?.
在等圆⊙O和⊙O'中,当圆心角∠AOB=∠A'O'B'时,它们所对的弦AB=A’B’吗?AB=A’B’吗?它们所对的弦心距OC=O’C’吗?.
⌒
⌒
记一记
教学过程
新知新授
9
通过上面的探究,我们可以得出同圆或等圆中圆心角、弧、弦、弦心距之间关系.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
注意:两个圆心角、两条弧、两条弦、两个弦心距相等的前提是“在同圆或等圆中”。
思考:在同圆或等圆中,两个圆心角、两条弧、两条弦、两个弦心距中任意一组量相等,其余的各组量也相等吗?
记一记
教学过程
新知新授
10
通过探究,我们进一步得出同圆或等圆中圆心角、弧、弦、弦心距之间关系.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等
记一记
教学过程
新知新授
11
同圆或等圆中圆心角、弧、弦、弦心距之间关系的符号表达:
在等圆⊙O和⊙O'中,∵∠AOB=∠A’O’B’
∴AB=A’B’, AB=A’B’, OC=O’C’
⌒
⌒
做一做
教学过程
现学现用
12
如图,在⊙O中,已知∠AOB=∠COD,则下面的关系式不正确的是( )
A. AC=BD
B. AC=BD
C. BC+BD> AB
D. S△ABC>S△DBC
⌒
⌒
D
做一做
教学过程
现学现用
13
4.如图,AB=2CD,则下列说法正确的是( )
A.AB=2CD
B.AB>2CD
C.AB<2CD
D.无法确定
⌒
⌒
C
做一做
教学过程
例题解析
14
例.如图所示,以 ABCD的顶点A为圆心,AB为半径画圆,与AD、BC相交于点E、F,延长BA交⊙A于点G,求证:EF=EG.
⌒
⌒
做一做
教学过程
例题解析
15
分析:根据圆心角、弧、弦之间的关系,要证明EF=EG,只需它们所对的圆心角相等,即要证明∠FAE=∠GAE,所以就需连结AF。再利用平行四边形的性质和平行线的性质即可得证.
⌒
⌒
做一做
教学过程
例题解析
16
证明:连结AF,
∵AB、AF为⊙A的半径,
∴AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠FAE,∠GAE=∠ABF,
∴∠FAE=∠GAE,
∴EF=EG.
⌒
⌒
做一做
教学过程
随堂练习
17
完成课本第72页“随堂练习”。
记一记
教学过程
课堂小结
18
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等
在等圆⊙O和⊙O'中,∵∠AOB=∠A’O’B’
∴AB=A’B’, AB=A’B’, OC=O’C’
⌒
⌒
做一做
教学过程
课后巩固
19
第一层:课本第72页习题3.2第1、2题
第一层:课本第72页习题3.2第1、2、3题
教学过程
结束新课
感谢聆听
20
北师大版数学九年级(下)
2.圆的对称性
第三章 圆
1
教学目标
重点难点
2.利用圆心角、弧、弦的对应关系解决问题。(难点)
2
1.认识圆的轴对称性、中心对称性,理解同圆或等圆中,圆心角、弧、弦的对应关系。(重点)
3
答一答
教学过程
温故知新
圆的定义是什么?
平面内由到定点的距离等于定长的所有点组成的图形。
圆的相关概念有哪些?
连接圆上任意两点间的线段叫做弦。
圆上任意两点间的部分叫做圆弧,简称弧。
议一议
教学过程
新课引入
4
观察下面的图形,它们是轴对称图形吗?是中心对称图形吗?
如果是轴对称图形,有几条对称轴?
记一记
教学过程
新知新授
5
圆是轴对称图形,经过圆心的任意一条直线都是对称轴。
圆是中心对称图形,对称中心是圆心。
圆的对称性
做一做
教学过程
现学现用
6
1.圆是轴对称图形,它的对称轴是( )
A.直径 B.半径
C.半径所在的直线
D.经过直径上一点的直线
D
2.在圆画上合适的图案,使它变为既是轴对称图形又是中心对称图形。
记一记
教学过程
新知新授
7
圆心角、弦心距的概念:
顶点在圆心,两边和圆相交的角叫做圆心角。如∠AOB。
顶过圆心作弦的垂线,圆心和垂足之间的线段叫做弦心距。如图中的线段OC。
议一议
教学过程
新知新授
8
在等圆⊙O和⊙O'中,分别作相等的圆心角∠AOB和∠A'O'B',观察两个圆的重叠情况,你有什么发现?.
在等圆⊙O和⊙O'中,当圆心角∠AOB=∠A'O'B'时,它们所对的弦AB=A’B’吗?AB=A’B’吗?它们所对的弦心距OC=O’C’吗?.
⌒
⌒
记一记
教学过程
新知新授
9
通过上面的探究,我们可以得出同圆或等圆中圆心角、弧、弦、弦心距之间关系.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
注意:两个圆心角、两条弧、两条弦、两个弦心距相等的前提是“在同圆或等圆中”。
思考:在同圆或等圆中,两个圆心角、两条弧、两条弦、两个弦心距中任意一组量相等,其余的各组量也相等吗?
记一记
教学过程
新知新授
10
通过探究,我们进一步得出同圆或等圆中圆心角、弧、弦、弦心距之间关系.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等
记一记
教学过程
新知新授
11
同圆或等圆中圆心角、弧、弦、弦心距之间关系的符号表达:
在等圆⊙O和⊙O'中,∵∠AOB=∠A’O’B’
∴AB=A’B’, AB=A’B’, OC=O’C’
⌒
⌒
做一做
教学过程
现学现用
12
如图,在⊙O中,已知∠AOB=∠COD,则下面的关系式不正确的是( )
A. AC=BD
B. AC=BD
C. BC+BD> AB
D. S△ABC>S△DBC
⌒
⌒
D
做一做
教学过程
现学现用
13
4.如图,AB=2CD,则下列说法正确的是( )
A.AB=2CD
B.AB>2CD
C.AB<2CD
D.无法确定
⌒
⌒
C
做一做
教学过程
例题解析
14
例.如图所示,以 ABCD的顶点A为圆心,AB为半径画圆,与AD、BC相交于点E、F,延长BA交⊙A于点G,求证:EF=EG.
⌒
⌒
做一做
教学过程
例题解析
15
分析:根据圆心角、弧、弦之间的关系,要证明EF=EG,只需它们所对的圆心角相等,即要证明∠FAE=∠GAE,所以就需连结AF。再利用平行四边形的性质和平行线的性质即可得证.
⌒
⌒
做一做
教学过程
例题解析
16
证明:连结AF,
∵AB、AF为⊙A的半径,
∴AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠FAE,∠GAE=∠ABF,
∴∠FAE=∠GAE,
∴EF=EG.
⌒
⌒
做一做
教学过程
随堂练习
17
完成课本第72页“随堂练习”。
记一记
教学过程
课堂小结
18
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等
在等圆⊙O和⊙O'中,∵∠AOB=∠A’O’B’
∴AB=A’B’, AB=A’B’, OC=O’C’
⌒
⌒
做一做
教学过程
课后巩固
19
第一层:课本第72页习题3.2第1、2题
第一层:课本第72页习题3.2第1、2、3题
教学过程
结束新课
感谢聆听
20
