2021-2022学年人教版数学八年级上册15.3分式方程与实际问题课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册15.3分式方程与实际问题课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 13:03:50 | ||
图片预览



文档简介
(共17张PPT)
分式方程与实际问题
复习巩固
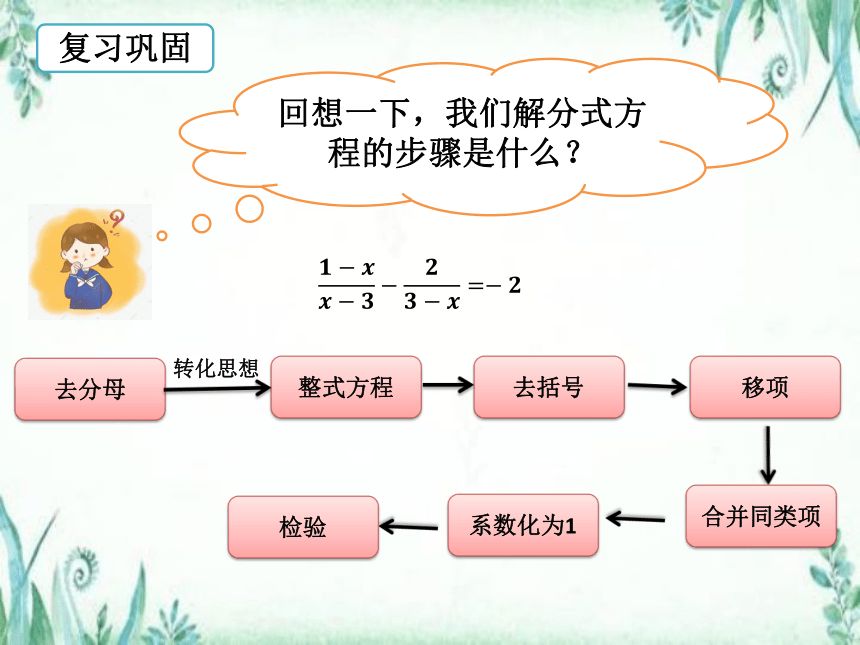
去括号
移项
整式方程
去分母
回想一下,我们解分式方程的步骤是什么?
合并同类项
系数化为1
检验
转化思想
引入新课
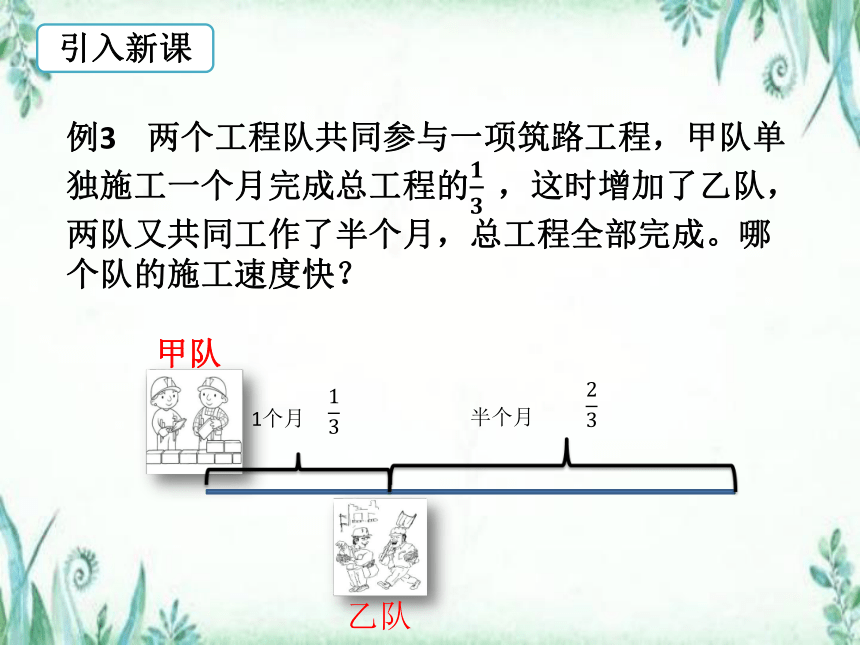
例3 两个工程队共同参与一项筑路工程,甲队单独施工一个月完成总工程的,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
甲队
乙队
1个月
半个月
我每次能吃这个苹果的
我每次能吃这个苹果的
谁能够最快吃完这个苹果呢?
小明
小红
谁的工作效率高,谁完成这项工程就快
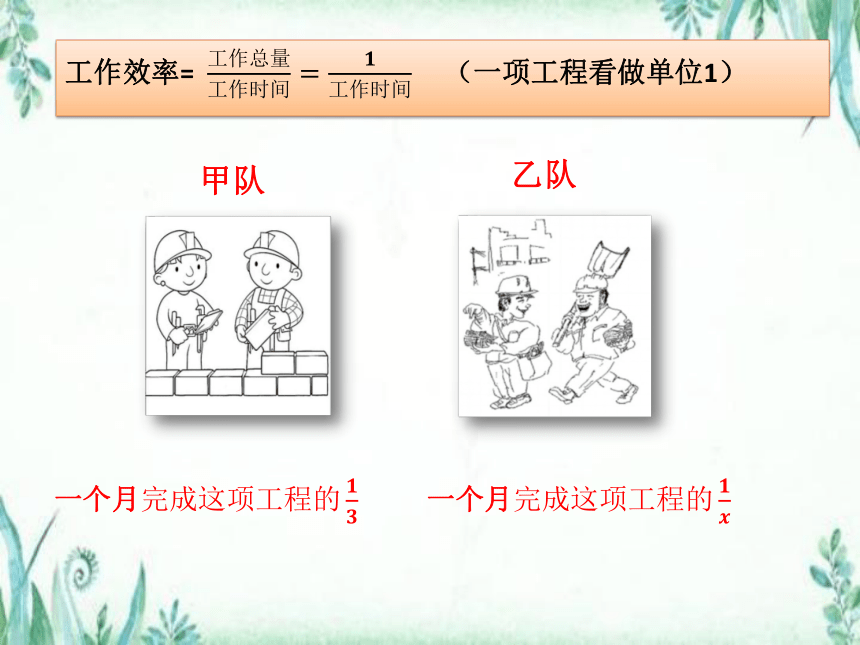
甲队
乙队
工作效率= (一项工程看做单位1)
一个月
一个月
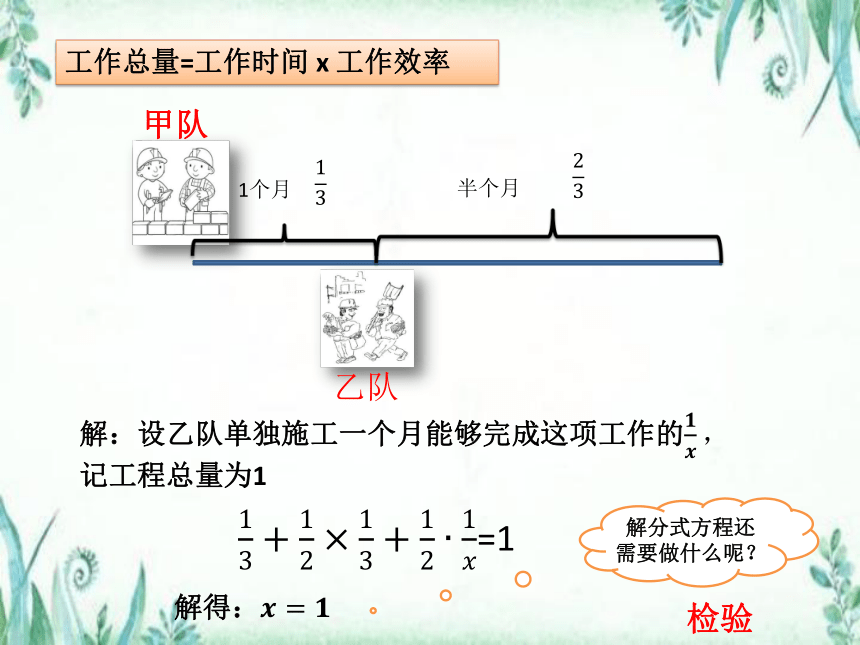
工作总量=工作时间 x 工作效率
甲队
乙队
1个月
半个月
解:设乙队单独施工一个月能够完成这项工作的记工程总量为1
=1
解得:
解分式方程还需要做什么呢?
检验
解:设乙队单独施工一个月能够完成这项工作的记工程总量为1
=1
解得:
方程
检验:当
所以
乙队的施工速度快
用分式方程来解决实际问题时,要注意解题过程!特别注意检验!
例4 某次列车平均提速v km/h ,用相同的时间,列车提前行驶s km,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
时间=
解:设提速前的平均速度为x km/h
提速前的时间=
提速后的时间=
根据
解:设提速前的平均速度为x km/h
解得:
方程
检验:,当
所以
答:提速前的平均速度为x=
要记得检验哟!
归纳总结
用分式方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
分式方程
设未知数,列分式方程
解方程
分式方程的解(x = a)
实际问题的答案
检 验
巩固新课
1、八年级学生去距学校10km 的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度
10 km
分析:设骑车学生的速度为x km/h ,则汽车的速度为2x km/h
时间=
则骑车学生到达博物馆的时间为:
则乘汽车学生到达博物馆的时间为:
骑自行车的学生先走20分钟后,乘汽车的学生再走,然后同时到达博物馆,意味着:
骑自行车的学生所花的时间比乘汽车的学生多花20分钟
解得:
方程
6
检验:当
所以
答:骑自行车的学生的速度为15km/h
时间=
解:设骑车学生的速度为x km/h ,则汽车的速度为2x km/h
2、 甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,求甲、乙每小时各做多少零件?
解得:
方程
检验:当
所以
答:甲每小时做15个,乙每小时做18个
解:设乙每小时做x个零件,则甲每小时做x+6个零件
课堂小结
今天我们主要学习了什么呢?
1、利用分式方程去解决实际问题
2、根据题意列出分式方程,并能够解分式方程,体会数学与实际生活的联系。
用分式方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
分式方程
设未知数,列分式方程
解方程
分式方程的解(x = a)
实际问题的答案
检 验
工作效率=
工作时间=
工作总量=工作时间 x 工作效率
时间=
速度=
路程=时间 x 速度
1、工程类问题
2、路程类问题
想要学得好,公式要记牢
分式方程与实际问题
复习巩固
去括号
移项
整式方程
去分母
回想一下,我们解分式方程的步骤是什么?
合并同类项
系数化为1
检验
转化思想
引入新课
例3 两个工程队共同参与一项筑路工程,甲队单独施工一个月完成总工程的,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
甲队
乙队
1个月
半个月
我每次能吃这个苹果的
我每次能吃这个苹果的
谁能够最快吃完这个苹果呢?
小明
小红
谁的工作效率高,谁完成这项工程就快
甲队
乙队
工作效率= (一项工程看做单位1)
一个月
一个月
工作总量=工作时间 x 工作效率
甲队
乙队
1个月
半个月
解:设乙队单独施工一个月能够完成这项工作的记工程总量为1
=1
解得:
解分式方程还需要做什么呢?
检验
解:设乙队单独施工一个月能够完成这项工作的记工程总量为1
=1
解得:
方程
检验:当
所以
乙队的施工速度快
用分式方程来解决实际问题时,要注意解题过程!特别注意检验!
例4 某次列车平均提速v km/h ,用相同的时间,列车提前行驶s km,提速后比提速前多行驶50km,提速前列车的平均速度为多少?
时间=
解:设提速前的平均速度为x km/h
提速前的时间=
提速后的时间=
根据
解:设提速前的平均速度为x km/h
解得:
方程
检验:,当
所以
答:提速前的平均速度为x=
要记得检验哟!
归纳总结
用分式方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
分式方程
设未知数,列分式方程
解方程
分式方程的解(x = a)
实际问题的答案
检 验
巩固新课
1、八年级学生去距学校10km 的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度
10 km
分析:设骑车学生的速度为x km/h ,则汽车的速度为2x km/h
时间=
则骑车学生到达博物馆的时间为:
则乘汽车学生到达博物馆的时间为:
骑自行车的学生先走20分钟后,乘汽车的学生再走,然后同时到达博物馆,意味着:
骑自行车的学生所花的时间比乘汽车的学生多花20分钟
解得:
方程
6
检验:当
所以
答:骑自行车的学生的速度为15km/h
时间=
解:设骑车学生的速度为x km/h ,则汽车的速度为2x km/h
2、 甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,求甲、乙每小时各做多少零件?
解得:
方程
检验:当
所以
答:甲每小时做15个,乙每小时做18个
解:设乙每小时做x个零件,则甲每小时做x+6个零件
课堂小结
今天我们主要学习了什么呢?
1、利用分式方程去解决实际问题
2、根据题意列出分式方程,并能够解分式方程,体会数学与实际生活的联系。
用分式方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
分式方程
设未知数,列分式方程
解方程
分式方程的解(x = a)
实际问题的答案
检 验
工作效率=
工作时间=
工作总量=工作时间 x 工作效率
时间=
速度=
路程=时间 x 速度
1、工程类问题
2、路程类问题
想要学得好,公式要记牢
