高二（秋）半期试题(无答）

高二（秋）半期试题
（考试时间：120分钟）
第Ⅰ卷(选择题、填空题共76分)
一、选择题（每小题5分，共60分）
1.在中,,则( )
A、 B、 C、 D、
2、两灯塔，与海洋观察站的距离都等于, 灯塔在C北偏东, 在南偏东，则,之间的相距（ ）
A． B． C． D．
3、已知数列为等差数列，且，则的值为
A． B． C． D．
4、数列中，=15，（），则该数列中相邻两项的乘积是负数的是（ ）
A． B． C． D．
5、在首项为21，公比为的等比数列中，最接近1的项是（ ）
A．第三项 B．第四项 C．第五项 D．第六项
6、已知,则下列推证中正确的是( )
A． B　
C、 D
7．如果，那么的最小值是（ ）
A．4 B． C．9 D．18
8、若不等式和不等式的解集相同，则、的值为（ ）
A．=﹣8 =﹣10 B．=﹣4 =﹣9 C．=﹣1 =9 D．=﹣1 =2
9、在△ABC中，角A、B、C所对的边分别是a、b、c，a＝1，b＝，A＝30°，则c的值为（ ）。
A、2 B、1 C、1或2 D、或2
10、若等差数列、前项和分别为、，且，则（ ）
A． B． C． D．
11、已知钝角△ABC的最长边为2，其余两边的长为、，则集合所表示的平面图形面积等于（ ）
A．2 B． C．4 D．
12、( )
A． B． C、 D、


题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题（每小题4分，共16分）
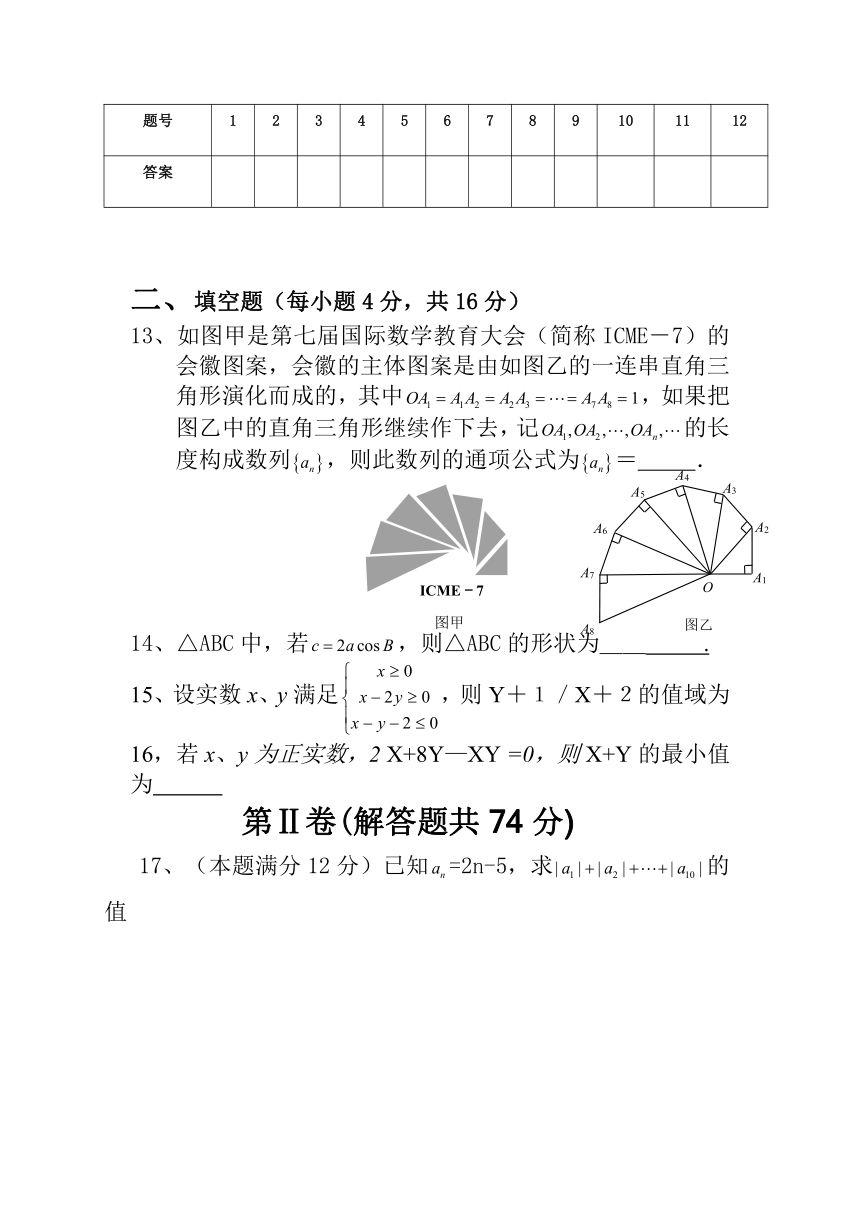
13、如图甲是第七届国际数学教育大会（简称ICME－7）的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中，如果把图乙中的直角三角形继续作下去，记的长度构成数列，则此数列的通项公式为＝ ．


14、△ABC中，若，则△ABC的形状为＿＿ .
15、设实数x、y满足，则Y＋１／X＋２的值域为
16，若x、y为正实数，2 X+8Y—XY =0，则X+Y的最小值为
第Ⅱ卷(解答题共74分)
17、（本题满分12分）已知=2n-5，求的值
18（本题满分12分）
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米。
（1）若设休闲区的长米，求公园ABCD所占面积S关于的函数的解析式；
（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？
19、（本题满分12分）
在中，为角所对的三边，已知．
（Ⅰ）求角的值；（Ⅱ）若，，求的长.
20（本题满分12分）
. (本小题满分14分)某工厂用两种不同的原料均可提炼同一种金属铝，若采用原料A，则原料成本为500元/吨，运费为500元/吨，可生产铝5 kg/t；若采用原料B，则原料成本为1500元/吨，运费400元/吨，可生产铝10 kg/t。若每日预算原料总成本不得超过6000元，运费不得超过2000元，则此工厂每日最多可生产多少千克铝。
21、（本题满分12分）
已知函数，且，，，…，构成数列，
又。（1）求数列的通项公式；（2）求证：．
22、（本题满分14分）
设数列的前项和为,
(1)若,求;
(2)若,求的前6项和;
(3)若,证明是等差数列.