人教版数学七年级上册1.4.2 有理数的除法3 课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.4.2 有理数的除法3 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 594.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 13:07:50 | ||
图片预览






文档简介
(共26张PPT)
某周每天上午8时的气温记录如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
-3℃ -2℃ -3℃ 0℃ -2℃ -1℃ -3℃
如何求这周每天上午8时的平均气温?
即 (-14)÷7
学习目标:
1、会将有理数的除法转化为乘法。
2、能熟练的进行有理数乘除混合运算。
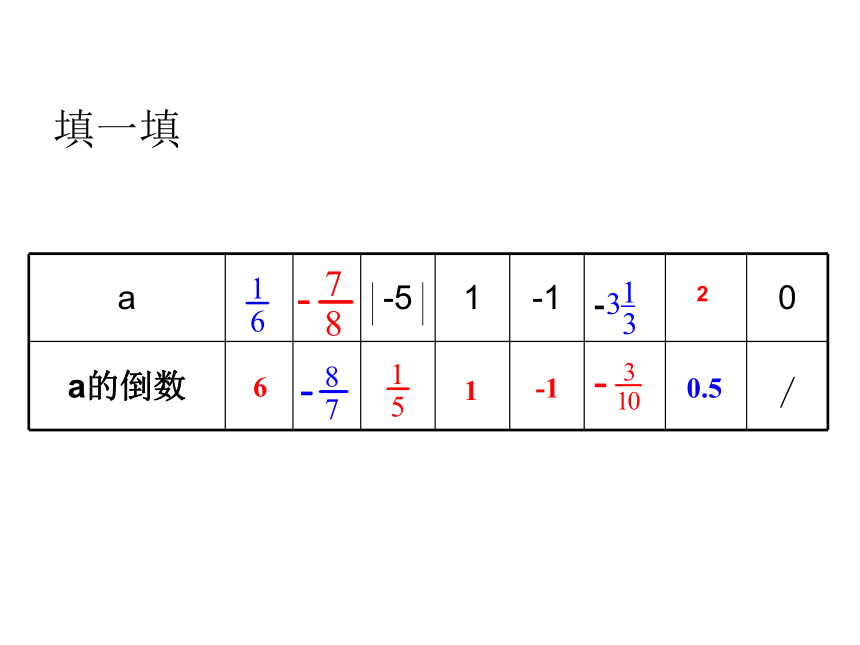
填一填
a -5 1 -1 0
a的倒数
6
1
-1
/
0.5
2
1、(-2) ×7=___
-14
除法是乘法的逆运算
(-14)÷7=___
-2
-2
2、(-2)×(-4)=___
8
8÷ (-4)=___
-2
-2
-2
★
★
◆
◆
合作探究
小组合作,比较大小.
=
=
=
通过这三个式子的大小比较,你有什么发现吗
除法可以转化为乘法
(1)除号变为乘号
(2)除数变为它的倒数
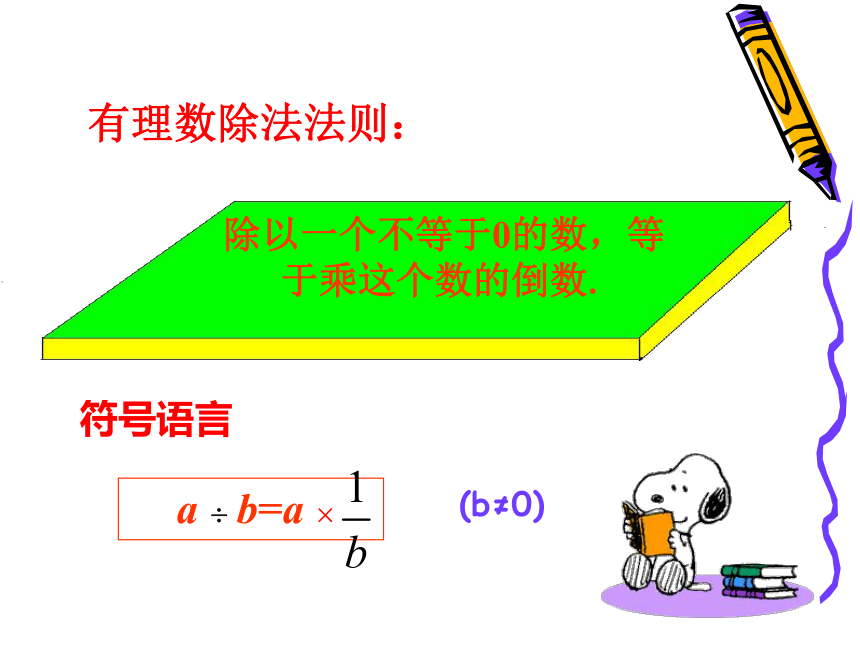
除以一个不等于0的数,等于乘这个数的倒数.
有理数除法法则:
a ÷ b=a ×
(b≠0)
符号语言
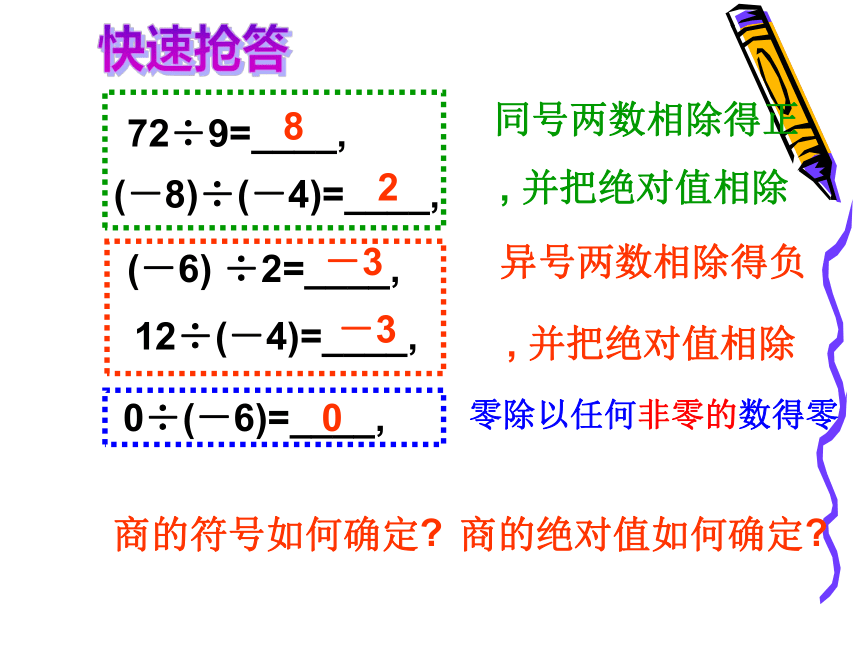
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-8)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
商的符号如何确定
商的绝对值如何确定
异号两数相除得负
, 并把绝对值相除
同号两数相除得正
, 并把绝对值相除
零除以任何非零的数得零
2
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何不等于0数都得_____.
正
负
相除
0
0不能作为除数
例1: 计算: (1) (-36) ÷9
(2) ( ) ÷( )
=
× ( )
=
解: (1) (-36) ÷9 =-(36÷9) =-4
(2) ( )
÷
合作交流
能整除时,将商的符号确定后,直接将绝对值相除
不能整除时,将除数变为它的倒数,再用乘法
两个有理数相除,有两种方法:
第一种运用有理数的除法法则:两数相除,同号得正,异号得负,并把绝对值相除;
第二种方法是把除法转化为乘法:除以一个数等于乘以这个数的倒数;(0不能作除数)
如(-78) ÷3运用上述第______种方法简便.
用上述______种方法比较简便.
一
二
1、计算:
(-18) ÷3 (2) (-63) ÷(-9)
(3) 1 ÷(-9) (4)0÷(-8)
2、35页练习
两数相除,同号得 ,异号得 ,并
把绝对值相 ,0除以任何一个不等于0
的数,都得 .
正
负
除
0
两数相除的符号法则:
计算:
计算:
计算:
计算:
计算:
例3 化简下列分数:
(1) (2)
分数可以理解为分子除以分母.
(1) =(-12) ÷3=-4
=(-45) ÷(-12)
=45÷12
=
解:
例3,计算:
1除以一个不为零的数的商就是这个数的倒数.
解:
(1)
(2)
解:
1.有理数的除法法则(一)
除以一个不等于零的数等于乘这个数的倒数.
a÷b=a× (b≠0).
2.有理数除法法则(二)同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除.
0除以任何一个不等于0的数都得0.
1、填空题
(1)(-27)÷3=___,
(-27)÷(-3)=___
(2)6÷(-0.3)=___,
___÷(-0.32)=0
(3)1÷
=_ ,
=_
分层训练
-9
9
-20
0
2、 两个有理数的商为正数,和为负数,这两个数的符号是( )
A.一正一负 B.都是负数
C.都是正数 D.不能确定
分层训练
B
变式:若 >0,a+b>0,则( )
A、a>0,b>0 B、a>0,b<0
C、a<0,b>0 D、a<0,b<0
A
3、下列说法中错误的是 ( )
A.互为倒数的两个数同号;
B.零没有倒数;
C.零没有相反数;
D.零除以任意非零数商为0
C
B
4、下面说法不正确的是 ( )
A.一个数与它倒数之积是1
B.一个数与它相反数之商是-1
C.两个数的商为-1,这两个数互为相反数
D.两个数的积为1,这两个数互为倒数
分层训练
挑战自我
1
-1
-2,0,2
1、已知:︱a︱=3, ︱b︱=2且 <0
求 3a-2b 的值.
2、若x<0,则 =
3、已知a、b互为相反数,c、d互为倒
数,且a≠0,那么
的值是多少?
-1
某周每天上午8时的气温记录如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
-3℃ -2℃ -3℃ 0℃ -2℃ -1℃ -3℃
如何求这周每天上午8时的平均气温?
即 (-14)÷7
学习目标:
1、会将有理数的除法转化为乘法。
2、能熟练的进行有理数乘除混合运算。
填一填
a -5 1 -1 0
a的倒数
6
1
-1
/
0.5
2
1、(-2) ×7=___
-14
除法是乘法的逆运算
(-14)÷7=___
-2
-2
2、(-2)×(-4)=___
8
8÷ (-4)=___
-2
-2
-2
★
★
◆
◆
合作探究
小组合作,比较大小.
=
=
=
通过这三个式子的大小比较,你有什么发现吗
除法可以转化为乘法
(1)除号变为乘号
(2)除数变为它的倒数
除以一个不等于0的数,等于乘这个数的倒数.
有理数除法法则:
a ÷ b=a ×
(b≠0)
符号语言
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-8)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
商的符号如何确定
商的绝对值如何确定
异号两数相除得负
, 并把绝对值相除
同号两数相除得正
, 并把绝对值相除
零除以任何非零的数得零
2
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何不等于0数都得_____.
正
负
相除
0
0不能作为除数
例1: 计算: (1) (-36) ÷9
(2) ( ) ÷( )
=
× ( )
=
解: (1) (-36) ÷9 =-(36÷9) =-4
(2) ( )
÷
合作交流
能整除时,将商的符号确定后,直接将绝对值相除
不能整除时,将除数变为它的倒数,再用乘法
两个有理数相除,有两种方法:
第一种运用有理数的除法法则:两数相除,同号得正,异号得负,并把绝对值相除;
第二种方法是把除法转化为乘法:除以一个数等于乘以这个数的倒数;(0不能作除数)
如(-78) ÷3运用上述第______种方法简便.
用上述______种方法比较简便.
一
二
1、计算:
(-18) ÷3 (2) (-63) ÷(-9)
(3) 1 ÷(-9) (4)0÷(-8)
2、35页练习
两数相除,同号得 ,异号得 ,并
把绝对值相 ,0除以任何一个不等于0
的数,都得 .
正
负
除
0
两数相除的符号法则:
计算:
计算:
计算:
计算:
计算:
例3 化简下列分数:
(1) (2)
分数可以理解为分子除以分母.
(1) =(-12) ÷3=-4
=(-45) ÷(-12)
=45÷12
=
解:
例3,计算:
1除以一个不为零的数的商就是这个数的倒数.
解:
(1)
(2)
解:
1.有理数的除法法则(一)
除以一个不等于零的数等于乘这个数的倒数.
a÷b=a× (b≠0).
2.有理数除法法则(二)同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除.
0除以任何一个不等于0的数都得0.
1、填空题
(1)(-27)÷3=___,
(-27)÷(-3)=___
(2)6÷(-0.3)=___,
___÷(-0.32)=0
(3)1÷
=_ ,
=_
分层训练
-9
9
-20
0
2、 两个有理数的商为正数,和为负数,这两个数的符号是( )
A.一正一负 B.都是负数
C.都是正数 D.不能确定
分层训练
B
变式:若 >0,a+b>0,则( )
A、a>0,b>0 B、a>0,b<0
C、a<0,b>0 D、a<0,b<0
A
3、下列说法中错误的是 ( )
A.互为倒数的两个数同号;
B.零没有倒数;
C.零没有相反数;
D.零除以任意非零数商为0
C
B
4、下面说法不正确的是 ( )
A.一个数与它倒数之积是1
B.一个数与它相反数之商是-1
C.两个数的商为-1,这两个数互为相反数
D.两个数的积为1,这两个数互为倒数
分层训练
挑战自我
1
-1
-2,0,2
1、已知:︱a︱=3, ︱b︱=2且 <0
求 3a-2b 的值.
2、若x<0,则 =
3、已知a、b互为相反数,c、d互为倒
数,且a≠0,那么
的值是多少?
-1
