华东师大版八年级数学上册 13.3.1 等腰三角形的性质课件(20张ppt)
文档属性
| 名称 | 华东师大版八年级数学上册 13.3.1 等腰三角形的性质课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 174.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
等腰三角形的性质
Contents
目录
01
02
03
04
牛刀小试
例题演示
新知探究
新课导入
05
深入探究
课堂小结
06
等腰三角形
一.基本概念
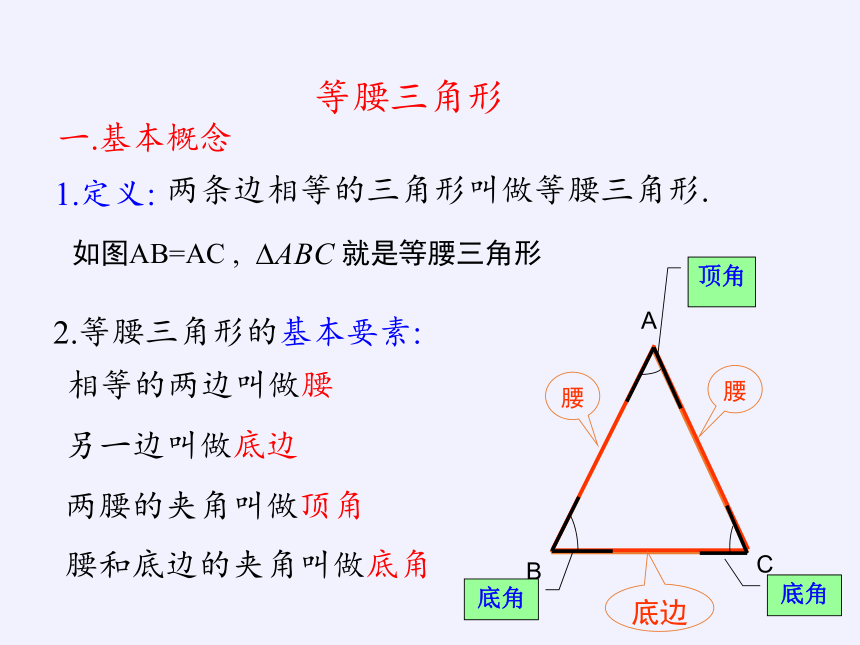
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC , 就是等腰三角形
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
C
A
B
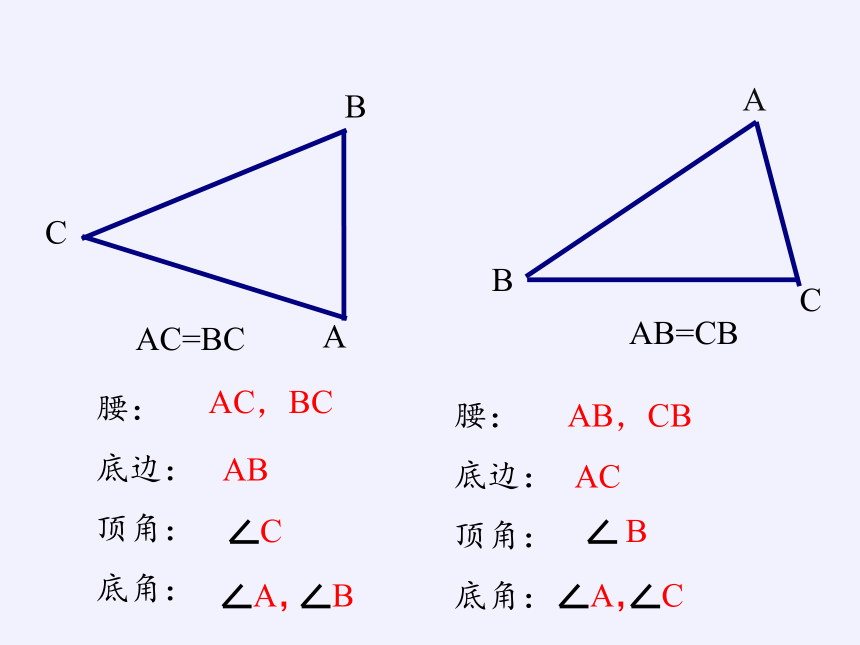
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
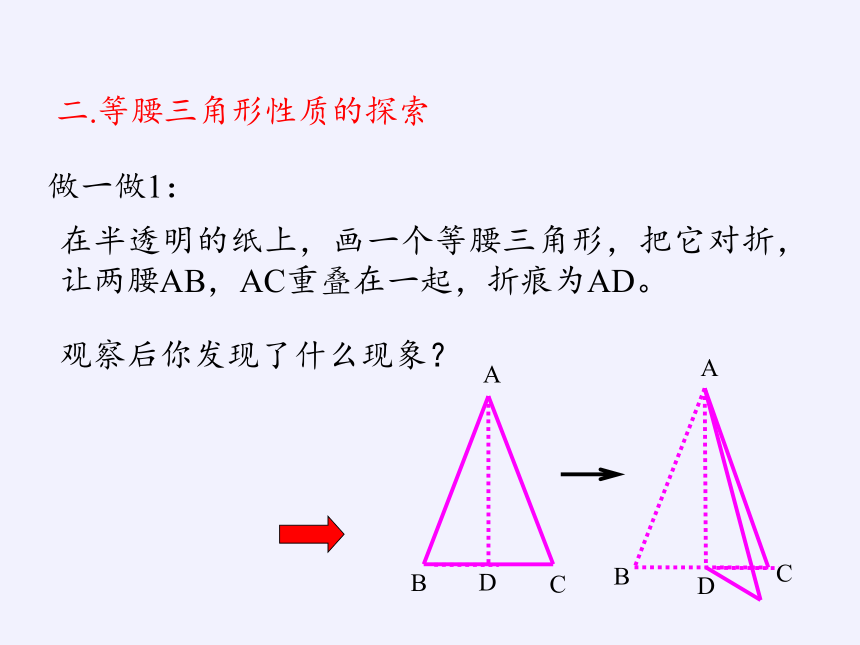
做一做1:
在半透明的纸上,画一个等腰三角形,把它对折,让两腰AB,AC重叠在一起,折痕为AD。
观察后你发现了什么现象?
二.等腰三角形性质的探索
B
A
C
D
A
B
C
D
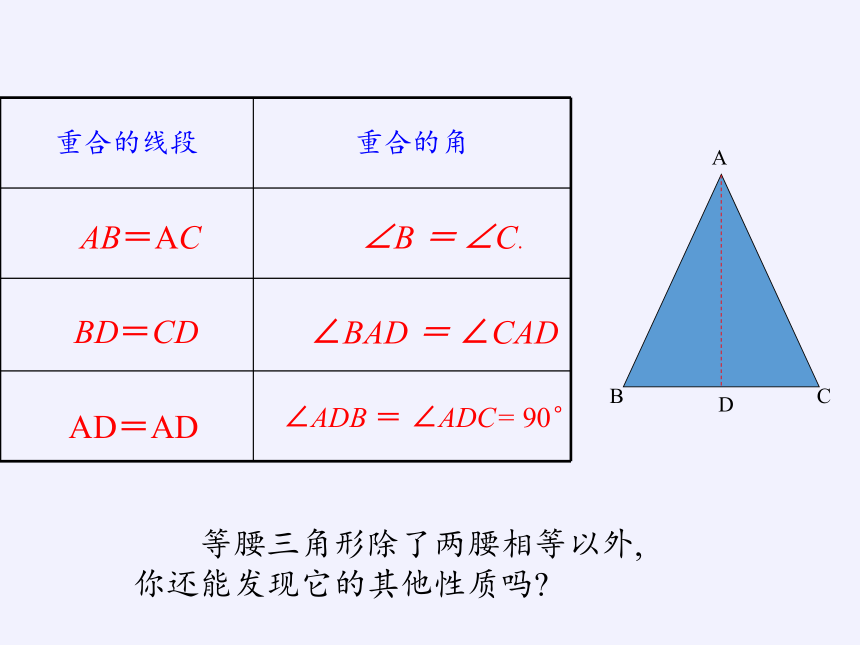
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗
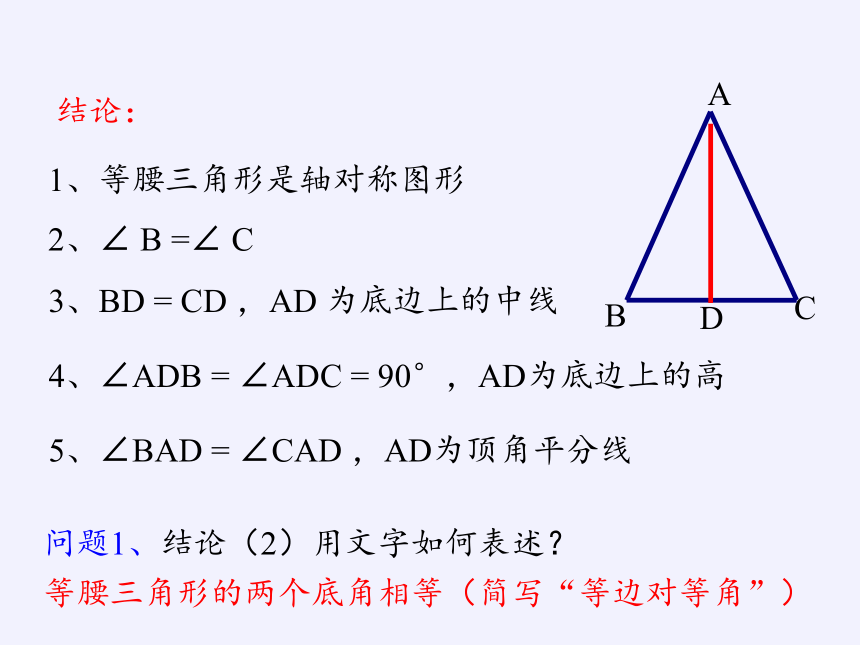
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD ,AD为顶角平分线
问题1、结论(2)用文字如何表述?
等腰三角形的两个底角相等(简写“等边对等角”)
C
A
B
D
结论:
C
A
B
D
如何证明:等腰三角形的两个底角相等?
已知:如图△ABC中,AB=AC.
求证:∠B=∠C.
证明:过A作AD⊥BC于D
∟
在Rt△ABD和Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ABD≌Rt△ACD(H.L.)
∴∠B=∠C(全等三角形的对应角相等)
思考1:还有其他的证明方法吗?
∴∠ADB=∠ADC=90 °
△ABD和△ACD是直角三角形
(2)要注意是哪三线.
等腰三角形的底边上的高、中线及顶角的平分线
互相重合,简称“三线合一”
(1)“等腰三角形”是三线合一的大前提.
C
A
B
D
问题2、结论(3)、(4)、(5)用一句话可以归纳为什么?
思考2:你有办法证明等腰三角形的“三线合一”吗?
小结:等腰三角形的性质
1、等腰三角形的两个底角相等
(简称“等边对等角”)
2、等腰三角形的
底边上的高、底边上的中线和顶角的平分线
互相重合(简称“三线合一”)
一般的三角形有这种性质吗?
要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。
C
D
B
A
①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )
几何语言:
等边对等角
(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___
(2)∵AD是中线,∴___⊥___ ,∠____ =∠____
(3)∵AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
②在△ABC中, AB=AC时,
等腰三角形底边上的中线和高线、顶角的平分线互相重合。
例1、已知:在△ABC中,AB = AC,∠B = 80°,
求∠C 和 ∠A的度数。
A
B
C
解:
∵ AB =AC
∴ ∠B = ∠C = 80°
又 ∵ ∠A + ∠ B + ∠C = 180°
∴ ∠A = 180°- 80° - 80°= 20°
例2、如图,在△ABC中,AB = AC,D是BC边上的中点,∠B = 30°,求 ∠1 和 ∠ADC的度数。
A
B
C
1
2
D
解:
∵ AB = AC
∴ ∠B = ∠C =30°
∵ D是BC边上的中点
∴AD⊥BC, ∠1= ∠2
∴ ∠ADC = ∠ADB= 90°
∵ ∠ 1 =180° - ∠ADB - ∠B = 60°
∴ ∠ 1= 60°
等边三角形
一.基本概念
1.定义:
三条边都相等的三角形叫做等边三角形. (正三角形)
如图AB=AC=BC ,△ABC就是等边三角形
2.等边三角形的基本性质:
三条边都相等.即AB=AC=BC
三个角都相等.即:
∠A=∠B=∠C=60°
A
B
C
1.等腰三角形一个角为70°,它的另外两个角为
___________________
2.等腰三角形一个角为110°,它的另外两个角为________
70°,40°或55°,55°
35°,35°
3.等腰三角形有两边长为4和8,则该等腰三角形的周长为__________
20
4.练习、判断下列命题是否正确。
(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°。 ( )
(3)等腰三角形的底角都是锐角。 ( )
(4)钝角三角形不可能是等腰三角形。 ( )
×
×
√
√
1、等腰三角形的性质:
等边对等角
2、等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合(三线合一)
3、“三线合一”性质在实际应用中,只要推出
其中一个 结论成立,其它两个结论一定成立,
所以关键是寻找其中一个结论成立的条件。
4、等边三角形的性质。
1.P81 练习题
2.P84 习题13.3 1、2、4.
布置作业
谢 谢
等腰三角形的性质
Contents
目录
01
02
03
04
牛刀小试
例题演示
新知探究
新课导入
05
深入探究
课堂小结
06
等腰三角形
一.基本概念
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC , 就是等腰三角形
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
C
A
B
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
做一做1:
在半透明的纸上,画一个等腰三角形,把它对折,让两腰AB,AC重叠在一起,折痕为AD。
观察后你发现了什么现象?
二.等腰三角形性质的探索
B
A
C
D
A
B
C
D
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD ,AD为顶角平分线
问题1、结论(2)用文字如何表述?
等腰三角形的两个底角相等(简写“等边对等角”)
C
A
B
D
结论:
C
A
B
D
如何证明:等腰三角形的两个底角相等?
已知:如图△ABC中,AB=AC.
求证:∠B=∠C.
证明:过A作AD⊥BC于D
∟
在Rt△ABD和Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt△ABD≌Rt△ACD(H.L.)
∴∠B=∠C(全等三角形的对应角相等)
思考1:还有其他的证明方法吗?
∴∠ADB=∠ADC=90 °
△ABD和△ACD是直角三角形
(2)要注意是哪三线.
等腰三角形的底边上的高、中线及顶角的平分线
互相重合,简称“三线合一”
(1)“等腰三角形”是三线合一的大前提.
C
A
B
D
问题2、结论(3)、(4)、(5)用一句话可以归纳为什么?
思考2:你有办法证明等腰三角形的“三线合一”吗?
小结:等腰三角形的性质
1、等腰三角形的两个底角相等
(简称“等边对等角”)
2、等腰三角形的
底边上的高、底边上的中线和顶角的平分线
互相重合(简称“三线合一”)
一般的三角形有这种性质吗?
要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。
C
D
B
A
①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )
几何语言:
等边对等角
(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___
(2)∵AD是中线,∴___⊥___ ,∠____ =∠____
(3)∵AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
②在△ABC中, AB=AC时,
等腰三角形底边上的中线和高线、顶角的平分线互相重合。
例1、已知:在△ABC中,AB = AC,∠B = 80°,
求∠C 和 ∠A的度数。
A
B
C
解:
∵ AB =AC
∴ ∠B = ∠C = 80°
又 ∵ ∠A + ∠ B + ∠C = 180°
∴ ∠A = 180°- 80° - 80°= 20°
例2、如图,在△ABC中,AB = AC,D是BC边上的中点,∠B = 30°,求 ∠1 和 ∠ADC的度数。
A
B
C
1
2
D
解:
∵ AB = AC
∴ ∠B = ∠C =30°
∵ D是BC边上的中点
∴AD⊥BC, ∠1= ∠2
∴ ∠ADC = ∠ADB= 90°
∵ ∠ 1 =180° - ∠ADB - ∠B = 60°
∴ ∠ 1= 60°
等边三角形
一.基本概念
1.定义:
三条边都相等的三角形叫做等边三角形. (正三角形)
如图AB=AC=BC ,△ABC就是等边三角形
2.等边三角形的基本性质:
三条边都相等.即AB=AC=BC
三个角都相等.即:
∠A=∠B=∠C=60°
A
B
C
1.等腰三角形一个角为70°,它的另外两个角为
___________________
2.等腰三角形一个角为110°,它的另外两个角为________
70°,40°或55°,55°
35°,35°
3.等腰三角形有两边长为4和8,则该等腰三角形的周长为__________
20
4.练习、判断下列命题是否正确。
(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°。 ( )
(3)等腰三角形的底角都是锐角。 ( )
(4)钝角三角形不可能是等腰三角形。 ( )
×
×
√
√
1、等腰三角形的性质:
等边对等角
2、等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合(三线合一)
3、“三线合一”性质在实际应用中,只要推出
其中一个 结论成立,其它两个结论一定成立,
所以关键是寻找其中一个结论成立的条件。
4、等边三角形的性质。
1.P81 练习题
2.P84 习题13.3 1、2、4.
布置作业
谢 谢
