华东师大版数学八年级上册 13.5.3角平分线 课件(共16张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.5.3角平分线 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 985.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 17:13:29 | ||
图片预览




文档简介
(共16张PPT)
角平分线
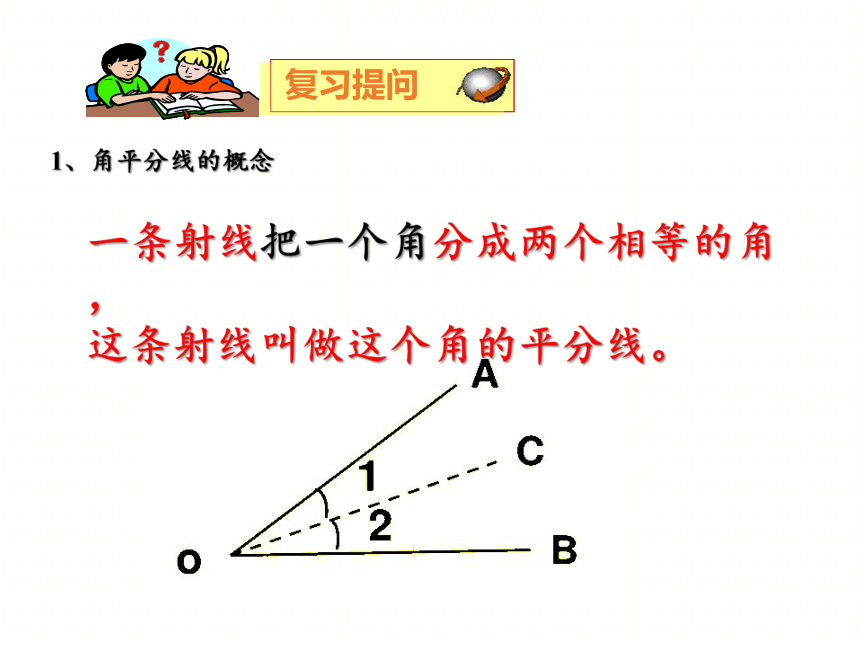
1、角平分线的概念
一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线。
随堂练习
随堂练习
复习提问
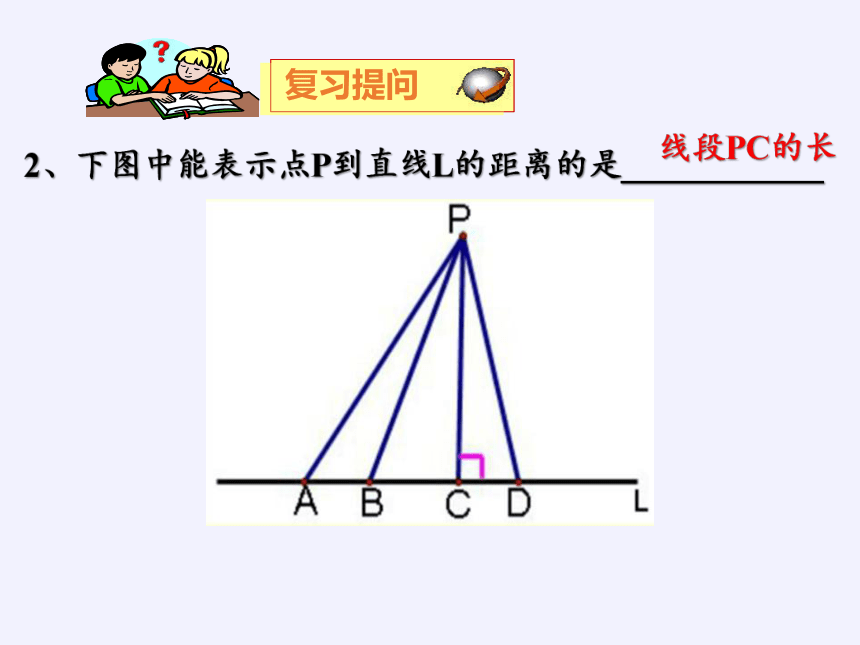
2、下图中能表示点P到直线L的距离的是____________
线段PC的长
随堂练习
随堂练习
复习提问
3、下列两图中,能表示直线L1上一点P
到直线L2的距离的是( )
图1
4、下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
图1
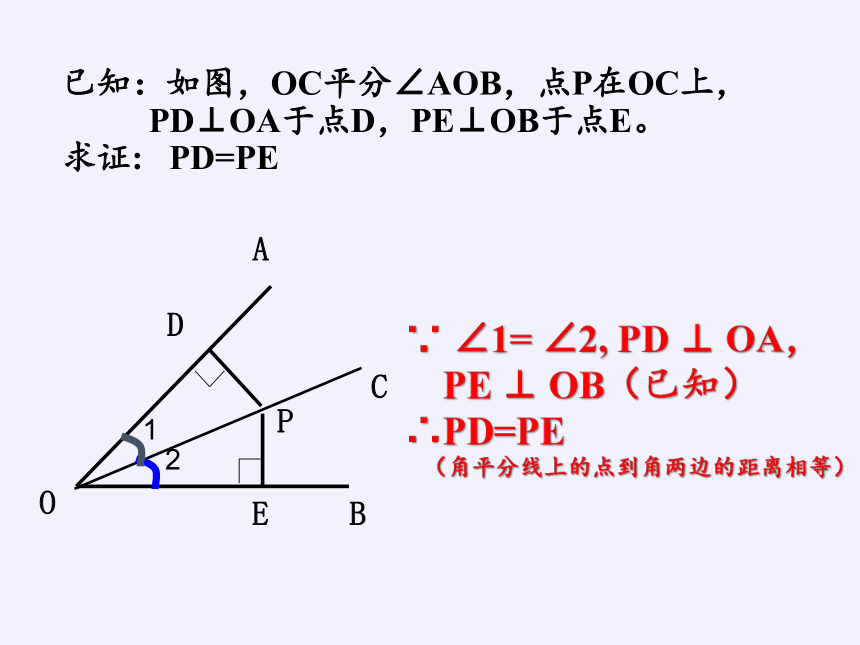
已知:如图,OC平分∠AOB,点P在OC上,
PD⊥OA于点D,PE⊥OB于点E。
求证: PD=PE
P
A
O
B
C
E
D
1
2
∵ ∠1= ∠2, PD ⊥ OA,
PE ⊥ OB(已知)∴PD=PE
(角平分线上的点到角两边的距离相等)
已知:如图, PD=PE ,点P在OC上,
PD⊥OA于点D,PE⊥OB于点E。
求证: OC平分∠AOB
P
A
O
B
C
E
D
1
2
∵ PD=PE, PD ⊥ OA,
PE ⊥ OB(已知)
∴ OC平分∠AOB
(角的内部到角两边距离相等的点在角的平分线上)
1、判断题( )
∵ 如图,AD平分∠BAC(已知)
∴BD = DC
( )
角的平分线上的点到角的两边的距离相等。
×
2、判断题( )
∵如图,DC⊥AC, DB⊥AB (已知)
∴BD = DC
(角平分线上的点到角的两边的距离相等 )
×
2、填空题
∵∠1= ∠2,DC⊥AC, DE⊥AB
∴_________
(________________________________)
A
C
D
E
B
1
2
DC=DE
角平分线上的点到角的两边的距离相等
做完本题后, 你能说出△ADE的周长是哪两条线段的和吗?
思考
思考分析
命题:三角形三个角的平分线相交于一点.
如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D.
∵BM是△ABC的角平分线,点P在BM上,
∴△ABC的三条角平分线相交于一点P.
基本想法是这样的:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考虑前面刚刚学习的内容.
A
B
C
P
M
N
D
E
F
∴PD=PE(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PF.
∴点P在∠BAC的平分线上(角的内部到角两边距离相等的点在角的平分线上).
小结拓展
小结拓展
谢 谢
角平分线
1、角平分线的概念
一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线。
随堂练习
随堂练习
复习提问
2、下图中能表示点P到直线L的距离的是____________
线段PC的长
随堂练习
随堂练习
复习提问
3、下列两图中,能表示直线L1上一点P
到直线L2的距离的是( )
图1
4、下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
图1
已知:如图,OC平分∠AOB,点P在OC上,
PD⊥OA于点D,PE⊥OB于点E。
求证: PD=PE
P
A
O
B
C
E
D
1
2
∵ ∠1= ∠2, PD ⊥ OA,
PE ⊥ OB(已知)∴PD=PE
(角平分线上的点到角两边的距离相等)
已知:如图, PD=PE ,点P在OC上,
PD⊥OA于点D,PE⊥OB于点E。
求证: OC平分∠AOB
P
A
O
B
C
E
D
1
2
∵ PD=PE, PD ⊥ OA,
PE ⊥ OB(已知)
∴ OC平分∠AOB
(角的内部到角两边距离相等的点在角的平分线上)
1、判断题( )
∵ 如图,AD平分∠BAC(已知)
∴BD = DC
( )
角的平分线上的点到角的两边的距离相等。
×
2、判断题( )
∵如图,DC⊥AC, DB⊥AB (已知)
∴BD = DC
(角平分线上的点到角的两边的距离相等 )
×
2、填空题
∵∠1= ∠2,DC⊥AC, DE⊥AB
∴_________
(________________________________)
A
C
D
E
B
1
2
DC=DE
角平分线上的点到角的两边的距离相等
做完本题后, 你能说出△ADE的周长是哪两条线段的和吗?
思考
思考分析
命题:三角形三个角的平分线相交于一点.
如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D.
∵BM是△ABC的角平分线,点P在BM上,
∴△ABC的三条角平分线相交于一点P.
基本想法是这样的:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考虑前面刚刚学习的内容.
A
B
C
P
M
N
D
E
F
∴PD=PE(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PF.
∴点P在∠BAC的平分线上(角的内部到角两边距离相等的点在角的平分线上).
小结拓展
小结拓展
谢 谢
