华东师大版数学八年级上册 14.1.2 直角三角形的判定 课件(共20张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 14.1.2 直角三角形的判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1009.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 17:14:49 | ||
图片预览






文档简介
(共20张PPT)
14.1.2 直角三角形的判定
华师大版八年级上册
复习旧知,孕育新课
a2 +b 2=c2
???
问题一:如图,在△ABC中,∠C=90°,
⑴已知a=6,b=8,则c=
⑵已知b=12,c=13, 则a=
10
5
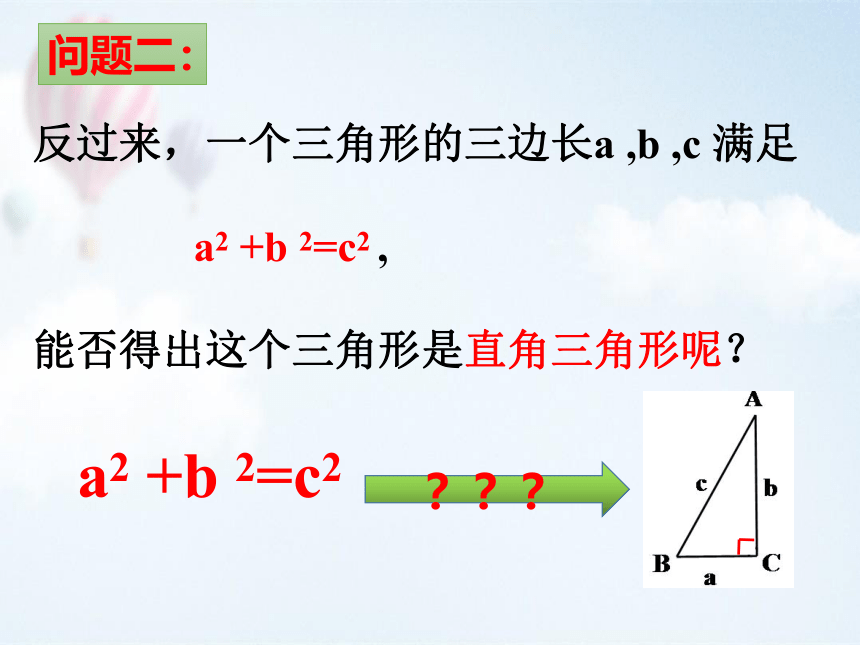
问题二:
反过来,一个三角形的三边长a ,b ,c 满足
a2 +b 2=c2 ,
能否得出这个三角形是直角三角形呢?
a2 +b 2=c2
???
张雪芬
14.1.2 直角三角形的判定
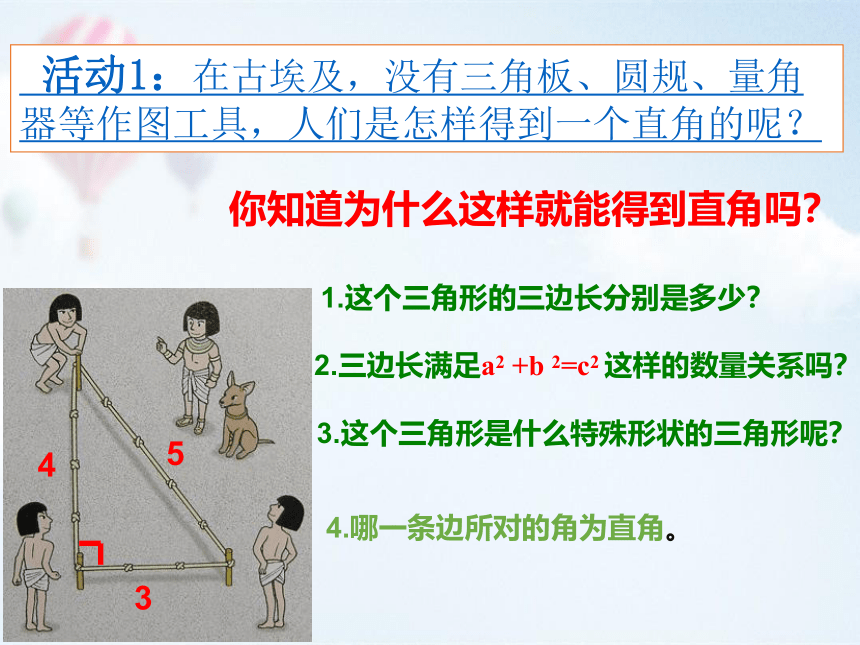
2.三边长满足a2 +b 2=c2 这样的数量关系吗?
你知道为什么这样就能得到直角吗?
4
3
5
活动1:在古埃及,没有三角板、圆规、量角器等作图工具,人们是怎样得到一个直角的呢?
1.这个三角形的三边长分别是多少?
3.这个三角形是什么特殊形状的三角形呢?
4.哪一条边所对的角为直角。
2.用你的量角器测量一下这个三角形的最大角的度数。
3.请判断一下这个三角形的形状.
活动2:把你手中6cm、8cm、10cm的小塑料棒
拼成一个三角形.
1.三边长是否也满足 a2 +b 2=c2 数量关系?
4.哪一条边所对的角为直角。
动手操作,探索规律:
2.用你的量角器测量一下这个三角形的最大角的度数。
3.请判断一下这个三角形的形状.
1.三边长是否也满足 a2 +b 2=c2 数量关系?
4.哪一条边所对的角为直角。
活动3:用圆规、直尺画一个△ABC, 使它的三
边长分别为: 5cm、12cm、13cm
三、得出猜想:
如果一个三角形的三边长a ,b ,c 满足
a2 +b 2=c2 ,
那么这个三角形是直角三角形,
且边c所对的角为直角。
如何验证这个猜想是正确的呢?
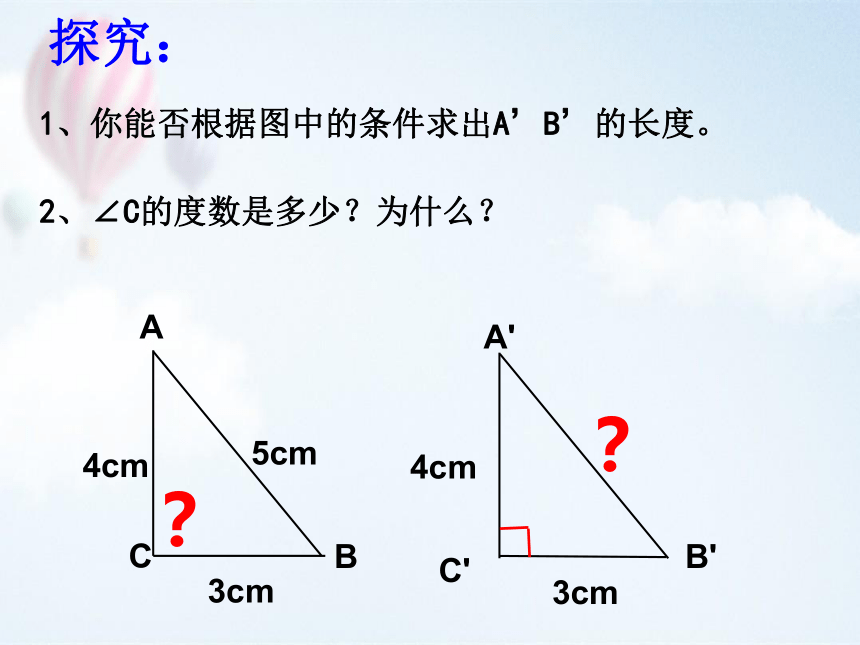
探究:
3cm
4cm
5cm
3cm
4cm
C
A
B
A'
B'
C'
1、你能否根据图中的条件求出A’B’的长度。
2、∠C的度数是多少?为什么?
?
?
如果一个三角形的三边长a、b、c满足a2+b2=c2,
那么这个三角形是直角三角形。
直角三角形
已知:如图,在△ABC中,
求证:△ABC是直角三角形
BC=a,
AC=b,
AB=c,
a2+b2=c2
a2+b2=c2
四:小组合作,论证猜想
已知:如图,在△ABC中,AB=c,BC=a,
AC=b,a2+b2=c2
求证:△ABC是直角三角形
证明:作△A'B'C',使
∠C'=900,B'C'=a,A'C'=b,
在△ABC和△A'B'C'中
BC=a=B'C'
AC=b=A'C'
AB=c=A'B'
∴∠C=∠C'=900
∴△ABC≌△A'B'C'(S.S.S.)
B'
C'
a
A'
b
C
则A'B'=√a2+b2
=c
=√c2
∴△ABC是直角三角形
勾股定理的逆定理:如果三角形的三边长a、b、c有关系 ,那么这个三角形是直角三角形,且边c所对的角是直角。
a2 + b2 = c2
符号语言:
得出结论:
例1:判断由线段a,b,c组成的三角形是不是直角三角形
(1) a=7,b=24,c=25; (2) a=8,b=17,c=15
解:(1)最长边为25
∵a2+b2=72+242
=49+576 =625
c2=252 =625
∴a2+b2=c2
∴以8,15,17为边长的三角形是直角三角形.
解:(2)最长边为17
∵a2+c2=82+152
=64+225 =289
b2=172 =289
∴a2+c2=b2
∴以7, 24, 25为边长的三角形是直角三角形.
典例剖析
你知道吗?
运用勾股定理逆定理的步骤有哪些?
(1)首先找出最长边。
(2)计算:两条较短边的平方和是否等于最长边的平方。
(3)判定:若相等,则△ABC是直角三角形.
像这些能够成为直角三角形三条边长的三个正整数,称为勾股数.
3、4、5
5、12、13
7、24、25
8、15、17
勾股数
思考:像1.5、2、2.5这组数据能不能构成直角三角形?
是不是勾股数?
6、8、10
当堂检测
1、以下各组数为边长,能组成直角三角形的( ).
A.4,6,8 B.10,8,9
C.7,25,24 D.9,17,15
2.若一个三角形的三条边长a,b,c满足
则这个三角形是 三角形。
3、如图,一块四边形的地,测得四边长如图所示,且∠ABC=900,求这个四边形地的面积。
(单位:米)
C
直角
3.如图,一块四边形的地,测得四边长如图所示,且∠ABC=900,求这个四边形地的面积。
(单位:米)
5
解:
连结AC
在RT△ABC中
AC=√AB2+BC2
=√32+42
=5
在△ACD中
AC2+AD2
=52+122=169
CD2=132=169
∴AC2+AD2=CD2
∴△ACD是直角三角形且∠CAD=900
∴S四边形ABCD=S△ABC+S△ACD
课堂小结
今天你新学习了什么定理?
它的意义是什么?作用是什么?
你是如何学习它的?
在证明结论时用了什么方法?你的思路是什么?
你在学习过程中有哪些新的体验和收获?
感受到了哪些思想方法?
练 习
P 114
第1、2、3题
谢谢
14.1.2 直角三角形的判定
华师大版八年级上册
复习旧知,孕育新课
a2 +b 2=c2
???
问题一:如图,在△ABC中,∠C=90°,
⑴已知a=6,b=8,则c=
⑵已知b=12,c=13, 则a=
10
5
问题二:
反过来,一个三角形的三边长a ,b ,c 满足
a2 +b 2=c2 ,
能否得出这个三角形是直角三角形呢?
a2 +b 2=c2
???
张雪芬
14.1.2 直角三角形的判定
2.三边长满足a2 +b 2=c2 这样的数量关系吗?
你知道为什么这样就能得到直角吗?
4
3
5
活动1:在古埃及,没有三角板、圆规、量角器等作图工具,人们是怎样得到一个直角的呢?
1.这个三角形的三边长分别是多少?
3.这个三角形是什么特殊形状的三角形呢?
4.哪一条边所对的角为直角。
2.用你的量角器测量一下这个三角形的最大角的度数。
3.请判断一下这个三角形的形状.
活动2:把你手中6cm、8cm、10cm的小塑料棒
拼成一个三角形.
1.三边长是否也满足 a2 +b 2=c2 数量关系?
4.哪一条边所对的角为直角。
动手操作,探索规律:
2.用你的量角器测量一下这个三角形的最大角的度数。
3.请判断一下这个三角形的形状.
1.三边长是否也满足 a2 +b 2=c2 数量关系?
4.哪一条边所对的角为直角。
活动3:用圆规、直尺画一个△ABC, 使它的三
边长分别为: 5cm、12cm、13cm
三、得出猜想:
如果一个三角形的三边长a ,b ,c 满足
a2 +b 2=c2 ,
那么这个三角形是直角三角形,
且边c所对的角为直角。
如何验证这个猜想是正确的呢?
探究:
3cm
4cm
5cm
3cm
4cm
C
A
B
A'
B'
C'
1、你能否根据图中的条件求出A’B’的长度。
2、∠C的度数是多少?为什么?
?
?
如果一个三角形的三边长a、b、c满足a2+b2=c2,
那么这个三角形是直角三角形。
直角三角形
已知:如图,在△ABC中,
求证:△ABC是直角三角形
BC=a,
AC=b,
AB=c,
a2+b2=c2
a2+b2=c2
四:小组合作,论证猜想
已知:如图,在△ABC中,AB=c,BC=a,
AC=b,a2+b2=c2
求证:△ABC是直角三角形
证明:作△A'B'C',使
∠C'=900,B'C'=a,A'C'=b,
在△ABC和△A'B'C'中
BC=a=B'C'
AC=b=A'C'
AB=c=A'B'
∴∠C=∠C'=900
∴△ABC≌△A'B'C'(S.S.S.)
B'
C'
a
A'
b
C
则A'B'=√a2+b2
=c
=√c2
∴△ABC是直角三角形
勾股定理的逆定理:如果三角形的三边长a、b、c有关系 ,那么这个三角形是直角三角形,且边c所对的角是直角。
a2 + b2 = c2
符号语言:
得出结论:
例1:判断由线段a,b,c组成的三角形是不是直角三角形
(1) a=7,b=24,c=25; (2) a=8,b=17,c=15
解:(1)最长边为25
∵a2+b2=72+242
=49+576 =625
c2=252 =625
∴a2+b2=c2
∴以8,15,17为边长的三角形是直角三角形.
解:(2)最长边为17
∵a2+c2=82+152
=64+225 =289
b2=172 =289
∴a2+c2=b2
∴以7, 24, 25为边长的三角形是直角三角形.
典例剖析
你知道吗?
运用勾股定理逆定理的步骤有哪些?
(1)首先找出最长边。
(2)计算:两条较短边的平方和是否等于最长边的平方。
(3)判定:若相等,则△ABC是直角三角形.
像这些能够成为直角三角形三条边长的三个正整数,称为勾股数.
3、4、5
5、12、13
7、24、25
8、15、17
勾股数
思考:像1.5、2、2.5这组数据能不能构成直角三角形?
是不是勾股数?
6、8、10
当堂检测
1、以下各组数为边长,能组成直角三角形的( ).
A.4,6,8 B.10,8,9
C.7,25,24 D.9,17,15
2.若一个三角形的三条边长a,b,c满足
则这个三角形是 三角形。
3、如图,一块四边形的地,测得四边长如图所示,且∠ABC=900,求这个四边形地的面积。
(单位:米)
C
直角
3.如图,一块四边形的地,测得四边长如图所示,且∠ABC=900,求这个四边形地的面积。
(单位:米)
5
解:
连结AC
在RT△ABC中
AC=√AB2+BC2
=√32+42
=5
在△ACD中
AC2+AD2
=52+122=169
CD2=132=169
∴AC2+AD2=CD2
∴△ACD是直角三角形且∠CAD=900
∴S四边形ABCD=S△ABC+S△ACD
课堂小结
今天你新学习了什么定理?
它的意义是什么?作用是什么?
你是如何学习它的?
在证明结论时用了什么方法?你的思路是什么?
你在学习过程中有哪些新的体验和收获?
感受到了哪些思想方法?
练 习
P 114
第1、2、3题
谢谢
