华东师大版数学八年级上册 第12章 整式的乘除 复习 课件(共25张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 第12章 整式的乘除 复习 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 580.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第12章 整式的乘除 复习课件
重难点知识归纳
重点:整式的乘除法,乘法公式的应用。
难点:整式乘法公式的应用。
要突破上述难点,先要认真掌握好乘法公式的基本结构,再要针对性地加强练习,以达到熟练自如的目的。
知识表解
研究性学习
学习本章知识,先得有较好的转化意识,即善于化新为旧,如把单项式乘法转化为有理数乘法和同底数幂的乘法等,这样,新知识的学习就不难了。
同时要特别逆用一些法则、公式,这样会为解题提供方便、简洁的解法,也锻炼了思维能力。
解题方法技巧
1.归纳法:如本章的一些性质、法则、公式的导出,一般都是由特殊到一般归纳得到的。
2.转化法: 如单项式乘法转化为有理数乘法和同底数幂的乘法等。
3.整体代换法: 如公式中的字母a、b不仅表示数,也可以表示单项式、多项式。
4.反向思考法:如逆用乘法公式解题等。
中考考向分析
热点:整式的乘除法、整式乘法的应用。
冷点:整式乘除法中技巧性解题方法。
本章知识在中考中主要以选择、填空题予以考查,少数中档题考查乘法公式的应用,约占中考试卷的7%左右。
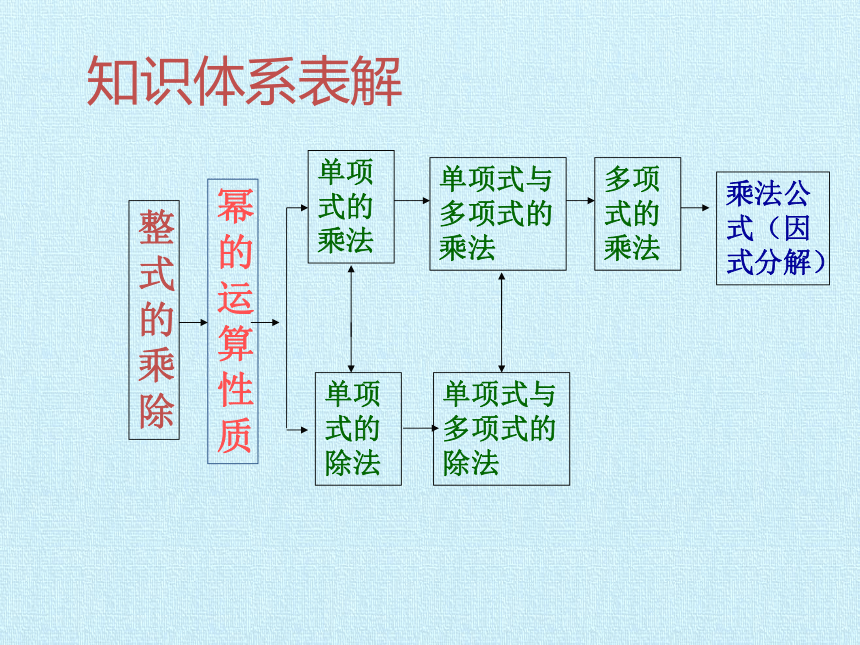
幂的运算性质
整式的乘除
单项式与多项式的乘法
单项式的乘法
多项式的乘法
乘法公式(因式分解)
单项式的除法
单项式与多项式的除法
知识体系表解
同底数幂的乘法
am an=am+n (m、n都是正整数)
(am)n=amn (m、n都是正整数)
幂的乘方
积的乘方
(ab)=an bn (n是正整数)
同底数幂的除法
1.am ÷an=am-n
(a≠0,m、n都是正整数,m>n)
2.a0=1,(a≠0 )
3.
单项式乘法
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一
个单项式里出现的字母,则连同
它的指数作为积的一个因式。
多项式乘以单项式
多项式乘以单项式,用单项式去乘以多项式的每一项,并把所得的积相加。
多项式乘以多项式
多项式乘以多项式,用一个多项式的每一项去乘以另一个多项式的每一项,并把所得的积相加。
乘法公式(因式分解)
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a-b)=a2-b2
(a±b) =a2± 2ab+b2
单项式的除法
单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。
多项式除以单项式
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
检测练习
一、选择题
1.下列运算正确的是( )
A.(x-2)2=x2-4 B.x3·x4=x12
C.x6÷x3=x2 D.(x2)3=x6
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(2y-x)(-x-2y)
C.(x-2y)(-x-2y) D.(-2y-x)(x+2y)
D
D
B
A
5.多项式4x2+1加上一个单项式后,使它能成为一个整式的平方,则加上的单项式不可以是( )
A.4x B.-4x C.4x4 D.-4x4
6.已知a2+a-3=0,那么a2(a+4)的值是( )
A.9 B.-12 C.-18 D.-15
D
A
7.如图,以点O为圆心的20个同心圆,它们的半径从小到大依次是1,2,3,4,……,20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,……,第19个圆和第20个圆形成的所有圆环,则阴影部分的面积为( )
A.231π B.210π C.190π D.171π
B
二、填空题
8.多项式x2+mx+5因式分解得(x+5)(x+n),则m=____,n=____。
9.若6x=3,6y=2,则62x-3y=____。
10.(2016·福州)若x+y=10,xy=1,则x3y+xy3的值是____。
11.已知(x+p)(x+q)的展开式中不含x的一次项,则p,q之间的关系是_____________。
12.观察下列等式:4×1×2+1=32;4×2×3+1=52;4×3×4+1=72;4×4×5+1=92;用含正整数n的等式表示上述规律________________________________________。
6
1
98
p+q=0
4n(n+1)+1=(2n+1)2
三、解答题
13.计算:
(1)(-2xy2)2·3x2y÷(-6x3y4);
解:-2xy
(2)(8an+2+4an+1-2an)÷2an-1;
解:4a3+2a2-a
(3)(x-y)2-(x-2y)(x+y);
解:3y2-xy
(4)(-2a-3b)2-(b-2a)(-2a-b)。
解:12ab+10b2
14.分解因式:
(1)p3(a-1)+p(1-a);
解:p(a-1)(p+1)(p-1)
(3)(2m+n)(2m+n-6)+9;
解:(2m+n-3)2
(4)16x2y2-(x2+4y2)2。
解:-(x+2y)2(x-2y)2
16.(1)填空:
(a-b)(a+b)=_________;
(a-b)(a2+ab+b2)=_________;
(a-b)(a3+a2b+ab2+b3)=__________。
(2)猜想:(a-b)(an-1+an-2b+……+abn-2+bn-1)=_______(其中n为正整数,且n≥2)。
(3)利用(2)猜想的结论计算:
29-28+27-……+23-22+2。
解:在(a-b)(an-1+an-2b+…+abn-2+bn-1)=an-bn中,取a=2,b=-1,n=10,得(2+1)(29-28+27-…+23-22+2-1)=210-(-1)10,即3(29-28+27-…+23-22+2-1)=1023,29-28+27-…+23-22+2-1=341,∴29-28+27-…+23-22+2=342。
a2-b2
a3-b3
a4-b4
an-bn
。
谢 谢
第12章 整式的乘除 复习课件
重难点知识归纳
重点:整式的乘除法,乘法公式的应用。
难点:整式乘法公式的应用。
要突破上述难点,先要认真掌握好乘法公式的基本结构,再要针对性地加强练习,以达到熟练自如的目的。
知识表解
研究性学习
学习本章知识,先得有较好的转化意识,即善于化新为旧,如把单项式乘法转化为有理数乘法和同底数幂的乘法等,这样,新知识的学习就不难了。
同时要特别逆用一些法则、公式,这样会为解题提供方便、简洁的解法,也锻炼了思维能力。
解题方法技巧
1.归纳法:如本章的一些性质、法则、公式的导出,一般都是由特殊到一般归纳得到的。
2.转化法: 如单项式乘法转化为有理数乘法和同底数幂的乘法等。
3.整体代换法: 如公式中的字母a、b不仅表示数,也可以表示单项式、多项式。
4.反向思考法:如逆用乘法公式解题等。
中考考向分析
热点:整式的乘除法、整式乘法的应用。
冷点:整式乘除法中技巧性解题方法。
本章知识在中考中主要以选择、填空题予以考查,少数中档题考查乘法公式的应用,约占中考试卷的7%左右。
幂的运算性质
整式的乘除
单项式与多项式的乘法
单项式的乘法
多项式的乘法
乘法公式(因式分解)
单项式的除法
单项式与多项式的除法
知识体系表解
同底数幂的乘法
am an=am+n (m、n都是正整数)
(am)n=amn (m、n都是正整数)
幂的乘方
积的乘方
(ab)=an bn (n是正整数)
同底数幂的除法
1.am ÷an=am-n
(a≠0,m、n都是正整数,m>n)
2.a0=1,(a≠0 )
3.
单项式乘法
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一
个单项式里出现的字母,则连同
它的指数作为积的一个因式。
多项式乘以单项式
多项式乘以单项式,用单项式去乘以多项式的每一项,并把所得的积相加。
多项式乘以多项式
多项式乘以多项式,用一个多项式的每一项去乘以另一个多项式的每一项,并把所得的积相加。
乘法公式(因式分解)
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a-b)=a2-b2
(a±b) =a2± 2ab+b2
单项式的除法
单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。
多项式除以单项式
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
检测练习
一、选择题
1.下列运算正确的是( )
A.(x-2)2=x2-4 B.x3·x4=x12
C.x6÷x3=x2 D.(x2)3=x6
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(2y-x)(-x-2y)
C.(x-2y)(-x-2y) D.(-2y-x)(x+2y)
D
D
B
A
5.多项式4x2+1加上一个单项式后,使它能成为一个整式的平方,则加上的单项式不可以是( )
A.4x B.-4x C.4x4 D.-4x4
6.已知a2+a-3=0,那么a2(a+4)的值是( )
A.9 B.-12 C.-18 D.-15
D
A
7.如图,以点O为圆心的20个同心圆,它们的半径从小到大依次是1,2,3,4,……,20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,……,第19个圆和第20个圆形成的所有圆环,则阴影部分的面积为( )
A.231π B.210π C.190π D.171π
B
二、填空题
8.多项式x2+mx+5因式分解得(x+5)(x+n),则m=____,n=____。
9.若6x=3,6y=2,则62x-3y=____。
10.(2016·福州)若x+y=10,xy=1,则x3y+xy3的值是____。
11.已知(x+p)(x+q)的展开式中不含x的一次项,则p,q之间的关系是_____________。
12.观察下列等式:4×1×2+1=32;4×2×3+1=52;4×3×4+1=72;4×4×5+1=92;用含正整数n的等式表示上述规律________________________________________。
6
1
98
p+q=0
4n(n+1)+1=(2n+1)2
三、解答题
13.计算:
(1)(-2xy2)2·3x2y÷(-6x3y4);
解:-2xy
(2)(8an+2+4an+1-2an)÷2an-1;
解:4a3+2a2-a
(3)(x-y)2-(x-2y)(x+y);
解:3y2-xy
(4)(-2a-3b)2-(b-2a)(-2a-b)。
解:12ab+10b2
14.分解因式:
(1)p3(a-1)+p(1-a);
解:p(a-1)(p+1)(p-1)
(3)(2m+n)(2m+n-6)+9;
解:(2m+n-3)2
(4)16x2y2-(x2+4y2)2。
解:-(x+2y)2(x-2y)2
16.(1)填空:
(a-b)(a+b)=_________;
(a-b)(a2+ab+b2)=_________;
(a-b)(a3+a2b+ab2+b3)=__________。
(2)猜想:(a-b)(an-1+an-2b+……+abn-2+bn-1)=_______(其中n为正整数,且n≥2)。
(3)利用(2)猜想的结论计算:
29-28+27-……+23-22+2。
解:在(a-b)(an-1+an-2b+…+abn-2+bn-1)=an-bn中,取a=2,b=-1,n=10,得(2+1)(29-28+27-…+23-22+2-1)=210-(-1)10,即3(29-28+27-…+23-22+2-1)=1023,29-28+27-…+23-22+2-1=341,∴29-28+27-…+23-22+2=342。
a2-b2
a3-b3
a4-b4
an-bn
。
谢 谢
