北师大版九年级数学下册3.6直线与圆的位置关系课件(共29张PPT)
文档属性
| 名称 | 北师大版九年级数学下册3.6直线与圆的位置关系课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 07:53:58 | ||
图片预览





文档简介
(共29张PPT)
直线与圆的位置关系
考点梳理
直线和圆的位置关系
1
切线的性质
2
切线的判定
3
切线长定理
4
内心、外心
5
1
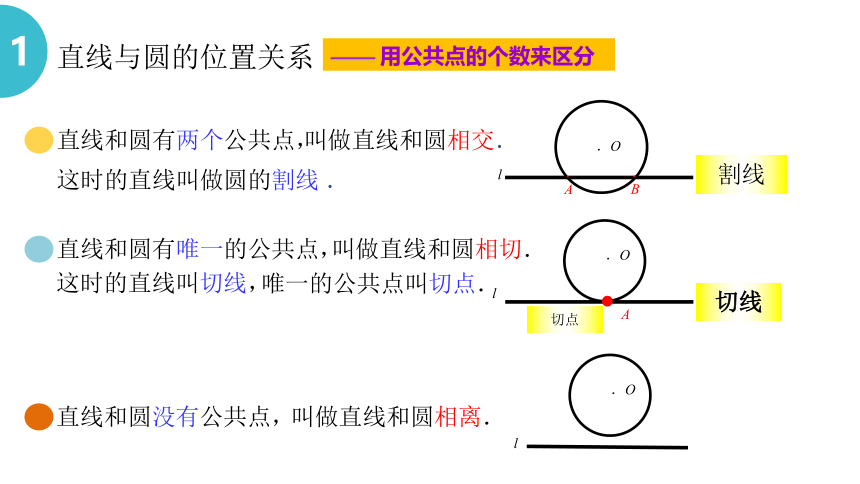
直线与圆的位置关系
—— 用公共点的个数来区分
1
.O
l
.O
叫做直线和圆相离.
直线和圆没有公共点,
l
直线和圆有唯一的公共点,
叫做直线和圆相切.
唯一的公共点叫切点.
.O
l
直线和圆有两个公共点,
叫做直线和圆相交.
这时的直线叫做圆的割线 .
.A
.B
切点
割线
切线
这时的直线叫切线,
A
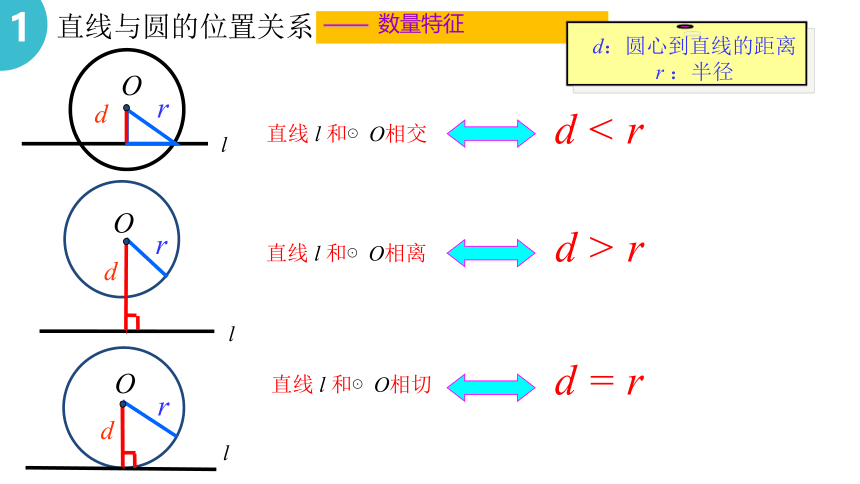
直线与圆的位置关系
—— 数量特征
1
r
d
直线 l 和⊙O相交
O
d
r
直线 l 和⊙O相切
O
l
d < r
d = r
d:圆心到直线的距离
r :半径
d
r
直线 l 和⊙O相离
O
l
d > r
l
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_______________________的关系来判断.
(在实际应用中,常采用第二种方法判定)
两
直线与圆的公共点
圆心到直线的距离与半径
小结
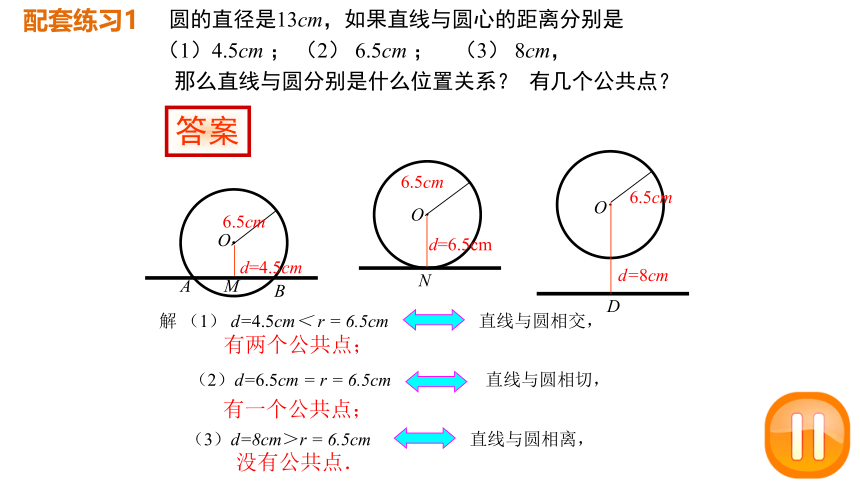
答案
(3)d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
配套练习1
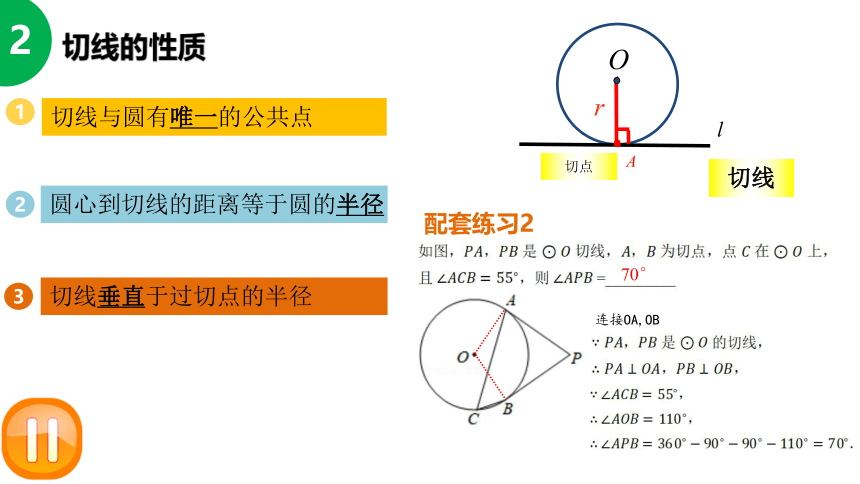
2
切线与圆有唯一的公共点
2
圆心到切线的距离等于圆的半径
切线垂直于过切点的半径
r
O
l
切线
切点
A
配套练习2
70°
1
2
3
连接OA,OB
3
3
圆心到直线的距离等于圆的半径,则此直线是圆的切线.
r
O
l
切线
切点
A
1
2
经过圆上一点,且与过这一点的半径①垂直②的直线是圆的切线。
题型一:连半径, 证垂直
题型二:作垂直, 证半径
3
题型一:连半径, 证垂直
证明某直线是圆的切线时, 如果已知直线与圆有公共点, 那么可作出经过该点的半径, 证明直线垂直于该半径,则可证明是切线, 即“有交点, 连半径, 证垂直”.
3
配套练习3
切线的证明:连半径, 证垂直
如图以△ABC的BC边上一 点O为圆心的圆经过A, B两点, 且与BC边交于点E,
D为BE下方的半圆的中点, 连接AD交BC于点F, 且 AC=FC. 求证:AC是⊙O的切线.
证明:如图, 连接OA, OD.
∵OA=OD, ∴∠OAD=∠ODA.
∵D为BE下方的半圆的中点, ∴OD⊥BE,
∴∠ODA+∠OFD=90° .
∵AC=FC, ∴∠FAC=∠AFC.
又∵∠OFD=∠AFC, ∴∠OFD=∠FAC, ∴∠OAD+∠FAC=∠ODA+∠OFD=90°, 即∠OAC=90° .
又∵OA是⊙O的半径, ∴AC是⊙O的切线.
3
题型二:作垂直, 证半径
证明某直线是圆的切线时, 如果已知直线与圆有公共点, 那么可作出经过该点的半径, 证明直线垂直于该半径, 则可证明是切线,即“有交点, 连半径, 证垂直”.
3
配套练习4
切线的证明:作垂直, 证半径
如图,△ABC为等腰三角形, AB=AC, O是底边BC的中点,
⊙O与腰AB相切于点D. 求证:AC与⊙O相切.
分析 AC与⊙O的交点不明确,所以可过圆心O作OE⊥AC于点E, 证明OE的长等于⊙O的半径.
3
配套练习4
切线的证明:作垂直, 证半径
如图,△ABC为等腰三角形, AB=AC, O是底边BC的中点,
⊙O与腰AB相切于点D. 求证:AC与⊙O相切.
证明:连接OD, OA, 过点O作OE⊥AC于点E.
∵AB=AC, O是底边BC的中点,
∴OA是∠BAC的平分线.
∵⊙O与AB相切于点D, ∴OD⊥AB.
又∵OE⊥AC, ∴OE=OD, 即OE是⊙O的半径,
∴AC与⊙O相切.
4
经过圆外一点作圆的切线,这点和切点之间的线段的长叫做切线长.
4
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
A
P
O
P
A
O
B
∵PA、PB与⊙O分别相切于点A、B
PA = PB
几何语言:
∠APO=∠ BPO
∴
4
配套练习5
3
C
O
连接OA,OB,OC.
∵AC,AB与⊙O相切
∴由切线长定理可得,
∠CAO=∠BAO=(180°-60°)÷2=60°
在Rt△OBA中:
OB=tan∠BAO AB=
5
5
5
2
配套练习 6
5
r
r
r
5
配套练习 7
谢谢观看
3
配套练习3
3
3
3
直线与圆的位置关系
考点梳理
直线和圆的位置关系
1
切线的性质
2
切线的判定
3
切线长定理
4
内心、外心
5
1
直线与圆的位置关系
—— 用公共点的个数来区分
1
.O
l
.O
叫做直线和圆相离.
直线和圆没有公共点,
l
直线和圆有唯一的公共点,
叫做直线和圆相切.
唯一的公共点叫切点.
.O
l
直线和圆有两个公共点,
叫做直线和圆相交.
这时的直线叫做圆的割线 .
.A
.B
切点
割线
切线
这时的直线叫切线,
A
直线与圆的位置关系
—— 数量特征
1
r
d
直线 l 和⊙O相交
O
d
r
直线 l 和⊙O相切
O
l
d < r
d = r
d:圆心到直线的距离
r :半径
d
r
直线 l 和⊙O相离
O
l
d > r
l
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_______________________的关系来判断.
(在实际应用中,常采用第二种方法判定)
两
直线与圆的公共点
圆心到直线的距离与半径
小结
答案
(3)d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
配套练习1
2
切线与圆有唯一的公共点
2
圆心到切线的距离等于圆的半径
切线垂直于过切点的半径
r
O
l
切线
切点
A
配套练习2
70°
1
2
3
连接OA,OB
3
3
圆心到直线的距离等于圆的半径,则此直线是圆的切线.
r
O
l
切线
切点
A
1
2
经过圆上一点,且与过这一点的半径①垂直②的直线是圆的切线。
题型一:连半径, 证垂直
题型二:作垂直, 证半径
3
题型一:连半径, 证垂直
证明某直线是圆的切线时, 如果已知直线与圆有公共点, 那么可作出经过该点的半径, 证明直线垂直于该半径,则可证明是切线, 即“有交点, 连半径, 证垂直”.
3
配套练习3
切线的证明:连半径, 证垂直
如图以△ABC的BC边上一 点O为圆心的圆经过A, B两点, 且与BC边交于点E,
D为BE下方的半圆的中点, 连接AD交BC于点F, 且 AC=FC. 求证:AC是⊙O的切线.
证明:如图, 连接OA, OD.
∵OA=OD, ∴∠OAD=∠ODA.
∵D为BE下方的半圆的中点, ∴OD⊥BE,
∴∠ODA+∠OFD=90° .
∵AC=FC, ∴∠FAC=∠AFC.
又∵∠OFD=∠AFC, ∴∠OFD=∠FAC, ∴∠OAD+∠FAC=∠ODA+∠OFD=90°, 即∠OAC=90° .
又∵OA是⊙O的半径, ∴AC是⊙O的切线.
3
题型二:作垂直, 证半径
证明某直线是圆的切线时, 如果已知直线与圆有公共点, 那么可作出经过该点的半径, 证明直线垂直于该半径, 则可证明是切线,即“有交点, 连半径, 证垂直”.
3
配套练习4
切线的证明:作垂直, 证半径
如图,△ABC为等腰三角形, AB=AC, O是底边BC的中点,
⊙O与腰AB相切于点D. 求证:AC与⊙O相切.
分析 AC与⊙O的交点不明确,所以可过圆心O作OE⊥AC于点E, 证明OE的长等于⊙O的半径.
3
配套练习4
切线的证明:作垂直, 证半径
如图,△ABC为等腰三角形, AB=AC, O是底边BC的中点,
⊙O与腰AB相切于点D. 求证:AC与⊙O相切.
证明:连接OD, OA, 过点O作OE⊥AC于点E.
∵AB=AC, O是底边BC的中点,
∴OA是∠BAC的平分线.
∵⊙O与AB相切于点D, ∴OD⊥AB.
又∵OE⊥AC, ∴OE=OD, 即OE是⊙O的半径,
∴AC与⊙O相切.
4
经过圆外一点作圆的切线,这点和切点之间的线段的长叫做切线长.
4
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
A
P
O
P
A
O
B
∵PA、PB与⊙O分别相切于点A、B
PA = PB
几何语言:
∠APO=∠ BPO
∴
4
配套练习5
3
C
O
连接OA,OB,OC.
∵AC,AB与⊙O相切
∴由切线长定理可得,
∠CAO=∠BAO=(180°-60°)÷2=60°
在Rt△OBA中:
OB=tan∠BAO AB=
5
5
5
2
配套练习 6
5
r
r
r
5
配套练习 7
谢谢观看
3
配套练习3
3
3
3
