24.3正多边形和圆 人教版数学九年级上册 课件(17张ppt)
文档属性
| 名称 | 24.3正多边形和圆 人教版数学九年级上册 课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 183.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
24.3 正多边形和圆
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
自学指导
思考下列问题:
1、为什么将圆分成相等的5段弧,做出的五边形是正五边形?
2、什么是正多边形的中心?什么是正多边形的半径、中心角、边心距?举例说明?
3、n边形的内角和的计算公式?正n边形的一个内角的度数是多少度?中心角是多少度?中心角与外角有什么关系?
以中心为圆心,边心距为半径的圆与各边有何位置关系
E
F
C
D
.
.
O
中心角
半径R
边心距r
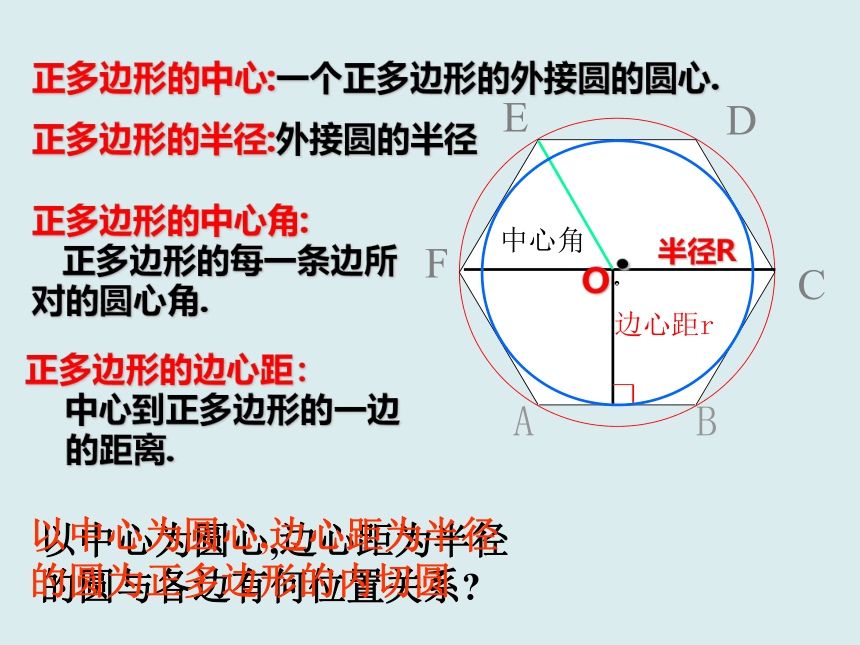
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边
的距离.
A
B
以中心为圆心,边心距为半径的圆为正多边形的内切圆
1.各边相等的圆内接多边形是正多边形( )
2.各边相等的圆外切多边形是正多边形( )
3.各角相等的圆内接多边形是正多边形( )
4.各角相等的圆外切多边形是正多边形( )
填空:
课堂练习
⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。
边心距
内切
判断:
E
F
C
D
.
.
O
中心角
A
B
G
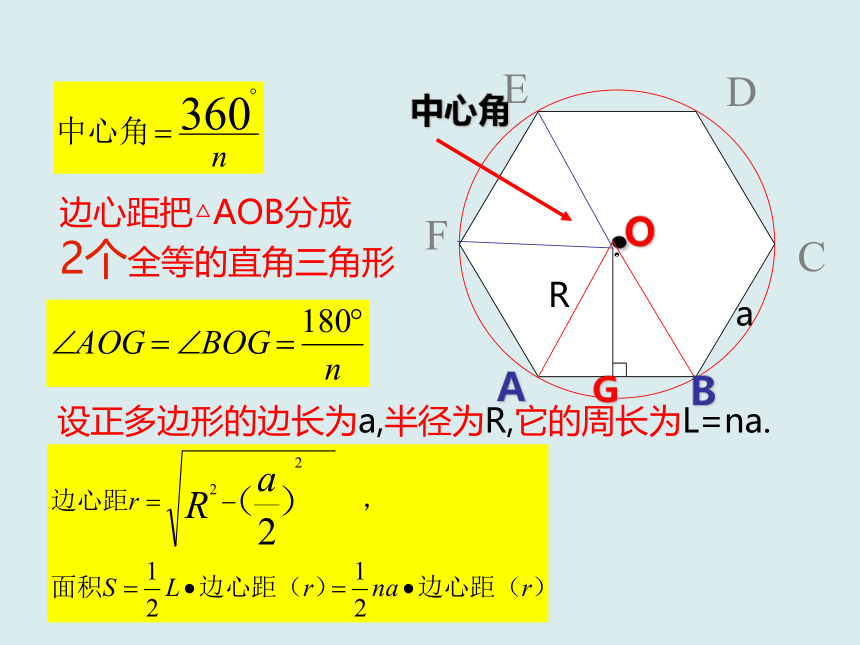
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
1. ∠AOB叫做正五边形ABCDE的 角,
它的度数是
D
E
A
B
C
.O
F
中心
72度
课堂练习
2. 正多边形的一边所对的中心角与该多边形的一个内角的关系为( )
B
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
3. 如图所示,正六边形ABCDEF内接于⊙O ,则∠ADB的度数是( )
A.60° B.45°
C.30° D.22.5°
C
4. 已知圆内接正三角形的边心距为1,则这个三角形的面积( )
A. B. C. D.
B
5.如图,正六边形ABCDEF内接于 ⊙O ,半径为4,求这个正六边形的边心距OM 的长.
解析:连接OB,OC
∵正六边形ABCDEF内接于 ⊙O,
∴中心角∠BOC= =60° ,
∵OB=OC,∴ △BOC是等边三角形.
∵OB⊥BC,
∴ ∠BOM= ∠BOC =30°,
∴ BM= OB = ×4=2 ,
∴
6. 分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
连接OB,则OB=R
在Rt△OBD中,∠OBD=30°,
在Rt△ABD中,∠BAD=30°,
·
A
B
C
D
O
∴AB=
∴S△ABC=
边心距=OD=
解:连接OB,OC 作OE⊥BC垂足为E,
在Rt△OBE中为等腰直角三角形
·
A
B
C
D
O
E
∠OEB=90° ∠OBE= ∠ BOE=45°
课堂小结
本节课你学会了什么?还有什么疑惑吗?
1、正方形ABCD的外接圆圆心O叫做正方形ABCD的______.
2、正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
3、若正六边形的边长为1,那么正六边形的中心角是____度,半径是___,边心距是 ,它的每一个内角是______.
4、正n边形的一个外角度数与它的______角的度数相等.
当堂测评
中心
边心距
60
1
120°
中心
5.正多边形一定是 对称图形,一个正n边形共有 条对称轴,每条对称轴都通过 ;如果一个正n边形是中心对称图形,n一定是 数.
6.将一个正五边形绕它的中心旋转,至少要旋转 度,才能与原来的图形位置重合.
7.两个正三角形的内切圆的半径分别为12和18,则它们的周长之比为 ,面积之比为 .
轴
n
中心
偶
72
2﹕3
4﹕9
8.下列说法中正确的是( )
A.平行四边形是正四边形 B. 矩形是正四边形
C. 菱形是正四边形 D. 正方形是正四边形
9. 下列命题中,真命题的个数是( )
①各边都相等的多边形是正多边形;
②各角都相等的多边形是正多边形;
③正多边形一定是中心对称图形;
④边数相同的正多边形一定全等.
A.1 B.2 C. 3 D. 4
D
A
10.已知正n边形的一个外角与一个内角的比为1﹕3,则n等于( )
A. 4 B. 6 C. 8 D. 12
11. 如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
C
B
24.3 正多边形和圆
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
自学指导
思考下列问题:
1、为什么将圆分成相等的5段弧,做出的五边形是正五边形?
2、什么是正多边形的中心?什么是正多边形的半径、中心角、边心距?举例说明?
3、n边形的内角和的计算公式?正n边形的一个内角的度数是多少度?中心角是多少度?中心角与外角有什么关系?
以中心为圆心,边心距为半径的圆与各边有何位置关系
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:
正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边
的距离.
A
B
以中心为圆心,边心距为半径的圆为正多边形的内切圆
1.各边相等的圆内接多边形是正多边形( )
2.各边相等的圆外切多边形是正多边形( )
3.各角相等的圆内接多边形是正多边形( )
4.各角相等的圆外切多边形是正多边形( )
填空:
课堂练习
⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。
边心距
内切
判断:
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
1. ∠AOB叫做正五边形ABCDE的 角,
它的度数是
D
E
A
B
C
.O
F
中心
72度
课堂练习
2. 正多边形的一边所对的中心角与该多边形的一个内角的关系为( )
B
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
3. 如图所示,正六边形ABCDEF内接于⊙O ,则∠ADB的度数是( )
A.60° B.45°
C.30° D.22.5°
C
4. 已知圆内接正三角形的边心距为1,则这个三角形的面积( )
A. B. C. D.
B
5.如图,正六边形ABCDEF内接于 ⊙O ,半径为4,求这个正六边形的边心距OM 的长.
解析:连接OB,OC
∵正六边形ABCDEF内接于 ⊙O,
∴中心角∠BOC= =60° ,
∵OB=OC,∴ △BOC是等边三角形.
∵OB⊥BC,
∴ ∠BOM= ∠BOC =30°,
∴ BM= OB = ×4=2 ,
∴
6. 分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
连接OB,则OB=R
在Rt△OBD中,∠OBD=30°,
在Rt△ABD中,∠BAD=30°,
·
A
B
C
D
O
∴AB=
∴S△ABC=
边心距=OD=
解:连接OB,OC 作OE⊥BC垂足为E,
在Rt△OBE中为等腰直角三角形
·
A
B
C
D
O
E
∠OEB=90° ∠OBE= ∠ BOE=45°
课堂小结
本节课你学会了什么?还有什么疑惑吗?
1、正方形ABCD的外接圆圆心O叫做正方形ABCD的______.
2、正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
3、若正六边形的边长为1,那么正六边形的中心角是____度,半径是___,边心距是 ,它的每一个内角是______.
4、正n边形的一个外角度数与它的______角的度数相等.
当堂测评
中心
边心距
60
1
120°
中心
5.正多边形一定是 对称图形,一个正n边形共有 条对称轴,每条对称轴都通过 ;如果一个正n边形是中心对称图形,n一定是 数.
6.将一个正五边形绕它的中心旋转,至少要旋转 度,才能与原来的图形位置重合.
7.两个正三角形的内切圆的半径分别为12和18,则它们的周长之比为 ,面积之比为 .
轴
n
中心
偶
72
2﹕3
4﹕9
8.下列说法中正确的是( )
A.平行四边形是正四边形 B. 矩形是正四边形
C. 菱形是正四边形 D. 正方形是正四边形
9. 下列命题中,真命题的个数是( )
①各边都相等的多边形是正多边形;
②各角都相等的多边形是正多边形;
③正多边形一定是中心对称图形;
④边数相同的正多边形一定全等.
A.1 B.2 C. 3 D. 4
D
A
10.已知正n边形的一个外角与一个内角的比为1﹕3,则n等于( )
A. 4 B. 6 C. 8 D. 12
11. 如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
C
B
同课章节目录
