天津市天津一中2013届高三零月试卷 理科数学
文档属性
| 名称 | 天津市天津一中2013届高三零月试卷 理科数学 | 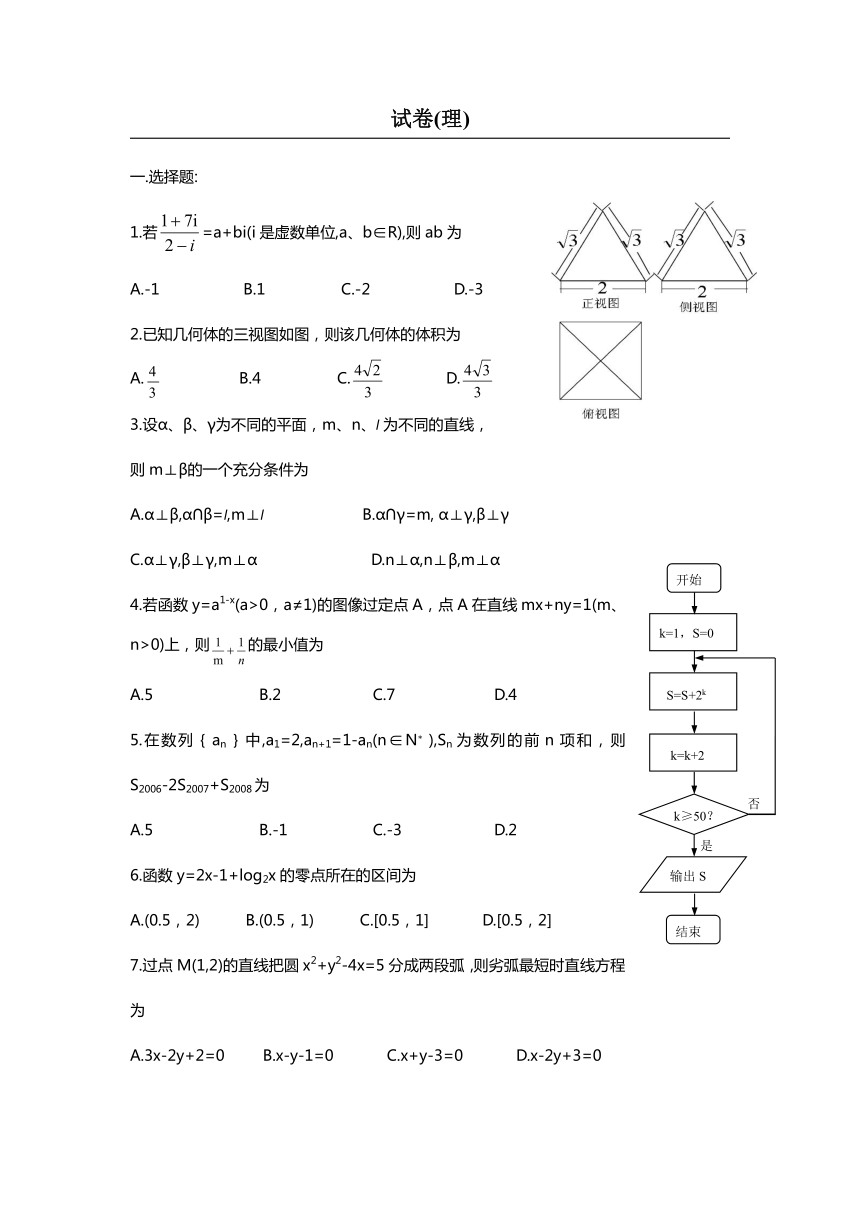 | |
| 格式 | zip | ||
| 文件大小 | 81.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-25 19:04:12 | ||
图片预览




文档简介
试卷(理)
一.选择题:
1.若=a+bi(i是虚数单位,a、b∈R),则ab为
A.-1 B.1 C.-2 D.-3
2.已知几何体的三视图如图,则该几何体的体积为
A. B.4 C. D.
3.设α、β、γ为不同的平面,m、n、l为不同的直线,
则m⊥β的一个充分条件为
A.α⊥β,α∩β=l,m⊥l B.α∩γ=m, α⊥γ,β⊥γ
C.α⊥γ,β⊥γ,m⊥α D.n⊥α,n⊥β,m⊥α
4.若函数y=a1-x(a>0,a≠1)的图像过定点A,点A在直线mx+ny=1(m、n>0)上,则的最小值为
A.5 B.2 C.7 D.4
5.在数列{an}中,a1=2,an+1=1-an(n∈N? ),Sn为数列的前n项和,则S2006-2S2007+S2008为
A.5 B.-1 C.-3 D.2
6.函数y=2x-1+log2x的零点所在的区间为
A.(0.5,2) B.(0.5,1) C.[0.5,1] D.[0.5,2]
7.过点M(1,2)的直线把圆x2+y2-4x=5分成两段弧,则劣弧最短时直线方程为
A.3x-2y+2=0 B.x-y-1=0 C.x+y-3=0 D.x-2y+3=0
8.执行如图所示的程序框图,输出的S值为
A.(425-1) B.(426-1) C.250-1 D.251-1
二.填空题:
9.二项式展开式中x2系数为60,则实数a的值=_____.
10.已知5cos(45o+x)=3,则sin2x= .
11.?ABC中,O为中线AM上一个动点,若AM=2,则的最小值= .
12.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则双曲线的离心率= .
13.极坐标系中,曲线ρ=10cosθ和直线3ρcosθ-4ρsinθ-30=0交于A、B两
点,则线段AB的长= .
14.已知PA是圆O的切线,切点为A,PO交圆O于B、C 两点,
AC=,∠PAB=30o,则线段PB的长= .
三.解答题:
15.已知?ABC中,A、B、C分别为三个内角,a、b、c为所对边,2(sin2A- sin2C)=(a-b)sinB, ?ABC的外接圆半径为,(1)求角C;(2)求?ABC面积S的最大值.
16.右图为一多面体,其底面ABCD为正方形,PD⊥平面ABCD,CE//DP,且PD=2CE,(1)求证:BE//平面PDA;(2)若N为线段PB的中点,求证:EN⊥平面PDB;(3)若PD=AD,求平面PBE与平面ABCD所成的二面角的余弦值.
17.设有编号为1,2,3,……,n的n个学生,编号为1,2,3,……,n的n个座位.规定每个学生坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.(1)求n的值;(2)求随机变量ξ的概率分布列和数学期望.
18.数列{an}的前n项和Sn,点(an,Sn)在直线y=2x-3n上,(1)若数列{an+c}为等比数列,求常数c的值;(2)求数列{an}的通项公式;(3) 数列{an}中是否存在三项,使它们构成等差数列?若存在,求出一组适合条件的项;若不存在,说明理由.
19.已知椭圆C1:的离心率为,直线l: y=x+2与以原点为圆心,以椭圆的短半轴长为半径的圆相切.(1)求椭圆C1的方程;(2)设椭圆C1的左、右焦点F1、F2,直线l1过点F1且垂直于椭圆长轴,动直线l2垂直l1于点P,线段P F2的垂直平分线交l2于点M,求点M的轨迹C2方程;(3)设C2与x轴交于Q点,不同的两点R、S在C2上,且满足=0.,求∣QS∣的取值范围.
20.已知函数f(x)=ax4lnx+bx4-c (x>0),在x = 1处取得极值-3-c,其中a,b,c为常数.(1)试确定a,b的值;(2)讨论函数f(x)的单调区间;(3)若对任意x>0,不等式f(x)+2c2≥0恒成立,求c的取值范围.
答案:
一、选择题:
1、D 2、C 3、D 4、D 5、C 6、B 7、D 8、A
二、填空题:
9、±2 10、 11、-2 12、3 13、8 14、1
三、解答题:
15、解:(1)
a2-c2=ab-b2即a2+b2-c2=ab
∴2abcosC=ab cosC= c=
(2)SΔABC=absinC
=absin=
=
=
=3sinAcosA+sin2A
=sin2A+(1-cos2A)
=sin2A-cos2A+
=sin(2A-)+
当2A-=
即A=时,SΔABCmax=
16、解:(1)取PD中点F,则FDEC,∴□EFDC ∴EFCDAB
∴□EFAB ∴ BE//AF ∴BE//平面PDA
AF面PDA
(2)设AC∩BD=O则NOCE ∴□NOCE ∴CO//EN
∵ PD⊥面ABCD ∴ PD⊥NE ∴NE⊥平面PDB
PD//CE//NO BD⊥NE
(3)设平面PBE与平面ABCD所夹角为
∵PD⊥平面ABCD于D,CE⊥平面ABCD于C,∴
SΔBDC=,在ΔPBE中,PB=2a,BE=,PE=
SΔPBE= ∴
17、解:(1)由ξ=2可知有n-2学生对位,2个错位,选n-2个学生对位
∴,∴n=4
(2)P(ξ=0)=,P(ξ=2)==
P(ξ=3)=,P(ξ=4)=
Eξ
ξ
0
2
3
4
P
18、把(an;Sn)代入y=2x-3n中,
Sn=2an-3n
Sn-1=2an-1-3(n-1) (n≥2)
两式相减:an=2an-1+3
即an+3=2(an-1+3)
∴c=3,当n=1时,a1=3
(2)由{an+3}是首项6公比2的等比数列
∴an+3=6·2n-1
∴an=3·2n-3(n∈N*)
(3)设假设存在
则
即
事实上,,
∴ 0< ∴
∴假设存在不成立
∴不存在
19、解:(1)由e=可知 a= ∴2a2=3b2
a2=b2+c2
由y=x+2与(x2+y2=b2)相切
b= ∴ b= 为椭圆C1的方程
a=
(2)F1(-1,0),F2(1,0)由已知可知MF2=MP
即点M到点F2距离等于点M到直线l1:x=-1的距离
点M是焦点为F2渐近线为x=-1的抛物线,p=2 ∴y2=4x
(3)由(2)可知Q点为原点O,设R(x1,y1) ,S(x2,y2)
,由
即x1(x2-x1)+y1(y2-y1)=0
x1x2-+y1y2-=0,
x1x2--4
,当且仅当x1=2时,x2≥16
而|QS|=|OS|=
=≥
∴|QS|∈[815,+∞)
另:设直线OR方程 y=kx R(),不妨设k>0
y2=4x
直线RS方程 y-=-
y2=4x
∴ |QS|=|OS|=4
(k+)2≥4
20、解:(1)f ’(x)=4ax3lnx+ax3+4bx3 由 f ’(1)=0
f(1)=-3-c
即
(2)f(x)=12x4lnx-3x4-c
f ’(x)=48x3lnx+12x3-12x3=48x3lnx,(x>0)
f(x)增区间(1,+∞),减区间(0,1)
(3)由对x>0,f(x)+2c2≥0成立
即:12x4lnx-3x4-c+2c2≥0对x∈R成立
即:c-2c2≤12x4lnx-3x4对x∈R成立
必须满足c-2c2≤{12x4lnx-3x4}min
设g(x)=12x4lnx-3x4
g’(x)=48x3lnx,如图
当x=1时,g(x)min=g(1)=-3
∴c-2c2≤3 即2c2-c-3≥0
∴c≤-1或c≥
一.选择题:
1.若=a+bi(i是虚数单位,a、b∈R),则ab为
A.-1 B.1 C.-2 D.-3
2.已知几何体的三视图如图,则该几何体的体积为
A. B.4 C. D.
3.设α、β、γ为不同的平面,m、n、l为不同的直线,
则m⊥β的一个充分条件为
A.α⊥β,α∩β=l,m⊥l B.α∩γ=m, α⊥γ,β⊥γ
C.α⊥γ,β⊥γ,m⊥α D.n⊥α,n⊥β,m⊥α
4.若函数y=a1-x(a>0,a≠1)的图像过定点A,点A在直线mx+ny=1(m、n>0)上,则的最小值为
A.5 B.2 C.7 D.4
5.在数列{an}中,a1=2,an+1=1-an(n∈N? ),Sn为数列的前n项和,则S2006-2S2007+S2008为
A.5 B.-1 C.-3 D.2
6.函数y=2x-1+log2x的零点所在的区间为
A.(0.5,2) B.(0.5,1) C.[0.5,1] D.[0.5,2]
7.过点M(1,2)的直线把圆x2+y2-4x=5分成两段弧,则劣弧最短时直线方程为
A.3x-2y+2=0 B.x-y-1=0 C.x+y-3=0 D.x-2y+3=0
8.执行如图所示的程序框图,输出的S值为
A.(425-1) B.(426-1) C.250-1 D.251-1
二.填空题:
9.二项式展开式中x2系数为60,则实数a的值=_____.
10.已知5cos(45o+x)=3,则sin2x= .
11.?ABC中,O为中线AM上一个动点,若AM=2,则的最小值= .
12.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则双曲线的离心率= .
13.极坐标系中,曲线ρ=10cosθ和直线3ρcosθ-4ρsinθ-30=0交于A、B两
点,则线段AB的长= .
14.已知PA是圆O的切线,切点为A,PO交圆O于B、C 两点,
AC=,∠PAB=30o,则线段PB的长= .
三.解答题:
15.已知?ABC中,A、B、C分别为三个内角,a、b、c为所对边,2(sin2A- sin2C)=(a-b)sinB, ?ABC的外接圆半径为,(1)求角C;(2)求?ABC面积S的最大值.
16.右图为一多面体,其底面ABCD为正方形,PD⊥平面ABCD,CE//DP,且PD=2CE,(1)求证:BE//平面PDA;(2)若N为线段PB的中点,求证:EN⊥平面PDB;(3)若PD=AD,求平面PBE与平面ABCD所成的二面角的余弦值.
17.设有编号为1,2,3,……,n的n个学生,编号为1,2,3,……,n的n个座位.规定每个学生坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.(1)求n的值;(2)求随机变量ξ的概率分布列和数学期望.
18.数列{an}的前n项和Sn,点(an,Sn)在直线y=2x-3n上,(1)若数列{an+c}为等比数列,求常数c的值;(2)求数列{an}的通项公式;(3) 数列{an}中是否存在三项,使它们构成等差数列?若存在,求出一组适合条件的项;若不存在,说明理由.
19.已知椭圆C1:的离心率为,直线l: y=x+2与以原点为圆心,以椭圆的短半轴长为半径的圆相切.(1)求椭圆C1的方程;(2)设椭圆C1的左、右焦点F1、F2,直线l1过点F1且垂直于椭圆长轴,动直线l2垂直l1于点P,线段P F2的垂直平分线交l2于点M,求点M的轨迹C2方程;(3)设C2与x轴交于Q点,不同的两点R、S在C2上,且满足=0.,求∣QS∣的取值范围.
20.已知函数f(x)=ax4lnx+bx4-c (x>0),在x = 1处取得极值-3-c,其中a,b,c为常数.(1)试确定a,b的值;(2)讨论函数f(x)的单调区间;(3)若对任意x>0,不等式f(x)+2c2≥0恒成立,求c的取值范围.
答案:
一、选择题:
1、D 2、C 3、D 4、D 5、C 6、B 7、D 8、A
二、填空题:
9、±2 10、 11、-2 12、3 13、8 14、1
三、解答题:
15、解:(1)
a2-c2=ab-b2即a2+b2-c2=ab
∴2abcosC=ab cosC= c=
(2)SΔABC=absinC
=absin=
=
=
=3sinAcosA+sin2A
=sin2A+(1-cos2A)
=sin2A-cos2A+
=sin(2A-)+
当2A-=
即A=时,SΔABCmax=
16、解:(1)取PD中点F,则FDEC,∴□EFDC ∴EFCDAB
∴□EFAB ∴ BE//AF ∴BE//平面PDA
AF面PDA
(2)设AC∩BD=O则NOCE ∴□NOCE ∴CO//EN
∵ PD⊥面ABCD ∴ PD⊥NE ∴NE⊥平面PDB
PD//CE//NO BD⊥NE
(3)设平面PBE与平面ABCD所夹角为
∵PD⊥平面ABCD于D,CE⊥平面ABCD于C,∴
SΔBDC=,在ΔPBE中,PB=2a,BE=,PE=
SΔPBE= ∴
17、解:(1)由ξ=2可知有n-2学生对位,2个错位,选n-2个学生对位
∴,∴n=4
(2)P(ξ=0)=,P(ξ=2)==
P(ξ=3)=,P(ξ=4)=
Eξ
ξ
0
2
3
4
P
18、把(an;Sn)代入y=2x-3n中,
Sn=2an-3n
Sn-1=2an-1-3(n-1) (n≥2)
两式相减:an=2an-1+3
即an+3=2(an-1+3)
∴c=3,当n=1时,a1=3
(2)由{an+3}是首项6公比2的等比数列
∴an+3=6·2n-1
∴an=3·2n-3(n∈N*)
(3)设假设存在
则
即
事实上,,
∴ 0< ∴
∴假设存在不成立
∴不存在
19、解:(1)由e=可知 a= ∴2a2=3b2
a2=b2+c2
由y=x+2与(x2+y2=b2)相切
b= ∴ b= 为椭圆C1的方程
a=
(2)F1(-1,0),F2(1,0)由已知可知MF2=MP
即点M到点F2距离等于点M到直线l1:x=-1的距离
点M是焦点为F2渐近线为x=-1的抛物线,p=2 ∴y2=4x
(3)由(2)可知Q点为原点O,设R(x1,y1) ,S(x2,y2)
,由
即x1(x2-x1)+y1(y2-y1)=0
x1x2-+y1y2-=0,
x1x2--4
,当且仅当x1=2时,x2≥16
而|QS|=|OS|=
=≥
∴|QS|∈[815,+∞)
另:设直线OR方程 y=kx R(),不妨设k>0
y2=4x
直线RS方程 y-=-
y2=4x
∴ |QS|=|OS|=4
(k+)2≥4
20、解:(1)f ’(x)=4ax3lnx+ax3+4bx3 由 f ’(1)=0
f(1)=-3-c
即
(2)f(x)=12x4lnx-3x4-c
f ’(x)=48x3lnx+12x3-12x3=48x3lnx,(x>0)
f(x)增区间(1,+∞),减区间(0,1)
(3)由对x>0,f(x)+2c2≥0成立
即:12x4lnx-3x4-c+2c2≥0对x∈R成立
即:c-2c2≤12x4lnx-3x4对x∈R成立
必须满足c-2c2≤{12x4lnx-3x4}min
设g(x)=12x4lnx-3x4
g’(x)=48x3lnx,如图
当x=1时,g(x)min=g(1)=-3
∴c-2c2≤3 即2c2-c-3≥0
∴c≤-1或c≥
同课章节目录
