北师大版八年级数学下册6.1平行四边形的性质(一)课件(38张ppt)
文档属性
| 名称 | 北师大版八年级数学下册6.1平行四边形的性质(一)课件(38张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 08:11:16 | ||
图片预览








文档简介
(共38张PPT)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
美丽的家园,我们要好好的利用和保护她
运用广泛
美观别致
随处可见
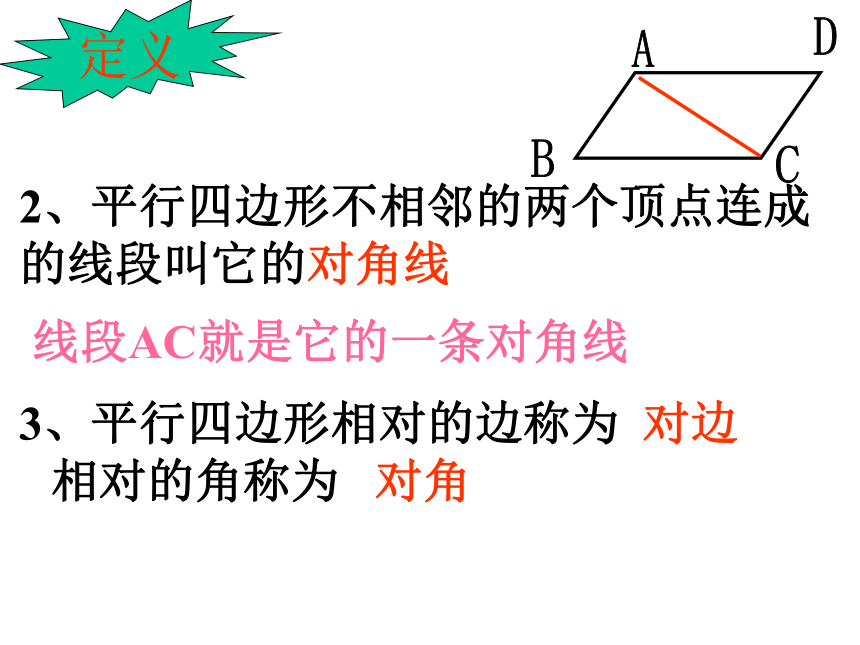
定义
B
D
C
A
1.我们知道,有两组对边分别平行的四边形叫做平行四边形.
概念引入
如图四边形ABCD是平行四边形,
记作: ABCD
注意字母的书写顺序哦:
1.按顺时针,如
2.按逆时针,如
ABCD
ADCB
定义
定义
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线
线段AC就是它的一条对角线
3、平行四边形相对的边称为 对边 相对的角称为 对角
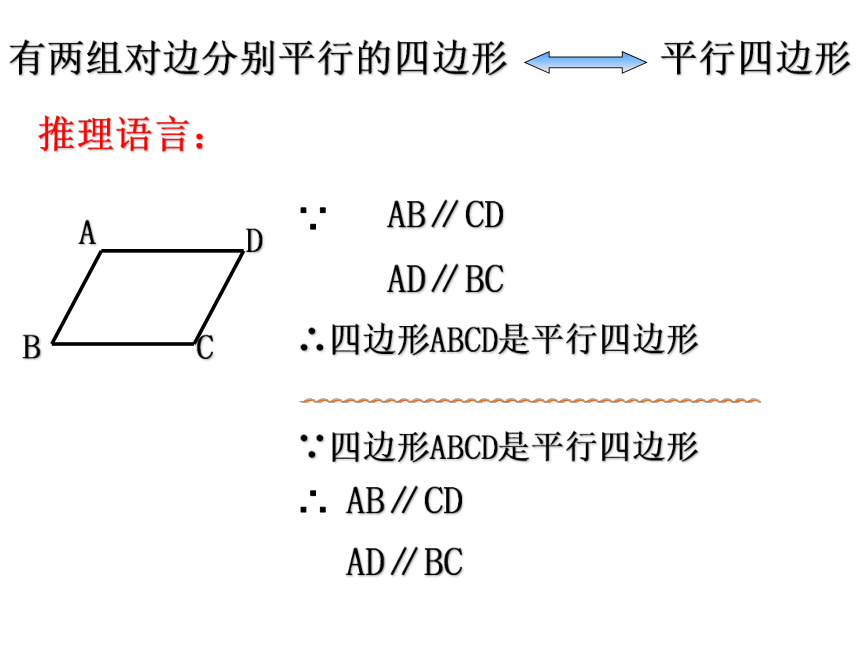
平行四边形
有两组对边分别平行的四边形
推理语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
AB∥CD
AD∥BC
∵
A
D
B
C
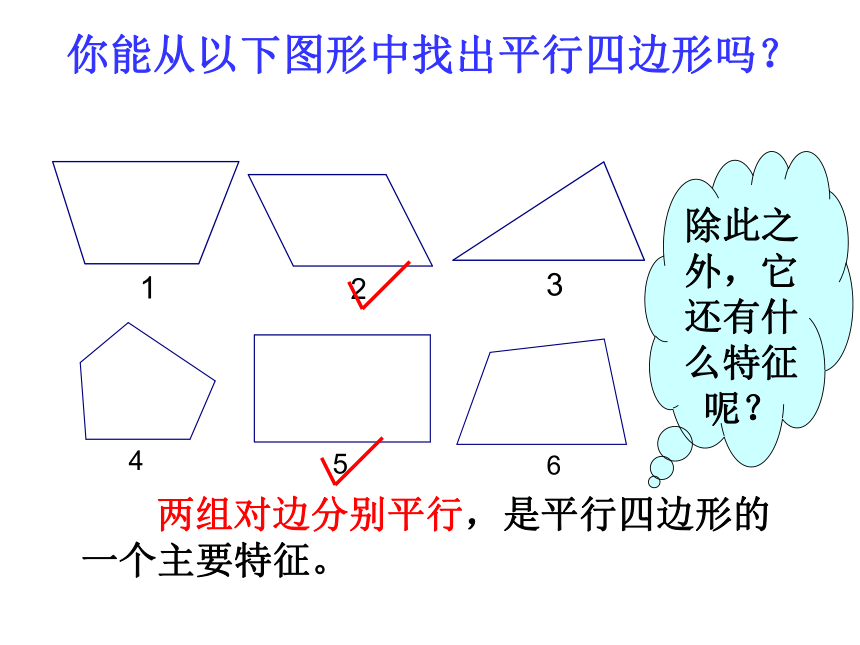
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
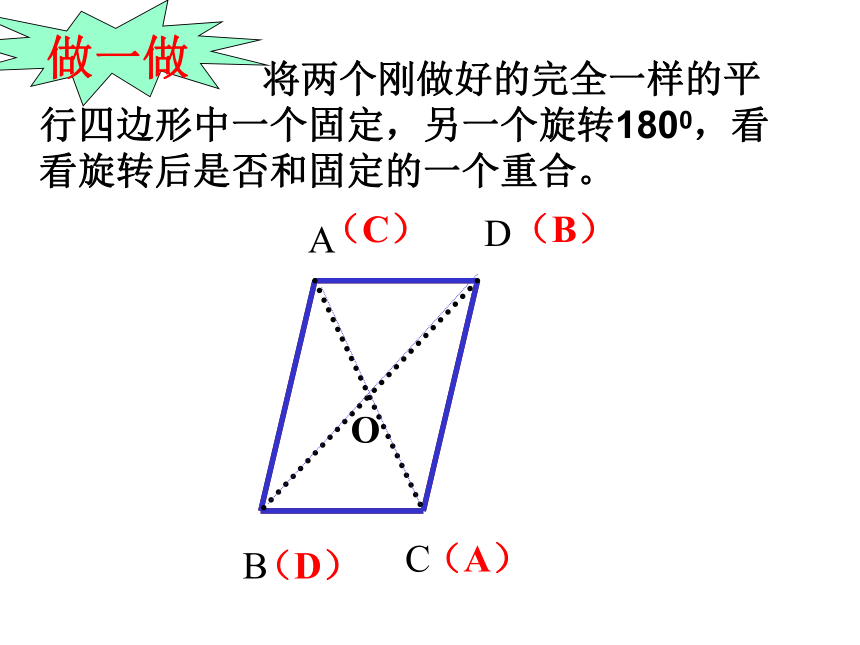
将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
O
A
B
C
D
(C)
(A)
(B)
(D)
做一做
同桌讨论:观察、猜测平行四边形
有哪些性质?
D
B
C
A
实验报告:
研究对象
研究结果
几何表示
对边
对角
平行且相等
AB∥CD AD∥BC
AB=CD AD=BC
相等
∠A=∠C ,∠ B=∠D
我们发现,平行四边形绕对角线的交点旋转180度后能与原图重合,所以说平行四边形是中心对称图形,对角线的交点就是对称中心.
平行四边形的性质:
性质1:平行四边形的对边相等。
A
B
C
D
性质2:平行四边形的对角相等。
A
B
C
D
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D。
∵四边形ABCD是平行四边形∴AB=CD,BC=AD。
你能证明它们吗?
56°
124°
56°
已知 ABCD中,∠BAD= 56° 则:∠BCD=
124°
56°
124°
124°
∠B =
∴ ∠BAD+ ∠B = 180°
∵ AD∥BC
∠D=
结论:平行四边形的邻角互补
例1如图,在 ABCD中,已知∠A=40°,求其他各个内角的度数.
解 在?ABCD中,
∠D=∠B, ∠C=∠A=40°(平行四边形的对角相等).
又∵ AD∥BC,
∴ ∠B=180°-∠A=180°-40°=140°,(两直线平行,同旁内角互补,即平行四边形的邻角互补.)
∴ ∠D=∠B=140°.
练习1.已知 ABCD中,∠A=120°,
你能求出其余各内角的度数吗?
说说你的理由。
120°
解:在 ABCD中, ∠C=∠ A=120°;
∠B=∠D =180°- ∠A=180°- 120°= 60°
(两直线平行,同旁内角互补)
补充题1.已知 ABCD中,∠1=80°,
你能求出其他各角的度数吗?
说说你的理由。
1
解:在 ABCD中, ∠ABC=∠D=1 80°- ∠1= 180°- 80°= 100°
∠A=∠C= 180°- ∠D = 180°- 100°= 80°(两 直线平行,同旁内角互补)
或∠A=∠C= ∠1=80°(两直线平行,内错角相等)
解:在 ABCD中, ∠ABC=∠D=1 80°- ∠1= 180°- 80°= 100°
∠A=∠C= 180°- ∠D = 180°- 100°= 80°(两 直线平行,同旁内角互补)
或∠A=∠C= ∠1=80°(两直线平行,内错角相等)
补充题1.已知 ABCD中,∠1=80°,
你能求出其他各角的度数吗?
说说你的理由。
1
解:在 ABCD中, ∠ABC=∠D=1 80°- ∠1= 180°- 80°= 100°
∠A=∠C= 180°- ∠D = 180°- 100°= 80°(两 直线平行,同旁内角互补)
或∠A=∠C= ∠1=80°(两直线平行,内错角相等)
补充题1.已知 ABCD中,∠1=80°,
你能求出其他各角的度数吗?
说说你的理由。
1
2.已知 ABCD中,AC平分∠BAD,
∠BAC=25°,
你能求出其各角的度数吗?
说说你的理由。
25°
解:在平行四边形ABCD中,
∵ AC平分∠BAD, ∠BAC=25°
∴∠DAC= ∠DCB =2 ∠BAC=2×25°= 50°;
∠B=∠D= 180°- 50°= 130°.
3.已知 ABCD中,
∠A+∠C=100°,
你能求出各角的度数吗?
说说你的理由。
解:∵在平行四边形ABCD中, ∠A+∠C=100°,
∴ ∠A= ∠C= 50°; ∠B=∠D= 180- 50°= 130°.
A
D
C
B
8
例2 如图,已知 中,AB=8,
周长等于24,求其余三条边的长.
ABCD
解:在 中, AD=BC, CD=AB=8;
因为AD+BC+CD+AB=24,
所以AD+BC=24-CD-AB=24-8-8=8,
所以AD=BC=8/2=4.
ABCD
D
练习2 如图,已知 中,AB=5,
BC=3, 你能求 的周长吗
解:因为在 中, CD=AB=5,AD=BC=3,所以所求周长=CD+AB+AD+BC=5+5+3+3=16
ABCD
ABCD
A
D
C
B
5
3
ABCD
应用巩固 深化提高
(1) 已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
练一练:
选择:平行四边形具有而一般四边形
不一定具有的特征是( )
A、不稳定性 B、对边平行且相等
C、内角和为360度 D、外角和为360度
B
在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:
120°、
60°、
120°
已知在 ABCD中,AD+DC=13,求它的周长
A
B
C
D
13
26
总结:平行四边形两邻边的和的两倍等于周长
可要细心哟
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
A
B
C
D
80°
100°
80°
100°
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
让我们大家一起来想!
平行四边形的性质
边
平行四边形的对边平行且相等;
角
平行四边形的邻角互补。
B
D
C
A
∵四边形ABCD是
∴ AB∥CD, AD∥BC
AB = CD, AD= BC
∵四边形ABCD是
∴ ∠A=∠C, ∠B=∠D
∵ AB∥CD
∴ ∠A+∠D=1800, ∠B+∠C=1800
平行四边形的对角相等;
O
平行四边形是中心对称图形
如右图,AB=AC,且AB=5,从等腰三角形底边上任一点,分别作两腰的平行线,问:
①四边形AEDF是什么图形?为什么?
F
E
B
C
A
D
思考题
10
②图中∠1与∠B大小关系怎样?
为什么? ∠2与∠3呢?
③图中那些线段相等?为什么?
④能否求 AEDF各边长?
但能求周长吗?
1
2
3
AE=DF,ED=AF;
BE=DE,DF=CF
相等
数一数,图中有 个平行四边形。
9
可要细心哟
A
B
C
画一个平行四边形,第四个点可以在哪儿?
请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?
无数种,这些墨线都过对角线的交点
如图,在 ABCD中, ∠B=120°,DE⊥AB,垂足为E,DF⊥BC,垂足为F.求∠ADE,∠EDF,∠FDC的度数.
解:在 ABCD中,
∵∠A=∠C,AD∥BC,
∴∠A+∠B=180°.
∴∠A=180°-∠B=60°.
∴∠C=60°.
∵DE⊥AB,DF⊥BC,
∴∠ADE=∠FDC=90°-∠A=90°-60°=30°.
已知 ABCD的周长为28cm,
AB︰BC=3︰4,求它的各边的长.
解:因为在 中, AB=CD,BC=AD.所以AB+BC+CD+AD=28,即AB+BC=14.由题意得AB︰BC=3︰4,因此可设AB=3k,BC=4k,那么有3k+4k=14,解得k=2,则AB=CD=6cm,BC=AD=8cm.
ABCD
作业1. 如图,在?ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠D与∠DAE分别等于多少度
解:在平行四边形ABCD中, ∠D=∠B=55°;
∵ AE垂直于CD,
∴∠AED= 90°,
∴∠DAE= 90 - ∠D= 90- 55= 35°.
作业3. 在 ABCD 中,
∠A︰∠B=2︰3,求各角的度数.
解:(1)因为∠A、∠B是平行四边形的两个邻角,所以∠A+∠B=180°.又因为∠A︰∠B=2︰3,不妨可设∠A=2k,∠B=3k,那么2k+3k=180°,可以解得k=36°,则∠A=∠C=72°,∠B=∠D=108°.
师生共勉
把一件平凡的事情做好就是不平凡
把一件简单的事情做好就是不简单
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
美丽的家园,我们要好好的利用和保护她
运用广泛
美观别致
随处可见
定义
B
D
C
A
1.我们知道,有两组对边分别平行的四边形叫做平行四边形.
概念引入
如图四边形ABCD是平行四边形,
记作: ABCD
注意字母的书写顺序哦:
1.按顺时针,如
2.按逆时针,如
ABCD
ADCB
定义
定义
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线
线段AC就是它的一条对角线
3、平行四边形相对的边称为 对边 相对的角称为 对角
平行四边形
有两组对边分别平行的四边形
推理语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
AB∥CD
AD∥BC
∵
A
D
B
C
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
将两个刚做好的完全一样的平行四边形中一个固定,另一个旋转1800,看看旋转后是否和固定的一个重合。
O
A
B
C
D
(C)
(A)
(B)
(D)
做一做
同桌讨论:观察、猜测平行四边形
有哪些性质?
D
B
C
A
实验报告:
研究对象
研究结果
几何表示
对边
对角
平行且相等
AB∥CD AD∥BC
AB=CD AD=BC
相等
∠A=∠C ,∠ B=∠D
我们发现,平行四边形绕对角线的交点旋转180度后能与原图重合,所以说平行四边形是中心对称图形,对角线的交点就是对称中心.
平行四边形的性质:
性质1:平行四边形的对边相等。
A
B
C
D
性质2:平行四边形的对角相等。
A
B
C
D
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D。
∵四边形ABCD是平行四边形∴AB=CD,BC=AD。
你能证明它们吗?
56°
124°
56°
已知 ABCD中,∠BAD= 56° 则:∠BCD=
124°
56°
124°
124°
∠B =
∴ ∠BAD+ ∠B = 180°
∵ AD∥BC
∠D=
结论:平行四边形的邻角互补
例1如图,在 ABCD中,已知∠A=40°,求其他各个内角的度数.
解 在?ABCD中,
∠D=∠B, ∠C=∠A=40°(平行四边形的对角相等).
又∵ AD∥BC,
∴ ∠B=180°-∠A=180°-40°=140°,(两直线平行,同旁内角互补,即平行四边形的邻角互补.)
∴ ∠D=∠B=140°.
练习1.已知 ABCD中,∠A=120°,
你能求出其余各内角的度数吗?
说说你的理由。
120°
解:在 ABCD中, ∠C=∠ A=120°;
∠B=∠D =180°- ∠A=180°- 120°= 60°
(两直线平行,同旁内角互补)
补充题1.已知 ABCD中,∠1=80°,
你能求出其他各角的度数吗?
说说你的理由。
1
解:在 ABCD中, ∠ABC=∠D=1 80°- ∠1= 180°- 80°= 100°
∠A=∠C= 180°- ∠D = 180°- 100°= 80°(两 直线平行,同旁内角互补)
或∠A=∠C= ∠1=80°(两直线平行,内错角相等)
解:在 ABCD中, ∠ABC=∠D=1 80°- ∠1= 180°- 80°= 100°
∠A=∠C= 180°- ∠D = 180°- 100°= 80°(两 直线平行,同旁内角互补)
或∠A=∠C= ∠1=80°(两直线平行,内错角相等)
补充题1.已知 ABCD中,∠1=80°,
你能求出其他各角的度数吗?
说说你的理由。
1
解:在 ABCD中, ∠ABC=∠D=1 80°- ∠1= 180°- 80°= 100°
∠A=∠C= 180°- ∠D = 180°- 100°= 80°(两 直线平行,同旁内角互补)
或∠A=∠C= ∠1=80°(两直线平行,内错角相等)
补充题1.已知 ABCD中,∠1=80°,
你能求出其他各角的度数吗?
说说你的理由。
1
2.已知 ABCD中,AC平分∠BAD,
∠BAC=25°,
你能求出其各角的度数吗?
说说你的理由。
25°
解:在平行四边形ABCD中,
∵ AC平分∠BAD, ∠BAC=25°
∴∠DAC= ∠DCB =2 ∠BAC=2×25°= 50°;
∠B=∠D= 180°- 50°= 130°.
3.已知 ABCD中,
∠A+∠C=100°,
你能求出各角的度数吗?
说说你的理由。
解:∵在平行四边形ABCD中, ∠A+∠C=100°,
∴ ∠A= ∠C= 50°; ∠B=∠D= 180- 50°= 130°.
A
D
C
B
8
例2 如图,已知 中,AB=8,
周长等于24,求其余三条边的长.
ABCD
解:在 中, AD=BC, CD=AB=8;
因为AD+BC+CD+AB=24,
所以AD+BC=24-CD-AB=24-8-8=8,
所以AD=BC=8/2=4.
ABCD
D
练习2 如图,已知 中,AB=5,
BC=3, 你能求 的周长吗
解:因为在 中, CD=AB=5,AD=BC=3,所以所求周长=CD+AB+AD+BC=5+5+3+3=16
ABCD
ABCD
A
D
C
B
5
3
ABCD
应用巩固 深化提高
(1) 已知:如图6-3,在平行四边形ABCD中,
E,F 是对角线AC上的两点,且AE=CF.
求证:BE = DF.
证明:∵四边形ABCD是平行四边形
∴AB = CD
AB // CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
练一练:
选择:平行四边形具有而一般四边形
不一定具有的特征是( )
A、不稳定性 B、对边平行且相等
C、内角和为360度 D、外角和为360度
B
在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:
120°、
60°、
120°
已知在 ABCD中,AD+DC=13,求它的周长
A
B
C
D
13
26
总结:平行四边形两邻边的和的两倍等于周长
可要细心哟
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
A
B
C
D
80°
100°
80°
100°
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
让我们大家一起来想!
平行四边形的性质
边
平行四边形的对边平行且相等;
角
平行四边形的邻角互补。
B
D
C
A
∵四边形ABCD是
∴ AB∥CD, AD∥BC
AB = CD, AD= BC
∵四边形ABCD是
∴ ∠A=∠C, ∠B=∠D
∵ AB∥CD
∴ ∠A+∠D=1800, ∠B+∠C=1800
平行四边形的对角相等;
O
平行四边形是中心对称图形
如右图,AB=AC,且AB=5,从等腰三角形底边上任一点,分别作两腰的平行线,问:
①四边形AEDF是什么图形?为什么?
F
E
B
C
A
D
思考题
10
②图中∠1与∠B大小关系怎样?
为什么? ∠2与∠3呢?
③图中那些线段相等?为什么?
④能否求 AEDF各边长?
但能求周长吗?
1
2
3
AE=DF,ED=AF;
BE=DE,DF=CF
相等
数一数,图中有 个平行四边形。
9
可要细心哟
A
B
C
画一个平行四边形,第四个点可以在哪儿?
请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?
无数种,这些墨线都过对角线的交点
如图,在 ABCD中, ∠B=120°,DE⊥AB,垂足为E,DF⊥BC,垂足为F.求∠ADE,∠EDF,∠FDC的度数.
解:在 ABCD中,
∵∠A=∠C,AD∥BC,
∴∠A+∠B=180°.
∴∠A=180°-∠B=60°.
∴∠C=60°.
∵DE⊥AB,DF⊥BC,
∴∠ADE=∠FDC=90°-∠A=90°-60°=30°.
已知 ABCD的周长为28cm,
AB︰BC=3︰4,求它的各边的长.
解:因为在 中, AB=CD,BC=AD.所以AB+BC+CD+AD=28,即AB+BC=14.由题意得AB︰BC=3︰4,因此可设AB=3k,BC=4k,那么有3k+4k=14,解得k=2,则AB=CD=6cm,BC=AD=8cm.
ABCD
作业1. 如图,在?ABCD中,AE垂直于CD,E是垂足.如果∠B=55°,那么∠D与∠DAE分别等于多少度
解:在平行四边形ABCD中, ∠D=∠B=55°;
∵ AE垂直于CD,
∴∠AED= 90°,
∴∠DAE= 90 - ∠D= 90- 55= 35°.
作业3. 在 ABCD 中,
∠A︰∠B=2︰3,求各角的度数.
解:(1)因为∠A、∠B是平行四边形的两个邻角,所以∠A+∠B=180°.又因为∠A︰∠B=2︰3,不妨可设∠A=2k,∠B=3k,那么2k+3k=180°,可以解得k=36°,则∠A=∠C=72°,∠B=∠D=108°.
师生共勉
把一件平凡的事情做好就是不平凡
把一件简单的事情做好就是不简单
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
