第23章旋转复习课件2021—2022学年人教版数学九年级上册(28张ppt)
文档属性
| 名称 | 第23章旋转复习课件2021—2022学年人教版数学九年级上册(28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 804.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
人教版九年级数学
23章旋转(复习)
一、基础知识
知识点一:旋转
1、旋转的定义
在平面内,将一个图形绕一个 沿某个方向转动
一个 ,这样的图形运动叫做 .这个 叫做
.转动的 叫做 .
2、旋转的性质
(1)对应点到旋转中心的距离 .
(2)对应点与旋转中心所连线段的
夹角等于 .
(3)旋转前、后的图形 .
相等
旋转角
全等
点
角度
旋转
点
旋转中心
角度
旋转角
一、基础知识
知识点一
3、作旋转后的图形的一般步骤
(1)明确三个条件:
, , ;
旋转中心
旋转角
旋转方向
(2)确定关键点,作出关键点旋转
后的 ;
对应点
(3)顺次连结
一、基础知识
知识点一
练一练
1.在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有( )
A.①② B.②③ C. ①④ D.③④
A
2.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,
在这个旋转过程中:
(1)旋转中心是____旋转角是___
(2)经过旋转,点A、B分别移动到__.
O
∠AOE
E、F
一、基础知识
知识点一
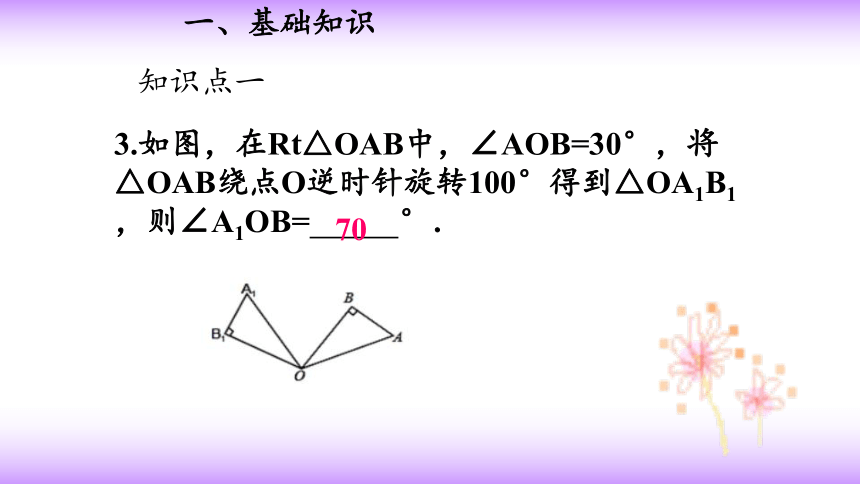
3.如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.
70
一、基础知识
知识点二: 中心对称
1、中心对称的定义
把一个图形绕着某一个点旋转_____,如果它能够与另一个图形______ ,那么就说这两个图形关于这个点______或 ______ ,这个点叫做 ______ . 这两个图形中的对应点叫做关于对称中心的______.
180°
重合
对称
中心对称
对称中心
对称点
2、中心对称的性质
(1)中心对称的两个图形,对称点所连线段都经过 ______,而且被对称中心______.
(2)中心对称的两个图形是______.
对称中心
平分
全等图形
知识点二
练一练
1.关于中心对称的两个图形,对应线段的关系是( ).
A.平行 B. 相等 C. 平行且相等
D .相等且平行或在同一直线上
2. ΔABC和ΔA’B’C’关于点O中心对称,若ΔABC的周长为12cm,ΔA’B’C’的面积为6cm2,则ΔA’B’C’的周长为______,ΔABC的面积为________。
D
12cm
6cm2
一、基础知识
知识点三:中心对称图形
1、中心对称图形的定义
把一个图形绕着某一个点旋转 ,如果旋转后的图形能够与原来的图形 ,那么这个图形叫做 ,这个点就是它的 .
180°
重合
中心对称图形
对称中心
2、中心对称图形的识别:
3、常见的几何图形,如:
线段、平行四边形、矩形、正方形、圆形等
图形旋转180 °后是否能够与原图形重合。
一、基础知识
知识点三: 练一练
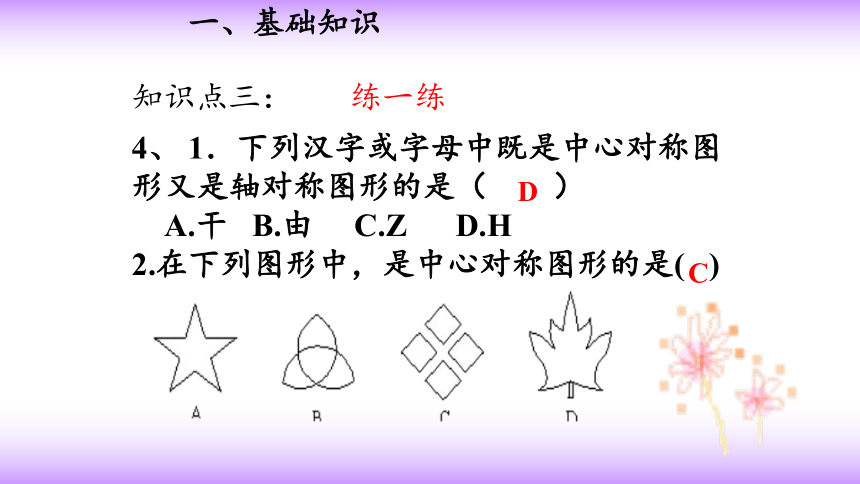
4、 1.下列汉字或字母中既是中心对称图形又是轴对称图形的是( )
A.干 B.由 C.Z D.H
2.在下列图形中,是中心对称图形的是( )
D
C
一、基础知识
知识点四 关于原点对称的点的坐标
1、关于原点对称的点的坐标特征:
点P(x,y)关于原点的对称点为
P' .
2、作关于原点成中心 对称的图形步骤:
(-x,-y)
(1)写出各点关于原点 的点的坐标;
(2)在坐标平面内描出这些 的位置;
(3)顺次 各点即为所求作的对称图形.
对称
对称点
连接
一、基础知识
一、基础知识
知识点四
练一练
1.在平面直角坐标系中,点A(-2,1)与点B关于原点对称,则点B的坐标为( )
A.(-2,1) B.(2,-1)
C.(2,1) D.(-2,-1)
B
二、强化训练
1.等边ΔABC绕绕 着它的中心,至少旋转( )度才能与它本身重合
A.60° B.120° C.180° D.360°
B
.
A.
B.
C.
2.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )
D.
A
二、强化训练
3.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形
C.菱形 D.平行四边形
4.点A(﹣3,m)和点B(n,2)关于原点对称,则m+n= .
D
1
二、强化训练
(2)画出△ABC绕点O顺时针旋转90°的△A1B1C1
A1
B1
C1
温馨提示:
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段夹角等于旋转角;
(3)旋转前、后的图形是全等图形.
二、强化训练
6.每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,
画出△ABC关于原点O
对称的△A1B1C1,
并写出A1、B1、C1.
如图,将Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠BB′C′= 度.
如图①,在△AOB 中,∠AOB=90°,OA=3,OB
=4.将△AOB沿 x 轴依次以点 A,B,O 为旋转中心顺时针旋转,
分别得到图②,图③,…,则旋转得到的图⑩的直角顶点的坐
标为________.
(36,0)
如图,△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为________
从一副扑克牌中抽出如下四张牌,其中是中心对称图形的有( )
A.1张 B.2张 C.3张 D.4张
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为________,∠APB=________°.
如图,在等腰三角形ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC= ,将△APB绕点A逆时针旋转后与△AQC重合.求:
(1)线段PQ的长;
(2)∠APC的度数.
如图,在△ABC中,∠CAB=90°,AB=AC,M、N
为BC上的两点,且∠MAN=45°,MN2与NC2+BM2有何关系?请证明你的结论.
组织交流·释疑拓展
1、如图,在正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交BC,DC于点M,N,线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
操作探究
猜想:BM+DN=MN
证明:延长CB至点N',使________,连接AN'
∵四边形ABCD是正方形
∴AB=AD,∠ABC=∠D=90°∴∠ABN'=90°
在△ABN'和△ADN中,
∴△ABN'≌△ADN(______),
∴AN'=AN,∠1=∠____,
∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=____°,∴∠1+∠3=____°,
∴∠N'AM=∠NAM,
在△AN'M和△ANM中,
∴△AN'M≌△ANM(____),
∴MN'=MN,
又MN'=BN'+BM=DN+BM,
∴BM+DN=MN
如图,正方形ABCD中,∠MAN=45°,
∠MAN的两边分别交BD于点M,N.
延长CD至点M',使DM'=BM,连接AM',
下列结论:
①AM=AM' ②∠NAM'=∠NAM
③ BM+DN=MN ④AN=AM,
其中正确的是:
A. ①② B.②④ C.①②③ D.①④
组织交流·释疑拓展
变式教学·检测反馈
2、如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
1
如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A逆时针旋转到如图的位置时,它的两边分别交BC,CD的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
2
变式教学·检测反馈
教科书第60页第3、6题
布置作业
再见
人教版九年级数学
23章旋转(复习)
一、基础知识
知识点一:旋转
1、旋转的定义
在平面内,将一个图形绕一个 沿某个方向转动
一个 ,这样的图形运动叫做 .这个 叫做
.转动的 叫做 .
2、旋转的性质
(1)对应点到旋转中心的距离 .
(2)对应点与旋转中心所连线段的
夹角等于 .
(3)旋转前、后的图形 .
相等
旋转角
全等
点
角度
旋转
点
旋转中心
角度
旋转角
一、基础知识
知识点一
3、作旋转后的图形的一般步骤
(1)明确三个条件:
, , ;
旋转中心
旋转角
旋转方向
(2)确定关键点,作出关键点旋转
后的 ;
对应点
(3)顺次连结
一、基础知识
知识点一
练一练
1.在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有( )
A.①② B.②③ C. ①④ D.③④
A
2.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,
在这个旋转过程中:
(1)旋转中心是____旋转角是___
(2)经过旋转,点A、B分别移动到__.
O
∠AOE
E、F
一、基础知识
知识点一
3.如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.
70
一、基础知识
知识点二: 中心对称
1、中心对称的定义
把一个图形绕着某一个点旋转_____,如果它能够与另一个图形______ ,那么就说这两个图形关于这个点______或 ______ ,这个点叫做 ______ . 这两个图形中的对应点叫做关于对称中心的______.
180°
重合
对称
中心对称
对称中心
对称点
2、中心对称的性质
(1)中心对称的两个图形,对称点所连线段都经过 ______,而且被对称中心______.
(2)中心对称的两个图形是______.
对称中心
平分
全等图形
知识点二
练一练
1.关于中心对称的两个图形,对应线段的关系是( ).
A.平行 B. 相等 C. 平行且相等
D .相等且平行或在同一直线上
2. ΔABC和ΔA’B’C’关于点O中心对称,若ΔABC的周长为12cm,ΔA’B’C’的面积为6cm2,则ΔA’B’C’的周长为______,ΔABC的面积为________。
D
12cm
6cm2
一、基础知识
知识点三:中心对称图形
1、中心对称图形的定义
把一个图形绕着某一个点旋转 ,如果旋转后的图形能够与原来的图形 ,那么这个图形叫做 ,这个点就是它的 .
180°
重合
中心对称图形
对称中心
2、中心对称图形的识别:
3、常见的几何图形,如:
线段、平行四边形、矩形、正方形、圆形等
图形旋转180 °后是否能够与原图形重合。
一、基础知识
知识点三: 练一练
4、 1.下列汉字或字母中既是中心对称图形又是轴对称图形的是( )
A.干 B.由 C.Z D.H
2.在下列图形中,是中心对称图形的是( )
D
C
一、基础知识
知识点四 关于原点对称的点的坐标
1、关于原点对称的点的坐标特征:
点P(x,y)关于原点的对称点为
P' .
2、作关于原点成中心 对称的图形步骤:
(-x,-y)
(1)写出各点关于原点 的点的坐标;
(2)在坐标平面内描出这些 的位置;
(3)顺次 各点即为所求作的对称图形.
对称
对称点
连接
一、基础知识
一、基础知识
知识点四
练一练
1.在平面直角坐标系中,点A(-2,1)与点B关于原点对称,则点B的坐标为( )
A.(-2,1) B.(2,-1)
C.(2,1) D.(-2,-1)
B
二、强化训练
1.等边ΔABC绕绕 着它的中心,至少旋转( )度才能与它本身重合
A.60° B.120° C.180° D.360°
B
.
A.
B.
C.
2.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )
D.
A
二、强化训练
3.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形
C.菱形 D.平行四边形
4.点A(﹣3,m)和点B(n,2)关于原点对称,则m+n= .
D
1
二、强化训练
(2)画出△ABC绕点O顺时针旋转90°的△A1B1C1
A1
B1
C1
温馨提示:
(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段夹角等于旋转角;
(3)旋转前、后的图形是全等图形.
二、强化训练
6.每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,
画出△ABC关于原点O
对称的△A1B1C1,
并写出A1、B1、C1.
如图,将Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠BB′C′= 度.
如图①,在△AOB 中,∠AOB=90°,OA=3,OB
=4.将△AOB沿 x 轴依次以点 A,B,O 为旋转中心顺时针旋转,
分别得到图②,图③,…,则旋转得到的图⑩的直角顶点的坐
标为________.
(36,0)
如图,△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为________
从一副扑克牌中抽出如下四张牌,其中是中心对称图形的有( )
A.1张 B.2张 C.3张 D.4张
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离为________,∠APB=________°.
如图,在等腰三角形ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC= ,将△APB绕点A逆时针旋转后与△AQC重合.求:
(1)线段PQ的长;
(2)∠APC的度数.
如图,在△ABC中,∠CAB=90°,AB=AC,M、N
为BC上的两点,且∠MAN=45°,MN2与NC2+BM2有何关系?请证明你的结论.
组织交流·释疑拓展
1、如图,在正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交BC,DC于点M,N,线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
操作探究
猜想:BM+DN=MN
证明:延长CB至点N',使________,连接AN'
∵四边形ABCD是正方形
∴AB=AD,∠ABC=∠D=90°∴∠ABN'=90°
在△ABN'和△ADN中,
∴△ABN'≌△ADN(______),
∴AN'=AN,∠1=∠____,
∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=____°,∴∠1+∠3=____°,
∴∠N'AM=∠NAM,
在△AN'M和△ANM中,
∴△AN'M≌△ANM(____),
∴MN'=MN,
又MN'=BN'+BM=DN+BM,
∴BM+DN=MN
如图,正方形ABCD中,∠MAN=45°,
∠MAN的两边分别交BD于点M,N.
延长CD至点M',使DM'=BM,连接AM',
下列结论:
①AM=AM' ②∠NAM'=∠NAM
③ BM+DN=MN ④AN=AM,
其中正确的是:
A. ①② B.②④ C.①②③ D.①④
组织交流·释疑拓展
变式教学·检测反馈
2、如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
1
如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A逆时针旋转到如图的位置时,它的两边分别交BC,CD的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
2
变式教学·检测反馈
教科书第60页第3、6题
布置作业
再见
同课章节目录
