第26章第3课时反比例函数k的几何意义课件2021-2022学年人教版数学九年级下册(17张ppt)
文档属性
| 名称 | 第26章第3课时反比例函数k的几何意义课件2021-2022学年人教版数学九年级下册(17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 670.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 21:58:27 | ||
图片预览




文档简介
(共17张PPT)
第二十六章 反比例函数
与反比例函数有关的面积问题
k 的几何意义及应用
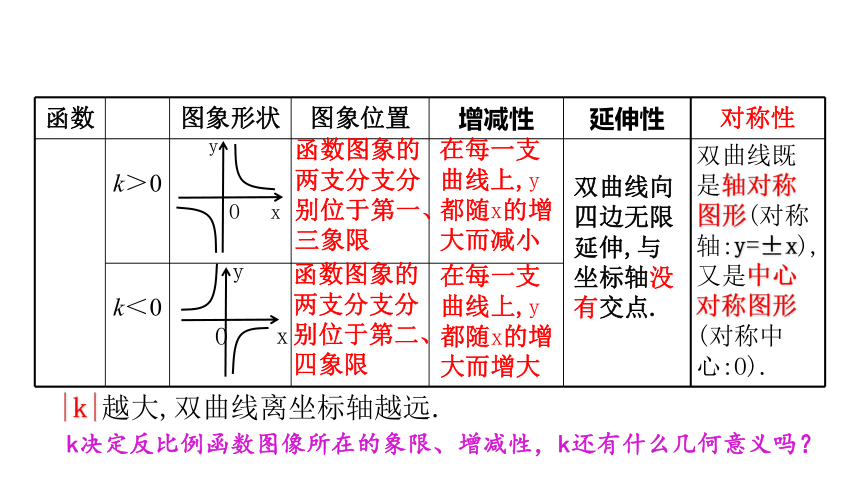
函数 图象形状 图象位置 增减性 延伸性 对称性
k>0
k<0
双曲线既是轴对称图形(对称轴:y=±x),又是中心对称图形(对称中心:O).
|k|越大,双曲线离坐标轴越远.
函数图象的两支分支分别位于第一、三象限
函数图象的两支分支分别位于第二、四象限
在每一支曲线上,y都随x的增大而减小
在每一支曲线上,y都随x的增大而增大
双曲线向四边无限延伸,与坐标轴没有交点.
y
O
x
y
O
x
k决定反比例函数图像所在的象限、增减性,k还有什么几何意义吗?
P( 3 , 2)
A
o
y
x
B
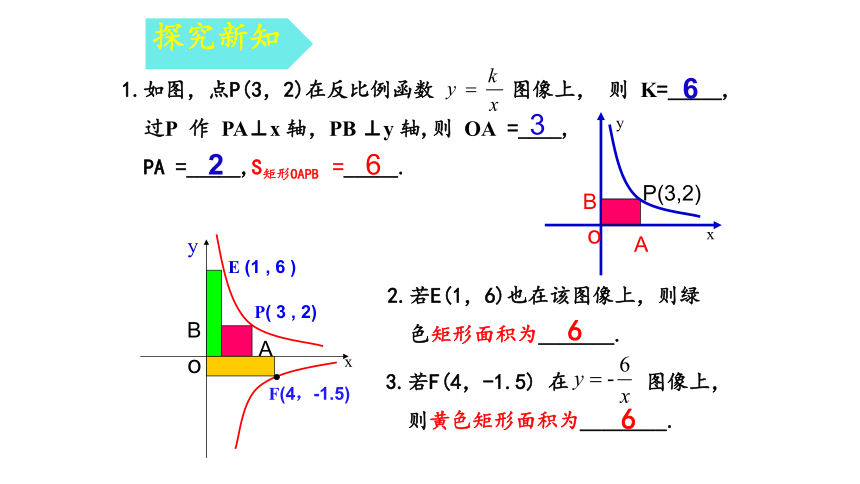
2.若E(1,6)也在该图像上,则绿
色矩形面积为_______.
E (1 , 6 )
F(4,-1.5)
3.若F(4,-1.5) 在 图像上,
则黄色矩形面积为________.
1.如图,点P(3,2)在反比例函数 图像上, 则 K=_____,
过P 作 PA⊥x 轴,PB ⊥y 轴,则 OA =____,
PA =_____,S矩形OAPB =_____.
6
P(3,2)
A
o
y
x
B
3
2
6
6
6
探究新知
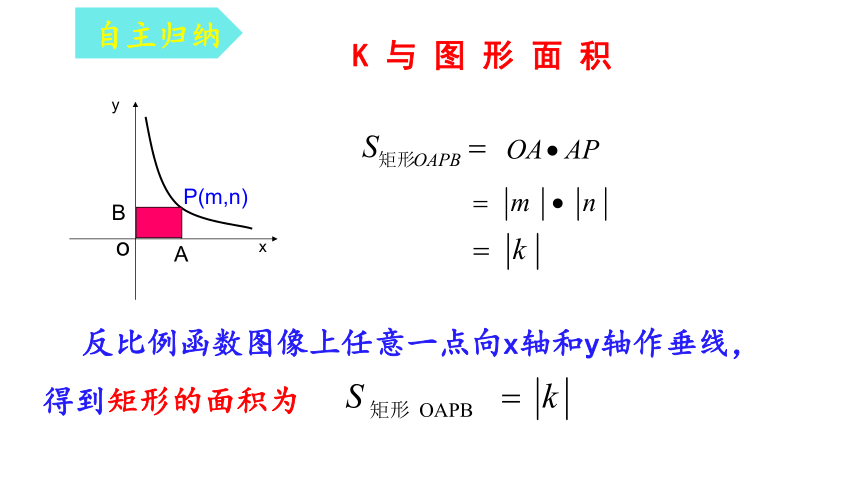
P(m,n)
A
o
y
x
B
自主归纳
K 与 图 形 面 积
反比例函数图像上任意一点向x轴和y轴作垂线,得到矩形的面积为
如图:连接OP,则
P(m,n)
A
o
y
x
B
反比例函数图像上任意一点向x轴或y轴作垂线,与原点围成三角形的面积为
S△ABC=︱K︱
SABCD=2︱K︱
B
D
S= ︱ k︱
o
y
P(m,n)
x
A
B
C
D
C
o
x
y
A
拓展变形
1.如图:在函数 的图像上有三点A、B 、C,过这三点分别向x轴、y轴作垂线,过每一点所作的两条垂线与x轴、 y轴围成的矩形的面积分别为sA , sB, sC,则( )
A . sA >sB>sC B . sAC . sA =SB=sC D. sAy
x
o
A
B
C
C
拓展练习
2.在双曲线 上任一点分别作x轴、y轴的垂线段,与x轴y轴围成矩形面积为 12,求函数解析式_______________。
或
3.已知点A是反比例函数 上的点,过点A 作AP⊥ x轴于点p,则△AOP的面积为( )
A. 12 B. 6 C. 4 D. 3
B
y
x
0
P
A
拓展练习
4.如图,A,B是双曲线 上的点,分别经过A, B两点向x轴、y轴作垂线段,若________.
4
A
o
y
x
B
S1
S2
5.若D、E、F是此反比例函数在第三象限图像上的三个点,过D、E、F分别作x轴的垂线,垂足分别为M,N、K,连接OD、OE、OF,设△ ODM、△OEN、 △OFK 的面积分别为S1、S2、S3,则下列结论成立的是( )
A S1﹤S2 ﹤ S3
B S1﹥S2 ﹥ S3
C S1 ﹤ S3 ﹤ S3
D S1 = S2 = S3
y
x
o
D
E
F
M
N
K
A(1,4)
D
拓展练习
6
D
-2
5
k1<k2<k3
(1)m= ;
(2)当x≤-2时,y的取值范围是 ;
(3)若点(a,y)在该函数图象上,且a>-2,求y的取值范围.
0<y≤3
-6
(1)求k和m的值;
(2)当x≥8时,求函数值y的取值范围.
第二十六章 反比例函数
与反比例函数有关的面积问题
k 的几何意义及应用
函数 图象形状 图象位置 增减性 延伸性 对称性
k>0
k<0
双曲线既是轴对称图形(对称轴:y=±x),又是中心对称图形(对称中心:O).
|k|越大,双曲线离坐标轴越远.
函数图象的两支分支分别位于第一、三象限
函数图象的两支分支分别位于第二、四象限
在每一支曲线上,y都随x的增大而减小
在每一支曲线上,y都随x的增大而增大
双曲线向四边无限延伸,与坐标轴没有交点.
y
O
x
y
O
x
k决定反比例函数图像所在的象限、增减性,k还有什么几何意义吗?
P( 3 , 2)
A
o
y
x
B
2.若E(1,6)也在该图像上,则绿
色矩形面积为_______.
E (1 , 6 )
F(4,-1.5)
3.若F(4,-1.5) 在 图像上,
则黄色矩形面积为________.
1.如图,点P(3,2)在反比例函数 图像上, 则 K=_____,
过P 作 PA⊥x 轴,PB ⊥y 轴,则 OA =____,
PA =_____,S矩形OAPB =_____.
6
P(3,2)
A
o
y
x
B
3
2
6
6
6
探究新知
P(m,n)
A
o
y
x
B
自主归纳
K 与 图 形 面 积
反比例函数图像上任意一点向x轴和y轴作垂线,得到矩形的面积为
如图:连接OP,则
P(m,n)
A
o
y
x
B
反比例函数图像上任意一点向x轴或y轴作垂线,与原点围成三角形的面积为
S△ABC=︱K︱
SABCD=2︱K︱
B
D
S= ︱ k︱
o
y
P(m,n)
x
A
B
C
D
C
o
x
y
A
拓展变形
1.如图:在函数 的图像上有三点A、B 、C,过这三点分别向x轴、y轴作垂线,过每一点所作的两条垂线与x轴、 y轴围成的矩形的面积分别为sA , sB, sC,则( )
A . sA >sB>sC B . sA
x
o
A
B
C
C
拓展练习
2.在双曲线 上任一点分别作x轴、y轴的垂线段,与x轴y轴围成矩形面积为 12,求函数解析式_______________。
或
3.已知点A是反比例函数 上的点,过点A 作AP⊥ x轴于点p,则△AOP的面积为( )
A. 12 B. 6 C. 4 D. 3
B
y
x
0
P
A
拓展练习
4.如图,A,B是双曲线 上的点,分别经过A, B两点向x轴、y轴作垂线段,若________.
4
A
o
y
x
B
S1
S2
5.若D、E、F是此反比例函数在第三象限图像上的三个点,过D、E、F分别作x轴的垂线,垂足分别为M,N、K,连接OD、OE、OF,设△ ODM、△OEN、 △OFK 的面积分别为S1、S2、S3,则下列结论成立的是( )
A S1﹤S2 ﹤ S3
B S1﹥S2 ﹥ S3
C S1 ﹤ S3 ﹤ S3
D S1 = S2 = S3
y
x
o
D
E
F
M
N
K
A(1,4)
D
拓展练习
6
D
-2
5
k1<k2<k3
(1)m= ;
(2)当x≤-2时,y的取值范围是 ;
(3)若点(a,y)在该函数图象上,且a>-2,求y的取值范围.
0<y≤3
-6
(1)求k和m的值;
(2)当x≥8时,求函数值y的取值范围.
