人教版七年级下册第五章相交线与平行线典型例题(74张ppt)
文档属性
| 名称 | 人教版七年级下册第五章相交线与平行线典型例题(74张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 22:03:22 | ||
图片预览








文档简介
(共74张PPT)
相交线与平行线典型例题
如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
a
b
)
(
1
3
4
2
)
(
变式1:若∠1= 32°20′,求∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
一.利用对顶角、领补角的性质求角的度数
解:设∠1=x°,则∠2=3x°,
变式3:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180,
所以 x=45,
根据对顶角相等,可得∠3=∠1=45°.
则∠1=45°,
变式2:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
(3)若 1: 2 = 2: 7 ,则∠1,∠2,∠3,∠4的度数分别为________________________.
(2)若∠2是∠3的 3倍,则∠1,∠2,∠3,∠4的度数分别为________________________.
(1)若∠1+∠3= 60 ,则∠1,∠2,∠3,∠4的度数分别为________________________ .
30 、150 、30 、150
45 、 135 、 45 、 135
40 、140 、40 、140
如图所示,直线a和b相交于点O,完成下列各题:
如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:∵∠1=40°, ∠BOC=110°(已知),
∴∠BOF=∠BOC-∠1 =110°-40°=70°.
∵∠BOF=∠2(对顶角相等),
∴∠2=70°(等量代换).
提示:隐含条件“对顶角相等”.
二.利用隐含条件求角的度数
如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ EF与AB相交,∠1+∠2=180°,
∠2+∠3= 180°,
∴∠2的补角有∠1和∠3;
∵ CD与MN相交,∠5+∠8=180°,
∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8;
∴∠2的补角有∠1、∠3、∠6和∠8.
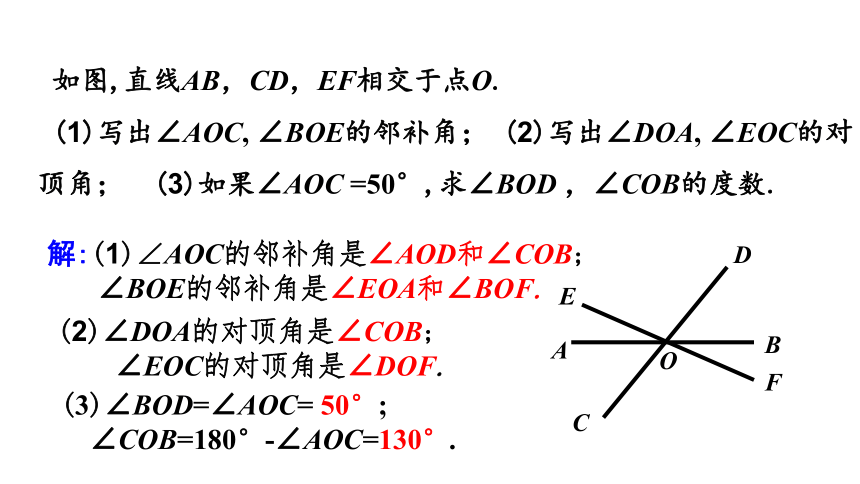
如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
C
A
E
D
B
F
O
解:(1)∠AOC的邻补角是∠AOD和∠COB;
∠BOE的邻补角是∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB;
∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°;
∠COB=180°-∠AOC=130°.
如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数.
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
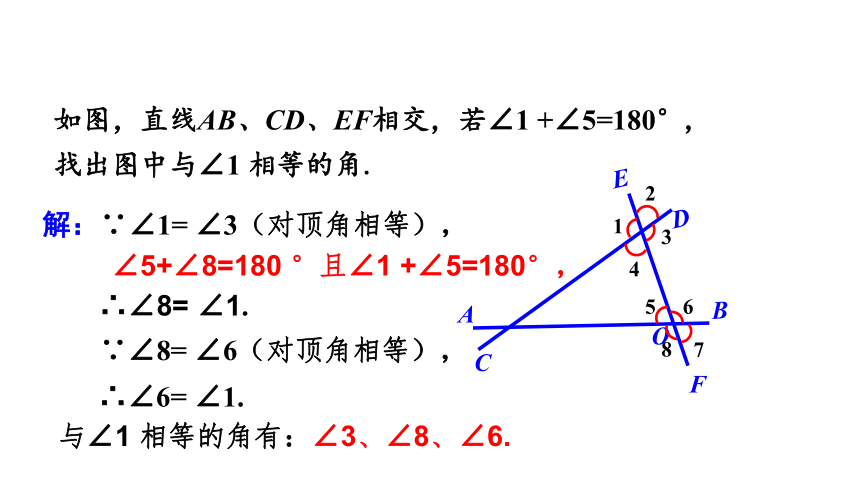
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,
找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵∠1= ∠3(对顶角相等),
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°,
∴∠8= ∠1.
∵∠8= ∠6(对顶角相等),
∴∠6= ∠1.
与∠1 相等的角有:∠3、∠8、∠6.
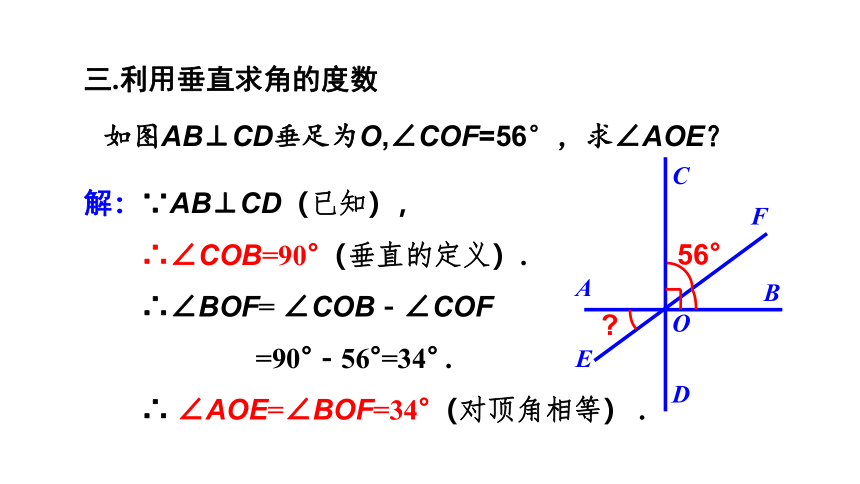
如图AB⊥CD垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等) .
F
E
D
C
B
A
O
56°
三.利用垂直求角的度数
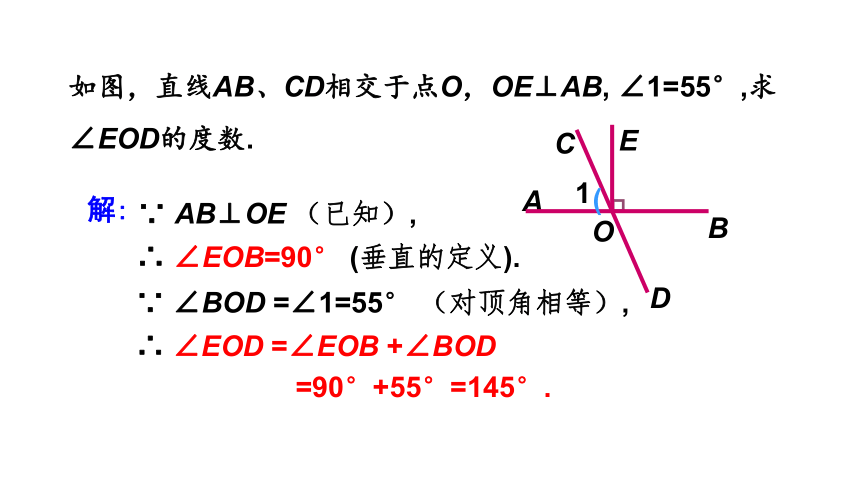
如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义).
∴ ∠EOD =∠EOB +∠BOD
=90°+55°=145°.
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知),
∵ ∠BOD =∠1=55° (对顶角相等),
解:
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON =180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
0cm
20cm
30cm
10cm
如图,(1)画出线段BC的中点M,连结AM;
(2)比较点B与点C到直线AM的距离.
A
B
C
M
P
Q
0cm
20cm
30cm
10cm
0cm
20cm
30cm
10cm
9cm
9cm
∴BP=CQ
四.画出点到直线的距离
C
A
B
0m
20m
30m
10m
0m
20m
30m
10m
8m
25m
如图,量出
(1)村庄A与货场B的距离,
(2)货场B到铁道的距离.
五.测量点线间距离
马路两旁两名同学A、B,若A同学到马路对边怎样走最近?若A同学到B同学处怎样走最近?
解:过点A作AC⊥BC,垂足为C,A同学沿着AC走到路对面最近,根据
A
B
C
连接AB, A同学沿着AB走到B同学处最近,根据
垂线段最短.
两点之间线段最短.
如图三角形ABC,根据要求画图:
要求:过点B画出点B到AC的垂线段BF.
解:如图所示:
A
C
B
F
如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小.
解:∵ AC⊥BC于C (已知),
∴ AC<AB(垂线的性质二) .
又∵ CD⊥AD于D(已知),
∴ CD<AC(垂线的性质二).
∵ DE⊥CE于E(已知),
∴ DE<CD(垂线的性质二).
∴ AB>AC>CD>DE.
如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3,∠1和∠4各是什么位置关系的角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角.
提示:解题之前要明确哪两条直线被哪条直线所截.
六.各类角的综合题
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么 ∠1=∠2.
4
3
2
1
F
E
D
C
B
A
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠1+∠3=180°,即∠1与∠3互补.
a
7
8
5
3
2
6
4
1
c
b
找出图中的同位角、内错角 、同旁内角:
4
3
2
1
6
5
7
8
c
b
a
解:同位角:∠1与∠8,∠2与∠5,∠3与∠6,∠4与∠7;
内错角: ∠1与∠6,∠4与∠5;
同旁内角:∠1与∠5 ,∠4与∠6.
3
2
4
1
c
b
a
找出图中的同位角、内错角、同旁内角:
解:同位角:
∠1与∠3,∠2与∠4;
同旁内角:∠2与∠3.
如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,
E
D
C
B
A
8
7
6
5
4
3
2
1
七.在复杂图形中识别同位角、内错角、同旁内角
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6与∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
识别这些角是同位角、内错角还是同旁内角.
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
∠A与∠8是哪两条直线被哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
下列说法中,正确的是( )
(1)过一点,有且只有一条直线与已知直线平行;
(2)平行于同一条直线的两条直线互相平行;
(3)一条直线的平行线有且只有一条;
(4)若a∥b,b∥c,则a∥c.
A.(1)(2) B.(2)(3)
C.(1)(3) D.(2)(4)
八.平行公理及其推论的应用
D
×
√
×
√
如图所示,AD∥BC,P是AB的中点.
(1)画出线段PQ,使PQ∥AD,PQ与DC交于Q点;
(2)PQ与BC平行吗 为什么?
(3)测量DQ、CQ,判断DQ和CQ是否相等 测量AD、BC、PQ,判断AD+BC=2PQ是否成立?
答:(1)线段PQ如图所示;
(2)PQ与BC平行,理由如下:
因为 AD∥BC,PQ∥AD,所以PQ∥BC(如果两条直线都与第三条直线平行,那么这两条直线也互相平行);
(3)经测量DQ=CQ,AD+BC=2PQ成立.
如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
a
b
c
d
解: a ∥d ,理由如下:
因为 a ∥b,b∥c,所以 a ∥c
( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,所以 a ∥d
( )
下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程.
解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3
∴ AB∥CD
B
1
A
C
D
F
3
7
E
( ),
已知
( ),
对顶角相等
( )
等量代换 .
( )
同位角相等,两直线平行 .
九.利用同位角相等判定两直线平行
已知∠3=45 °,∠1与∠2互余,试说明AB//CD ?
解:∵∠1=∠2(对顶角相等),
∠1与∠2互余,
∴ ∠1+∠2=90°(已知).
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
如图,如果 1+ 2=180° ,你能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知),
1+ 3=180°(邻补角的性质),
∴ 2= 3(同角的补角相等) .
∴a//b(同位角相等,两直线平行) .
2
b
a
1
3
十.利用同旁内角互补判定两直线平行
如图:直线AB、CD都和AE相交,且∠1+∠A=180 .求证:AB//CD .
证明:∵∠1+∠A=180
C
B
A
D
2
1
E
3
∴∠2+∠A=180
( ).
( ),
已知
对顶角相等
等量代换
( ).
同旁内角互补,两直线平行
∠1=∠2 ( ),
∴
AB∥CD
十一.利用同旁内角互补判定两直线平行
理由如下:
∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知) ,
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
∴ AB∥MN(内错角相等,两直线平行).
∵ ∠MCA= ∠ A(已知),
又 ∵∠ DEC= ∠ B(已知),
∴ AB∥DE(同位角相等,两直线平行).
∴ DE∥MN(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
解:
DE∥MN.
如图,为了说明示意图中的平安大街与长安街是互相平行的,在地图上量得∠1=90°,你能通过度量图中已标出的其他的角来验证这个结论吗?说出你的理由.
解:方法1:测出∠3=90°,理由是同位角相等,
两直线平行.
方法2:测出∠2=90°,理由是同旁内角互补,两
直线平行.
方法3:测出∠5=90°,理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
十二.平行线判定方法的应用
∵ ∠1=∠C (已知),
∴ MN∥BC (内错角相等,两直线平行).
∵ ∠2=∠B (已知),
∴ EF∥BC (同位角相等,两直线平行).
∴ MN∥EF ( ).
证明:
F
E
M
N
A
2
1
B
C
已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
平行于同一直线的两条直线平行
如图所示,已知BE、EC分别平分∠ABC,∠BCD,且∠1与∠2互余,试说明AB∥DC.
解:∵∠1与∠2互余,∴∠1+∠2=90°.
∵BE,EC分别平分∠ABC,∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∴∠ABC+∠BCD
=2∠1+2∠2=2(∠1+∠2)
=180°.
∴AB∥DC.
如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解: AB∥CD,
过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
∵AB∥FQ.
∴∠1+∠NFQ=180°,
∴CD∥FQ,
Q
理由如下:
∴AB∥CD.
又∵∠1=140°,
如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,
∠AED=40°.(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE∥BC,
∵∠ADE=60°,∠B=60°,∴∠ADE= ∠B.
∴DE∥BC ( ).
同位角相等,两直线平行
(2) ∠C =40°.
( )
∵∠AED=40°,∴∠C =40°.
两直线平行,同位角相等
十三.利用“两直线平行,同位角相等”求角的度数
∵DE∥BC ,∴∠C = ∠AED.
A
B
C
D
E
如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
a
b
c
1
2
∴∠ 2= 50° (等量代换).
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
十四.利用“两直线平行,内错角相等”求角的度数
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:∵梯形上、下底互相平行,
∴ ∠A与∠D互补, ∠B与∠C互补.
∴梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
十五.利用“两直线平行,同旁内角互补”求角的度数
解: ∵ AB∥DE( ),
∴∠A= ______ ( ).
∵AC∥DF( ),
∴∠D+ _______=180o ( ).
∴∠A+∠D=180o( ).
有这样一道题:如图,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3.
∵两直线平行,内错角相等,
∴∠2=∠3.
∴∠1=∠2=∠3=∠4.
∴进入潜望镜的光线和离开潜望镜
的光线平行.
∵∠1=∠2,∠3=∠4,
∴ ∠5=∠6.
证明:∵ AD ∥BC(已知),
∴ ∠A+∠B=180°( ).
∵ ∠AEF=∠B(已知),
∴ ∠A+∠AEF=180°(等量代换).
∴ AD∥EF( ).
【思考】在填写依据时要注意什么问题?
两直线平行,同旁内角互补
同旁内角互补,两直线平行
十六.平行线性质和判定的综合应用
如图,已知:AD∥BC, ∠AEF=∠B,
求证:AD∥EF.
如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB.
F
十七.添加辅助线的证明题
∴EF//CD.
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系.
解:过点E作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
B
D
C
E
A
【讨论1】如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
…
A
B
C
D
E1
E2
En
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C
= 180°
(n+1)
若有n个拐点,你能找到规律吗?
【讨论2】如图,若AB∥CD, 则:
A
B
C
D
E
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时: ∠A+∠ F1 +∠C
= ∠ E1 +∠ E2
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
∠A+∠F1 + ∠ F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+∠Em-1+ ∠D
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角,你能找到规律吗?
如图所示,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数.
解:∵AD∥EF,∴∠2=∠DAC.
∵∠1=∠2,∴∠1=∠DAC.
∴GD∥AC.
∵∠BAC=80°,∠B=∠C,
∴2∠C=180°-∠BAC=100°.
∴∠C=50°.
∴∠BDG=50°.
∴∠BDG=∠C.
已知AB⊥BF,CD⊥BF,∠1= ∠2,
试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
∵∠1=∠2
∴AB∥EF
(内错角相等,两直线平行).
(已知),
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
解:
如图,EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.
∵EF∥AD
(已知),
∴∠2=∠3
又∵∠1=∠2
∴∠1=∠3
∴DG∥AB
∴∠BAC+∠AGD=180°
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等).
(已知),
(等量代换) .
(内错角相等,两直线平行).
(两直线平行,同旁内角互补).
D
A
G
C
B
E
F
1
3
2
解:
如图,AB∥CD,猜想∠A、∠P 、∠PCD的数量关系,并说明理由.
A
B
C
D
P
E
解法一:作∠PCE =∠APC,交AB于E.
∴ AP∥CE
∴ ∠A+∠P=∠PCE+∠AEC,
∵AB∥CD ∴ ∠ECD=∠AEC,
∴∠A+∠P =∠PCE+∠ECD=∠PCD.
∴ ∠AEC=∠A,∠P=∠PCE.
如图,AB∥CD,猜想∠BAP、∠APC 、∠PCD的数量关系,并说明理由.
A
B
C
D
P
E
解法二:作∠APE =∠BAP.
∴ EP∥AB,
∴ EP∥CD,∴∠EPC=∠PCD.
∴ ∠APE+∠APC= ∠PCD.
即∠BAP+∠APC =∠PCD.
∵AB∥CD.
判断下列四个语句中,哪个是命题, 哪个不是命题?并
说明理由:
(1)对顶角相等吗?
(2)画一条线段AB=2cm;
(3)两条直线平行,同位角相等;
(4)相等的两个角,一定是对顶角.
解:(3)(4)是命题,(1)(2)不是命题.
理由如下:(1)是问句,故不是命题;
(2)是做一件事情,也不是命题.
十八.命题的识别
分别把下列命题写成“如果……那么……”的形式.
(1)两点确定一条直线;
(2)等角的补角相等;
(3)内错角相等.
解:(1)如果有两个定点,那么过这两点有且只有一条直线;
(2)如果两个角分别是两个等角的补角,那么这两个角相等;
(3)如果两个角是内错角,那么这两个角相等.
十九.命题表述形式的变换
请将它们改写成“如果……,那么……”的形式.
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
如果两条直线被第三条直线所截,那么同旁内角互补;
如果等式两边都加同一个数,那么结果仍是等式;
如果两个数互为相反数,那么这两个数相加得0;
如果两个角是同旁内角,那么这两个角互补;
如果两个角互为对顶角,那么这两个角相等.
下列命题哪些命题是正确的,哪些命题是错误的?
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
√
√
√
二十.真假命题的识别
×
×
下列句子哪些是命题?是命题的,指出是真命题还是假命题?
(1)猪有四只脚;
(2)内错角相等;
(3)画一条直线;
(4)四边形是正方形;
(5)你的作业做完了吗?
(6)同位角相等,两直线平行;
(7)同角的补角相等;
(8)同垂直于一直线的两直线平行;
(9)过点P画线段MN的垂线;
(10)x>2.
是
真命题
否
是
假命题
是
假命题
否
是
真命题
是
真命题
是
真命题
否
否
分析:要证明AB,CD平行,就需要同位角相等的条件,图中∠1与∠3就是同位角.我们只要找到:能说明它们相等的条件就行了.
从图中,我们可以发现:∠2与∠3是对顶角,所以∠3=∠2.这样我们就找到了∠1与∠3相等的确切条件了.
如图,∠1=∠2,试说明直线AB,CD平行.
二十一.利用证明推理解决问题
证明:
∵∠2与∠3是对顶角,
∴∠3=∠2.
又∵∠1=∠2,
∴∠1=∠3.
∴AB∥CD.
B
D
C
E
A
F
1
2
3
已知:b∥c, a⊥b .
求证:a⊥c.
证明: ∵ a ⊥b(已知),
∴ ∠1=90°(垂直的定义).
又∵ b ∥ c(已知),
∴ ∠2=∠1=90°(两直线平行,同位角相等).
∴ a ⊥ c(垂直的定义).
a
b
c
1
2
二十二.利用公理定理进行推理
填空:
已知:如图,∠1=∠2,∠3=∠4,
求证:EG∥FH.
证明:∵∠1=∠2(已知), ∠AEF=∠1 ( ),
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知),∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
(1)如图所示,若∠1=∠2,则AB∥CD,试判断该命题的真假: (填“真”或“假”).
(2)若上述命题为真命题,请说明理由,若上述命题为假命题,请你再添加一条件,使该命题成为真命题,并说明理由.
假
解:加条件:BE∥FD.
理由如下:∵BE∥FD,∴∠EBD=∠FDN(两直线平行,同位角相等).
又∵∠1=∠2,∴∠ABD=∠CDN.
∴AB∥CD(同位角相等,两直线平行).
证明:∵AB∥CD(已知),
∴∠BPQ=∠CQP(两直线平行,内错角相等).
又∵PG平分∠BPQ,QH平分∠CQP(已知),
∴∠GPQ= ∠BPQ,∠HQP= ∠CQP(角平分线的定义),
∴∠GPQ=∠HQP(等量代换),
∴PG∥HQ(内错角相等,两直线平行).
如图,已知AB∥CD,直线AB,CD被直
线MN所截,交点分别为P,Q,PG平分
∠BPQ,QH平分∠CQP, 求证:PG∥HQ.
A
B
C
D
M
N
P
Q
H
G
下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段平直的铁轨上;(5)沸水中气泡的运动.
属于平移的是_______________.
二十三.平移现象的识别
平移
旋转
平移
旋转
平移
(1)(2)(4)
提示:判断生活中的现象是否是平移,要根据平移的定义,进行判断,图形平移前后的形状和大小没有变化,只是位置发生变化.
下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )
解析:根据平移的定义与特征可知,平移后的图形的形状、大小不改变,对应线段平行(或在同一直线上)且相等,对应角相等,故选A.
二十四.图形平移变换的识别
A
AA'
AA'
C
AA'
AA'
B'
C'
如图,平移三角形ABC,使点A移动
到点A',画出平移后的三角形A'B'C'.
解:(1)连接 ,
(2)过点B作AA'的平行线, 在上截取BB'= ,
(3)过点 作 的平行线,在上截取
CC'= ,
(4)连接A'B',B'C',A'C',
所得的三角形就是平移后的
三角形.
二十五.平移作图
A
B
C
A'
1m
1m
21m
15m
A
C
D
B
图 1
如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的
面积为
多少
1m
1m
21m
15m
A
C
D
B
图 1
提示:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
二十六.利用平移求面积
1m
21m
15m
A
C
D
B
【思考】如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
提示:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
如何将平行四边形ABCD平移,使点A移动到点E,画出平移后的图形.
E
A
B
C
D
F
G
H
四边形 EFGH 就是四边形ABCD平移后的图形.
(1)如图所示,图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.
(2)若长方形的长为a,宽为b,
请分别写出三个图形中除去阴
影部分后剩余部分的面积.
(3)如图④,在宽为10m,长为40m的长方形菜地上有一条弯曲的小路,小路宽为1m,求这块菜地的面积.
解:(1)如图所示:
(2)三个图形中除去阴影部分后剩余部分的面积:
①ab-b; ②ab-b; ③ab-b;
(3)(40-1)×10=390(m2).
答:这块菜地的面积为390m2.
相交线与平行线典型例题
如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
a
b
)
(
1
3
4
2
)
(
变式1:若∠1= 32°20′,求∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
一.利用对顶角、领补角的性质求角的度数
解:设∠1=x°,则∠2=3x°,
变式3:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180,
所以 x=45,
根据对顶角相等,可得∠3=∠1=45°.
则∠1=45°,
变式2:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
(3)若 1: 2 = 2: 7 ,则∠1,∠2,∠3,∠4的度数分别为________________________.
(2)若∠2是∠3的 3倍,则∠1,∠2,∠3,∠4的度数分别为________________________.
(1)若∠1+∠3= 60 ,则∠1,∠2,∠3,∠4的度数分别为________________________ .
30 、150 、30 、150
45 、 135 、 45 、 135
40 、140 、40 、140
如图所示,直线a和b相交于点O,完成下列各题:
如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:∵∠1=40°, ∠BOC=110°(已知),
∴∠BOF=∠BOC-∠1 =110°-40°=70°.
∵∠BOF=∠2(对顶角相等),
∴∠2=70°(等量代换).
提示:隐含条件“对顶角相等”.
二.利用隐含条件求角的度数
如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ EF与AB相交,∠1+∠2=180°,
∠2+∠3= 180°,
∴∠2的补角有∠1和∠3;
∵ CD与MN相交,∠5+∠8=180°,
∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8;
∴∠2的补角有∠1、∠3、∠6和∠8.
如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
C
A
E
D
B
F
O
解:(1)∠AOC的邻补角是∠AOD和∠COB;
∠BOE的邻补角是∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB;
∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°;
∠COB=180°-∠AOC=130°.
如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数.
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,
找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵∠1= ∠3(对顶角相等),
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°,
∴∠8= ∠1.
∵∠8= ∠6(对顶角相等),
∴∠6= ∠1.
与∠1 相等的角有:∠3、∠8、∠6.
如图AB⊥CD垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知),
∴∠COB=90°(垂直的定义).
∴∠BOF= ∠COB-∠COF
=90°-56°=34° .
∴ ∠AOE=∠BOF=34°(对顶角相等) .
F
E
D
C
B
A
O
56°
三.利用垂直求角的度数
如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义).
∴ ∠EOD =∠EOB +∠BOD
=90°+55°=145°.
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知),
∵ ∠BOD =∠1=55° (对顶角相等),
解:
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON =180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
0cm
20cm
30cm
10cm
如图,(1)画出线段BC的中点M,连结AM;
(2)比较点B与点C到直线AM的距离.
A
B
C
M
P
Q
0cm
20cm
30cm
10cm
0cm
20cm
30cm
10cm
9cm
9cm
∴BP=CQ
四.画出点到直线的距离
C
A
B
0m
20m
30m
10m
0m
20m
30m
10m
8m
25m
如图,量出
(1)村庄A与货场B的距离,
(2)货场B到铁道的距离.
五.测量点线间距离
马路两旁两名同学A、B,若A同学到马路对边怎样走最近?若A同学到B同学处怎样走最近?
解:过点A作AC⊥BC,垂足为C,A同学沿着AC走到路对面最近,根据
A
B
C
连接AB, A同学沿着AB走到B同学处最近,根据
垂线段最短.
两点之间线段最短.
如图三角形ABC,根据要求画图:
要求:过点B画出点B到AC的垂线段BF.
解:如图所示:
A
C
B
F
如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小.
解:∵ AC⊥BC于C (已知),
∴ AC<AB(垂线的性质二) .
又∵ CD⊥AD于D(已知),
∴ CD<AC(垂线的性质二).
∵ DE⊥CE于E(已知),
∴ DE<CD(垂线的性质二).
∴ AB>AC>CD>DE.
如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3,∠1和∠4各是什么位置关系的角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角.
提示:解题之前要明确哪两条直线被哪条直线所截.
六.各类角的综合题
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么 ∠1=∠2.
4
3
2
1
F
E
D
C
B
A
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠1+∠3=180°,即∠1与∠3互补.
a
7
8
5
3
2
6
4
1
c
b
找出图中的同位角、内错角 、同旁内角:
4
3
2
1
6
5
7
8
c
b
a
解:同位角:∠1与∠8,∠2与∠5,∠3与∠6,∠4与∠7;
内错角: ∠1与∠6,∠4与∠5;
同旁内角:∠1与∠5 ,∠4与∠6.
3
2
4
1
c
b
a
找出图中的同位角、内错角、同旁内角:
解:同位角:
∠1与∠3,∠2与∠4;
同旁内角:∠2与∠3.
如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,
E
D
C
B
A
8
7
6
5
4
3
2
1
七.在复杂图形中识别同位角、内错角、同旁内角
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6与∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
识别这些角是同位角、内错角还是同旁内角.
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
∠A与∠8是哪两条直线被哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
下列说法中,正确的是( )
(1)过一点,有且只有一条直线与已知直线平行;
(2)平行于同一条直线的两条直线互相平行;
(3)一条直线的平行线有且只有一条;
(4)若a∥b,b∥c,则a∥c.
A.(1)(2) B.(2)(3)
C.(1)(3) D.(2)(4)
八.平行公理及其推论的应用
D
×
√
×
√
如图所示,AD∥BC,P是AB的中点.
(1)画出线段PQ,使PQ∥AD,PQ与DC交于Q点;
(2)PQ与BC平行吗 为什么?
(3)测量DQ、CQ,判断DQ和CQ是否相等 测量AD、BC、PQ,判断AD+BC=2PQ是否成立?
答:(1)线段PQ如图所示;
(2)PQ与BC平行,理由如下:
因为 AD∥BC,PQ∥AD,所以PQ∥BC(如果两条直线都与第三条直线平行,那么这两条直线也互相平行);
(3)经测量DQ=CQ,AD+BC=2PQ成立.
如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
a
b
c
d
解: a ∥d ,理由如下:
因为 a ∥b,b∥c,所以 a ∥c
( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,所以 a ∥d
( )
下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程.
解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3
∴ AB∥CD
B
1
A
C
D
F
3
7
E
( ),
已知
( ),
对顶角相等
( )
等量代换 .
( )
同位角相等,两直线平行 .
九.利用同位角相等判定两直线平行
已知∠3=45 °,∠1与∠2互余,试说明AB//CD ?
解:∵∠1=∠2(对顶角相等),
∠1与∠2互余,
∴ ∠1+∠2=90°(已知).
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
如图,如果 1+ 2=180° ,你能判定a//b吗
c
解:能,
∵ 1+ 2=180°(已知),
1+ 3=180°(邻补角的性质),
∴ 2= 3(同角的补角相等) .
∴a//b(同位角相等,两直线平行) .
2
b
a
1
3
十.利用同旁内角互补判定两直线平行
如图:直线AB、CD都和AE相交,且∠1+∠A=180 .求证:AB//CD .
证明:∵∠1+∠A=180
C
B
A
D
2
1
E
3
∴∠2+∠A=180
( ).
( ),
已知
对顶角相等
等量代换
( ).
同旁内角互补,两直线平行
∠1=∠2 ( ),
∴
AB∥CD
十一.利用同旁内角互补判定两直线平行
理由如下:
∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知) ,
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
∴ AB∥MN(内错角相等,两直线平行).
∵ ∠MCA= ∠ A(已知),
又 ∵∠ DEC= ∠ B(已知),
∴ AB∥DE(同位角相等,两直线平行).
∴ DE∥MN(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
解:
DE∥MN.
如图,为了说明示意图中的平安大街与长安街是互相平行的,在地图上量得∠1=90°,你能通过度量图中已标出的其他的角来验证这个结论吗?说出你的理由.
解:方法1:测出∠3=90°,理由是同位角相等,
两直线平行.
方法2:测出∠2=90°,理由是同旁内角互补,两
直线平行.
方法3:测出∠5=90°,理由是内错角相等,两直线平行.
方法4:测出∠2,∠3,∠4,∠5中任意一个角为90°,
理由是同一平面内,垂直于同一直线的两直线平行.
十二.平行线判定方法的应用
∵ ∠1=∠C (已知),
∴ MN∥BC (内错角相等,两直线平行).
∵ ∠2=∠B (已知),
∴ EF∥BC (同位角相等,两直线平行).
∴ MN∥EF ( ).
证明:
F
E
M
N
A
2
1
B
C
已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
平行于同一直线的两条直线平行
如图所示,已知BE、EC分别平分∠ABC,∠BCD,且∠1与∠2互余,试说明AB∥DC.
解:∵∠1与∠2互余,∴∠1+∠2=90°.
∵BE,EC分别平分∠ABC,∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∴∠ABC+∠BCD
=2∠1+2∠2=2(∠1+∠2)
=180°.
∴AB∥DC.
如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解: AB∥CD,
过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
∵AB∥FQ.
∴∠1+∠NFQ=180°,
∴CD∥FQ,
Q
理由如下:
∴AB∥CD.
又∵∠1=140°,
如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,
∠AED=40°.(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE∥BC,
∵∠ADE=60°,∠B=60°,∴∠ADE= ∠B.
∴DE∥BC ( ).
同位角相等,两直线平行
(2) ∠C =40°.
( )
∵∠AED=40°,∴∠C =40°.
两直线平行,同位角相等
十三.利用“两直线平行,同位角相等”求角的度数
∵DE∥BC ,∴∠C = ∠AED.
A
B
C
D
E
如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
a
b
c
1
2
∴∠ 2= 50° (等量代换).
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
十四.利用“两直线平行,内错角相等”求角的度数
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:∵梯形上、下底互相平行,
∴ ∠A与∠D互补, ∠B与∠C互补.
∴梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
十五.利用“两直线平行,同旁内角互补”求角的度数
解: ∵ AB∥DE( ),
∴∠A= ______ ( ).
∵AC∥DF( ),
∴∠D+ _______=180o ( ).
∴∠A+∠D=180o( ).
有这样一道题:如图,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3.
∵两直线平行,内错角相等,
∴∠2=∠3.
∴∠1=∠2=∠3=∠4.
∴进入潜望镜的光线和离开潜望镜
的光线平行.
∵∠1=∠2,∠3=∠4,
∴ ∠5=∠6.
证明:∵ AD ∥BC(已知),
∴ ∠A+∠B=180°( ).
∵ ∠AEF=∠B(已知),
∴ ∠A+∠AEF=180°(等量代换).
∴ AD∥EF( ).
【思考】在填写依据时要注意什么问题?
两直线平行,同旁内角互补
同旁内角互补,两直线平行
十六.平行线性质和判定的综合应用
如图,已知:AD∥BC, ∠AEF=∠B,
求证:AD∥EF.
如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB.
F
十七.添加辅助线的证明题
∴EF//CD.
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系.
解:过点E作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
B
D
C
E
A
【讨论1】如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
…
A
B
C
D
E1
E2
En
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C
= 180°
(n+1)
若有n个拐点,你能找到规律吗?
【讨论2】如图,若AB∥CD, 则:
A
B
C
D
E
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时: ∠A+∠ F1 +∠C
= ∠ E1 +∠ E2
C
A
B
D
E1
F1
E2
Em-1
F2
Fn-1
∠A+∠F1 + ∠ F2 +…+ ∠Fn-1= ∠E1 +∠E2 +…+∠Em-1+ ∠D
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角,你能找到规律吗?
如图所示,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数.
解:∵AD∥EF,∴∠2=∠DAC.
∵∠1=∠2,∴∠1=∠DAC.
∴GD∥AC.
∵∠BAC=80°,∠B=∠C,
∴2∠C=180°-∠BAC=100°.
∴∠C=50°.
∴∠BDG=50°.
∴∠BDG=∠C.
已知AB⊥BF,CD⊥BF,∠1= ∠2,
试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
∵∠1=∠2
∴AB∥EF
(内错角相等,两直线平行).
(已知),
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
解:
如图,EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.
∵EF∥AD
(已知),
∴∠2=∠3
又∵∠1=∠2
∴∠1=∠3
∴DG∥AB
∴∠BAC+∠AGD=180°
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等).
(已知),
(等量代换) .
(内错角相等,两直线平行).
(两直线平行,同旁内角互补).
D
A
G
C
B
E
F
1
3
2
解:
如图,AB∥CD,猜想∠A、∠P 、∠PCD的数量关系,并说明理由.
A
B
C
D
P
E
解法一:作∠PCE =∠APC,交AB于E.
∴ AP∥CE
∴ ∠A+∠P=∠PCE+∠AEC,
∵AB∥CD ∴ ∠ECD=∠AEC,
∴∠A+∠P =∠PCE+∠ECD=∠PCD.
∴ ∠AEC=∠A,∠P=∠PCE.
如图,AB∥CD,猜想∠BAP、∠APC 、∠PCD的数量关系,并说明理由.
A
B
C
D
P
E
解法二:作∠APE =∠BAP.
∴ EP∥AB,
∴ EP∥CD,∴∠EPC=∠PCD.
∴ ∠APE+∠APC= ∠PCD.
即∠BAP+∠APC =∠PCD.
∵AB∥CD.
判断下列四个语句中,哪个是命题, 哪个不是命题?并
说明理由:
(1)对顶角相等吗?
(2)画一条线段AB=2cm;
(3)两条直线平行,同位角相等;
(4)相等的两个角,一定是对顶角.
解:(3)(4)是命题,(1)(2)不是命题.
理由如下:(1)是问句,故不是命题;
(2)是做一件事情,也不是命题.
十八.命题的识别
分别把下列命题写成“如果……那么……”的形式.
(1)两点确定一条直线;
(2)等角的补角相等;
(3)内错角相等.
解:(1)如果有两个定点,那么过这两点有且只有一条直线;
(2)如果两个角分别是两个等角的补角,那么这两个角相等;
(3)如果两个角是内错角,那么这两个角相等.
十九.命题表述形式的变换
请将它们改写成“如果……,那么……”的形式.
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
如果两条直线被第三条直线所截,那么同旁内角互补;
如果等式两边都加同一个数,那么结果仍是等式;
如果两个数互为相反数,那么这两个数相加得0;
如果两个角是同旁内角,那么这两个角互补;
如果两个角互为对顶角,那么这两个角相等.
下列命题哪些命题是正确的,哪些命题是错误的?
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
√
√
√
二十.真假命题的识别
×
×
下列句子哪些是命题?是命题的,指出是真命题还是假命题?
(1)猪有四只脚;
(2)内错角相等;
(3)画一条直线;
(4)四边形是正方形;
(5)你的作业做完了吗?
(6)同位角相等,两直线平行;
(7)同角的补角相等;
(8)同垂直于一直线的两直线平行;
(9)过点P画线段MN的垂线;
(10)x>2.
是
真命题
否
是
假命题
是
假命题
否
是
真命题
是
真命题
是
真命题
否
否
分析:要证明AB,CD平行,就需要同位角相等的条件,图中∠1与∠3就是同位角.我们只要找到:能说明它们相等的条件就行了.
从图中,我们可以发现:∠2与∠3是对顶角,所以∠3=∠2.这样我们就找到了∠1与∠3相等的确切条件了.
如图,∠1=∠2,试说明直线AB,CD平行.
二十一.利用证明推理解决问题
证明:
∵∠2与∠3是对顶角,
∴∠3=∠2.
又∵∠1=∠2,
∴∠1=∠3.
∴AB∥CD.
B
D
C
E
A
F
1
2
3
已知:b∥c, a⊥b .
求证:a⊥c.
证明: ∵ a ⊥b(已知),
∴ ∠1=90°(垂直的定义).
又∵ b ∥ c(已知),
∴ ∠2=∠1=90°(两直线平行,同位角相等).
∴ a ⊥ c(垂直的定义).
a
b
c
1
2
二十二.利用公理定理进行推理
填空:
已知:如图,∠1=∠2,∠3=∠4,
求证:EG∥FH.
证明:∵∠1=∠2(已知), ∠AEF=∠1 ( ),
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知),∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
(1)如图所示,若∠1=∠2,则AB∥CD,试判断该命题的真假: (填“真”或“假”).
(2)若上述命题为真命题,请说明理由,若上述命题为假命题,请你再添加一条件,使该命题成为真命题,并说明理由.
假
解:加条件:BE∥FD.
理由如下:∵BE∥FD,∴∠EBD=∠FDN(两直线平行,同位角相等).
又∵∠1=∠2,∴∠ABD=∠CDN.
∴AB∥CD(同位角相等,两直线平行).
证明:∵AB∥CD(已知),
∴∠BPQ=∠CQP(两直线平行,内错角相等).
又∵PG平分∠BPQ,QH平分∠CQP(已知),
∴∠GPQ= ∠BPQ,∠HQP= ∠CQP(角平分线的定义),
∴∠GPQ=∠HQP(等量代换),
∴PG∥HQ(内错角相等,两直线平行).
如图,已知AB∥CD,直线AB,CD被直
线MN所截,交点分别为P,Q,PG平分
∠BPQ,QH平分∠CQP, 求证:PG∥HQ.
A
B
C
D
M
N
P
Q
H
G
下列现象:(1)水平运输带上砖块的运动;(2)高楼电梯上上下下迎接乘客;(3)健身做呼啦圈运动;(4)火车飞驰在一段平直的铁轨上;(5)沸水中气泡的运动.
属于平移的是_______________.
二十三.平移现象的识别
平移
旋转
平移
旋转
平移
(1)(2)(4)
提示:判断生活中的现象是否是平移,要根据平移的定义,进行判断,图形平移前后的形状和大小没有变化,只是位置发生变化.
下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )
解析:根据平移的定义与特征可知,平移后的图形的形状、大小不改变,对应线段平行(或在同一直线上)且相等,对应角相等,故选A.
二十四.图形平移变换的识别
A
AA'
AA'
C
AA'
AA'
B'
C'
如图,平移三角形ABC,使点A移动
到点A',画出平移后的三角形A'B'C'.
解:(1)连接 ,
(2)过点B作AA'的平行线, 在上截取BB'= ,
(3)过点 作 的平行线,在上截取
CC'= ,
(4)连接A'B',B'C',A'C',
所得的三角形就是平移后的
三角形.
二十五.平移作图
A
B
C
A'
1m
1m
21m
15m
A
C
D
B
图 1
如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的
面积为
多少
1m
1m
21m
15m
A
C
D
B
图 1
提示:两种平移方式
解:长草部分的面积=(21-1)×(15-1)=280(m2).
二十六.利用平移求面积
1m
21m
15m
A
C
D
B
【思考】如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
提示:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
如何将平行四边形ABCD平移,使点A移动到点E,画出平移后的图形.
E
A
B
C
D
F
G
H
四边形 EFGH 就是四边形ABCD平移后的图形.
(1)如图所示,图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形.
(2)若长方形的长为a,宽为b,
请分别写出三个图形中除去阴
影部分后剩余部分的面积.
(3)如图④,在宽为10m,长为40m的长方形菜地上有一条弯曲的小路,小路宽为1m,求这块菜地的面积.
解:(1)如图所示:
(2)三个图形中除去阴影部分后剩余部分的面积:
①ab-b; ②ab-b; ③ab-b;
(3)(40-1)×10=390(m2).
答:这块菜地的面积为390m2.
