人教版七年级下册第七章平面直角坐标系典型例题(25张ppt)
文档属性
| 名称 | 人教版七年级下册第七章平面直角坐标系典型例题(25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 669.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 22:08:31 | ||
图片预览





文档简介
(共25张PPT)
平面直角坐标系典型例题
A
B
C
E
F
D
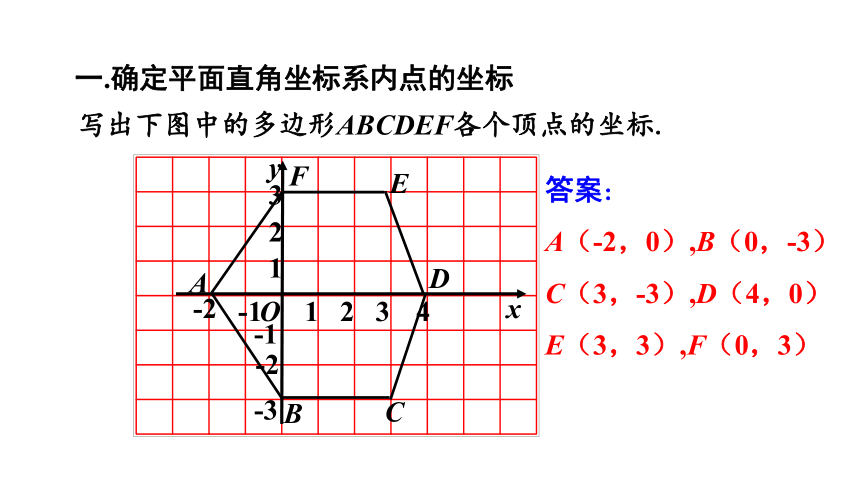
写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
y
O
x
答案:
A(-2,0),B(0,-3)
C(3,-3),D(4,0)
E(3,3),F(0,3)
一.确定平面直角坐标系内点的坐标
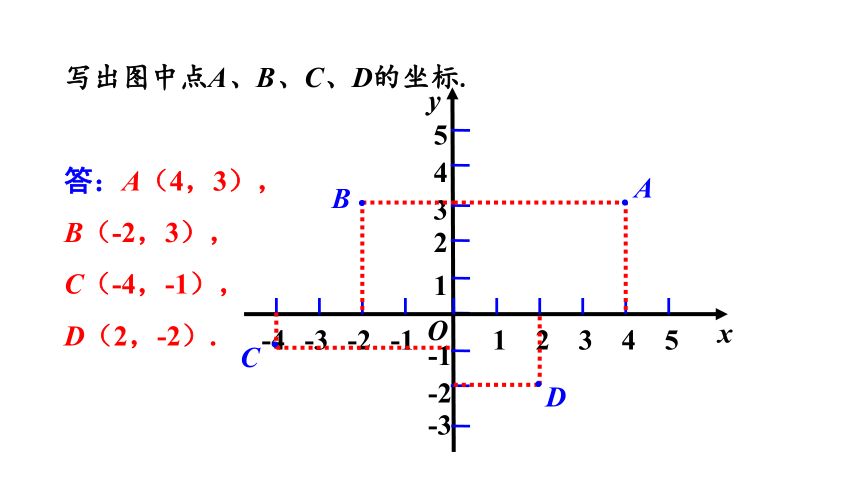
写出图中点A、B、C、D的坐标.
答:A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限. A(5,4),B(-3,4),C (-4 ,-1),D(2,-4).
二.在平面直角坐标系内确定已知点
y
5
-5
-2
-4
-1
2
3
1
-6
6
4
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
x
-3
A
(5,4)
O
B
(-3,4)
C
(-4,-1)
D
(2,-4)
解:如图,先在x 轴上找到表示5的点,再在y 轴上找出表示4 的点,过这两个点分别作x 轴,y 轴的垂线,垂线的交点就是点A. 类似地,其他各点的位置如图所示.点A 在第一象限,点B 在第二象限,点C在第三象限,点D在第四象限.
已知在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是________.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的一元一次不等式组 解得m>2.
m>2
三.利用平面直角坐标系内点的坐标确定字母的值
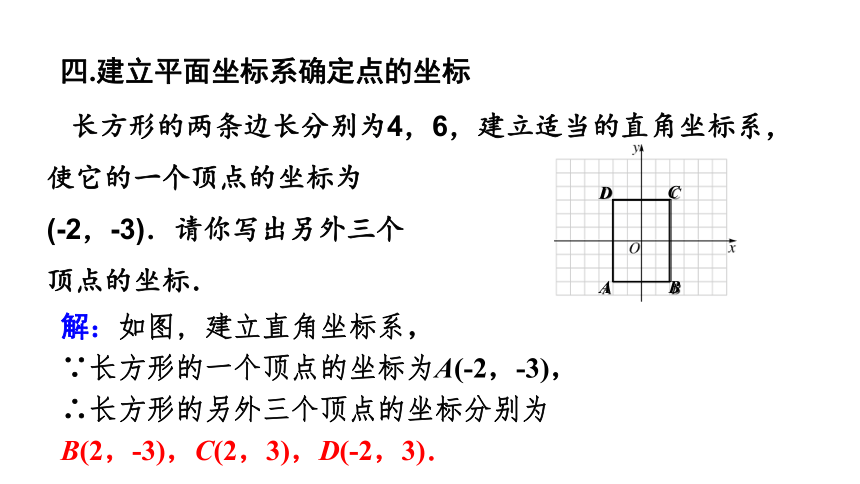
长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为
(-2,-3).请你写出另外三个
顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为
B(2,-3),C(2,3),D(-2,3).
四.建立平面坐标系确定点的坐标
A
B
C
D
O
东
北
50
50
单位:m
张明
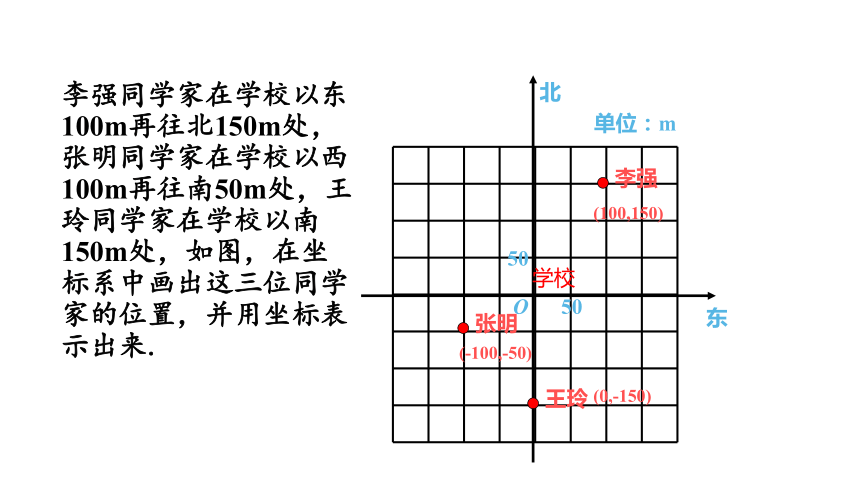
李强同学家在学校以东100m再往北150m处,张明同学家在学校以西100m再往南50m处,王玲同学家在学校以南150m处,如图,在坐标系中画出这三位同学家的位置,并用坐标表示出来.
李强
王玲
(100,150)
(-100,-50)
(0,-150)
学校
根据以下条件画一幅示意图, 标出学校、书店、电影院、汽车站的位置.
(1)从学校向东走500m,再向北走450m到书店.
(2)从学校向西走300m,再向南走300m,最后向东走50m到电影院.
(3)从学校向南走600m,再向东走400m到汽车站.
五.建立平面直角坐标系确定点的位置
解:如图,以学校所在位置为原点,分别以正东、正北方向为x 轴,y 轴的正方向,建立平面直角坐标系,规定1个单位长度代表100m长.根据题目条件,点A(5,4.5)是书店的位置,点B(-2.5,-3)是电影院的位置,点C(4,-6) 是汽车站的位置.
如图,是某次海战中敌我双方舰艇对峙示意图(图中1cm表示20 n mile),对我方潜艇O来说:
O
六.用方位角和距离表示物体位置
敌方
舰艇 C
敌方
舰艇 A
敌方舰艇 B
小岛
40
O
1cm
1cm
(1) 北偏东40°的方向上有哪些目标 要想确定敌舰B的位置,还需要什么数据
解:有敌方舰艇B和小岛;还需要敌方舰艇B与我方潜艇O的距离.
(2) 距离我方潜艇
20 n mile的敌舰有
哪几艘
解:有敌舰A和敌舰C.
解:(3)要确定每艘敌舰的位置,各需要两个数据:距离和方位角.如,对我方潜艇O来说,敌舰A在正南方向,图上距离为1cm处;
敌舰B在北偏东40°
方向,图上距离
为1.4cm处;
敌舰C在正东方向,
图上距离为1cm处.
敌方
舰艇 C
敌方
舰艇 A
敌方舰艇 B
40
O
1cm
1cm
(3) 要确定每艘敌舰的位置,各需要几个数据
1.4cm
长方形零件如图1(单位:mm),建立适当的坐标系,用坐标表示孔心的位置.如图2,货轮与灯塔相距40 n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
图1
图2
解:1、以长方形左下角的顶点为原点,长所在的直线为x轴(向右为正方向),宽所在的直线为y轴(向上为正方向)建立直角坐标系,则孔心的坐标是(15,25).
2、灯塔在货轮的南偏东500 ,40n mile处,货轮在灯塔的北偏西500 ,40n mile处.
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
提示:左减右加,下减上加.
七.平面直角坐标系内点的平移
①将点(2,1)向右平移3个单位长度,
可以得到对应点坐标__________ ;
②将点(2,-1)向左平移3个单位长度,
可以得到对应点坐标__________ ;
③将点(2,5)向上平移3个单位长度,
可以得到对应点坐标__________ ;
④将点(-2,5)向下平移3单位长度,
可以得到对应点坐标__________.
(5,1)
(-1,-1)
(2,8)
(-2,2)
根据平移填空:
如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的三角
形A1B1C1,并写出点A、C、
A1、C1的坐标;
1
y
O
1
x
A
B
C
A1
B1
C1
解:(1)三角形A1B1C1如图所示,各点的坐标分别为A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
P
P1
八.平面直角坐标系内图形的平移
C
1
y
O
1
x
A
B
C
A1
B1
C1
(2) 求出以A、C、A1、C1为顶点的四边形的面积.
解:(2)连接AA1,CC1,
P
P1
如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
A′
B′
C′
D′
解:如图所示,四边形A′B′C′D′就是所要画的四边形,
A′(-3,1), B′(1,1), C′(2,4), D′(-2,4).
在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
A.(-1,-1) B.(1,0)
C.(-1,0) D.(3,0)
A
C
如图所示,将点A向右平移( )个单位长度可得到点B .
A.3个单位长度 B. 4个单位长度 C.5个单位长度 D.6个单位长度
如图所示,将点A向下平移5个单位长度后,将重合于图中的 ( )
A.点C B.点F
C.点D D.点E
B
D
F
y
x
0
-4
-3
-2
-1
1
2
3
4
1
2
3
4
-1
-2
-3
-4
C
D
A
B
E
G
如图所示,点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G′,则G′的坐标为( )
A.(6,5) B.(4,5) C.(6,3) D.(4,3)
D
F
y
x
0
-4
-3
-2
-1
1
2
3
4
1
2
3
4
-1
-2
-3
-4
C
D
A
B
E
G
如图所示,将点A先向右平移3个单位长度,再向下平移5个单位长度,得到A′为__________;将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B′为________,则A′与B′相距____个单位长度.
(0,-3)
(4,-3)
4
F
y
x
0
-4
-3
-2
-1
1
2
3
4
1
2
3
4
-1
-2
-3
-4
C
D
A
B
E
G
已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为____________________;
已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为___________________.
(-1,-2)或(-1,6)
(3,2)或(-5,2)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3);C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
C
O
A1
C1
B1
平面直角坐标系典型例题
A
B
C
E
F
D
写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
y
O
x
答案:
A(-2,0),B(0,-3)
C(3,-3),D(4,0)
E(3,3),F(0,3)
一.确定平面直角坐标系内点的坐标
写出图中点A、B、C、D的坐标.
答:A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
在平面直角坐标系中,描出下列各点,并指出它们分别在哪个象限. A(5,4),B(-3,4),C (-4 ,-1),D(2,-4).
二.在平面直角坐标系内确定已知点
y
5
-5
-2
-4
-1
2
3
1
-6
6
4
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
x
-3
A
(5,4)
O
B
(-3,4)
C
(-4,-1)
D
(2,-4)
解:如图,先在x 轴上找到表示5的点,再在y 轴上找出表示4 的点,过这两个点分别作x 轴,y 轴的垂线,垂线的交点就是点A. 类似地,其他各点的位置如图所示.点A 在第一象限,点B 在第二象限,点C在第三象限,点D在第四象限.
已知在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是________.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐标为正,可得关于m的一元一次不等式组 解得m>2.
m>2
三.利用平面直角坐标系内点的坐标确定字母的值
长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为
(-2,-3).请你写出另外三个
顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为
B(2,-3),C(2,3),D(-2,3).
四.建立平面坐标系确定点的坐标
A
B
C
D
O
东
北
50
50
单位:m
张明
李强同学家在学校以东100m再往北150m处,张明同学家在学校以西100m再往南50m处,王玲同学家在学校以南150m处,如图,在坐标系中画出这三位同学家的位置,并用坐标表示出来.
李强
王玲
(100,150)
(-100,-50)
(0,-150)
学校
根据以下条件画一幅示意图, 标出学校、书店、电影院、汽车站的位置.
(1)从学校向东走500m,再向北走450m到书店.
(2)从学校向西走300m,再向南走300m,最后向东走50m到电影院.
(3)从学校向南走600m,再向东走400m到汽车站.
五.建立平面直角坐标系确定点的位置
解:如图,以学校所在位置为原点,分别以正东、正北方向为x 轴,y 轴的正方向,建立平面直角坐标系,规定1个单位长度代表100m长.根据题目条件,点A(5,4.5)是书店的位置,点B(-2.5,-3)是电影院的位置,点C(4,-6) 是汽车站的位置.
如图,是某次海战中敌我双方舰艇对峙示意图(图中1cm表示20 n mile),对我方潜艇O来说:
O
六.用方位角和距离表示物体位置
敌方
舰艇 C
敌方
舰艇 A
敌方舰艇 B
小岛
40
O
1cm
1cm
(1) 北偏东40°的方向上有哪些目标 要想确定敌舰B的位置,还需要什么数据
解:有敌方舰艇B和小岛;还需要敌方舰艇B与我方潜艇O的距离.
(2) 距离我方潜艇
20 n mile的敌舰有
哪几艘
解:有敌舰A和敌舰C.
解:(3)要确定每艘敌舰的位置,各需要两个数据:距离和方位角.如,对我方潜艇O来说,敌舰A在正南方向,图上距离为1cm处;
敌舰B在北偏东40°
方向,图上距离
为1.4cm处;
敌舰C在正东方向,
图上距离为1cm处.
敌方
舰艇 C
敌方
舰艇 A
敌方舰艇 B
40
O
1cm
1cm
(3) 要确定每艘敌舰的位置,各需要几个数据
1.4cm
长方形零件如图1(单位:mm),建立适当的坐标系,用坐标表示孔心的位置.如图2,货轮与灯塔相距40 n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
图1
图2
解:1、以长方形左下角的顶点为原点,长所在的直线为x轴(向右为正方向),宽所在的直线为y轴(向上为正方向)建立直角坐标系,则孔心的坐标是(15,25).
2、灯塔在货轮的南偏东500 ,40n mile处,货轮在灯塔的北偏西500 ,40n mile处.
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
提示:左减右加,下减上加.
七.平面直角坐标系内点的平移
①将点(2,1)向右平移3个单位长度,
可以得到对应点坐标__________ ;
②将点(2,-1)向左平移3个单位长度,
可以得到对应点坐标__________ ;
③将点(2,5)向上平移3个单位长度,
可以得到对应点坐标__________ ;
④将点(-2,5)向下平移3单位长度,
可以得到对应点坐标__________.
(5,1)
(-1,-1)
(2,8)
(-2,2)
根据平移填空:
如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的三角
形A1B1C1,并写出点A、C、
A1、C1的坐标;
1
y
O
1
x
A
B
C
A1
B1
C1
解:(1)三角形A1B1C1如图所示,各点的坐标分别为A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
P
P1
八.平面直角坐标系内图形的平移
C
1
y
O
1
x
A
B
C
A1
B1
C1
(2) 求出以A、C、A1、C1为顶点的四边形的面积.
解:(2)连接AA1,CC1,
P
P1
如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
A′
B′
C′
D′
解:如图所示,四边形A′B′C′D′就是所要画的四边形,
A′(-3,1), B′(1,1), C′(2,4), D′(-2,4).
在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点A1(-2,2)处,则点B的对应点B1的坐标为( )
A.(-1,-1) B.(1,0)
C.(-1,0) D.(3,0)
A
C
如图所示,将点A向右平移( )个单位长度可得到点B .
A.3个单位长度 B. 4个单位长度 C.5个单位长度 D.6个单位长度
如图所示,将点A向下平移5个单位长度后,将重合于图中的 ( )
A.点C B.点F
C.点D D.点E
B
D
F
y
x
0
-4
-3
-2
-1
1
2
3
4
1
2
3
4
-1
-2
-3
-4
C
D
A
B
E
G
如图所示,点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G′,则G′的坐标为( )
A.(6,5) B.(4,5) C.(6,3) D.(4,3)
D
F
y
x
0
-4
-3
-2
-1
1
2
3
4
1
2
3
4
-1
-2
-3
-4
C
D
A
B
E
G
如图所示,将点A先向右平移3个单位长度,再向下平移5个单位长度,得到A′为__________;将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B′为________,则A′与B′相距____个单位长度.
(0,-3)
(4,-3)
4
F
y
x
0
-4
-3
-2
-1
1
2
3
4
1
2
3
4
-1
-2
-3
-4
C
D
A
B
E
G
已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为____________________;
已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为___________________.
(-1,-2)或(-1,6)
(3,2)或(-5,2)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6);B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3);C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
C
O
A1
C1
B1
