2021-2022学年人教版八年级数学上册13.1 轴对称 同步培优(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.1 轴对称 同步培优(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 23:36:23 | ||
图片预览


文档简介
人教版 八年级数学上册 13.1 轴对称 同步培优
一、选择题
1. 如果点(m-1,-1)与点(5,-1)关于y轴对称,那么m的值为( )
A.4 B.-4 C.5 D.-5
2. 如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′ B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线 D.直线BC和B′C′的交点不在直线l上
3. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
4. 如图,在△ABC中,∠ACB=90°,∠B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是( )
A.∠ADC=45° B.∠DAC=45°
C.BD=AD D.BD=DC
5. 将平面直角坐标系内某个图形的各个点的横坐标都乘-1,纵坐标不变,则所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.图形向左平移 D.图形向下平移
6. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
7. 如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,∠EAF的度数为( )
A.113° B.124°
C.129° D.134°
8. 如图,点P在直线l外,以点P为圆心,大于点P到直线l的距离为半径画弧,交直线l于点A,B;保持半径不变,分别以点A,B为圆心画弧,两弧相交于点Q,则PQ⊥l.上述尺规作图的依据是 ( )
A.一条直线与两平行线中的一条垂直,必然与另一条直线也垂直
B.线段垂直平分线上的点与这条线段两个端点的距离相等,两点确定一条直线
C.与线段两个端点距离相等的点在这条线段的垂直平分线上,两点确定一条直线
D.角的内部到角的两边的距离相等的点在角的平分线上
二、填空题
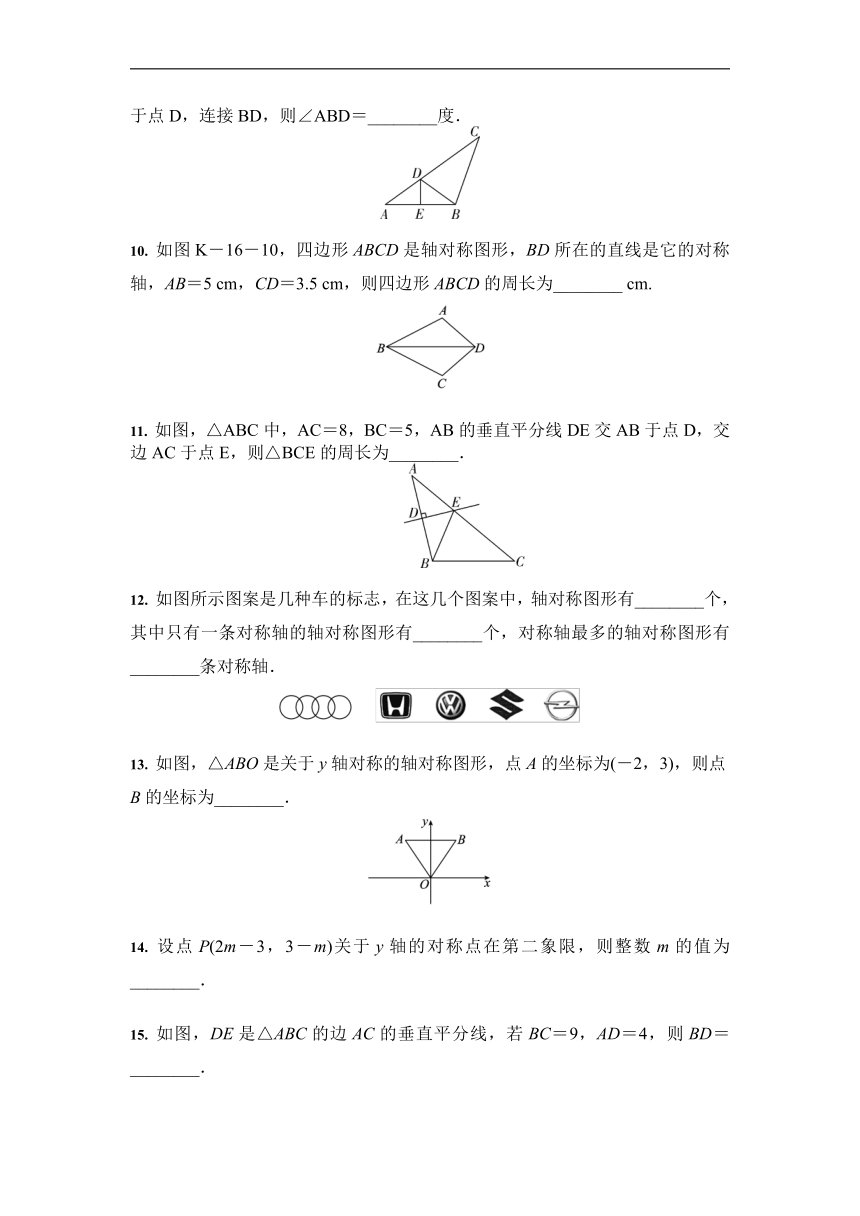
9. 如图,在△ABC中,AB=BC,∠ABC=110°.AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=________度.
10. 如图K-16-10,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5 cm,CD=3.5 cm,则四边形ABCD的周长为________ cm.
11. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
12. 如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
13. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
14. 设点P(2m-3,3-m)关于y轴的对称点在第二象限,则整数m的值为________.
15. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.
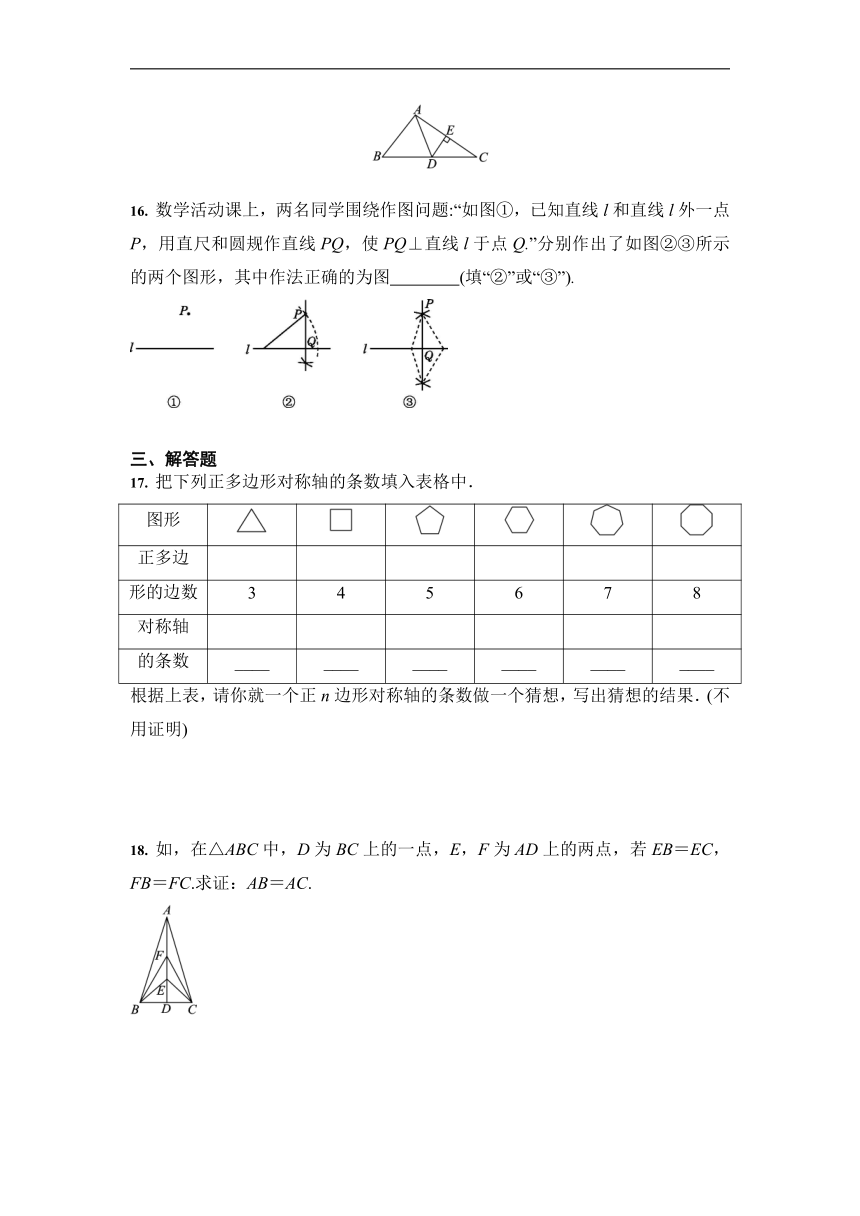
16. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图 (填“②”或“③”).
三、解答题
17. 把下列正多边形对称轴的条数填入表格中.
图形
正多边
形的边数 3 4 5 6 7 8
对称轴
的条数 ____ ____ ____ ____ ____ ____
根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)
18. 如,在△ABC中,D为BC上的一点,E,F为AD上的两点,若EB=EC,FB=FC.求证:AB=AC.
19. 如图,在△ABC中,边AC的垂直平分线分别交AB,AC于点E,D.
(1)若AC=8,△BEC的周长为18,求△ABC的周长;
(2)若AB-BC=6,△BEC的周长为16,求AB,BC的长.
20. 如图1,△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
人教版 八年级数学上册 13.1 轴对称 同步培优-答案
一、选择题
1. 【答案】B [解析] ∵点(m-1,-1)与点(5,-1)关于y轴对称,∴m-1=-5,解得m=-4.
2. 【答案】D
3. 【答案】D [解析] 点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).
4. 【答案】D [解析] ∵AB的垂直平分线交BC于点D,∴AD=BD,故C正确;∵AD=BD,∴∠B=∠BAD=22.5°.∴∠ADC=45°,故A正确;∠DAC=90°-∠ADC=90°-45°=45°,故B正确.故选D.
5. 【答案】B [解析] 点的横坐标乘-1后变为原来的相反数,又因为纵坐标不变,故变化后的点与原来的点关于y轴对称.
6. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
7. 【答案】D [解析] 连接AD.
∵点D分别以AB,AC为对称轴,画出对称点E,F,∴∠EAB=∠BAD,∠FAC=∠CAD.
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠CAD=67°.
∴∠EAF=2∠BAC=134°.
8. 【答案】C
二、填空题
9. 【答案】35 【解析】∵AB=BC,∠ABC=110°,∴∠A=∠C=35°,∵DE垂直平分AB,∴DA=DB,∴∠ABD=∠A=35°.
10. 【答案】17
11. 【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
12. 【答案】3 2 2
13. 【答案】(2,3) [解析] ∵△ABO是关于y轴对称的轴对称图形,∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).
14. 【答案】2 [解析] 由于点P关于y轴的对称点在第二象限,则点P在第一象限.
依题意有解得因为m为整数,所以m=2.
15. 【答案】5
16. 【答案】③
三、解答题
17. 【答案】
解:3 4 5 6 7 8
猜想:一个正n边形有n条对称轴.
18. 【答案】
证明:∵EB=EC,∴点E在BC的垂直平分线上.∵FB=FC,∴点F在BC的垂直平分线上.∴直线EF是BC的垂直平分线.∵点A在直线EF上,∴AB=AC.
19. 【答案】
解:(1)∵DE垂直平分AC,
∴CE=AE.
∵△BEC的周长为18,
∴BE+BC+CE=BE+AE+BC=AB+BC=18.
∴△ABC的周长=AB+BC+AC=18+8=26.
(2)∵△BEC的周长为16,
∴AB+BC=16.
又∵AB-BC=6,
∴AB=11,BC=5.
20. 【答案】
解:(1)∵∠BAC=50°,AD平分∠BAC,
∴∠EAD=∠BAC=25°.
∵DE⊥AB,
∴∠AED=90°.
∴∠EDA=90°-25°=65°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB.
∵AD平分∠BAC,
∴∠DAE=∠DAC.
又∵AD=AD,
∴△AED≌△ACD.
∴AE=AC,DE=DC.
∴点A,D都在线段CE的垂直平分线上.
∴直线AD是线段CE的垂直平分线.
一、选择题
1. 如果点(m-1,-1)与点(5,-1)关于y轴对称,那么m的值为( )
A.4 B.-4 C.5 D.-5
2. 如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′ B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线 D.直线BC和B′C′的交点不在直线l上
3. 在平面直角坐标系中,作点A(3,4)关于x轴的对称点A′,再将点A′向左平移6个单位长度,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3)
C.(-3,4) D.(-3,-4)
4. 如图,在△ABC中,∠ACB=90°,∠B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是( )
A.∠ADC=45° B.∠DAC=45°
C.BD=AD D.BD=DC
5. 将平面直角坐标系内某个图形的各个点的横坐标都乘-1,纵坐标不变,则所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.图形向左平移 D.图形向下平移
6. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
7. 如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,∠EAF的度数为( )
A.113° B.124°
C.129° D.134°
8. 如图,点P在直线l外,以点P为圆心,大于点P到直线l的距离为半径画弧,交直线l于点A,B;保持半径不变,分别以点A,B为圆心画弧,两弧相交于点Q,则PQ⊥l.上述尺规作图的依据是 ( )
A.一条直线与两平行线中的一条垂直,必然与另一条直线也垂直
B.线段垂直平分线上的点与这条线段两个端点的距离相等,两点确定一条直线
C.与线段两个端点距离相等的点在这条线段的垂直平分线上,两点确定一条直线
D.角的内部到角的两边的距离相等的点在角的平分线上
二、填空题
9. 如图,在△ABC中,AB=BC,∠ABC=110°.AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=________度.
10. 如图K-16-10,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5 cm,CD=3.5 cm,则四边形ABCD的周长为________ cm.
11. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
12. 如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
13. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.
14. 设点P(2m-3,3-m)关于y轴的对称点在第二象限,则整数m的值为________.
15. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.
16. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图 (填“②”或“③”).
三、解答题
17. 把下列正多边形对称轴的条数填入表格中.
图形
正多边
形的边数 3 4 5 6 7 8
对称轴
的条数 ____ ____ ____ ____ ____ ____
根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)
18. 如,在△ABC中,D为BC上的一点,E,F为AD上的两点,若EB=EC,FB=FC.求证:AB=AC.
19. 如图,在△ABC中,边AC的垂直平分线分别交AB,AC于点E,D.
(1)若AC=8,△BEC的周长为18,求△ABC的周长;
(2)若AB-BC=6,△BEC的周长为16,求AB,BC的长.
20. 如图1,△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
人教版 八年级数学上册 13.1 轴对称 同步培优-答案
一、选择题
1. 【答案】B [解析] ∵点(m-1,-1)与点(5,-1)关于y轴对称,∴m-1=-5,解得m=-4.
2. 【答案】D
3. 【答案】D [解析] 点A(3,4)关于x轴的对称点A′的坐标为(3,-4),将点A′向左平移6个单位长度,得到点B(-3,-4).
4. 【答案】D [解析] ∵AB的垂直平分线交BC于点D,∴AD=BD,故C正确;∵AD=BD,∴∠B=∠BAD=22.5°.∴∠ADC=45°,故A正确;∠DAC=90°-∠ADC=90°-45°=45°,故B正确.故选D.
5. 【答案】B [解析] 点的横坐标乘-1后变为原来的相反数,又因为纵坐标不变,故变化后的点与原来的点关于y轴对称.
6. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
7. 【答案】D [解析] 连接AD.
∵点D分别以AB,AC为对称轴,画出对称点E,F,∴∠EAB=∠BAD,∠FAC=∠CAD.
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠CAD=67°.
∴∠EAF=2∠BAC=134°.
8. 【答案】C
二、填空题
9. 【答案】35 【解析】∵AB=BC,∠ABC=110°,∴∠A=∠C=35°,∵DE垂直平分AB,∴DA=DB,∴∠ABD=∠A=35°.
10. 【答案】17
11. 【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
12. 【答案】3 2 2
13. 【答案】(2,3) [解析] ∵△ABO是关于y轴对称的轴对称图形,∴点A(-2,3)与点B关于y轴对称.∴点B的坐标为(2,3).
14. 【答案】2 [解析] 由于点P关于y轴的对称点在第二象限,则点P在第一象限.
依题意有解得
15. 【答案】5
16. 【答案】③
三、解答题
17. 【答案】
解:3 4 5 6 7 8
猜想:一个正n边形有n条对称轴.
18. 【答案】
证明:∵EB=EC,∴点E在BC的垂直平分线上.∵FB=FC,∴点F在BC的垂直平分线上.∴直线EF是BC的垂直平分线.∵点A在直线EF上,∴AB=AC.
19. 【答案】
解:(1)∵DE垂直平分AC,
∴CE=AE.
∵△BEC的周长为18,
∴BE+BC+CE=BE+AE+BC=AB+BC=18.
∴△ABC的周长=AB+BC+AC=18+8=26.
(2)∵△BEC的周长为16,
∴AB+BC=16.
又∵AB-BC=6,
∴AB=11,BC=5.
20. 【答案】
解:(1)∵∠BAC=50°,AD平分∠BAC,
∴∠EAD=∠BAC=25°.
∵DE⊥AB,
∴∠AED=90°.
∴∠EDA=90°-25°=65°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB.
∵AD平分∠BAC,
∴∠DAE=∠DAC.
又∵AD=AD,
∴△AED≌△ACD.
∴AE=AC,DE=DC.
∴点A,D都在线段CE的垂直平分线上.
∴直线AD是线段CE的垂直平分线.
