沪科版九年级数学下册24.5 三角形的内切圆练习题 (word版含解析)
文档属性
| 名称 | 沪科版九年级数学下册24.5 三角形的内切圆练习题 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 205.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 08:22:37 | ||
图片预览



文档简介
三角形的内切圆练习题
如图,等腰的内切圆与,,分别相切于点,,,且,,则的长是
B. C. D.
如图,的内切圆与、、分别相切于点、、,且,,,则阴影部分即四边形的面积是
B. C. D.
如图,在中,点为的内心,,,则的面积是
B. C. D.
如图,是等边的内切圆,分别切,,于点,,,是上一点,则的度数是
A. B. C. D.
已知一个三角形的三边长分别为、、,则其内切圆的半径为
A. B. C. D.
如图,在中,点是的内心,连接,,过点作分别交,于点,已知的周长为,,的周长为,则表示与的函数图象大致是
A. B.
C. D.
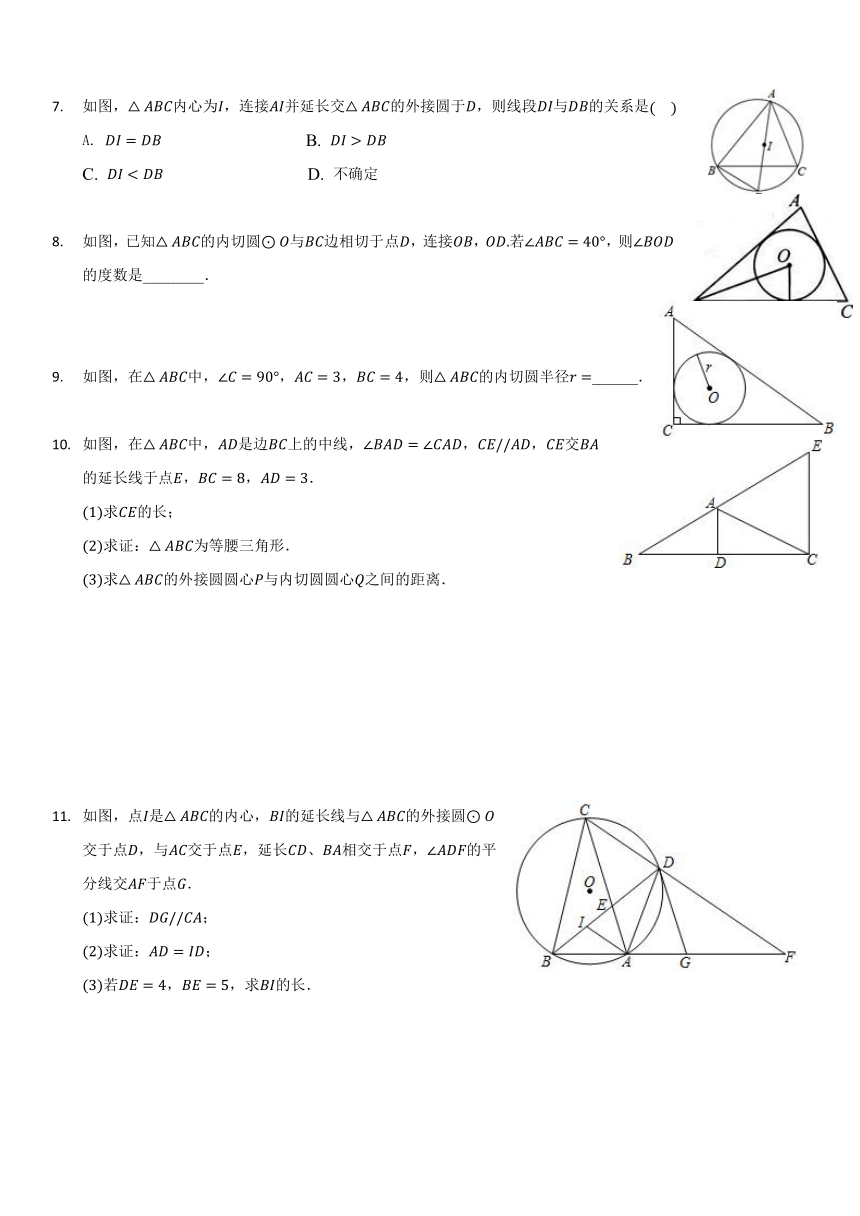
如图,内心为,连接并延长交的外接圆于,则线段与的关系是
B.
C. D. 不确定
如图,已知的内切圆与边相切于点,连接,若,则的度数是________.
如图,在中,,,,则的内切圆半径______.
如图,在中,是边上的中线,,,交的延长线于点,,.
求的长;
求证:为等腰三角形.
求的外接圆圆心与内切圆圆心之间的距离.
如图,点是的内心,的延长线与的外接圆交于点,与交于点,延长、相交于点,的平分线交于点.
求证:;
求证:;
若,,求的长.
如图,是的切线,切点为,是的直径,连接交于过点作于点,交于,连接,.
求证:是的切线;
求证:为的内心;
若,,求的长.
如图,已知内接于,是的直径,的平分线交于点,交于点,连接,作,交的延长线于点.
求证:是的切线;
若,,求的半径和的长.
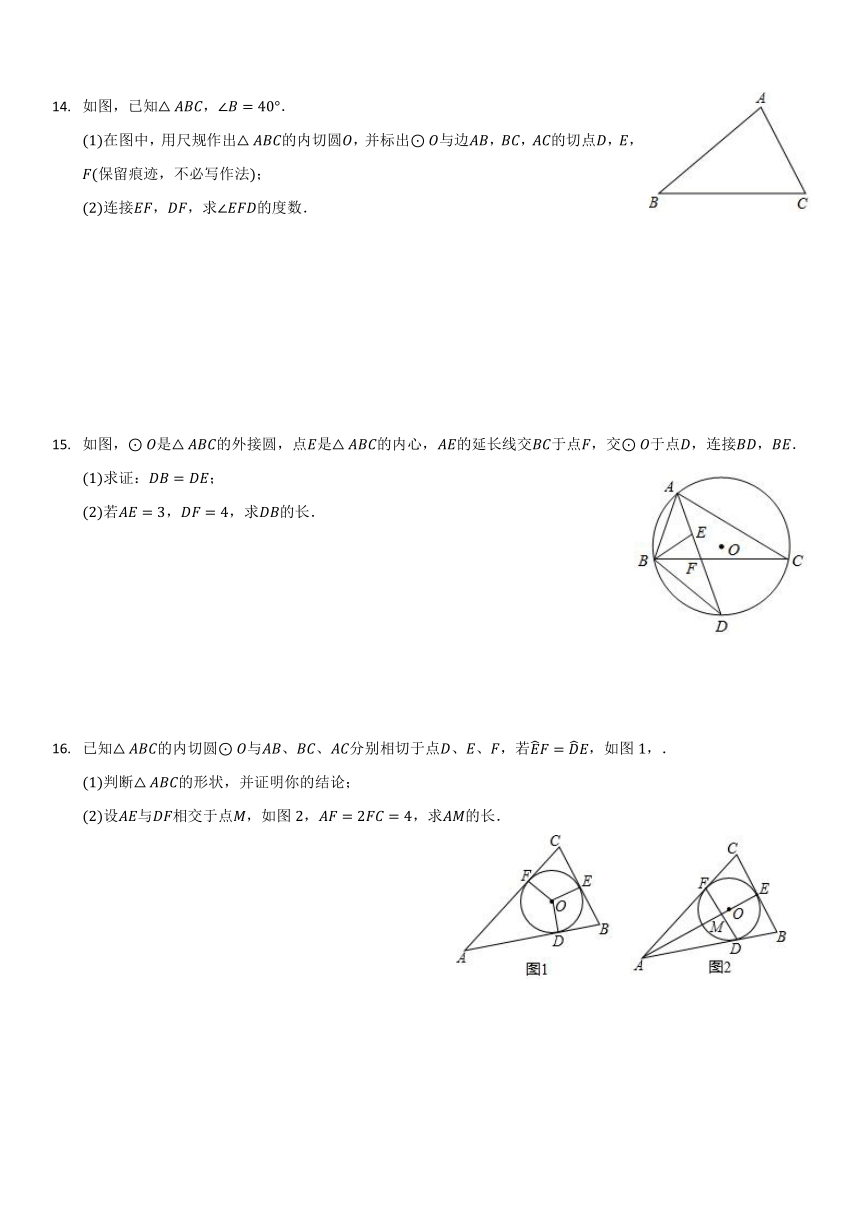
如图,已知,.
在图中,用尺规作出的内切圆,并标出与边,,的切点,,保留痕迹,不必写作法;
连接,,求的度数.
如图,是的外接圆,点是的内心,的延长线交于点,交于点,连接,.
求证:;
若,,求的长.
已知的内切圆与、、分别相切于点、、,若,如图,.
判断的形状,并证明你的结论;
设与相交于点,如图,,求的长.
答案
1.【答案】
解:连接、、、,交于,如图,
等腰的内切圆与,,分别相切于点,,,
平分,,,,
,
,
点、、共线,即,
,
在中,,
,
,
设的半径为,则,,
在中,,解得,
在中,,
,,
垂直平分,
,,
,
,
.
故选:.
2.【答案】
【解析】解:,,,
,
为直角三角形,,
、与分别相切于点、
,,
四边形为正方形,
设,
则,
的内切圆与、、分别相切于点、、,
,,
,
,
阴影部分即四边形的面积是.
故选:.
3.【答案】
【解析】解:过点作于点.
点为的内心,,
,
,
则,
,
,,
,
的面积,
故选:.
4.【答案】
解:如图,连接,.
是的内切圆,,是切点,
,,
,
是等边三角形,
,
,
,
故选:.
5.【答案】
解:如图,,,,内切圆的半径为,切点为、、,作于,设,则.
由勾股定理可知:,
即,解得,
,
,
,
,
故选:.
6.【答案】
解:点是的内心,
,,
,
,,
,,
,,
的周长,
的周长为,,
,
,
,
,
,
,
即与的函数关系式为,
故选:.
7.【答案】
【解析】解:连接,如图,
内心为,
,,
,
,
,
即,
.
故选:.
8.【答案】
【解析】解:的内切圆与边相切于点,
平分,,
,
.
故答案为.
9.【答案】
【解析】解:在中,,,,
根据勾股定理,得,
如图,设的内切圆与三条边的切点分别为、、,
连接、、,
,,,
可得矩形,
根据切线长定理,得
,
矩形是正方形,
,
,
,
,
,
解得.
则的内切圆半径.
故答案为:.
10.【答案】解:是边上的中线,
,
,
为的中位线,
;
证明:,
,,
而,
,
,
而,
,
为等腰三角形.
如图,连接、、,
在中,,
设的半径为,的半径为,
在中,,解得,
,
,
,解得,
即,
.
答:的外接圆圆心与内切圆圆心之间的距离为.
11.【答案】证明:点是的内心,
,
平分,
,
,
,
,
,
;
证明:点是的内心,
,
,
即,
;
解:,,
∽,
::,即::,
,
,
.
12.【答案】证明:连接,
为的直径,
,
,
,,
,
,
,
在和中,
,
≌,
,
为的切线,
,
,
是的切线;
证明:连接,
为的切线,
,
,
,
,
,
,即平分,
、为的切线,
平分
为的内心;
解:,,
,
,
在中,,
,,
,,
∽,
,
.
13.【答案】证明:连接,
是的直径,
,
即,
平分,
,
,
,
,
,
,
,
,
,
是的半径,
是的切线;
解:如图,设的半径为,则,
,
在中,由勾股定理得:,
,
解得:,
的半径为;
,,
∽,
,
设,则,
由勾股定理得:,
即,
解得:,
,
,
,
,
,
,
,即,
.
14.【答案】解:如图,
即为所求.
如图,
连接,,
,,
,
,
,
.
15.【答案】证明:点是的内心,
平分,平分,
,,
又与所对弧为,
.
,,
即,
故DB.
解:,,
∽,
,
,,设,
由可得,
则式化为,
解得:,不符题意,舍去,
则.
16.【答案】解:为等腰三角形,
的内切圆与、、分别相切于点、、,
,
四边形内角和为,
,,
,
,
,,
为等腰三角形;
连接、、、,如图,
等腰三角形中,,
是中点,,
在和中,,
≌,
,
同理≌,,
≌,,
,,
,
,
,
.
如图,等腰的内切圆与,,分别相切于点,,,且,,则的长是
B. C. D.
如图,的内切圆与、、分别相切于点、、,且,,,则阴影部分即四边形的面积是
B. C. D.
如图,在中,点为的内心,,,则的面积是
B. C. D.
如图,是等边的内切圆,分别切,,于点,,,是上一点,则的度数是
A. B. C. D.
已知一个三角形的三边长分别为、、,则其内切圆的半径为
A. B. C. D.
如图,在中,点是的内心,连接,,过点作分别交,于点,已知的周长为,,的周长为,则表示与的函数图象大致是
A. B.
C. D.
如图,内心为,连接并延长交的外接圆于,则线段与的关系是
B.
C. D. 不确定
如图,已知的内切圆与边相切于点,连接,若,则的度数是________.
如图,在中,,,,则的内切圆半径______.
如图,在中,是边上的中线,,,交的延长线于点,,.
求的长;
求证:为等腰三角形.
求的外接圆圆心与内切圆圆心之间的距离.
如图,点是的内心,的延长线与的外接圆交于点,与交于点,延长、相交于点,的平分线交于点.
求证:;
求证:;
若,,求的长.
如图,是的切线,切点为,是的直径,连接交于过点作于点,交于,连接,.
求证:是的切线;
求证:为的内心;
若,,求的长.
如图,已知内接于,是的直径,的平分线交于点,交于点,连接,作,交的延长线于点.
求证:是的切线;
若,,求的半径和的长.
如图,已知,.
在图中,用尺规作出的内切圆,并标出与边,,的切点,,保留痕迹,不必写作法;
连接,,求的度数.
如图,是的外接圆,点是的内心,的延长线交于点,交于点,连接,.
求证:;
若,,求的长.
已知的内切圆与、、分别相切于点、、,若,如图,.
判断的形状,并证明你的结论;
设与相交于点,如图,,求的长.
答案
1.【答案】
解:连接、、、,交于,如图,
等腰的内切圆与,,分别相切于点,,,
平分,,,,
,
,
点、、共线,即,
,
在中,,
,
,
设的半径为,则,,
在中,,解得,
在中,,
,,
垂直平分,
,,
,
,
.
故选:.
2.【答案】
【解析】解:,,,
,
为直角三角形,,
、与分别相切于点、
,,
四边形为正方形,
设,
则,
的内切圆与、、分别相切于点、、,
,,
,
,
阴影部分即四边形的面积是.
故选:.
3.【答案】
【解析】解:过点作于点.
点为的内心,,
,
,
则,
,
,,
,
的面积,
故选:.
4.【答案】
解:如图,连接,.
是的内切圆,,是切点,
,,
,
是等边三角形,
,
,
,
故选:.
5.【答案】
解:如图,,,,内切圆的半径为,切点为、、,作于,设,则.
由勾股定理可知:,
即,解得,
,
,
,
,
故选:.
6.【答案】
解:点是的内心,
,,
,
,,
,,
,,
的周长,
的周长为,,
,
,
,
,
,
,
即与的函数关系式为,
故选:.
7.【答案】
【解析】解:连接,如图,
内心为,
,,
,
,
,
即,
.
故选:.
8.【答案】
【解析】解:的内切圆与边相切于点,
平分,,
,
.
故答案为.
9.【答案】
【解析】解:在中,,,,
根据勾股定理,得,
如图,设的内切圆与三条边的切点分别为、、,
连接、、,
,,,
可得矩形,
根据切线长定理,得
,
矩形是正方形,
,
,
,
,
,
解得.
则的内切圆半径.
故答案为:.
10.【答案】解:是边上的中线,
,
,
为的中位线,
;
证明:,
,,
而,
,
,
而,
,
为等腰三角形.
如图,连接、、,
在中,,
设的半径为,的半径为,
在中,,解得,
,
,
,解得,
即,
.
答:的外接圆圆心与内切圆圆心之间的距离为.
11.【答案】证明:点是的内心,
,
平分,
,
,
,
,
,
;
证明:点是的内心,
,
,
即,
;
解:,,
∽,
::,即::,
,
,
.
12.【答案】证明:连接,
为的直径,
,
,
,,
,
,
,
在和中,
,
≌,
,
为的切线,
,
,
是的切线;
证明:连接,
为的切线,
,
,
,
,
,
,即平分,
、为的切线,
平分
为的内心;
解:,,
,
,
在中,,
,,
,,
∽,
,
.
13.【答案】证明:连接,
是的直径,
,
即,
平分,
,
,
,
,
,
,
,
,
,
是的半径,
是的切线;
解:如图,设的半径为,则,
,
在中,由勾股定理得:,
,
解得:,
的半径为;
,,
∽,
,
设,则,
由勾股定理得:,
即,
解得:,
,
,
,
,
,
,
,即,
.
14.【答案】解:如图,
即为所求.
如图,
连接,,
,,
,
,
,
.
15.【答案】证明:点是的内心,
平分,平分,
,,
又与所对弧为,
.
,,
即,
故DB.
解:,,
∽,
,
,,设,
由可得,
则式化为,
解得:,不符题意,舍去,
则.
16.【答案】解:为等腰三角形,
的内切圆与、、分别相切于点、、,
,
四边形内角和为,
,,
,
,
,,
为等腰三角形;
连接、、、,如图,
等腰三角形中,,
是中点,,
在和中,,
≌,
,
同理≌,,
≌,,
,,
,
,
,
.
