北师大版九年级数学下册第3章圆解答题专题提升训练(word版含解析)
文档属性
| 名称 | 北师大版九年级数学下册第3章圆解答题专题提升训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 660.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 08:39:30 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》解答题专题提升训练(附答案)
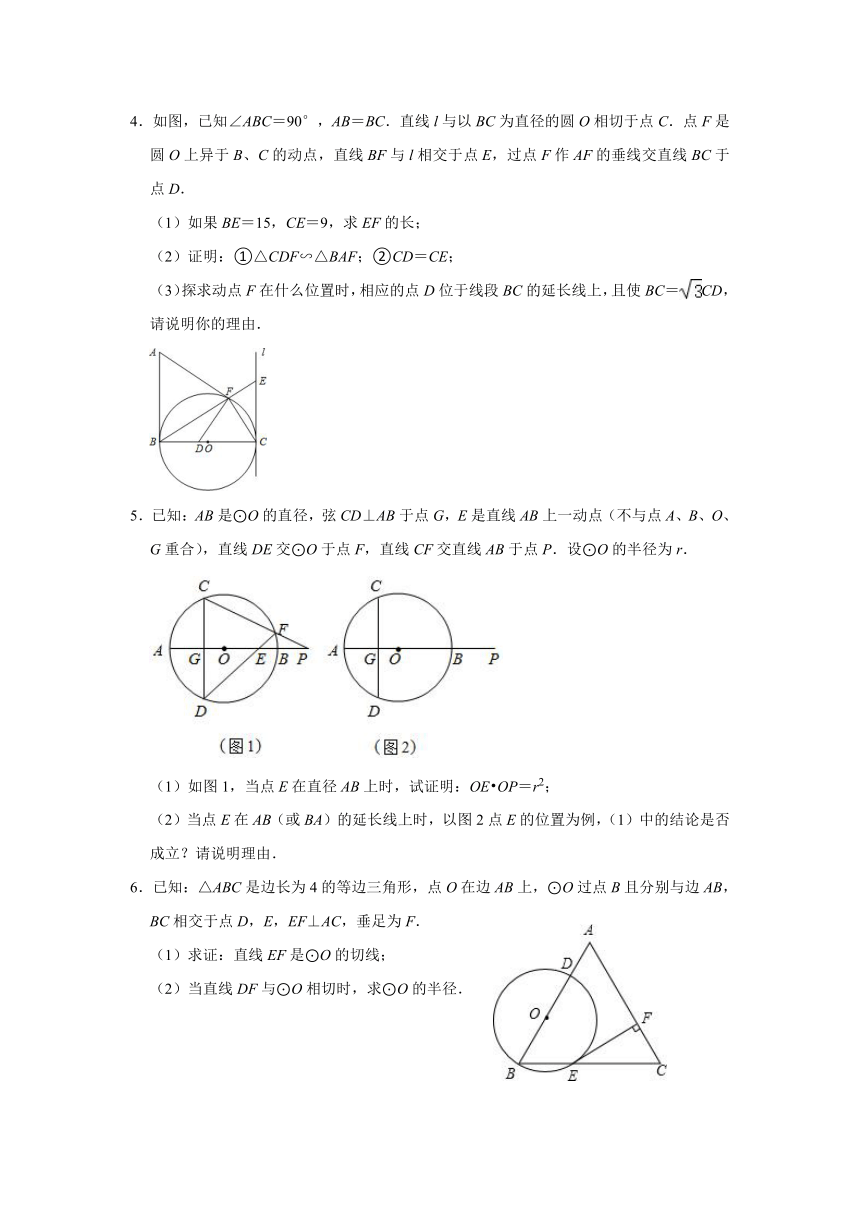
1.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
2.已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过点P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)当点P在线段AB上时(如图).求证:PA PB=PE PF;
(2)当点P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明;如果不成立,请说明理由;
(3)若,,求⊙O的半径.
3.如图,在△ABC中,AB=5,AC=6,BC=7.
(1)求sinA和sinC的值;
(2)若⊙D的圆心D在边AC上,且⊙D与边AB、BC都相切,求⊙D的半径.
4.如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC于点D.
(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使BC=CD,请说明你的理由.
5.已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、O、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE OP=r2;
(2)当点E在AB(或BA)的延长线上时,以图2点E的位置为例,(1)中的结论是否成立?请说明理由.
6.已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
7.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连接BD,过点E作EM∥BD,交BA的延长线于点M.
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.
8.如图,AB是半圆O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO面积相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.
9.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB等于 (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似?请写出解答过程.
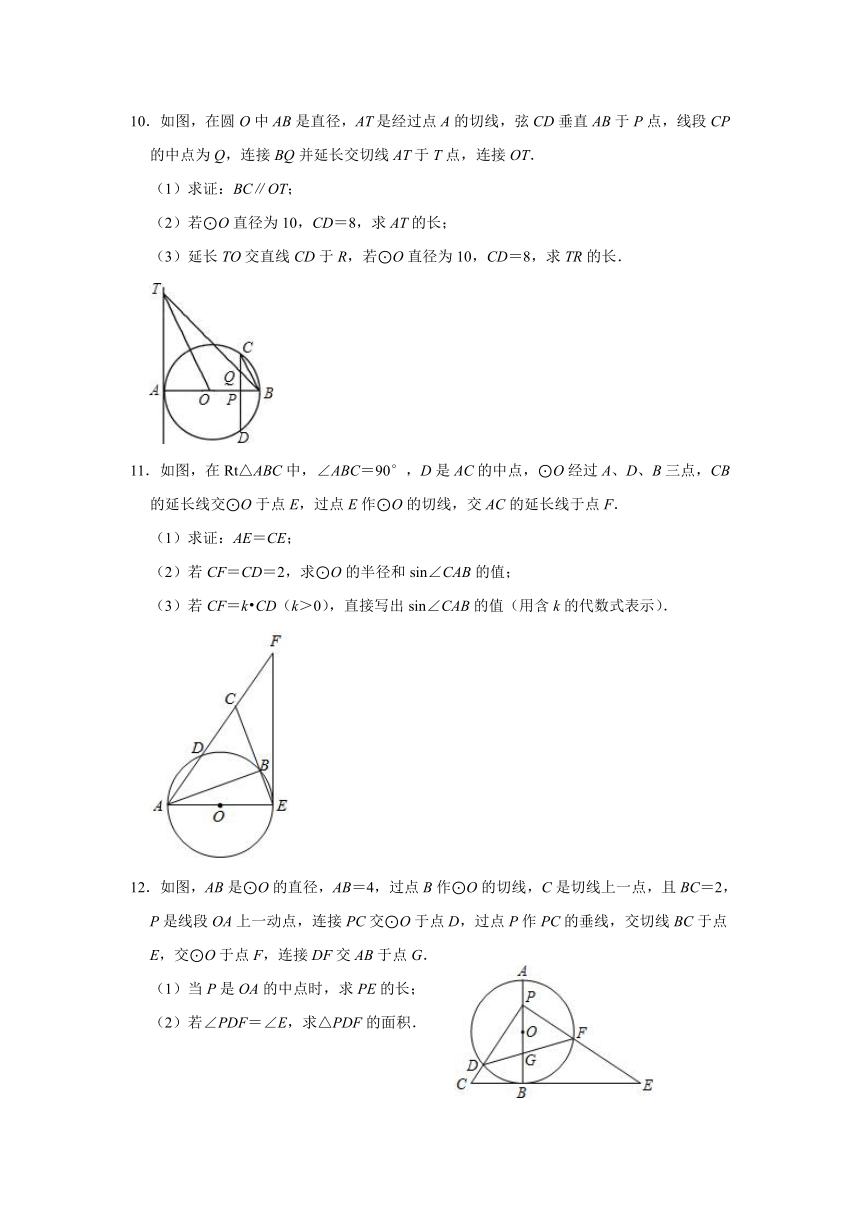
10.如图,在圆O中AB是直径,AT是经过点A的切线,弦CD垂直AB于P点,线段CP的中点为Q,连接BQ并延长交切线AT于T点,连接OT.
(1)求证:BC∥OT;
(2)若⊙O直径为10,CD=8,求AT的长;
(3)延长TO交直线CD于R,若⊙O直径为10,CD=8,求TR的长.
11.如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E,过点E作⊙O的切线,交AC的延长线于点F.
(1)求证:AE=CE;
(2)若CF=CD=2,求⊙O的半径和sin∠CAB的值;
(3)若CF=k CD(k>0),直接写出sin∠CAB的值(用含k的代数式表示).
12.如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA上一动点,连接PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连接DF交AB于点G.
(1)当P是OA的中点时,求PE的长;
(2)若∠PDF=∠E,求△PDF的面积.
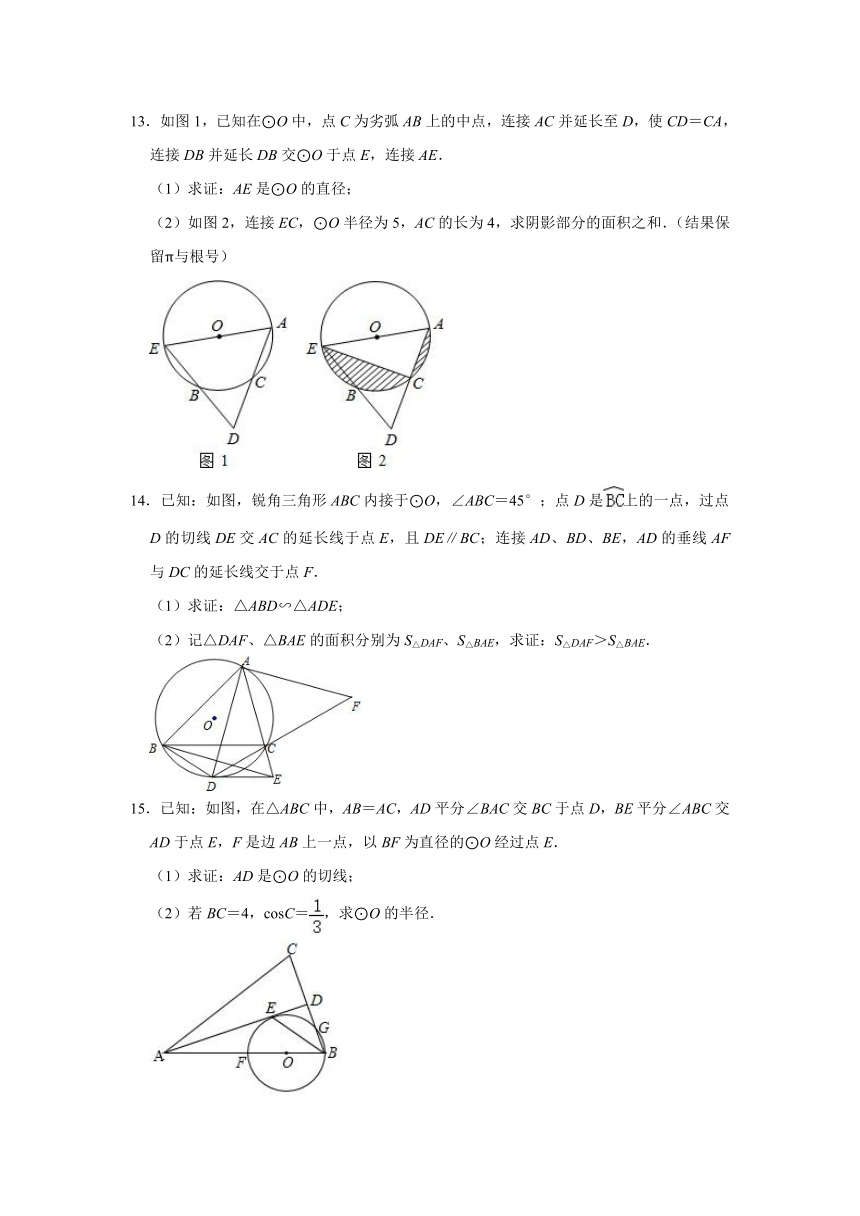
13.如图1,已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,连接DB并延长DB交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图2,连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和.(结果保留π与根号)
14.已知:如图,锐角三角形ABC内接于⊙O,∠ABC=45°;点D是上的一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连接AD、BD、BE,AD的垂线AF与DC的延长线交于点F.
(1)求证:△ABD∽△ADE;
(2)记△DAF、△BAE的面积分别为S△DAF、S△BAE,求证:S△DAF>S△BAE.
15.已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E,F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC=,求⊙O的半径.
16.已知:如图,AB是⊙O的直径,点P为BA延长线上一点,PC为⊙O的切线,C为切点,BD⊥PC,垂足为D,交⊙O于E,连接AC、BC、EC.
(1)求证:BC2=BD BA;
(2)若AC=6,DE=4,求PC的长.
17.已知:如图.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)若⊙O的半径为5,AF=,求tan∠ABF的值.
18.如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B.
(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2,求tan∠OAC的值.
19.如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
(1)求证:D是的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若,且AC=4,求CF的长.
20.如图1,梯形ABCD中,AD∥BC,AB=8,∠ABC=90°,以AB为直径的⊙O切CD于点E.
(1)若设AD=x,BC=y,试求出y与x之间的函数关系式;
(2)如图2,BE的延长线交AD的延长线于点F.求证:AD=AF;
(3)如图3,若AD=2,BC=8.动点P以每秒1个单位长的速度,从点B沿线段BC向点C运动;同时点Q以相同的速度,从点D沿折线D﹣A﹣B向点B运动.当点P到达点C时,两点同时停止运动.过点P作直线PM⊥BC与折线B﹣D﹣C的交点为M.点P运动的时间为t(秒).点P在线段BC上运动时,是否可以使得以D、M、Q为顶点的三角形为直角三角形,若可以,请求出t的值;若不可以,请说明理由.
参考答案
1.(1)证明:连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴PB∥OC,
∵CD⊥PA,
∴CD⊥OC,CO为⊙O半径,
∴CD为⊙O的切线;
(2)解:过O作OF⊥AB,垂足为F,
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形DCOF为矩形,
∴OC=FD,OF=CD.
∵DC+DA=6,
设AD=x,则OF=CD=6﹣x,
∵⊙O的直径为10,
∴DF=OC=5,
∴AF=5﹣x,
在Rt△AOF中,由勾股定理得AF2+OF2=OA2.
即(5﹣x)2+(6﹣x)2=25,
化简得x2﹣11x+18=0,
解得x1=2,x2=9.
∵CD=6﹣x大于0,故x=9舍去,
∴x=2,
从而AD=2,AF=5﹣2=3,
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴AB=2AF=6.
2.(1)证明:∵BT切⊙O于点B,
∴∠EBA=∠C,
∵EF∥BC,
∴∠AFP=∠C,
∠AFP=∠EBP,
∵∠APF=∠EPB,
∴△PFA∽△PBE,
∴,
∴PA PB=PE PF;
(2)解:当P为BA延长线上一点时,第(1)题的结论仍成立(如图)
∵BT切⊙O于点B,
∴∠EBA=∠C,
∵EF∥BC,
∴∠PFA=∠C,
∠PFA=∠PBE,
又∵∠APF=∠EPB,
∴△PFA∽△PBE,
∴,
∴PA PB=PE PF;
(3)解法一:作直径AH,连接BH
∴∠ABH=90°,
∵BT切⊙O于点B,
∴∠EBA=∠AHB
∵cos∠EBA=,
∴cos∠AHB=,
∵sin2∠AHB+cos2∠AHB=1,又∠AHB为锐角,
∴sin∠AHB=.
在Rt△ABH中,
∵sin∠AHB=,AB=4,
∴AH==6,
∴⊙O半径为3;
解法二:作直径BH,连接AH(如图).
∴∠BAH=90°,
∵BT切⊙O于点B,
∴∠EBH=90°,
∵cos∠EBA=,
∴sin∠ABH==,
设AH=x,则BH=3x,
在Rt△ABH中,AB=4,
由勾股定理,AB2+AH2=BH2,
∴(4)2+x2=(3x)2
解得x1=2,x2=﹣2(负值舍去)
∴BH=6,
∴⊙O半径为3.
3.解:(1)作BH⊥AC于H,如图,
设AH=x,则CH=6﹣x,
在Rt△ABH中,BH2+x2=52,
在Rt△CBH中,BH2+(6﹣x)2=72,
解得x=1,BH=2,
在Rt△ABH中,sinA==;
在Rt△CBH中,sinC==;
即sinA=,sinC=;
(2)作DE⊥AB于E,DF⊥BC于F,如图,设⊙D的半径为r,
∵⊙D与边AB、BC都相切,
∴DE=DF=r,
在Rt△ADE中,sinA==,
∴DA=r,
在Rt△CDF中,sinC==,
∴DC=r,
∵DA+DC=AC,
∴r+r=6,
解得r=,
即⊙D的半径为.
4.(1)解:∵直线l与以BC为直径的圆O相切于点C.
∴∠BCE=90°,
又∵BC为直径,
∴∠BFC=∠CFE=90°,
∵∠FEC=∠CEB,
∴△CEF∽△BEC,
∴,
∵BE=15,CE=9,
即:,
解得:EF=;
(2)证明:①∵∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,
∴∠ABF=∠FCD,
同理:∠AFB=∠CFD,
∴△CDF∽△BAF;
②∵△CDF∽△BAF,
∴,
又∵∠FCE=∠CBF,∠BFC=∠CFE=90°,
∴△CEF∽△BCF,
∴,
∴,
又∵AB=BC,
∴CE=CD;
(3)解:∵CE=CD,
∴BC=CD=CE,
在Rt△BCE中,tan∠CBE=,
∴∠CBE=30°,
故为60°,
∴F在直径BC下方的圆弧上,且=.
5.(1)证明:如图1,连接FO并延长交⊙O于Q,连接DQ.
∵FQ是⊙O直径,
∴∠FDQ=90°.
∴∠QFD+∠Q=90°.
∵CD⊥AB,
∴∠P+∠C=90°.
∵∠Q=∠C,
∴∠QFD=∠P.
∵∠FOE=∠POF,
∴△FOE∽△POF.
∴,
∴OE OP=OF2=r2.
(2)解:(1)中的结论成立.
理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
∵FM是⊙O直径,
∴∠FCM=90°,
∴∠M+∠CFM=90°.
∵CD⊥AB,
∴∠E+∠D=90°.
∵∠M=∠D,
∴∠CFM=∠E.
∵∠POF=∠FOE,
∴△POF∽△FOE.
∴,
∴OE OP=OF2=r2.
6.(1)证明:连接OE.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°;
在△BOE中,OB=OE,∠B=60°,
∴∠B=∠OEB=∠BOE=60°,
∴∠BOE=∠A=60°,
∴OE∥AC(同位角相等,两直线平行);
∵EF⊥AC,
∴OE⊥EF,即直线EF是⊙O的切线;
(2)解:连接DF.
∵DF与⊙O相切,
∴∠ADF=90°.
设⊙O的半径是r,则EB=r,EC=4﹣r,AD=4﹣2r.
在Rt△ADF中,∠A=60°,
∴AF=2AD=8﹣4r.
∴FC=4r﹣4;
在Rt△CEF中,∵∠C=60°,∴EC=2FC,
∴4﹣r=2(4r﹣4),
解得,r=;
∴⊙O的半径是.
7.(1)解:连接OE.
∵DE垂直平分半径OA,
∴OC=OA
∵OA=OE,
∴OC=OE,CE=DE=,
∴∠OEC=30°,
∴OE==;
(2)证明:由(1)知:∠AOE=60°,,
∴∠B=∠AOE=30°,
∴∠BDE=60°
∵BD∥ME,
∴∠MED=∠BDE=60°,
∴∠MEO=∠MED+∠OEC=60°+30°=90°,
∴OE⊥EM,
∴EM是⊙O的切线;
(3)解:连接OF.
∵∠DPA=45°,
∵∠DCB=90°,
∴∠CDP=45°,
∴∠EOF=2∠EDF=90°,
∴S阴影=S扇形EOF﹣S△EOF==π﹣.
8.(1)证明:∵AB为直径,
∴∠ACB=90°,即:AC⊥BC,
又OE⊥BC,
∴OE∥AC,
∴∠BAC=∠FOB,
∵BN是半圆的切线,
∴∠BCA=∠FBO=90°,
∴△ABC∽△OFB.
(2)解:连接OP,
由△ACB∽△OBF得,∠OFB=∠DBA,∠BCA=∠FBO=90°,
∵AM、BN是⊙O的切线,
∴∠DAB=∠OBF=90°,
∴△ABD∽△BFO,
∴当△ABD与△BFO的面积相等时,△ABD≌△BFO,
∴AD=OB=1,
∵DP切圆O,DA切圆O,
∴DP=DA,
∵△ABD≌△BFO,
∴DA=BO=PO=DP,
又∵∠DAO=∠DPO=90°,
∴四边形AOPD是正方形,
∴DQ∥AB,
∴四边形ABQD是矩形,
∴BQ=AD=1;
(3)证明:由(2)知,△ABD∽△BFO,
∴=,
∴BF===,
∵DP是半圆O的切线,射线AM、BN为半圆O的切线,
∴AD=DP,QB=QP,
过Q点作AM的垂线QK,垂足为K,在Rt△DQK中,
DQ2=QK2+DK2,
∴(AD+BQ)2=(AD﹣BQ)2+22.
∴BQ=,
∴BF=2BQ,
∴Q为BF的中点.
9.解:(1)过点O作OE⊥AB于E,
则AE=BE=AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴BE=OB cos∠B=2×=,
∴AB=2;
故答案为:2;
(2)连接OA,
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°;
(3)∵∠BCO=∠A+∠D,
∴∠BCO>∠A,∠BCO>∠D,
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°,
此时∠BOC=60°,∠BOD=120°,
∴∠DAC=60°,
∴△DAC∽△BOC,
∵∠BCO=90°,
即OC⊥AB,
∴AC=AB=.
∴当AC的长度为时,以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似.
10.解:(1)取BP的中点E,连接QE;
∵Q是PC的中点,E是PB的中点,
∴QE为△PBC的中位线,QE∥BC;
∵AT为经过A点的切线,AB为直径,
∴AT⊥AB,
∵CD⊥AB,
∴AT∥CD,∠TAO=∠QPE=90°,
∴△BPQ∽△BAT,
∴;
∵PB=2PE,AB=2AO,
∴,
∴△TAO∽△QPE,
∴∠AOT=∠PEQ,
∴OT∥QE;
∵QE∥BC,
∴BC∥OT.
(2)∠AOT=∠CBP;
∵CD⊥AB,AB为直径CD=8,
∴CP=PD=4;
连接OC,在Rt△OCP中,
∵PC=4,OC=AB=5,
∴OP=3,
∴PB=OB﹣OP=2,
∴△ATO∽△CPB,
∴;
∵AO=AB=5,
∴AT=10.
(3)在Rt△OAT中,OT==5,
∵AT∥CR,
∴△AOT∽△POR,
∴,
OR=,
∴TR=OT+OR=8.
11.证明:(1)连接DE,
∵∠ABC=90°,
∴∠ABE=90°,
∴AE是⊙O直径
∴∠ADE=90°,即DE⊥AC,
又∵D是AC的中点,
∴DE是AC的垂直平分线,
∴AE=CE;
(2)在△ADE和△EFA中,
∵∠ADE=∠AEF=90°,∠DAE=∠EAF,
∴△ADE∽△AEF,
∴=,即=,
解得:AE=2cm;
即⊙O的直径为2cm,
∴⊙O的半径为cm;
∵∠ADE=∠FDE=∠AEF=90°,
∴∠DAE+∠AED=∠FED+∠AED=90°,
∴∠DAE=∠DEF,
∴△ADE∽△EDF,
∴=,
∴DE2=AD DF=2×4=8,
∴DE=2,
在Rt△CDE中,CE==2,
∴sin∠CED=,
∵∠CAB=∠CED,
∴sin∠CAB=;
(3)∵AE=CE,
∴∠DAE=∠ACB,
∵∠CAB+∠ACB=90°,∠DEA+∠DAE=90°,
∴∠CAB=∠DEA,
∵CF=k CD,点D是AC中点,
∴DF=(k+1)CD,
∵△ADE∽△EDF,
∴=,
∴DE2=AD DF=(k+1)CD2,
∴DE=CD,
在Rt△CDE中,CE==CD,
∴sin∠CED===,
∵∠CAB=∠CED,
∴sin∠CAB=.
12.解:(1)当P是OA的中点时,PB=3,
∵CE是⊙O的切线,
∴AB⊥CE,
又∵CP⊥PE,∠CPB=∠E,
∴△CBP∽△PBE,
∴=,
∴BE=,
∴在Rt△PBE中,PE===;
(2)在Rt△PDG中,由∠PDF=∠E=∠CPB,可知∠GPF=∠GFP
于是GD=GP=GF,
直径AB平分弦DF,有两种可能:
(ⅰ)弦DF不是直径,如图1,则AB⊥DF,于是PD=PF,∠GPD=∠GDP=45°
∴BP=BC=2=BO,点P与点O重合.S△PDF=×2×2=2;
(ⅱ)弦DF恰为直径,如图2,
则点P即为点A.而BC=2,BP=4,
∴BE=8,
S△PCE=×10×4=20,
∴S△PDF=()2×20=.
13.(1)证明:连接CB,AB,CE,
∵点C为劣弧AB上的中点,
∴CB=CA,
又∵CD=CA,
∴AC=CD=BC,
∴∠D=∠CBD,∠CAB=∠CBA,
∴2∠CBD+2∠CBA=180°,
∴∠CBD+∠CBA=90°,
∴∠ABD=90°,
∴∠ABE=90°,
即弧AE的度数是180°,
∴AE是⊙O的直径;
(2)解:∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=10,AC=4,
∴根据勾股定理得:CE=2,
∴S阴影=S半圆﹣S△ACE=12.5π﹣×4×2=12.5π﹣4.
14.证明:(1)连接OD,
∵DE是⊙O的切线,
∴OD⊥DE,
∵DE∥BC,
∴OD⊥BC,
∴弧BD=弧CD,
∴∠BAD=∠EAD
∵∠BDA=∠BCA,DE∥BC,
∴∠BDA=∠DEA,
∵∠BAD=∠EAD,
∴△ABD∽△ADE;
(2)由(1)得,
即AD2=AB AE,
设在△ABE中,AE边上的高为h,则S△ABE=h AE,
∵△ABC为锐角三角形,
∴h<AB,
由∠ABC=45°,AD⊥AF可推得△ADF为等腰直角三角形,
∴S△ADF=×AD×AF=AD2
∴AD2=AE×AB.
∵h<AB.
∴S△DAF>S△BAE.
15.(1)证明:连接OE,如图所示:
则OE=OB,
∴∠OEB=∠OBE,
∵BE平分∠ABC,
∴∠0BE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠ADB,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
∴∠AEO=90°,
∴OE⊥AD,
∴AD与⊙O相切;
(2)解:∵AB=AC,AD平分∠BAC,
∴BD=BC,∠ABC=∠C,
∵BC=4,cosC=,
∴BD=2,cos∠ABC=,
在Rt△ABD中,AB==6,
设⊙O的半径为r,则OA=6﹣r,
∵OE∥BC,
∴△AOE∽△ABD,
∴,
即,
解得:r=,
∴⊙O的半径为.
16.(1)证明:∵AB为⊙O的直径,
∴∠BCA=90°,
∵PC为⊙O的切线,
∴∠BCD=∠BAC,
∵BD⊥PD,
∴∠BDP=∠BCA=90,
∴Rt△BDC∽Rt△BCA,
∴,
∴BC2=BD BA.
(2)解:∵Rt△BDC∽Rt△BCA,
∴∠DBC=∠CBA,
∴EC=AC,
∴EC=AC=6,
∵∠DBC=∠CBA,
∴∠DCE=∠CBA,
∴Rt△CED∽Rt△BAC,
∴,
∴AB=9,
由勾股定理得,
∵∠PCA=∠PBC,∠P=∠P,
∴△PCA∽△PBC,
∴,
设PA=6m,则PC=m,
由切割线定理得PC2=PA PB,
∴45m2=6m(6m+9),
解得m=6,
∴PC=.
17.(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠ADE+∠EDB=∠ABD+∠EDB=90°,
∴∠ADE=∠ABD=∠DAP,
∴PD=PA,
∵∠DFA+∠DAC=∠ADE+∠PDF=90°,且∠ADB=90°,
∴∠PDF=∠PFD,
∴PD=PF,
∴PA=PF,
即:P是AF的中点;
(3)解:∵∠DAF=∠DBA,∠ADB=∠FDA=90°,
∴△FDA∽△ADB,
∴=,
由题意可知圆的半径为5,
∴AB=10,
∴===,
∴在Rt△ABD中,tan∠ABD==,
即:tan∠ABF=.
18.(1)证明:如图,连接OE,
∵DE∥OA,
∴∠COA=∠ODE,∠EOA=∠OED,
∵OD=OE,
∴∠ODE=∠OED,
∴∠COA=∠EOA,
又∵OC=OE,OA=OA,
∴△OAC≌△OAE(SAS),
∴∠OEA=∠OCA=90°,
∴OE⊥AB,
∴直线AB是⊙O的切线;
(2)解:由(1)知△OAC≌△OAE,
∴AE=AC=1,AB=1+2=3,
在直角△ABC中,,
∵∠B=∠B,∠BCA=∠BEO,
∴△BOE∽△BAC,
∴,
∴在直角△AOC中,tan∠OAC=.
19.(1)证明:∵AC是⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
∵OD∥BC,
∴AE⊥OD,
∴D是的中点;
(2)证明:
方法一:
如图,延长OD交AB于G,则OG∥BC,
∴∠AGD=∠B,
∵∠ADO=∠BAD+∠AGD,
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠DAO=∠B+∠BAD;
方法二:
如图,延长AD交BC于H,
则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠DAO=∠B+∠BAD;
(3)解:∵AO=OC,
∴S△OCD=S△ACD,
∵,
∴,
∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴,
即:,
∴CF=2.
20.(1)解:过D作DF⊥BC于F,
∵AD∥BC,∠ABC=90°,
∴AD和BC为⊙O的切线,
而CD为⊙O的切线,
∴DE=DA=x,CE=CB=y,
而DF=AB=8,FC=y﹣x,
∴(x+y)2=82+(x﹣y)2,
∴y=;
(2)证明:连AE,
∵AB为直径,
∴∠AEB=90°,
而DA=DE,
∴∠DAE=∠DEA,
而∠DAE+∠F=∠DEA+∠DEF=90°,
∴∠F=∠DEF,
∴DE=DF,
∴AD=AF;
(3)解:当0<t≤2,
∵DQ=t,BP=t,
∴当AQ=BP时,∠MQD=90°,
∴t+t=2,
∴t=1;
当2<t≤8,
若∠QDM=90°,如图,
∴∠AQD=∠C,
∴Rt△AQD∽Rt△PCM,
∴AD:PM=AQ:PC,即AD:AQ=PM:PC,
而PM:PC=DF:FC=8:6=4:3,
∵AQ=t﹣2,
∴2:(t﹣2)=4:3,
∴t=;
若∠QMD=90°,如图,
过M作MH⊥AB,
∴∠HQM=∠C,
∴Rt△HQM∽Rt△PCM,
∴MH:MP=HQ:PC,即HM:HQ=MP:PC,
∴HM:HQ=MP:PC=DF:FC=4:3,
PC=8﹣t,PM=(8﹣t),
而MH=t,QH=BH﹣BQ=(8﹣t)﹣(10﹣t)=﹣t,
∴t:(﹣t)=4:3,
∴t=<2,舍去.
当∠DQM=90°,如图,
过M作MH⊥AB于H点,则PM=(8﹣t),MN=t,AQ=t﹣2,
∴QH=8﹣(t﹣2)﹣(8﹣t)=t﹣,
∴Rt△AQD∽Rt△HMQ,
∴AD:QH=AQ:HM,即2:(t﹣)=(t﹣2):t,
∴t2﹣10t+4=0,t=5±,
∴t=5+>8(舍).
1.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
2.已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过点P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)当点P在线段AB上时(如图).求证:PA PB=PE PF;
(2)当点P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明;如果不成立,请说明理由;
(3)若,,求⊙O的半径.
3.如图,在△ABC中,AB=5,AC=6,BC=7.
(1)求sinA和sinC的值;
(2)若⊙D的圆心D在边AC上,且⊙D与边AB、BC都相切,求⊙D的半径.
4.如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC于点D.
(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使BC=CD,请说明你的理由.
5.已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、O、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE OP=r2;
(2)当点E在AB(或BA)的延长线上时,以图2点E的位置为例,(1)中的结论是否成立?请说明理由.
6.已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
7.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连接BD,过点E作EM∥BD,交BA的延长线于点M.
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.
8.如图,AB是半圆O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO面积相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.
9.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB等于 (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似?请写出解答过程.
10.如图,在圆O中AB是直径,AT是经过点A的切线,弦CD垂直AB于P点,线段CP的中点为Q,连接BQ并延长交切线AT于T点,连接OT.
(1)求证:BC∥OT;
(2)若⊙O直径为10,CD=8,求AT的长;
(3)延长TO交直线CD于R,若⊙O直径为10,CD=8,求TR的长.
11.如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E,过点E作⊙O的切线,交AC的延长线于点F.
(1)求证:AE=CE;
(2)若CF=CD=2,求⊙O的半径和sin∠CAB的值;
(3)若CF=k CD(k>0),直接写出sin∠CAB的值(用含k的代数式表示).
12.如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA上一动点,连接PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连接DF交AB于点G.
(1)当P是OA的中点时,求PE的长;
(2)若∠PDF=∠E,求△PDF的面积.
13.如图1,已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,连接DB并延长DB交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图2,连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和.(结果保留π与根号)
14.已知:如图,锐角三角形ABC内接于⊙O,∠ABC=45°;点D是上的一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连接AD、BD、BE,AD的垂线AF与DC的延长线交于点F.
(1)求证:△ABD∽△ADE;
(2)记△DAF、△BAE的面积分别为S△DAF、S△BAE,求证:S△DAF>S△BAE.
15.已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E,F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC=,求⊙O的半径.
16.已知:如图,AB是⊙O的直径,点P为BA延长线上一点,PC为⊙O的切线,C为切点,BD⊥PC,垂足为D,交⊙O于E,连接AC、BC、EC.
(1)求证:BC2=BD BA;
(2)若AC=6,DE=4,求PC的长.
17.已知:如图.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)若⊙O的半径为5,AF=,求tan∠ABF的值.
18.如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B.
(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2,求tan∠OAC的值.
19.如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
(1)求证:D是的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若,且AC=4,求CF的长.
20.如图1,梯形ABCD中,AD∥BC,AB=8,∠ABC=90°,以AB为直径的⊙O切CD于点E.
(1)若设AD=x,BC=y,试求出y与x之间的函数关系式;
(2)如图2,BE的延长线交AD的延长线于点F.求证:AD=AF;
(3)如图3,若AD=2,BC=8.动点P以每秒1个单位长的速度,从点B沿线段BC向点C运动;同时点Q以相同的速度,从点D沿折线D﹣A﹣B向点B运动.当点P到达点C时,两点同时停止运动.过点P作直线PM⊥BC与折线B﹣D﹣C的交点为M.点P运动的时间为t(秒).点P在线段BC上运动时,是否可以使得以D、M、Q为顶点的三角形为直角三角形,若可以,请求出t的值;若不可以,请说明理由.
参考答案
1.(1)证明:连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴PB∥OC,
∵CD⊥PA,
∴CD⊥OC,CO为⊙O半径,
∴CD为⊙O的切线;
(2)解:过O作OF⊥AB,垂足为F,
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形DCOF为矩形,
∴OC=FD,OF=CD.
∵DC+DA=6,
设AD=x,则OF=CD=6﹣x,
∵⊙O的直径为10,
∴DF=OC=5,
∴AF=5﹣x,
在Rt△AOF中,由勾股定理得AF2+OF2=OA2.
即(5﹣x)2+(6﹣x)2=25,
化简得x2﹣11x+18=0,
解得x1=2,x2=9.
∵CD=6﹣x大于0,故x=9舍去,
∴x=2,
从而AD=2,AF=5﹣2=3,
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴AB=2AF=6.
2.(1)证明:∵BT切⊙O于点B,
∴∠EBA=∠C,
∵EF∥BC,
∴∠AFP=∠C,
∠AFP=∠EBP,
∵∠APF=∠EPB,
∴△PFA∽△PBE,
∴,
∴PA PB=PE PF;
(2)解:当P为BA延长线上一点时,第(1)题的结论仍成立(如图)
∵BT切⊙O于点B,
∴∠EBA=∠C,
∵EF∥BC,
∴∠PFA=∠C,
∠PFA=∠PBE,
又∵∠APF=∠EPB,
∴△PFA∽△PBE,
∴,
∴PA PB=PE PF;
(3)解法一:作直径AH,连接BH
∴∠ABH=90°,
∵BT切⊙O于点B,
∴∠EBA=∠AHB
∵cos∠EBA=,
∴cos∠AHB=,
∵sin2∠AHB+cos2∠AHB=1,又∠AHB为锐角,
∴sin∠AHB=.
在Rt△ABH中,
∵sin∠AHB=,AB=4,
∴AH==6,
∴⊙O半径为3;
解法二:作直径BH,连接AH(如图).
∴∠BAH=90°,
∵BT切⊙O于点B,
∴∠EBH=90°,
∵cos∠EBA=,
∴sin∠ABH==,
设AH=x,则BH=3x,
在Rt△ABH中,AB=4,
由勾股定理,AB2+AH2=BH2,
∴(4)2+x2=(3x)2
解得x1=2,x2=﹣2(负值舍去)
∴BH=6,
∴⊙O半径为3.
3.解:(1)作BH⊥AC于H,如图,
设AH=x,则CH=6﹣x,
在Rt△ABH中,BH2+x2=52,
在Rt△CBH中,BH2+(6﹣x)2=72,
解得x=1,BH=2,
在Rt△ABH中,sinA==;
在Rt△CBH中,sinC==;
即sinA=,sinC=;
(2)作DE⊥AB于E,DF⊥BC于F,如图,设⊙D的半径为r,
∵⊙D与边AB、BC都相切,
∴DE=DF=r,
在Rt△ADE中,sinA==,
∴DA=r,
在Rt△CDF中,sinC==,
∴DC=r,
∵DA+DC=AC,
∴r+r=6,
解得r=,
即⊙D的半径为.
4.(1)解:∵直线l与以BC为直径的圆O相切于点C.
∴∠BCE=90°,
又∵BC为直径,
∴∠BFC=∠CFE=90°,
∵∠FEC=∠CEB,
∴△CEF∽△BEC,
∴,
∵BE=15,CE=9,
即:,
解得:EF=;
(2)证明:①∵∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,
∴∠ABF=∠FCD,
同理:∠AFB=∠CFD,
∴△CDF∽△BAF;
②∵△CDF∽△BAF,
∴,
又∵∠FCE=∠CBF,∠BFC=∠CFE=90°,
∴△CEF∽△BCF,
∴,
∴,
又∵AB=BC,
∴CE=CD;
(3)解:∵CE=CD,
∴BC=CD=CE,
在Rt△BCE中,tan∠CBE=,
∴∠CBE=30°,
故为60°,
∴F在直径BC下方的圆弧上,且=.
5.(1)证明:如图1,连接FO并延长交⊙O于Q,连接DQ.
∵FQ是⊙O直径,
∴∠FDQ=90°.
∴∠QFD+∠Q=90°.
∵CD⊥AB,
∴∠P+∠C=90°.
∵∠Q=∠C,
∴∠QFD=∠P.
∵∠FOE=∠POF,
∴△FOE∽△POF.
∴,
∴OE OP=OF2=r2.
(2)解:(1)中的结论成立.
理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
∵FM是⊙O直径,
∴∠FCM=90°,
∴∠M+∠CFM=90°.
∵CD⊥AB,
∴∠E+∠D=90°.
∵∠M=∠D,
∴∠CFM=∠E.
∵∠POF=∠FOE,
∴△POF∽△FOE.
∴,
∴OE OP=OF2=r2.
6.(1)证明:连接OE.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°;
在△BOE中,OB=OE,∠B=60°,
∴∠B=∠OEB=∠BOE=60°,
∴∠BOE=∠A=60°,
∴OE∥AC(同位角相等,两直线平行);
∵EF⊥AC,
∴OE⊥EF,即直线EF是⊙O的切线;
(2)解:连接DF.
∵DF与⊙O相切,
∴∠ADF=90°.
设⊙O的半径是r,则EB=r,EC=4﹣r,AD=4﹣2r.
在Rt△ADF中,∠A=60°,
∴AF=2AD=8﹣4r.
∴FC=4r﹣4;
在Rt△CEF中,∵∠C=60°,∴EC=2FC,
∴4﹣r=2(4r﹣4),
解得,r=;
∴⊙O的半径是.
7.(1)解:连接OE.
∵DE垂直平分半径OA,
∴OC=OA
∵OA=OE,
∴OC=OE,CE=DE=,
∴∠OEC=30°,
∴OE==;
(2)证明:由(1)知:∠AOE=60°,,
∴∠B=∠AOE=30°,
∴∠BDE=60°
∵BD∥ME,
∴∠MED=∠BDE=60°,
∴∠MEO=∠MED+∠OEC=60°+30°=90°,
∴OE⊥EM,
∴EM是⊙O的切线;
(3)解:连接OF.
∵∠DPA=45°,
∵∠DCB=90°,
∴∠CDP=45°,
∴∠EOF=2∠EDF=90°,
∴S阴影=S扇形EOF﹣S△EOF==π﹣.
8.(1)证明:∵AB为直径,
∴∠ACB=90°,即:AC⊥BC,
又OE⊥BC,
∴OE∥AC,
∴∠BAC=∠FOB,
∵BN是半圆的切线,
∴∠BCA=∠FBO=90°,
∴△ABC∽△OFB.
(2)解:连接OP,
由△ACB∽△OBF得,∠OFB=∠DBA,∠BCA=∠FBO=90°,
∵AM、BN是⊙O的切线,
∴∠DAB=∠OBF=90°,
∴△ABD∽△BFO,
∴当△ABD与△BFO的面积相等时,△ABD≌△BFO,
∴AD=OB=1,
∵DP切圆O,DA切圆O,
∴DP=DA,
∵△ABD≌△BFO,
∴DA=BO=PO=DP,
又∵∠DAO=∠DPO=90°,
∴四边形AOPD是正方形,
∴DQ∥AB,
∴四边形ABQD是矩形,
∴BQ=AD=1;
(3)证明:由(2)知,△ABD∽△BFO,
∴=,
∴BF===,
∵DP是半圆O的切线,射线AM、BN为半圆O的切线,
∴AD=DP,QB=QP,
过Q点作AM的垂线QK,垂足为K,在Rt△DQK中,
DQ2=QK2+DK2,
∴(AD+BQ)2=(AD﹣BQ)2+22.
∴BQ=,
∴BF=2BQ,
∴Q为BF的中点.
9.解:(1)过点O作OE⊥AB于E,
则AE=BE=AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴BE=OB cos∠B=2×=,
∴AB=2;
故答案为:2;
(2)连接OA,
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°;
(3)∵∠BCO=∠A+∠D,
∴∠BCO>∠A,∠BCO>∠D,
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°,
此时∠BOC=60°,∠BOD=120°,
∴∠DAC=60°,
∴△DAC∽△BOC,
∵∠BCO=90°,
即OC⊥AB,
∴AC=AB=.
∴当AC的长度为时,以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似.
10.解:(1)取BP的中点E,连接QE;
∵Q是PC的中点,E是PB的中点,
∴QE为△PBC的中位线,QE∥BC;
∵AT为经过A点的切线,AB为直径,
∴AT⊥AB,
∵CD⊥AB,
∴AT∥CD,∠TAO=∠QPE=90°,
∴△BPQ∽△BAT,
∴;
∵PB=2PE,AB=2AO,
∴,
∴△TAO∽△QPE,
∴∠AOT=∠PEQ,
∴OT∥QE;
∵QE∥BC,
∴BC∥OT.
(2)∠AOT=∠CBP;
∵CD⊥AB,AB为直径CD=8,
∴CP=PD=4;
连接OC,在Rt△OCP中,
∵PC=4,OC=AB=5,
∴OP=3,
∴PB=OB﹣OP=2,
∴△ATO∽△CPB,
∴;
∵AO=AB=5,
∴AT=10.
(3)在Rt△OAT中,OT==5,
∵AT∥CR,
∴△AOT∽△POR,
∴,
OR=,
∴TR=OT+OR=8.
11.证明:(1)连接DE,
∵∠ABC=90°,
∴∠ABE=90°,
∴AE是⊙O直径
∴∠ADE=90°,即DE⊥AC,
又∵D是AC的中点,
∴DE是AC的垂直平分线,
∴AE=CE;
(2)在△ADE和△EFA中,
∵∠ADE=∠AEF=90°,∠DAE=∠EAF,
∴△ADE∽△AEF,
∴=,即=,
解得:AE=2cm;
即⊙O的直径为2cm,
∴⊙O的半径为cm;
∵∠ADE=∠FDE=∠AEF=90°,
∴∠DAE+∠AED=∠FED+∠AED=90°,
∴∠DAE=∠DEF,
∴△ADE∽△EDF,
∴=,
∴DE2=AD DF=2×4=8,
∴DE=2,
在Rt△CDE中,CE==2,
∴sin∠CED=,
∵∠CAB=∠CED,
∴sin∠CAB=;
(3)∵AE=CE,
∴∠DAE=∠ACB,
∵∠CAB+∠ACB=90°,∠DEA+∠DAE=90°,
∴∠CAB=∠DEA,
∵CF=k CD,点D是AC中点,
∴DF=(k+1)CD,
∵△ADE∽△EDF,
∴=,
∴DE2=AD DF=(k+1)CD2,
∴DE=CD,
在Rt△CDE中,CE==CD,
∴sin∠CED===,
∵∠CAB=∠CED,
∴sin∠CAB=.
12.解:(1)当P是OA的中点时,PB=3,
∵CE是⊙O的切线,
∴AB⊥CE,
又∵CP⊥PE,∠CPB=∠E,
∴△CBP∽△PBE,
∴=,
∴BE=,
∴在Rt△PBE中,PE===;
(2)在Rt△PDG中,由∠PDF=∠E=∠CPB,可知∠GPF=∠GFP
于是GD=GP=GF,
直径AB平分弦DF,有两种可能:
(ⅰ)弦DF不是直径,如图1,则AB⊥DF,于是PD=PF,∠GPD=∠GDP=45°
∴BP=BC=2=BO,点P与点O重合.S△PDF=×2×2=2;
(ⅱ)弦DF恰为直径,如图2,
则点P即为点A.而BC=2,BP=4,
∴BE=8,
S△PCE=×10×4=20,
∴S△PDF=()2×20=.
13.(1)证明:连接CB,AB,CE,
∵点C为劣弧AB上的中点,
∴CB=CA,
又∵CD=CA,
∴AC=CD=BC,
∴∠D=∠CBD,∠CAB=∠CBA,
∴2∠CBD+2∠CBA=180°,
∴∠CBD+∠CBA=90°,
∴∠ABD=90°,
∴∠ABE=90°,
即弧AE的度数是180°,
∴AE是⊙O的直径;
(2)解:∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=10,AC=4,
∴根据勾股定理得:CE=2,
∴S阴影=S半圆﹣S△ACE=12.5π﹣×4×2=12.5π﹣4.
14.证明:(1)连接OD,
∵DE是⊙O的切线,
∴OD⊥DE,
∵DE∥BC,
∴OD⊥BC,
∴弧BD=弧CD,
∴∠BAD=∠EAD
∵∠BDA=∠BCA,DE∥BC,
∴∠BDA=∠DEA,
∵∠BAD=∠EAD,
∴△ABD∽△ADE;
(2)由(1)得,
即AD2=AB AE,
设在△ABE中,AE边上的高为h,则S△ABE=h AE,
∵△ABC为锐角三角形,
∴h<AB,
由∠ABC=45°,AD⊥AF可推得△ADF为等腰直角三角形,
∴S△ADF=×AD×AF=AD2
∴AD2=AE×AB.
∵h<AB.
∴S△DAF>S△BAE.
15.(1)证明:连接OE,如图所示:
则OE=OB,
∴∠OEB=∠OBE,
∵BE平分∠ABC,
∴∠0BE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠ADB,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
∴∠AEO=90°,
∴OE⊥AD,
∴AD与⊙O相切;
(2)解:∵AB=AC,AD平分∠BAC,
∴BD=BC,∠ABC=∠C,
∵BC=4,cosC=,
∴BD=2,cos∠ABC=,
在Rt△ABD中,AB==6,
设⊙O的半径为r,则OA=6﹣r,
∵OE∥BC,
∴△AOE∽△ABD,
∴,
即,
解得:r=,
∴⊙O的半径为.
16.(1)证明:∵AB为⊙O的直径,
∴∠BCA=90°,
∵PC为⊙O的切线,
∴∠BCD=∠BAC,
∵BD⊥PD,
∴∠BDP=∠BCA=90,
∴Rt△BDC∽Rt△BCA,
∴,
∴BC2=BD BA.
(2)解:∵Rt△BDC∽Rt△BCA,
∴∠DBC=∠CBA,
∴EC=AC,
∴EC=AC=6,
∵∠DBC=∠CBA,
∴∠DCE=∠CBA,
∴Rt△CED∽Rt△BAC,
∴,
∴AB=9,
由勾股定理得,
∵∠PCA=∠PBC,∠P=∠P,
∴△PCA∽△PBC,
∴,
设PA=6m,则PC=m,
由切割线定理得PC2=PA PB,
∴45m2=6m(6m+9),
解得m=6,
∴PC=.
17.(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠ADE+∠EDB=∠ABD+∠EDB=90°,
∴∠ADE=∠ABD=∠DAP,
∴PD=PA,
∵∠DFA+∠DAC=∠ADE+∠PDF=90°,且∠ADB=90°,
∴∠PDF=∠PFD,
∴PD=PF,
∴PA=PF,
即:P是AF的中点;
(3)解:∵∠DAF=∠DBA,∠ADB=∠FDA=90°,
∴△FDA∽△ADB,
∴=,
由题意可知圆的半径为5,
∴AB=10,
∴===,
∴在Rt△ABD中,tan∠ABD==,
即:tan∠ABF=.
18.(1)证明:如图,连接OE,
∵DE∥OA,
∴∠COA=∠ODE,∠EOA=∠OED,
∵OD=OE,
∴∠ODE=∠OED,
∴∠COA=∠EOA,
又∵OC=OE,OA=OA,
∴△OAC≌△OAE(SAS),
∴∠OEA=∠OCA=90°,
∴OE⊥AB,
∴直线AB是⊙O的切线;
(2)解:由(1)知△OAC≌△OAE,
∴AE=AC=1,AB=1+2=3,
在直角△ABC中,,
∵∠B=∠B,∠BCA=∠BEO,
∴△BOE∽△BAC,
∴,
∴在直角△AOC中,tan∠OAC=.
19.(1)证明:∵AC是⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
∵OD∥BC,
∴AE⊥OD,
∴D是的中点;
(2)证明:
方法一:
如图,延长OD交AB于G,则OG∥BC,
∴∠AGD=∠B,
∵∠ADO=∠BAD+∠AGD,
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠DAO=∠B+∠BAD;
方法二:
如图,延长AD交BC于H,
则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠DAO=∠B+∠BAD;
(3)解:∵AO=OC,
∴S△OCD=S△ACD,
∵,
∴,
∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴,
即:,
∴CF=2.
20.(1)解:过D作DF⊥BC于F,
∵AD∥BC,∠ABC=90°,
∴AD和BC为⊙O的切线,
而CD为⊙O的切线,
∴DE=DA=x,CE=CB=y,
而DF=AB=8,FC=y﹣x,
∴(x+y)2=82+(x﹣y)2,
∴y=;
(2)证明:连AE,
∵AB为直径,
∴∠AEB=90°,
而DA=DE,
∴∠DAE=∠DEA,
而∠DAE+∠F=∠DEA+∠DEF=90°,
∴∠F=∠DEF,
∴DE=DF,
∴AD=AF;
(3)解:当0<t≤2,
∵DQ=t,BP=t,
∴当AQ=BP时,∠MQD=90°,
∴t+t=2,
∴t=1;
当2<t≤8,
若∠QDM=90°,如图,
∴∠AQD=∠C,
∴Rt△AQD∽Rt△PCM,
∴AD:PM=AQ:PC,即AD:AQ=PM:PC,
而PM:PC=DF:FC=8:6=4:3,
∵AQ=t﹣2,
∴2:(t﹣2)=4:3,
∴t=;
若∠QMD=90°,如图,
过M作MH⊥AB,
∴∠HQM=∠C,
∴Rt△HQM∽Rt△PCM,
∴MH:MP=HQ:PC,即HM:HQ=MP:PC,
∴HM:HQ=MP:PC=DF:FC=4:3,
PC=8﹣t,PM=(8﹣t),
而MH=t,QH=BH﹣BQ=(8﹣t)﹣(10﹣t)=﹣t,
∴t:(﹣t)=4:3,
∴t=<2,舍去.
当∠DQM=90°,如图,
过M作MH⊥AB于H点,则PM=(8﹣t),MN=t,AQ=t﹣2,
∴QH=8﹣(t﹣2)﹣(8﹣t)=t﹣,
∴Rt△AQD∽Rt△HMQ,
∴AD:QH=AQ:HM,即2:(t﹣)=(t﹣2):t,
∴t2﹣10t+4=0,t=5±,
∴t=5+>8(舍).
