人教版数学六年级下册6.5.4整理与复习-有趣的平衡(课件共14张PPT)
文档属性
| 名称 | 人教版数学六年级下册6.5.4整理与复习-有趣的平衡(课件共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 542.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
整理与复习—有趣的平衡
通过实践活动,发现“左边的刻度×左边所放棋子数=右边的刻度×右边所放棋子数”,初步感受杠杆原理。
在实验中发现当“左边的刻度数×左边所放的棋子数”的积不变时,“右边的刻度数”与“右边所放棋子数”成反比例,加深对反比例关系的理解。
经历从特殊到一般的探究过程,培养动手操作及归纳、推理能力,增强应用数学的意识。
1.在相同的刻度处左右两边放相同数量的棋子,竹竿就能平衡。
2.左边刻度数×棋子数=右边刻度数×棋子数。
3.左边刻度数×棋子数的积一定时,右边刻度数与棋子数成反比例。
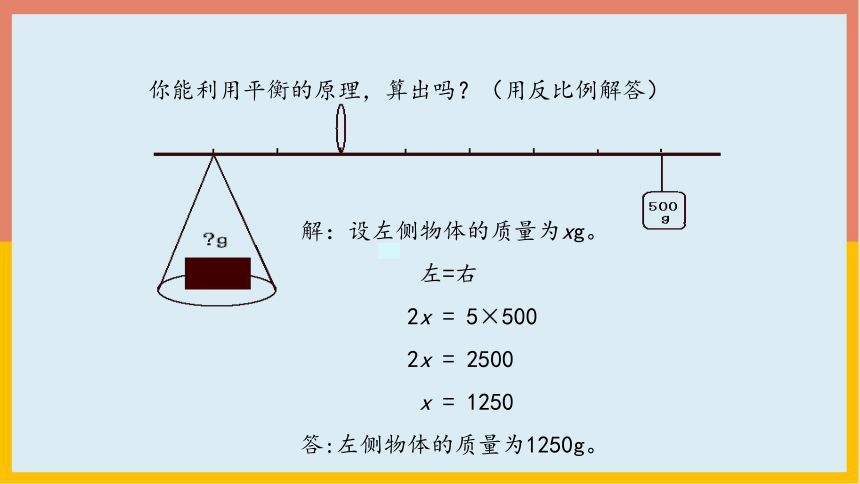
解:设左侧物体的质量为xg。
左=右
2x = 5×500
2x = 2500
x = 1250
答:左侧物体的质量为1250g。
你能利用平衡的原理,算出吗?(用反比例解答)
选一根粗细均匀的竹竿(长约1m),在中点的位置打个小孔并拴上绳子。然后从中点开始每隔8cm做一个记号(可以刻一个小槽)。
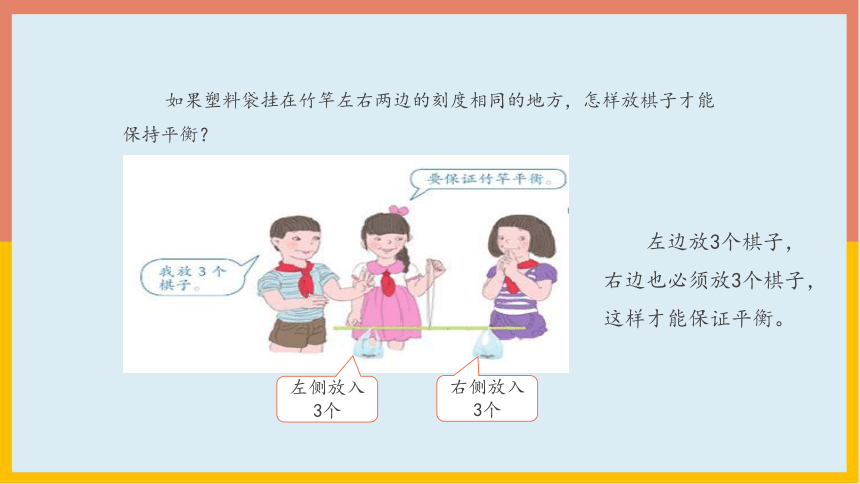
如果塑料袋挂在竹竿左右两边的刻度相同的地方,怎样放棋子才能保持平衡?
左侧放入3个
右侧放入3个
左边放3个棋子,右边也必须放3个棋子,这样才能保证平衡。
如果左右塑料袋放入同样多的棋子(如4个),它们移动到什么位置才能保持平衡?
左侧刻度数是4
右侧刻度数也是4
左边塑料袋挂在刻度“4”的点上,右边塑料袋也要挂在刻度“4”的点上,这样才能保证平衡。
动手做一做,将你的发现填入下表中。
如果左边塑料袋在刻度3上,放4个棋子,右边的塑料袋在刻度4上,放几个才能平衡?
左刻度 3 右刻度 4
所放棋子数 4 所放棋子数
乘积 乘积
3
12
12
动手做一做,将你的发现填入下表中。
如果左边塑料袋在刻度6上,放1个棋子,右边的塑料袋在刻度3上,放几个才能平衡?
左刻度 3 6 右刻度 4 3
所放棋子数 4 1 所放棋子数
乘积 乘积
3
12
12
2
6
6
左边在刻度4上放3个棋子并保持不变,右边分别在各个刻度上放几个棋子才能保证平衡?
右边刻度数增大几倍,棋子数反而减小几倍;刻度数减小几倍,棋子数反而增大几倍。因此,右边的刻度和所放棋子数成反比例关系。
右刻度数 1 2 3 4 6
所放棋子数 12 6 4 3 2
乘积 12 12 12 12 12
母女俩在玩跷跷板,女儿体重12千克,坐的地方距支点15分米,母亲体重60千克,她坐的地方距支点多远才能保持跷跷板的平衡?
解:设她坐的地方距支点的距离是x分米。
60x=12×15
x=3
答:她坐的地方距支点3分米才能保持平衡。
我们生活中玩的跷跷板,用的筷子,剪刀其实都是杠杆原理的运用。阿基米德还说过一句很著名的话:“给我一个支点,我能翘起整个地球。”
有一位菜贩很不老实,他有一架动过手脚的天平。这架天平的两臂不等长。有一天,当他向农民们购买实际重5千克的白菜时,就把白菜放在天平臂较短这一侧,这样称起来较轻,天平显示只有4千克重;而当他把5千克白菜卖出去的时候,他把白菜放在天平臂较长这一侧,这样称起来白菜会比5千克重,你能用所学的知识揭穿他的骗人的伎俩吗?
再见
整理与复习—有趣的平衡
通过实践活动,发现“左边的刻度×左边所放棋子数=右边的刻度×右边所放棋子数”,初步感受杠杆原理。
在实验中发现当“左边的刻度数×左边所放的棋子数”的积不变时,“右边的刻度数”与“右边所放棋子数”成反比例,加深对反比例关系的理解。
经历从特殊到一般的探究过程,培养动手操作及归纳、推理能力,增强应用数学的意识。
1.在相同的刻度处左右两边放相同数量的棋子,竹竿就能平衡。
2.左边刻度数×棋子数=右边刻度数×棋子数。
3.左边刻度数×棋子数的积一定时,右边刻度数与棋子数成反比例。
解:设左侧物体的质量为xg。
左=右
2x = 5×500
2x = 2500
x = 1250
答:左侧物体的质量为1250g。
你能利用平衡的原理,算出吗?(用反比例解答)
选一根粗细均匀的竹竿(长约1m),在中点的位置打个小孔并拴上绳子。然后从中点开始每隔8cm做一个记号(可以刻一个小槽)。
如果塑料袋挂在竹竿左右两边的刻度相同的地方,怎样放棋子才能保持平衡?
左侧放入3个
右侧放入3个
左边放3个棋子,右边也必须放3个棋子,这样才能保证平衡。
如果左右塑料袋放入同样多的棋子(如4个),它们移动到什么位置才能保持平衡?
左侧刻度数是4
右侧刻度数也是4
左边塑料袋挂在刻度“4”的点上,右边塑料袋也要挂在刻度“4”的点上,这样才能保证平衡。
动手做一做,将你的发现填入下表中。
如果左边塑料袋在刻度3上,放4个棋子,右边的塑料袋在刻度4上,放几个才能平衡?
左刻度 3 右刻度 4
所放棋子数 4 所放棋子数
乘积 乘积
3
12
12
动手做一做,将你的发现填入下表中。
如果左边塑料袋在刻度6上,放1个棋子,右边的塑料袋在刻度3上,放几个才能平衡?
左刻度 3 6 右刻度 4 3
所放棋子数 4 1 所放棋子数
乘积 乘积
3
12
12
2
6
6
左边在刻度4上放3个棋子并保持不变,右边分别在各个刻度上放几个棋子才能保证平衡?
右边刻度数增大几倍,棋子数反而减小几倍;刻度数减小几倍,棋子数反而增大几倍。因此,右边的刻度和所放棋子数成反比例关系。
右刻度数 1 2 3 4 6
所放棋子数 12 6 4 3 2
乘积 12 12 12 12 12
母女俩在玩跷跷板,女儿体重12千克,坐的地方距支点15分米,母亲体重60千克,她坐的地方距支点多远才能保持跷跷板的平衡?
解:设她坐的地方距支点的距离是x分米。
60x=12×15
x=3
答:她坐的地方距支点3分米才能保持平衡。
我们生活中玩的跷跷板,用的筷子,剪刀其实都是杠杆原理的运用。阿基米德还说过一句很著名的话:“给我一个支点,我能翘起整个地球。”
有一位菜贩很不老实,他有一架动过手脚的天平。这架天平的两臂不等长。有一天,当他向农民们购买实际重5千克的白菜时,就把白菜放在天平臂较短这一侧,这样称起来较轻,天平显示只有4千克重;而当他把5千克白菜卖出去的时候,他把白菜放在天平臂较长这一侧,这样称起来白菜会比5千克重,你能用所学的知识揭穿他的骗人的伎俩吗?
再见
