人教版数学六年级下册6.4.1整理与复习-探究模式的策略(课件共15张PPT)
文档属性
| 名称 | 人教版数学六年级下册6.4.1整理与复习-探究模式的策略(课件共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 325.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 19:26:29 | ||
图片预览






文档简介
(共15张PPT)
整理与复习-探究模式的策略
通过引导学生观察、列表、分析、归纳,掌握解决“几个点能连成多少条线段”这类问题的方法和规律,并能运用规律解决较复杂的数学问题。
使学生进一步体会“化繁为简”和数形结合的数学思想方法,学会用数学思想方法解决问题,形成一些基本策略,发展实践能力与创新精神。
让学生在体验中感受数学知识的奇妙,感受数学思维的乐趣,在探究中获得成功的愉悦感,激发孩子们进一步学习与探究的欲望。
遇到复杂的问题,你可以怎样思考?
1.化繁为简
2.画图、枚举
3.有序思考
4.探究规律
学校为艺术节选送节目,要从3个合唱节目中选出2个,2个舞蹈节目中选出1个。一共有多少种选送方案?
用A、B、C分别表示3个合唱节目,
用a、b分别表示2个舞蹈节目。
A、B、 a
A、B、 b
B、C 、a
B、C 、b
A、C、 a
A、C、 b
所以,选送的方案共有6种。
唉,画乱了,也数不清多少条线段了。
最多有2个点在同一条直线上,那么6个点可以连多少条线段?8个点呢?
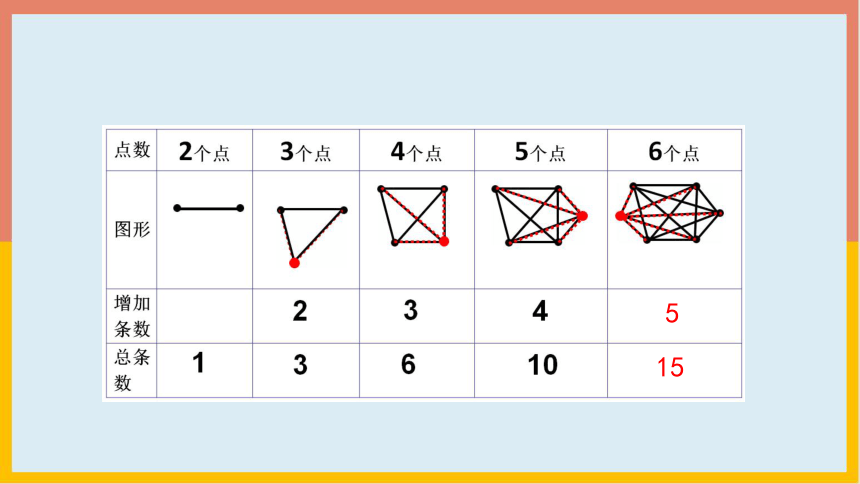
从最少的2个点开始,逐渐增加点数,找找规律吧。
5
15
按照规律,8个点能连几条线段?
1+2+3+4+5+6+7
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
=(1+11)+(2+10)+(3+9)+(4+8)+(5+7)+6
1+2+3+4+5+6+7+8+9+10+11
=66(条) ——12个点
=12×5+6
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19)+(2+18)+(3+17)+……+(8+12)+(9+11)+10
=20×9+10
=190(条) ——20个点
根据规律,你知道12个点、20个点能连多少条线段吗?
n个点:
1+2+3+…+(n-1)
用点连线的规律:
从1开始前(n-1)个连续自然数的和(即从1开始加起,一直加到比点数少1的连续几个自然数的和)。
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
(1)7×7=49(个)
15×15=225(个)
(2)n × n = 棋子总数
n2 =棋子总数
(2)第n幅图有多少个棋子?
2.找规律,填数。
(1)3, 11 , 20 , 30, 53, …
(2)1, 3, 2, 6, 4, 9, 8, , ,15, ,18,…
41
66
12
16
32
3.摆一摆,找规律。
(1)第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
15根
…
(3)摆第n个图形用多少根小棒呢
3+2(n-1)
4.节日期间广场上有一排彩旗,按照1面红旗、2面红旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
55÷(1+2+3)=9组..... 1;
所以,第55面是红旗;
100÷(1+2+3)=16组..... 4;
所以,第100面是绿旗。
复杂问题
化难为易
解决问题
寻找规律
再见
整理与复习-探究模式的策略
通过引导学生观察、列表、分析、归纳,掌握解决“几个点能连成多少条线段”这类问题的方法和规律,并能运用规律解决较复杂的数学问题。
使学生进一步体会“化繁为简”和数形结合的数学思想方法,学会用数学思想方法解决问题,形成一些基本策略,发展实践能力与创新精神。
让学生在体验中感受数学知识的奇妙,感受数学思维的乐趣,在探究中获得成功的愉悦感,激发孩子们进一步学习与探究的欲望。
遇到复杂的问题,你可以怎样思考?
1.化繁为简
2.画图、枚举
3.有序思考
4.探究规律
学校为艺术节选送节目,要从3个合唱节目中选出2个,2个舞蹈节目中选出1个。一共有多少种选送方案?
用A、B、C分别表示3个合唱节目,
用a、b分别表示2个舞蹈节目。
A、B、 a
A、B、 b
B、C 、a
B、C 、b
A、C、 a
A、C、 b
所以,选送的方案共有6种。
唉,画乱了,也数不清多少条线段了。
最多有2个点在同一条直线上,那么6个点可以连多少条线段?8个点呢?
从最少的2个点开始,逐渐增加点数,找找规律吧。
5
15
按照规律,8个点能连几条线段?
1+2+3+4+5+6+7
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
=(1+11)+(2+10)+(3+9)+(4+8)+(5+7)+6
1+2+3+4+5+6+7+8+9+10+11
=66(条) ——12个点
=12×5+6
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19)+(2+18)+(3+17)+……+(8+12)+(9+11)+10
=20×9+10
=190(条) ——20个点
根据规律,你知道12个点、20个点能连多少条线段吗?
n个点:
1+2+3+…+(n-1)
用点连线的规律:
从1开始前(n-1)个连续自然数的和(即从1开始加起,一直加到比点数少1的连续几个自然数的和)。
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
(1)7×7=49(个)
15×15=225(个)
(2)n × n = 棋子总数
n2 =棋子总数
(2)第n幅图有多少个棋子?
2.找规律,填数。
(1)3, 11 , 20 , 30, 53, …
(2)1, 3, 2, 6, 4, 9, 8, , ,15, ,18,…
41
66
12
16
32
3.摆一摆,找规律。
(1)第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
15根
…
(3)摆第n个图形用多少根小棒呢
3+2(n-1)
4.节日期间广场上有一排彩旗,按照1面红旗、2面红旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
55÷(1+2+3)=9组..... 1;
所以,第55面是红旗;
100÷(1+2+3)=16组..... 4;
所以,第100面是绿旗。
复杂问题
化难为易
解决问题
寻找规律
再见
