人教版数学六年级下册6.3.2整理与复习-平均数、中位数和众数(课件共14张PPT)
文档属性
| 名称 | 人教版数学六年级下册6.3.2整理与复习-平均数、中位数和众数(课件共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 110.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
整理与复均数、中位数和众数
1.掌握平均数、中位数、众数的初步知识;
2.进一步理解平均数、中位数、众数这三种统计量的实际意义;
3.养成用数学观点解决实际问题的习惯。
学习目标
平均数、中位数、众数的概念
1.若干个数相加的和,除以这些数的个数所得的结果是这些数的平均数。
2.一组数据,把它们从小到大进行排列。如果有奇数个,那么中间的数就是这种数据的中位数;如果有偶数个,那么中间的两个数的平均数是这组数据的中位数。
3.在一组数中,出现频率最高的数是众数。
知识梳理
平均数: 反映总体平均水平。
中位数:反映中等水平。
众 数:反映多数集中水平。
知识梳理
平均数、中位数和众数的数量和意义
平均数 中位数 众数
数量
意义
一个
一个(奇、偶有别)
一个、多个
或没有
数据的
平均水平
数据的
中间水平
数据的
集中水平
知识梳理
在统计中,用( )作为一组数据的代表比较稳定可靠,它与这组数据中的每一个数都有关系,对这组数据所包含的信息的反映也是充分,但容易受极端数据的影响。用( )或( )作为一组数据的代表,可靠性比较差,但它们通常不受极端数据的影响,并且算法简便。当一组数据中个别数据变动较大时,适合选择( )或( )来表示这组数据的集中趋势。
平均数
中位数
众数
中位数
众数
知识梳理
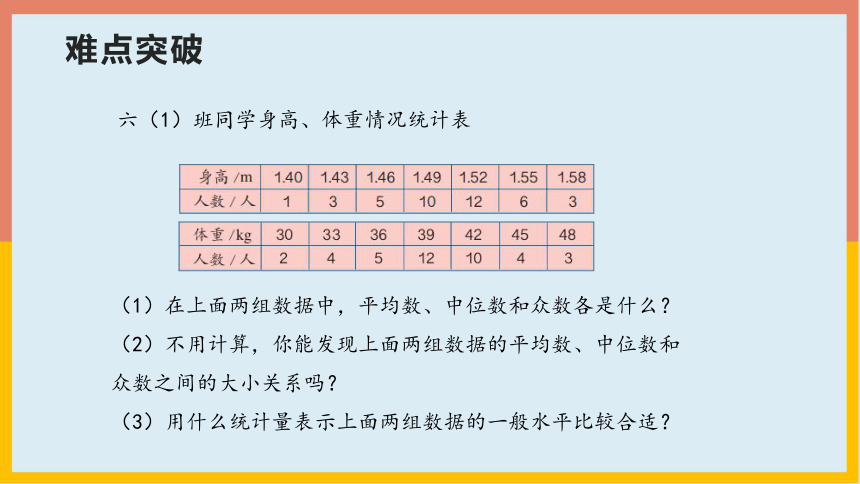
六(1)班同学身高、体重情况统计表
(1)在上面两组数据中,平均数、中位数和众数各是什么?
(2)不用计算,你能发现上面两组数据的平均数、中位数和众数之间的大小关系吗?
(3)用什么统计量表示上面两组数据的一般水平比较合适?
难点突破
(1)
身高:
平均数:(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
≈1.50(m)
体重:
平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的身高。所以中位数是1.52。
众数:1.52。
中位数:就是第20、21名之间的体重。所以中位数是39。
众数:39。
难点突破
(2)答:平均数有时比众数大。有时比众数小。
(3)答:用平均数表示比较合适。因为它与这组数据中的每个数据都有关系。
难点突破
(1)(9.8+9.7×2+9.6×4+9.5+9.4×2+9.1)÷11=9.5455(分)
(2) 因为平均数它与一组数据中的每个数据都有关系,它易受极端数据的影响,所以为了减少这种影响,在评分时就采取去掉一个最高分和一个最低分,再计算平均数,这样做是合理的。
在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
(1)这组数据的平均数是多少?
(2)如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,平均分是多少?你认为这样做是否有道理?为什么?
巩固练习
学校举办英语百词听写竞赛,五(1)班和五(2)班参赛选手的成绩如下:
五(1)班:88 87 88 87 85 96 98 90 87 91 93
99 87 95 88 92 94 88 87 88
五(2)班:82 96 87 89 94 95 83 99 92 84 93
97 85 98 99 88 91 90 81 80
这组数据的众数各是多少?你发现了什么?
五(1)班:87和88,五(2)班没有。
在一组数据中,众数可能不止一个,也可能没有众数。
巩固练均数、中位数和众数
平均数:数据的总和除以个数
中位数:先从小到大排列,再找最中间的一个或中间两
个数字的平均数。
众 数:出现次数最多的。
本课小结
阳光公司员工的工资情况表
如果你是阿Q,你是如何看待阳光公司的员工工资?
作业布置
员工 经 理 副 经理 职员A 职员B 职员C 职员D 职员E
月薪(元) 5000 3500 1200 1200 1000 1000 1000
再见
整理与复均数、中位数和众数
1.掌握平均数、中位数、众数的初步知识;
2.进一步理解平均数、中位数、众数这三种统计量的实际意义;
3.养成用数学观点解决实际问题的习惯。
学习目标
平均数、中位数、众数的概念
1.若干个数相加的和,除以这些数的个数所得的结果是这些数的平均数。
2.一组数据,把它们从小到大进行排列。如果有奇数个,那么中间的数就是这种数据的中位数;如果有偶数个,那么中间的两个数的平均数是这组数据的中位数。
3.在一组数中,出现频率最高的数是众数。
知识梳理
平均数: 反映总体平均水平。
中位数:反映中等水平。
众 数:反映多数集中水平。
知识梳理
平均数、中位数和众数的数量和意义
平均数 中位数 众数
数量
意义
一个
一个(奇、偶有别)
一个、多个
或没有
数据的
平均水平
数据的
中间水平
数据的
集中水平
知识梳理
在统计中,用( )作为一组数据的代表比较稳定可靠,它与这组数据中的每一个数都有关系,对这组数据所包含的信息的反映也是充分,但容易受极端数据的影响。用( )或( )作为一组数据的代表,可靠性比较差,但它们通常不受极端数据的影响,并且算法简便。当一组数据中个别数据变动较大时,适合选择( )或( )来表示这组数据的集中趋势。
平均数
中位数
众数
中位数
众数
知识梳理
六(1)班同学身高、体重情况统计表
(1)在上面两组数据中,平均数、中位数和众数各是什么?
(2)不用计算,你能发现上面两组数据的平均数、中位数和众数之间的大小关系吗?
(3)用什么统计量表示上面两组数据的一般水平比较合适?
难点突破
(1)
身高:
平均数:(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
≈1.50(m)
体重:
平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的身高。所以中位数是1.52。
众数:1.52。
中位数:就是第20、21名之间的体重。所以中位数是39。
众数:39。
难点突破
(2)答:平均数有时比众数大。有时比众数小。
(3)答:用平均数表示比较合适。因为它与这组数据中的每个数据都有关系。
难点突破
(1)(9.8+9.7×2+9.6×4+9.5+9.4×2+9.1)÷11=9.5455(分)
(2) 因为平均数它与一组数据中的每个数据都有关系,它易受极端数据的影响,所以为了减少这种影响,在评分时就采取去掉一个最高分和一个最低分,再计算平均数,这样做是合理的。
在某市举行的青年歌手大奖赛中,11位评委给一位歌手的打分如下。
(1)这组数据的平均数是多少?
(2)如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,平均分是多少?你认为这样做是否有道理?为什么?
巩固练习
学校举办英语百词听写竞赛,五(1)班和五(2)班参赛选手的成绩如下:
五(1)班:88 87 88 87 85 96 98 90 87 91 93
99 87 95 88 92 94 88 87 88
五(2)班:82 96 87 89 94 95 83 99 92 84 93
97 85 98 99 88 91 90 81 80
这组数据的众数各是多少?你发现了什么?
五(1)班:87和88,五(2)班没有。
在一组数据中,众数可能不止一个,也可能没有众数。
巩固练均数、中位数和众数
平均数:数据的总和除以个数
中位数:先从小到大排列,再找最中间的一个或中间两
个数字的平均数。
众 数:出现次数最多的。
本课小结
阳光公司员工的工资情况表
如果你是阿Q,你是如何看待阳光公司的员工工资?
作业布置
员工 经 理 副 经理 职员A 职员B 职员C 职员D 职员E
月薪(元) 5000 3500 1200 1200 1000 1000 1000
再见
