4.2.2反比例关系(课件) 数学六年级下册(共23张PPT)人教版
文档属性
| 名称 | 4.2.2反比例关系(课件) 数学六年级下册(共23张PPT)人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 495.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
反比例关系
初步理解反比例的意义。
学会根据反比例的意义判断两种相关联的量是不是成反比例。
1、六年级各班订阅《趣味数学》杂志的情况如下表:
订阅《趣味数学》的总价和数量成正比例吗?为什么?
成正比例,因为它们的比值相等。
2、做同一种服装,做的套数和用布的米数如下表:
做的套数和用布的米数成正比例吗?为什么?
做的套数和用布的米数成正比例,因为它们的比值相等。
复习旧知
两种量,杯子的底面积和水的高度。
表中有几种量?
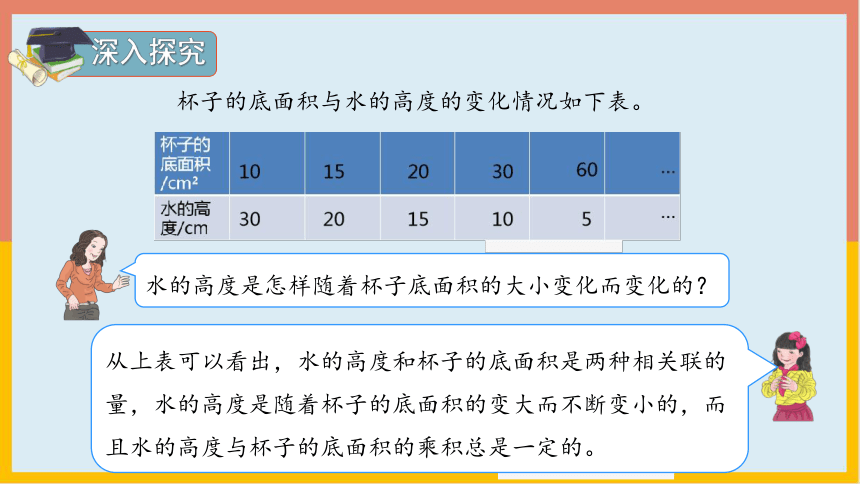
杯子的底面积与水的高度的变化情况如下表。
深入探究
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。
水的高度是怎样随着杯子底面积的大小变化而变化的?
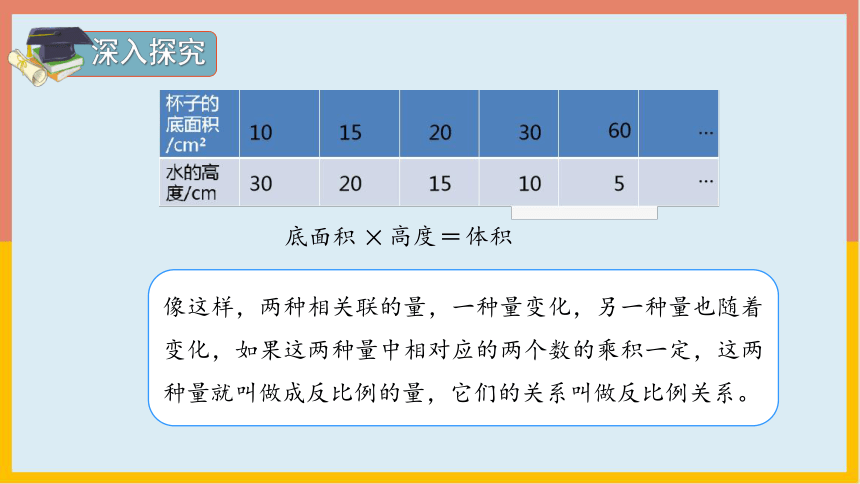
杯子的底面积与水的高度的变化情况如下表。
深入探究
积300,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
相对应的杯子的底面积与水的高度的乘积分别是多少?
30×10=20×15=15×20=…=300 。
底面积
=
体积
×
高度
深入探究
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
底面积
=
体积
×
高度
深入探究
在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
底面积
高度
=
体积
×
深入探究
如果用速度和时间表示两种相关联的量,用k表示它们的乘积(一定),反比例关系可以用下面的式子表示:
时间 ×速度=k
深入探究
你能举出生活中反比例关系的例子吗?
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
深入探究
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和运货的次数两种量,它们是相关联的量。
1、啤酒厂要运走一批啤酒,运输情况如下表:
每次运走的吨数 1 2 3 5 6 …
运的次数 30 15 10 6 5 …
巩固练习
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么。
30×1=15×2=10×3=6 ×5=5×6=30,这个积表示运货的总吨数。
1、啤酒厂要运走一批啤酒,运输情况如下表:
每次运走的吨数 1 2 3 5 6 …
运的次数 30 15 10 6 5 …
巩固练习
(3)运货的次数与每天运的吨数成反比例关系吗?为什么?
运货的次数与每天运的吨数成反比例关系,因为运货的天数与每天运的吨数的乘积一定。
1、啤酒厂要运走一批啤酒,运输情况如下表:
每次运走的吨数 1 2 3 5 6 …
运的次数 30 15 10 6 5 …
巩固练习
(1)燃气的数量一定,使用天数与每天的平均用燃气量。
每天的平均用燃气量与使用天数是两种相关量,因为每天的平均用燃气量×使用天数=燃气的总量(一定),所以使用天数与每天的平均用燃气量成反比例。
2、判断下面各题中的两种量是否成反比例关系,并说明理由。
巩固练习
(2)方队的人数一定,方队的列数与每列的人数。
每列的人数和列数是两种相关联的量,因为每列的人数×列数=方队的人数(一定),所以每列的人数和列数成反比例。
2、判断下面各题中的两种量是否成反比例关系,并说明理由。
巩固练习
(3)学校计划植500棵树,已植的棵树与未植的棵树。
已植的棵树与未植的棵树是两种相关联的量,因为已植的棵树+未植的棵树=学校计划植500棵树(一定),也就是和一定,所以已植的棵树与未植的棵树不成比例。
2、判断下面各题中的两种量是否成反比例关系,并说明理由。
巩固练习
2
5
1
3
0.5
10
a
b
8
20
30
1
3、下表中a和b两个量成反比例关系,请把表格填写完整。
1.25
巩固练习
路程 、速度、时间三个相关联的量,并有路程 =速度×时间。
(1)当时间一定时,路程 与速度成( )比例关系。
(2)当路程 一定时,时间与速度成( )比例关系。
(3)当速度一定时,时间与路程 成( )比例关系。
反
正
正
4、想一想,填一填。
巩固练习
5. 有一篇文章,编辑设计了以下几种排版方案。
每页字数与页数成反比例关系。因为它们的乘积一定。
每页字数与页数成反比例吗?为什么?
每页字数 200 300 400 500 600
页 数 60 40 30 24 20
巩固练习
01
02
如果用速度和时间表示两种相关联的量,用k表示它们的乘积(一定),反比例关系可以用下面的式子表示:时间 ×速度=k
反比例关系
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。
本节总结
1、在线完成反比例关系课后作业。
2、你能说说什么样的两种量成反比例关系。
布置作业
再见
反比例关系
初步理解反比例的意义。
学会根据反比例的意义判断两种相关联的量是不是成反比例。
1、六年级各班订阅《趣味数学》杂志的情况如下表:
订阅《趣味数学》的总价和数量成正比例吗?为什么?
成正比例,因为它们的比值相等。
2、做同一种服装,做的套数和用布的米数如下表:
做的套数和用布的米数成正比例吗?为什么?
做的套数和用布的米数成正比例,因为它们的比值相等。
复习旧知
两种量,杯子的底面积和水的高度。
表中有几种量?
杯子的底面积与水的高度的变化情况如下表。
深入探究
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。
水的高度是怎样随着杯子底面积的大小变化而变化的?
杯子的底面积与水的高度的变化情况如下表。
深入探究
积300,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
相对应的杯子的底面积与水的高度的乘积分别是多少?
30×10=20×15=15×20=…=300 。
底面积
=
体积
×
高度
深入探究
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
底面积
=
体积
×
高度
深入探究
在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
底面积
高度
=
体积
×
深入探究
如果用速度和时间表示两种相关联的量,用k表示它们的乘积(一定),反比例关系可以用下面的式子表示:
时间 ×速度=k
深入探究
你能举出生活中反比例关系的例子吗?
如果长方形的面积一定,长与宽成反比例关系。
如果总价一定,单价与数量成反比例关系。
深入探究
(1)表中有哪两种量?它们是不是相关联的量?
表中有每天运的吨数和运货的次数两种量,它们是相关联的量。
1、啤酒厂要运走一批啤酒,运输情况如下表:
每次运走的吨数 1 2 3 5 6 …
运的次数 30 15 10 6 5 …
巩固练习
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么。
30×1=15×2=10×3=6 ×5=5×6=30,这个积表示运货的总吨数。
1、啤酒厂要运走一批啤酒,运输情况如下表:
每次运走的吨数 1 2 3 5 6 …
运的次数 30 15 10 6 5 …
巩固练习
(3)运货的次数与每天运的吨数成反比例关系吗?为什么?
运货的次数与每天运的吨数成反比例关系,因为运货的天数与每天运的吨数的乘积一定。
1、啤酒厂要运走一批啤酒,运输情况如下表:
每次运走的吨数 1 2 3 5 6 …
运的次数 30 15 10 6 5 …
巩固练习
(1)燃气的数量一定,使用天数与每天的平均用燃气量。
每天的平均用燃气量与使用天数是两种相关量,因为每天的平均用燃气量×使用天数=燃气的总量(一定),所以使用天数与每天的平均用燃气量成反比例。
2、判断下面各题中的两种量是否成反比例关系,并说明理由。
巩固练习
(2)方队的人数一定,方队的列数与每列的人数。
每列的人数和列数是两种相关联的量,因为每列的人数×列数=方队的人数(一定),所以每列的人数和列数成反比例。
2、判断下面各题中的两种量是否成反比例关系,并说明理由。
巩固练习
(3)学校计划植500棵树,已植的棵树与未植的棵树。
已植的棵树与未植的棵树是两种相关联的量,因为已植的棵树+未植的棵树=学校计划植500棵树(一定),也就是和一定,所以已植的棵树与未植的棵树不成比例。
2、判断下面各题中的两种量是否成反比例关系,并说明理由。
巩固练习
2
5
1
3
0.5
10
a
b
8
20
30
1
3、下表中a和b两个量成反比例关系,请把表格填写完整。
1.25
巩固练习
路程 、速度、时间三个相关联的量,并有路程 =速度×时间。
(1)当时间一定时,路程 与速度成( )比例关系。
(2)当路程 一定时,时间与速度成( )比例关系。
(3)当速度一定时,时间与路程 成( )比例关系。
反
正
正
4、想一想,填一填。
巩固练习
5. 有一篇文章,编辑设计了以下几种排版方案。
每页字数与页数成反比例关系。因为它们的乘积一定。
每页字数与页数成反比例吗?为什么?
每页字数 200 300 400 500 600
页 数 60 40 30 24 20
巩固练习
01
02
如果用速度和时间表示两种相关联的量,用k表示它们的乘积(一定),反比例关系可以用下面的式子表示:时间 ×速度=k
反比例关系
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。
本节总结
1、在线完成反比例关系课后作业。
2、你能说说什么样的两种量成反比例关系。
布置作业
再见
