6.4.1探究模式的策略(课件) 数学六年级下册(共22张PPT)人教版
文档属性
| 名称 | 6.4.1探究模式的策略(课件) 数学六年级下册(共22张PPT)人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 409.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 06:23:56 | ||
图片预览






文档简介
(共22张PPT)
探究模式的策略
理解点与点之间连线段的内在规律,掌握正确计算线段数的方法。
通过观察、分析、归纳等过程,进一步发展合情推理能力和问题解决能力。
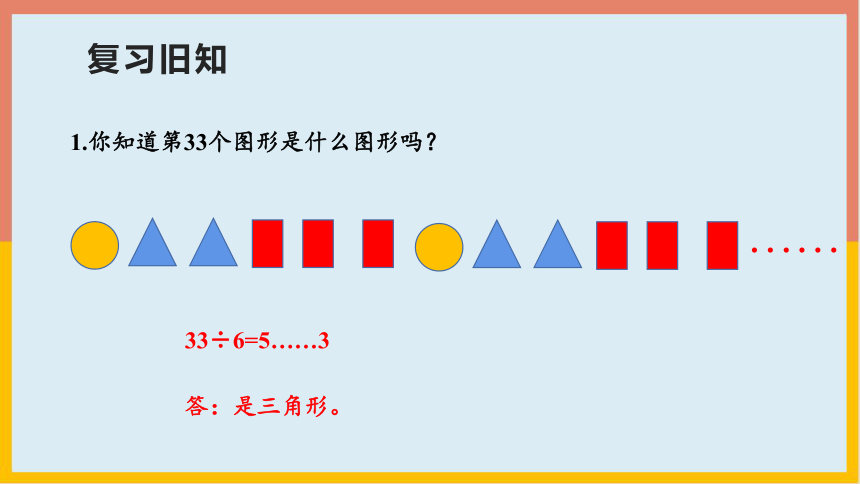
33÷6=5……3
答:是三角形。
……
1.你知道第33个图形是什么图形吗?
复习旧知
2. 4位同学排一行表演小合唱,丁刚同学担任领唱,固定在左起第二个位置上,其余同学任意排。有( )种不同的排法。
6
复习旧知
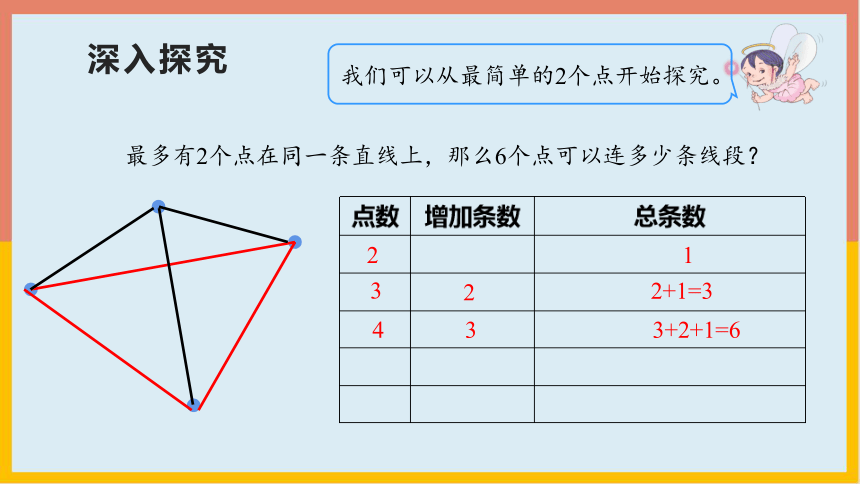
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
导入新课
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
深入探究
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
4
3
3+2+1=6
深入探究
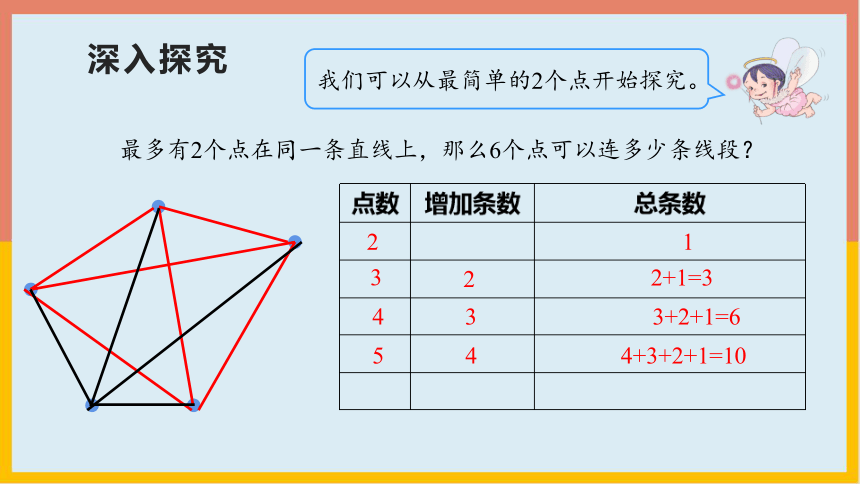
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
4
3
3+2+1=6
5
4
4+3+2+1=10
深入探究
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
4
3
3+2+1=6
5
4
4+3+2+1=10
6
5
5+4+3+2+1=15
深入探究
观察“点数”和“增加条数”,你发现了什么规律?
增加的条数总是比点数少1。
深入探究
说说你发现的规律吧!
要计算一共有几条,实际上就是从1+2+3+…一直加到比点数少l的数。
深入探究
按照规律,8个点能连几条线段?
1+2+3+4+5+6+7
=(1+7)+(2+6)+(3+5)+4
=8×3+4
=28(条)
为什么有8个点,列式却依次加到7呢?
深入探究
化繁为简
在本节课的探究中,我们运用哪些探究方法?
画图、数形结合、枚举
有序思考
探究规律
深入探究
1. 根据上面的规律,你知道11个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11×5
=55(条)
2、根据规律,你知道18个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17
=(1+17)+(2+16)+(3+15)+……+(8+10)+9
=18×8+9
=153(条)
3、观察下图,想一想。你有什么发现?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
6×6=36(个)
12×12=144(个)
3、观察下图,想一想。
(1)第6幅图有多少个棋子?第12幅图呢?
3、观察下图,想一想。每边的棋子数与图形的序号有什么关系?
(2)第n幅图每边有多少个棋子?第n幅图有多少个棋子?
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
4. 中国、日本、英国、美国、加拿大每两个球队进行一场比赛,一共踢几场球?
1+2+3+4=10(场)
答:一共踢10场球。
5、 每两个人握1次手,4个同学一共要握几次手?(学生相互握手)全班30名同学同学又该握几次呢?
1+2+3=6(次)
答:4个同学一共要握6次手。
1+2+3+……+29=435(次)
答:30个同学一共要握435次手。
6. 找规律填数
2,10,19,29, ,52 , …
1,5,11,19,29, , 55,…
40
65
41
探究问题时,我们可以运用画图、数形结合、枚举的方法。
探究模式的策略
探究问题时,我们可以运用化繁为简的策略。
探究问题时,我们可以运用有序思考、探究规律的策略。
探究模式的策略
理解点与点之间连线段的内在规律,掌握正确计算线段数的方法。
通过观察、分析、归纳等过程,进一步发展合情推理能力和问题解决能力。
33÷6=5……3
答:是三角形。
……
1.你知道第33个图形是什么图形吗?
复习旧知
2. 4位同学排一行表演小合唱,丁刚同学担任领唱,固定在左起第二个位置上,其余同学任意排。有( )种不同的排法。
6
复习旧知
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
导入新课
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
深入探究
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
4
3
3+2+1=6
深入探究
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
4
3
3+2+1=6
5
4
4+3+2+1=10
深入探究
我们可以从最简单的2个点开始探究。
2
最多有2个点在同一条直线上,那么6个点可以连多少条线段?
1
3
2
2+1=3
4
3
3+2+1=6
5
4
4+3+2+1=10
6
5
5+4+3+2+1=15
深入探究
观察“点数”和“增加条数”,你发现了什么规律?
增加的条数总是比点数少1。
深入探究
说说你发现的规律吧!
要计算一共有几条,实际上就是从1+2+3+…一直加到比点数少l的数。
深入探究
按照规律,8个点能连几条线段?
1+2+3+4+5+6+7
=(1+7)+(2+6)+(3+5)+4
=8×3+4
=28(条)
为什么有8个点,列式却依次加到7呢?
深入探究
化繁为简
在本节课的探究中,我们运用哪些探究方法?
画图、数形结合、枚举
有序思考
探究规律
深入探究
1. 根据上面的规律,你知道11个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11×5
=55(条)
2、根据规律,你知道18个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17
=(1+17)+(2+16)+(3+15)+……+(8+10)+9
=18×8+9
=153(条)
3、观察下图,想一想。你有什么发现?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
6×6=36(个)
12×12=144(个)
3、观察下图,想一想。
(1)第6幅图有多少个棋子?第12幅图呢?
3、观察下图,想一想。每边的棋子数与图形的序号有什么关系?
(2)第n幅图每边有多少个棋子?第n幅图有多少个棋子?
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
4. 中国、日本、英国、美国、加拿大每两个球队进行一场比赛,一共踢几场球?
1+2+3+4=10(场)
答:一共踢10场球。
5、 每两个人握1次手,4个同学一共要握几次手?(学生相互握手)全班30名同学同学又该握几次呢?
1+2+3=6(次)
答:4个同学一共要握6次手。
1+2+3+……+29=435(次)
答:30个同学一共要握435次手。
6. 找规律填数
2,10,19,29, ,52 , …
1,5,11,19,29, , 55,…
40
65
41
探究问题时,我们可以运用画图、数形结合、枚举的方法。
探究模式的策略
探究问题时,我们可以运用化繁为简的策略。
探究问题时,我们可以运用有序思考、探究规律的策略。
