6.1.4比和比例(课件) 数学六年级下册(共28张PPT)人教版
文档属性
| 名称 | 6.1.4比和比例(课件) 数学六年级下册(共28张PPT)人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 882.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
比和比例
在整理和复习中,经历对比和比例有关知识系统复习与整理的过程。
进一步理解并掌握比和比例有关知识,能用比和比例有关知识解决实际问题。
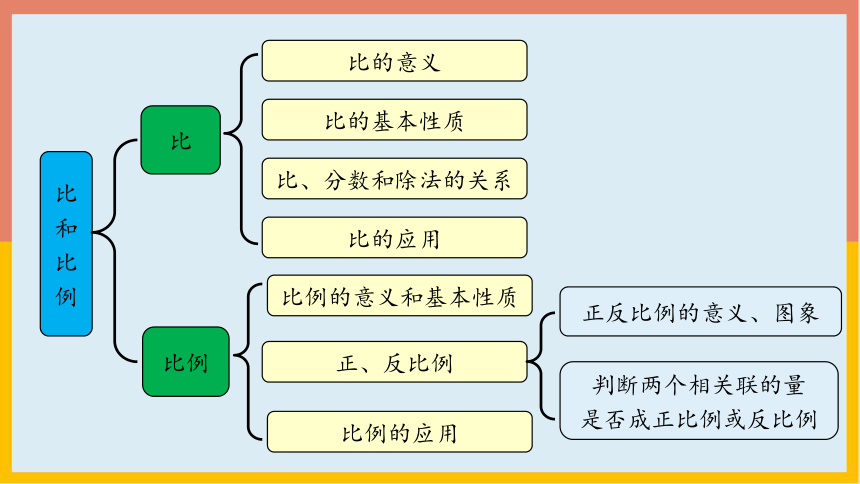
比和比例
比
比的基本性质
比的意义
比、分数和除法的关系
比例
比的应用
正、反比例
比例的意义和基本性质
比例的应用
判断两个相关联的量
是否成正比例或反比例
正反比例的意义、图象
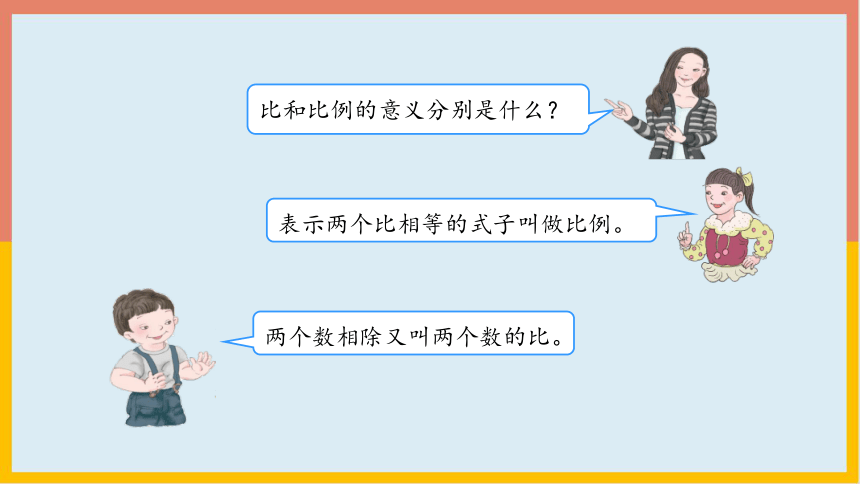
比和比例的意义分别是什么?
表示两个比相等的式子叫做比例。
两个数相除又叫两个数的比。
比和比例的基本性质分别是什么?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比例的两个外项的积等于两个内项的积。
正、反比例的意义分别是什么?
正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定。
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
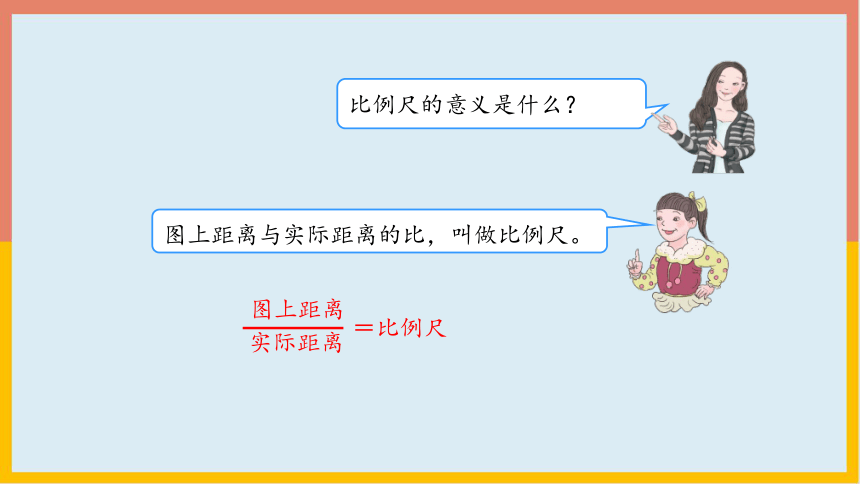
比例尺的意义是什么?
图上距离与实际距离的比,叫做比例尺。
实际距离
图上距离
=比例尺
1、两个数相除又叫做两个数的( )。
2、比的前项相当于分数的( )、除法中的( ),比的后项相当于分数的( )、除法中的( )。
3、比的前项和后项同时乘(或除)相同的数(0除外)比值不变,这叫做( )。
比
分子
被除数
分母
除数
比的基本性质
4、表示两个比相等的式子叫作( )。
5、判断了两个比是否成比例,看看这两个比的比值是否( )。
6、在比例里,两个内项的积等于两个外项的积,这叫做( )。
比例
相等
比例的基本性质
7、两种相关联的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。用字母表示是( )。
8、表示正比例关系的图象是从横轴和竖轴的交点画出的一条( ),两种量的所有对应点都在( )上。
变化
比值
正比例
射线
这条射线
9、两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( )。它们的关系叫做( )。
10、如果用x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面的式子表示:( )。
反比例
反比例关系
xy=k(一定)
两个数相除又叫两个数的比 ,写比时一般要写成最简比。
1、填一填。
(1)六年级二班有男生21人,女生23人。男、女生人数的比是( ),女生与全班人数的比是( )。
(2)一辆汽车3小时行驶210千米。这辆汽车行驶的路程与时间的比是( ),行驶的时间与路程的比是( )。
7:8
8:15
70:1
1:70
解比例是根据比例的基本性质,比例的两个外项的积等于两个内项的积。
2、解比例:
9:x=3:4
解:3x= 9×4
3x=36
x=12
解:0.1x=100×0.01
0.1x=1
x=10
3、正比例的图像:
下面的图像表示一幅地图的图上距离和实际距离的关系。
(1)根据上面的图像,你能说出这幅地图的比例尺吗?图上距离和实际距离成什么比例?为什么?
这幅地图的比例尺是1:4000 ; 图上距离和实际距离成正比例,它们的比值相等。
表示正比例关系的图象是从横轴和竖轴的交点画出的一条射线,相对应的两种量的所有对应点都在这条直线上。
3、正比例的图像:
下面的图像表示一幅地图的图上距离和实际距离的关系。
(2)在这幅地图上,量得两地的图上距离是12厘米,两地的实际距离是多少米?
两地的实际距离是480米。
A
两个数相除又叫做两个数的比。比的前项和后项同时乘(或除)相同的数(0除外)比值不变,这叫做基本性质。
B
表示两个比相等的式子叫作比例。在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
比和比例
C
正比例:
反比例:
x×y=k(一定)
1、甲车4小时行驶360km,乙车3小时行驶240km。
(1)甲车行驶的路程与时间的比是( )。
(2)乙车行驶的路程与时间的比是( )。
(3)乙车与甲车行驶的路程比是( )。
(4)甲车与乙车行驶的时间比是( )。
90:1
80:1
2:3
4:3
2、填一填。
(1)如果a×5=b×12,那么a:b=( ):( )。
(2)配制一种盐水,盐和水质量的比是1:24,盐和盐水质量的比是( ),水和盐水质量的比是( )。
(3)公鸡与母鸡只数的比是3:7,公鸡占总只数的 ,母鸡
占总只数的 。
12 5
1:25
24:25
3
10
7
10
3、解比例。
9:5=4.5:x
解:9x= 4.5×5
9x=22.5
x=2.5
解:0.4x=2.8×0.1
0.4x=0.28
x=0.7
4、判断每张表中的两种量是成正比例、反比例,还是不成比例,并说明理由。
成正比例, 因为比的前项和后项的比值一定。
成正比例, 因为小麦的质量和磨面粉质量的比值一定。
成反比例, 因为三角形的底和高的乘积一定。
不成比例,园的半径和面积的比值不一定。
5、下图表示一辆汽车在高速公路上行驶的路程和耗油量的关系。
(1)这辆汽车在高速公路上行驶的路程和耗油量成正比例吗?为什么?
成正比例,因为行驶的路程和耗油量比值相等。
5、下图表示一辆汽车在高速公路上行驶的路程和耗油量的关系。
(2)根据图形判断,行驶75千米耗油多少升?
6升
5、下图表示一辆汽车在高速公路上行驶的路程和耗油量的关系。
(3)汽车在市区行驶,每行50千米耗油6升,照这样的耗油量,在上图中描出行驶50千米、100千米……路程和耗油量对应的点,再按顺序连接起来。
解:设甲、乙两地之间的实际距离为x厘米。
1:25000 = 15:x
x = 15×25000
x = 375000
6、在比例尺是1:25000的地图上量得甲、乙两地之间的距离是15厘米,如果把它改画在比例尺为1:20000的地图上,甲、乙两地的图上距离应画多长?
设甲、乙两地之间的图上距离为y厘米。
1:20000 = y:375000
20000y = 375000
y = 18.75
6、在比例尺是1:25000的地图上量得甲、乙两地之间的距离是20厘米,如果把它改画在比例尺为1:20000的地图上,甲、乙两地的图上距离应画多长?
答:甲、乙两地的图上距离应画18.75厘米。
7、(1)大小两个圆的半径之比是2:5。它们的直径之比是( ),面积之比是( )。
(2)在一个比例中,两个内项互为倒数,一个外项是0.5,另一个 外项是( )。
(3)在比例里,两个外项的积一定,两个内项成( )比例。
4:25
2
反
2:5
在线完成6.1.4比和比例课后作业。
再见
比和比例
在整理和复习中,经历对比和比例有关知识系统复习与整理的过程。
进一步理解并掌握比和比例有关知识,能用比和比例有关知识解决实际问题。
比和比例
比
比的基本性质
比的意义
比、分数和除法的关系
比例
比的应用
正、反比例
比例的意义和基本性质
比例的应用
判断两个相关联的量
是否成正比例或反比例
正反比例的意义、图象
比和比例的意义分别是什么?
表示两个比相等的式子叫做比例。
两个数相除又叫两个数的比。
比和比例的基本性质分别是什么?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比例的两个外项的积等于两个内项的积。
正、反比例的意义分别是什么?
正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定。
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
比例尺的意义是什么?
图上距离与实际距离的比,叫做比例尺。
实际距离
图上距离
=比例尺
1、两个数相除又叫做两个数的( )。
2、比的前项相当于分数的( )、除法中的( ),比的后项相当于分数的( )、除法中的( )。
3、比的前项和后项同时乘(或除)相同的数(0除外)比值不变,这叫做( )。
比
分子
被除数
分母
除数
比的基本性质
4、表示两个比相等的式子叫作( )。
5、判断了两个比是否成比例,看看这两个比的比值是否( )。
6、在比例里,两个内项的积等于两个外项的积,这叫做( )。
比例
相等
比例的基本性质
7、两种相关联的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。用字母表示是( )。
8、表示正比例关系的图象是从横轴和竖轴的交点画出的一条( ),两种量的所有对应点都在( )上。
变化
比值
正比例
射线
这条射线
9、两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( )。它们的关系叫做( )。
10、如果用x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面的式子表示:( )。
反比例
反比例关系
xy=k(一定)
两个数相除又叫两个数的比 ,写比时一般要写成最简比。
1、填一填。
(1)六年级二班有男生21人,女生23人。男、女生人数的比是( ),女生与全班人数的比是( )。
(2)一辆汽车3小时行驶210千米。这辆汽车行驶的路程与时间的比是( ),行驶的时间与路程的比是( )。
7:8
8:15
70:1
1:70
解比例是根据比例的基本性质,比例的两个外项的积等于两个内项的积。
2、解比例:
9:x=3:4
解:3x= 9×4
3x=36
x=12
解:0.1x=100×0.01
0.1x=1
x=10
3、正比例的图像:
下面的图像表示一幅地图的图上距离和实际距离的关系。
(1)根据上面的图像,你能说出这幅地图的比例尺吗?图上距离和实际距离成什么比例?为什么?
这幅地图的比例尺是1:4000 ; 图上距离和实际距离成正比例,它们的比值相等。
表示正比例关系的图象是从横轴和竖轴的交点画出的一条射线,相对应的两种量的所有对应点都在这条直线上。
3、正比例的图像:
下面的图像表示一幅地图的图上距离和实际距离的关系。
(2)在这幅地图上,量得两地的图上距离是12厘米,两地的实际距离是多少米?
两地的实际距离是480米。
A
两个数相除又叫做两个数的比。比的前项和后项同时乘(或除)相同的数(0除外)比值不变,这叫做基本性质。
B
表示两个比相等的式子叫作比例。在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
比和比例
C
正比例:
反比例:
x×y=k(一定)
1、甲车4小时行驶360km,乙车3小时行驶240km。
(1)甲车行驶的路程与时间的比是( )。
(2)乙车行驶的路程与时间的比是( )。
(3)乙车与甲车行驶的路程比是( )。
(4)甲车与乙车行驶的时间比是( )。
90:1
80:1
2:3
4:3
2、填一填。
(1)如果a×5=b×12,那么a:b=( ):( )。
(2)配制一种盐水,盐和水质量的比是1:24,盐和盐水质量的比是( ),水和盐水质量的比是( )。
(3)公鸡与母鸡只数的比是3:7,公鸡占总只数的 ,母鸡
占总只数的 。
12 5
1:25
24:25
3
10
7
10
3、解比例。
9:5=4.5:x
解:9x= 4.5×5
9x=22.5
x=2.5
解:0.4x=2.8×0.1
0.4x=0.28
x=0.7
4、判断每张表中的两种量是成正比例、反比例,还是不成比例,并说明理由。
成正比例, 因为比的前项和后项的比值一定。
成正比例, 因为小麦的质量和磨面粉质量的比值一定。
成反比例, 因为三角形的底和高的乘积一定。
不成比例,园的半径和面积的比值不一定。
5、下图表示一辆汽车在高速公路上行驶的路程和耗油量的关系。
(1)这辆汽车在高速公路上行驶的路程和耗油量成正比例吗?为什么?
成正比例,因为行驶的路程和耗油量比值相等。
5、下图表示一辆汽车在高速公路上行驶的路程和耗油量的关系。
(2)根据图形判断,行驶75千米耗油多少升?
6升
5、下图表示一辆汽车在高速公路上行驶的路程和耗油量的关系。
(3)汽车在市区行驶,每行50千米耗油6升,照这样的耗油量,在上图中描出行驶50千米、100千米……路程和耗油量对应的点,再按顺序连接起来。
解:设甲、乙两地之间的实际距离为x厘米。
1:25000 = 15:x
x = 15×25000
x = 375000
6、在比例尺是1:25000的地图上量得甲、乙两地之间的距离是15厘米,如果把它改画在比例尺为1:20000的地图上,甲、乙两地的图上距离应画多长?
设甲、乙两地之间的图上距离为y厘米。
1:20000 = y:375000
20000y = 375000
y = 18.75
6、在比例尺是1:25000的地图上量得甲、乙两地之间的距离是20厘米,如果把它改画在比例尺为1:20000的地图上,甲、乙两地的图上距离应画多长?
答:甲、乙两地的图上距离应画18.75厘米。
7、(1)大小两个圆的半径之比是2:5。它们的直径之比是( ),面积之比是( )。
(2)在一个比例中,两个内项互为倒数,一个外项是0.5,另一个 外项是( )。
(3)在比例里,两个外项的积一定,两个内项成( )比例。
4:25
2
反
2:5
在线完成6.1.4比和比例课后作业。
再见
