2021-2022学年高中人教版(2019)必修第二册 8.1 功与功率 教学课件(36张PPT)
文档属性
| 名称 | 2021-2022学年高中人教版(2019)必修第二册 8.1 功与功率 教学课件(36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
功与功率
任何人类活动都离不开能量
现代化的生活离不开电厂供应的电能
现代交通离不开燃料燃烧释放的化学能
核电站要利用原子核裂变时释放的核能
植物的生长依赖太阳能
不同形式的能量可以互相转化,并且能量的转化与功的概念紧密相连
问题导入
G
F拉
v
力对物体做的功:为力的大小与重物移动距离的乘积。
F拉
v
物体运动的方向与力的方向不一致,这时应当怎样计算 功呢?
W=FL
温故知新
功的定义:如果一个物体受到力的作用,并且在这个力的方向上通过一段位移 ,我们就说这个力对物体做了功。
F
l
F
(1)作用在物体上的力
(2)物体在力的方向上通过的位移
做功的两个条件:
温故知新
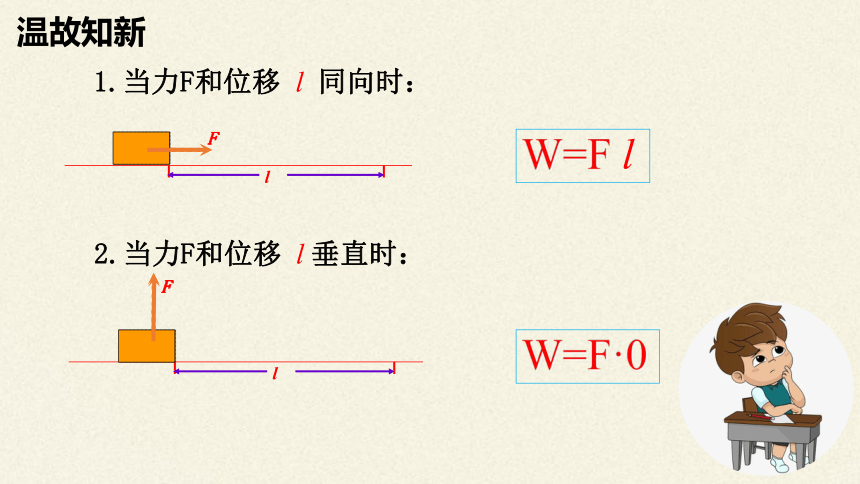
1.当力F和位移 l 同向时:
F
l
F
W=F l
2.当力F和位移 l 垂直时:
W=F·0
F
l
F
一、功
l
F
F
α
F
α
F
α
W2 = 0
F2
F1
当力F和位移 l 成α时:
WF1=F1·l
WF2=F2·0
另辟蹊径:
除了分解力以外还可以分解位移
F
l
l1
l2
α
l1=lcosα
l2=lsinα
W2= 0
W= F lcosα
在力方向发生的位移
W1= Fl 1= Flcos α
一、功
1.公式:W = F lcosα 力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。
2.国际单位:
焦耳(简称:焦 ——符号:J)
1J=1N×1m=1N·m
3.功是标量,没有方向,但有正负。
4.说明
(1) 功是过程量,对应一段时间或位移是力对空间的积累效果;故计算功时一定要指明是哪个力在哪个过程对物体做的功。
(2)公式W = Fl cosα只适用于计算恒力的功,l是物体的位移,不是路程。
F
m
M
l
W=Flcosα的理解
①F是恒力
②l是位移
F
l
③F和l必须同时存在
例如运动员用50N的力将蓝球水平扔出,蓝球在空飞了2m被截住,则运动员对蓝球做的功是100J。对吗?
G
F推
v
不做功
做功
G
v
不做功
F不做功
出手瞬间对球做功
④a是位移与力的夹角
α
起点相同时的夹角
【典例1 】如图表示物体在力F的作用下在水平面上发生了一段位移l,分别计算这三种情形下力F对物体做的功。设这三种情形下力F和位移l的大小都是一样的:F=10N,l=2m。角θ的大小如图所示。
F
l
l
l
二、正功和负功
W=Flcosα
①当α=π/2时,cosα=0,W=0。这表示力F的方向跟位移L的方向垂直,即力F不做功。
l
F1
②当0<α<π/2时, cosα>0,W>0,这表示力F1对物体做正功;
F2
③当π/2<α≤π时,cosα<0,W<0。这表示力F2对物体做负功。
④当α=0时,cosα=1,即W=Fl。
1. 正负不表示方向,也不表示大小。
负功的物理意义:
正功的物理意义:
表示该力是动力;
表示该力是阻力。
2.某力做多少负功,也可说成“物体克服该力做多少功”(取绝对值)。
v
f=5N
l=2m
A
B
F1
A
F2
B
如:-8J > 5J
正功和负功
思考:怎么比较功的大小?
比较绝对值
【典例2】一个质量m=150kg的雪橇,受到与水平方向成37°角的
斜向上方的拉力F=500N,在水平地面上移动的距离为5m,物体与
地面间的滑动摩擦力f=100N,cos 37°= 0.8。求
(1)各个力对物体所做的功
(2)各个力对物体做功的代数和
(3)物体所受的合力
(4)合力对物体做的功
三、总功的计算
三、总功的计算
1.分别求出每个力所做的功,然后求出所有功的代数和。即:
2.先求出物体所受的合力,然后再求出合力的功,即:
求总功的两种方法:
W总=F合Lcosα
【典例3】下列选项中,物体所受力F的大小相等,位移方向向右、大小相同。其中F做功最少的是( )
典例分析
【正确答案】D
典例分析
【典例4】如图所示,小明用与水平方向成角θ的轻绳拉木箱,绳中张力为F,沿水平地面向右移动了一段距离L,已知木箱与地面间的动摩擦因数为μ,木箱质量为m,木箱受到的( )
A.支持力做功为
B.重力做功为mgL
C.拉力做功为FL
D.滑动摩擦力做功为
【正确答案】D
情境引入
做同样的功
谁更快
【思考】起重机甲在60s内把1吨的货物匀速提高了5m,另一台起重机乙在30s内把1吨的货物匀速提高了5m。哪一台起重机做功快?如何比较它们做功的快慢?
提示:起重机乙做功快,做的功相同,用时少的做功快。
3.单位:在国际单位制中,功率的单位是瓦特,简称瓦,符号是W。
1W=1J/s,技术上常用千瓦(kW),1kW=1000W,1马力=735W
1.定义:力对物体做的功W,跟完成这些功所用时间t的比值叫功率.
4.物理意义:反映力对物体做功的快慢。
比值定义法
5.说明:功率是标量,计算功率时,一般不带正负号。
四、功率
2.定义式:
同时这个公式变形后给我们提供了一种求功的方法,即 W=pt.
即使是同一个力做功,做功的功率也可能是变化的,在一段时间内力对物体做功的功率,实际上是这段时间内力对物体做功的平均功率。
平均功率:描述在一段时间内做功的平均快慢
瞬时功率:表示在某一时刻做功的快慢
当 t 很短很短时,此式表示瞬时功率
当 t 表示一段时间时,此式表示平均功率
平均功率和瞬时功率
W=Flcosα
P=
t
W
P=Fvcosα
P=
t
Flcosα
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
v=
t
l
功率的另一种表达式
若v表示平均速度,则P表示平均功率
若v表示瞬时速度,则P表示瞬时功率
1.额定功率:是指机器正常工作时的最大输出功率,也就是机器铭
牌上的标称值。
2.实际功率:是指机器在工作中实际输出的功率。
额定功率和实际功率
(1)机器正常工作时实际功率总小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
(2)在日常生活中,某台机器的功率,或某物体做功的功率,实际上是指某个力对物体做功的功率。例如:汽车的功率就是汽车牵引力的功率,起重机吊起货物的功率就是钢绳拉力的功率。
1.功率是描述物体做功快慢程度的物理量
2.机械效率是描述机械做功时有效利用率的物理量
功率和机械效率区别
或
【典例4】如图所示为我国自行研制的新一代大型客机C919。假定其质量为m,起飞时在水平跑道上以加速度a做匀加速直线运动,受到的阻力大小为 ,当飞机速度为v时,则发动机输出的实际功率为( )
典例分析
【正确答案】B
A. B.
C. D.
【典例5】质量为m=10kg的物体放在粗糙的水平面上,物体与水平面间的动摩擦因数为 =0.25,现在大小为F=45N的水平拉力作用下从静止开始运动,通过一段s=4m的位移(g=10m/s2)求:
(1)该过程中拉力做的功;
(2)该过程拉力的平均功率和末状态的瞬时功率。
典例分析
【答案】(1)180J;(2)90W,180W;
【典例6】质量m=3kg的物体,在水平力F=6N的作用下,在光滑的水平面上从静止开始运动,运动时间t=3s,求:
(1)力F在t=3s内对物体做的功;
(2)力F在t=3s内对物体做功的平均功率;
(3)力F在3s末对物体做功的瞬时功率。
典例分析
【解析】a=F/m=2m/s2 ;l=v0t+1/2at2=9m,vt=v0+at=6m/s
(1)W=Fl=54J (2)P=W/t=18W (3)P1=FVt=36W
汽车启动
机车在行驶的过程中,发动机的最大功率等于额定功率。
P=F v
课堂引入
v
瞬时速度
功率
牵引力
机车的启动方式有两种:
1.以恒定功率P额启动;
2.在恒定的牵引力F作用下匀加速启动。
当F=F阻时,
a=0 ,v达到最大
保持 vm
匀速
v
F =
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
类型一:以恒定功率P额启动
F阻
F牵
F阻
F牵
vm
v—t 图象
加速阶段
的图象
匀速阶段
的图象
a减小的变加速运动
匀速运动
v0=0,P恒=P额
vm
v
t
0
1.F为变力时,发动机做的功只能用
W=Pt 计算,不能用W =Fl 计算。
总结:
2.达到最大速度的本质条件是:a=0
vm
v
t
0
说明:
3.达到最大速度时,有 P额=F阻vm
类型一:以恒定功率P额启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P =F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
类型二:以恒定加速度启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P =F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
类型二:以恒定加速度启动
机车做匀加速运动只能维持一段时间,当功率增大到额定功率时,匀加速运动结束,匀加速时间为:
t1=
P额
(ma+f阻)a
说明:
2.匀加速结束的条件是:P实=Pmax=P额
3.当匀加速结束时速度为v1,P额=Fv1=f阻Vm (其中F=ma+f阻)
t1
v1
v
t
0
vm
1.达到最大速度的本质条件:a=0
类型二:以恒定加速度启动
【典例1】(多选)按额定功率行驶的汽车,所受地面的阻力保持不变,则( )
A.汽车加速行驶时,牵引力不变,速度增大
B.汽车可以做匀加速运动
C.汽车加速行驶时,加速度逐渐减小,速度逐渐增大
D.汽车达到最大速度时,所受合力为零
典例分析
【正确答案】CD
【典例2】(多选)火车从车站开出做匀加速运动,若阻力与速度成正比,则( )
A.火车发动机的功率一定越来越大,牵引力越来越大
B.火车发动机的功率恒定不变,牵引力越来越小
C.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率这时应减小
D.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率一定跟此时速率的二次方成正比
【正确答案】ACD
典例分析
典例分析
【典例3】汽车的额定功率为60 kW,总质量为2×103 kg,运动中所受阻力恒为2 000 N.若汽车在额定功率下启动,求:
(1)当汽车的加速度是1 m/s2时的速度大小;
(2)汽车行驶的最大速度.
【答案】 (1)15 m/s (2)30 m/s
典例分析
【典例4】质量为m=4 t的机车,发动机的最大输出功率P=80 kW,运动阻力恒为Ff=2×103 N.
(1)若机车由静止开始以a=0.5 m/s2的加速度沿水平轨道做匀加速直线运动的过程中,求机车能达到的最大速度;
(2)若机车保持最大功率不变沿水平轨道行驶,求机车能达到的最大速度以及速度为10 m/s时机车的加速度.
【答案】 (1)20 m/s (2)40 m/s 1.5 m/s2
功与功率
任何人类活动都离不开能量
现代化的生活离不开电厂供应的电能
现代交通离不开燃料燃烧释放的化学能
核电站要利用原子核裂变时释放的核能
植物的生长依赖太阳能
不同形式的能量可以互相转化,并且能量的转化与功的概念紧密相连
问题导入
G
F拉
v
力对物体做的功:为力的大小与重物移动距离的乘积。
F拉
v
物体运动的方向与力的方向不一致,这时应当怎样计算 功呢?
W=FL
温故知新
功的定义:如果一个物体受到力的作用,并且在这个力的方向上通过一段位移 ,我们就说这个力对物体做了功。
F
l
F
(1)作用在物体上的力
(2)物体在力的方向上通过的位移
做功的两个条件:
温故知新
1.当力F和位移 l 同向时:
F
l
F
W=F l
2.当力F和位移 l 垂直时:
W=F·0
F
l
F
一、功
l
F
F
α
F
α
F
α
W2 = 0
F2
F1
当力F和位移 l 成α时:
WF1=F1·l
WF2=F2·0
另辟蹊径:
除了分解力以外还可以分解位移
F
l
l1
l2
α
l1=lcosα
l2=lsinα
W2= 0
W= F lcosα
在力方向发生的位移
W1= Fl 1= Flcos α
一、功
1.公式:W = F lcosα 力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。
2.国际单位:
焦耳(简称:焦 ——符号:J)
1J=1N×1m=1N·m
3.功是标量,没有方向,但有正负。
4.说明
(1) 功是过程量,对应一段时间或位移是力对空间的积累效果;故计算功时一定要指明是哪个力在哪个过程对物体做的功。
(2)公式W = Fl cosα只适用于计算恒力的功,l是物体的位移,不是路程。
F
m
M
l
W=Flcosα的理解
①F是恒力
②l是位移
F
l
③F和l必须同时存在
例如运动员用50N的力将蓝球水平扔出,蓝球在空飞了2m被截住,则运动员对蓝球做的功是100J。对吗?
G
F推
v
不做功
做功
G
v
不做功
F不做功
出手瞬间对球做功
④a是位移与力的夹角
α
起点相同时的夹角
【典例1 】如图表示物体在力F的作用下在水平面上发生了一段位移l,分别计算这三种情形下力F对物体做的功。设这三种情形下力F和位移l的大小都是一样的:F=10N,l=2m。角θ的大小如图所示。
F
l
l
l
二、正功和负功
W=Flcosα
①当α=π/2时,cosα=0,W=0。这表示力F的方向跟位移L的方向垂直,即力F不做功。
l
F1
②当0<α<π/2时, cosα>0,W>0,这表示力F1对物体做正功;
F2
③当π/2<α≤π时,cosα<0,W<0。这表示力F2对物体做负功。
④当α=0时,cosα=1,即W=Fl。
1. 正负不表示方向,也不表示大小。
负功的物理意义:
正功的物理意义:
表示该力是动力;
表示该力是阻力。
2.某力做多少负功,也可说成“物体克服该力做多少功”(取绝对值)。
v
f=5N
l=2m
A
B
F1
A
F2
B
如:-8J > 5J
正功和负功
思考:怎么比较功的大小?
比较绝对值
【典例2】一个质量m=150kg的雪橇,受到与水平方向成37°角的
斜向上方的拉力F=500N,在水平地面上移动的距离为5m,物体与
地面间的滑动摩擦力f=100N,cos 37°= 0.8。求
(1)各个力对物体所做的功
(2)各个力对物体做功的代数和
(3)物体所受的合力
(4)合力对物体做的功
三、总功的计算
三、总功的计算
1.分别求出每个力所做的功,然后求出所有功的代数和。即:
2.先求出物体所受的合力,然后再求出合力的功,即:
求总功的两种方法:
W总=F合Lcosα
【典例3】下列选项中,物体所受力F的大小相等,位移方向向右、大小相同。其中F做功最少的是( )
典例分析
【正确答案】D
典例分析
【典例4】如图所示,小明用与水平方向成角θ的轻绳拉木箱,绳中张力为F,沿水平地面向右移动了一段距离L,已知木箱与地面间的动摩擦因数为μ,木箱质量为m,木箱受到的( )
A.支持力做功为
B.重力做功为mgL
C.拉力做功为FL
D.滑动摩擦力做功为
【正确答案】D
情境引入
做同样的功
谁更快
【思考】起重机甲在60s内把1吨的货物匀速提高了5m,另一台起重机乙在30s内把1吨的货物匀速提高了5m。哪一台起重机做功快?如何比较它们做功的快慢?
提示:起重机乙做功快,做的功相同,用时少的做功快。
3.单位:在国际单位制中,功率的单位是瓦特,简称瓦,符号是W。
1W=1J/s,技术上常用千瓦(kW),1kW=1000W,1马力=735W
1.定义:力对物体做的功W,跟完成这些功所用时间t的比值叫功率.
4.物理意义:反映力对物体做功的快慢。
比值定义法
5.说明:功率是标量,计算功率时,一般不带正负号。
四、功率
2.定义式:
同时这个公式变形后给我们提供了一种求功的方法,即 W=pt.
即使是同一个力做功,做功的功率也可能是变化的,在一段时间内力对物体做功的功率,实际上是这段时间内力对物体做功的平均功率。
平均功率:描述在一段时间内做功的平均快慢
瞬时功率:表示在某一时刻做功的快慢
当 t 很短很短时,此式表示瞬时功率
当 t 表示一段时间时,此式表示平均功率
平均功率和瞬时功率
W=Flcosα
P=
t
W
P=Fvcosα
P=
t
Flcosα
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
v=
t
l
功率的另一种表达式
若v表示平均速度,则P表示平均功率
若v表示瞬时速度,则P表示瞬时功率
1.额定功率:是指机器正常工作时的最大输出功率,也就是机器铭
牌上的标称值。
2.实际功率:是指机器在工作中实际输出的功率。
额定功率和实际功率
(1)机器正常工作时实际功率总小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
(2)在日常生活中,某台机器的功率,或某物体做功的功率,实际上是指某个力对物体做功的功率。例如:汽车的功率就是汽车牵引力的功率,起重机吊起货物的功率就是钢绳拉力的功率。
1.功率是描述物体做功快慢程度的物理量
2.机械效率是描述机械做功时有效利用率的物理量
功率和机械效率区别
或
【典例4】如图所示为我国自行研制的新一代大型客机C919。假定其质量为m,起飞时在水平跑道上以加速度a做匀加速直线运动,受到的阻力大小为 ,当飞机速度为v时,则发动机输出的实际功率为( )
典例分析
【正确答案】B
A. B.
C. D.
【典例5】质量为m=10kg的物体放在粗糙的水平面上,物体与水平面间的动摩擦因数为 =0.25,现在大小为F=45N的水平拉力作用下从静止开始运动,通过一段s=4m的位移(g=10m/s2)求:
(1)该过程中拉力做的功;
(2)该过程拉力的平均功率和末状态的瞬时功率。
典例分析
【答案】(1)180J;(2)90W,180W;
【典例6】质量m=3kg的物体,在水平力F=6N的作用下,在光滑的水平面上从静止开始运动,运动时间t=3s,求:
(1)力F在t=3s内对物体做的功;
(2)力F在t=3s内对物体做功的平均功率;
(3)力F在3s末对物体做功的瞬时功率。
典例分析
【解析】a=F/m=2m/s2 ;l=v0t+1/2at2=9m,vt=v0+at=6m/s
(1)W=Fl=54J (2)P=W/t=18W (3)P1=FVt=36W
汽车启动
机车在行驶的过程中,发动机的最大功率等于额定功率。
P=F v
课堂引入
v
瞬时速度
功率
牵引力
机车的启动方式有两种:
1.以恒定功率P额启动;
2.在恒定的牵引力F作用下匀加速启动。
当F=F阻时,
a=0 ,v达到最大
保持 vm
匀速
v
F =
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
类型一:以恒定功率P额启动
F阻
F牵
F阻
F牵
vm
v—t 图象
加速阶段
的图象
匀速阶段
的图象
a减小的变加速运动
匀速运动
v0=0,P恒=P额
vm
v
t
0
1.F为变力时,发动机做的功只能用
W=Pt 计算,不能用W =Fl 计算。
总结:
2.达到最大速度的本质条件是:a=0
vm
v
t
0
说明:
3.达到最大速度时,有 P额=F阻vm
类型一:以恒定功率P额启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P =F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
类型二:以恒定加速度启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P =F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
类型二:以恒定加速度启动
机车做匀加速运动只能维持一段时间,当功率增大到额定功率时,匀加速运动结束,匀加速时间为:
t1=
P额
(ma+f阻)a
说明:
2.匀加速结束的条件是:P实=Pmax=P额
3.当匀加速结束时速度为v1,P额=Fv1=f阻Vm (其中F=ma+f阻)
t1
v1
v
t
0
vm
1.达到最大速度的本质条件:a=0
类型二:以恒定加速度启动
【典例1】(多选)按额定功率行驶的汽车,所受地面的阻力保持不变,则( )
A.汽车加速行驶时,牵引力不变,速度增大
B.汽车可以做匀加速运动
C.汽车加速行驶时,加速度逐渐减小,速度逐渐增大
D.汽车达到最大速度时,所受合力为零
典例分析
【正确答案】CD
【典例2】(多选)火车从车站开出做匀加速运动,若阻力与速度成正比,则( )
A.火车发动机的功率一定越来越大,牵引力越来越大
B.火车发动机的功率恒定不变,牵引力越来越小
C.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率这时应减小
D.当火车达到某一速率时,若要保持此速率做匀速运动,则发动机的功率一定跟此时速率的二次方成正比
【正确答案】ACD
典例分析
典例分析
【典例3】汽车的额定功率为60 kW,总质量为2×103 kg,运动中所受阻力恒为2 000 N.若汽车在额定功率下启动,求:
(1)当汽车的加速度是1 m/s2时的速度大小;
(2)汽车行驶的最大速度.
【答案】 (1)15 m/s (2)30 m/s
典例分析
【典例4】质量为m=4 t的机车,发动机的最大输出功率P=80 kW,运动阻力恒为Ff=2×103 N.
(1)若机车由静止开始以a=0.5 m/s2的加速度沿水平轨道做匀加速直线运动的过程中,求机车能达到的最大速度;
(2)若机车保持最大功率不变沿水平轨道行驶,求机车能达到的最大速度以及速度为10 m/s时机车的加速度.
【答案】 (1)20 m/s (2)40 m/s 1.5 m/s2
