2021-2022学年高中人教版(2019)必修第二册 7.2 万有引力定律 教学课件(47张PPT)
文档属性
| 名称 | 2021-2022学年高中人教版(2019)必修第二册 7.2 万有引力定律 教学课件(47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览








文档简介
(共47张PPT)
万有引力定律
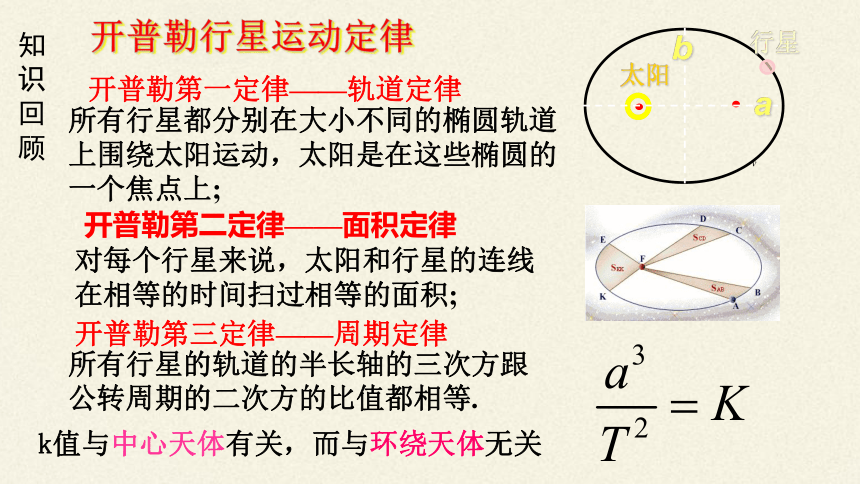
知识回顾
开普勒第一定律——轨道定律
所有行星都分别在大小不同的椭圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上;
开普勒第二定律——面积定律
对每个行星来说,太阳和行星的连线在相等的时间扫过相等的面积;
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
太阳
行星
b
v
a
k值与中心天体有关,而与环绕天体无关
开普勒行星运动定律
为什么天体运动轨迹是椭圆,而不是直线?
提出问题
一、行星与太阳间的引力
【思考】牛顿在前人研究的基础上认为任何方式改变速度都需要力,行星运动需要的力是哪个天体对它产生的力?
提示:太阳
太阳
行
太阳
行
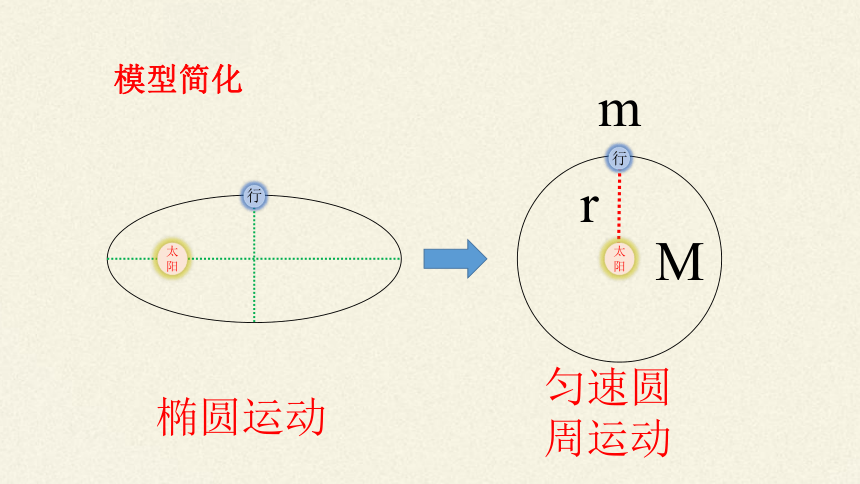
模型简化
椭圆运动
匀速圆
周运动
验证推理
(2)天文观测难以直接得到行星的速度v,但可以得到行星的公转周期T.
(1)设行星的质量为m,速度为v,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动的引力为多大?
(3)根据开普勒第三定律
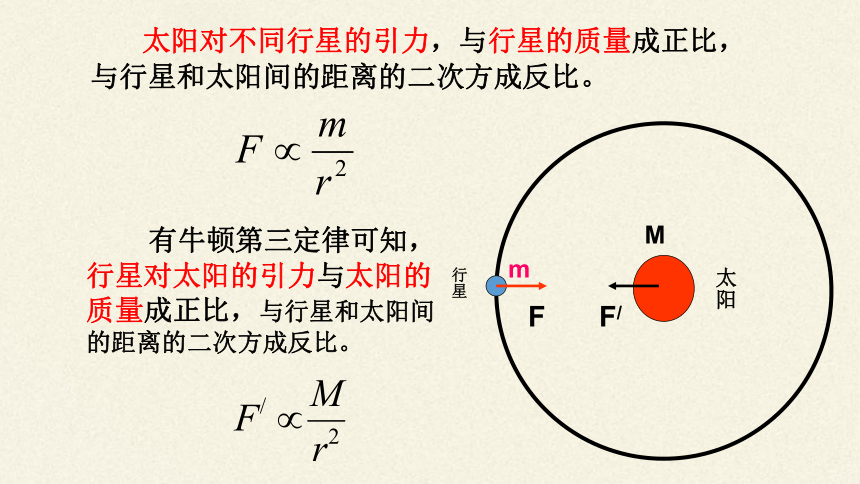
太阳对行星的引力
太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。
F
F/
行星
太阳
M
m
有牛顿第三定律可知,行星对太阳的引力与太阳的质量成正比,与行星和太阳间的距离的二次方成反比。
1.太阳对行星的引力大小:太阳对行星的引力F与行星
的质量m成正比,与行星与太阳的距离的二次方(r2)成
反比,即F∝____。
2.行星与太阳的引力:
(1)大小:行星与太阳的引力与太阳的质量m太成正比,
即F∝ ,写成等式就是F=________。
(2)方向:_____________。
(3)比例系数G:
关于G的数值解释符合科学实际的有_______。
①与太阳的质量无关。 ②与太阳的质量有关。
③与行星的质量无关。 ④与行星的质量有关。
⑤与太阳到行星的距离无关。
⑥与太阳到行星的距离有关。
沿二者的连线
①③⑤
太阳与行星间的引力
概括起来有
G比例系数,与太阳、行星的质量无关
则太阳与行星间的引力大小为
方向:沿着太阳和行星的连线
二、月—地检验
【思考】拉住月球使它围绕地球运动的力,与拉着苹果下落的力以及太阳对行星的力是否遵循相同的规律呢?
提示:遵循相同的规律
1.猜想:维持月球绕地球运动的力与使得苹果下落的力是同一种力,同样遵从“_________”的规律。
2.检验方法:
(1)物体在月球轨道上运动时的加速度:a=______。
(2)月球围绕地球做匀速圆周运动的加速度:a=_____。
平方反比
(3)对比结果:月球在轨道高度处的加速度近似等于_________________。
3.结论:地面物体受地球的引力,月球所受地球的引力,太阳与行星的引力,遵从相同的规律。
月球的向心加速度
三、万有引力定律
【思考】既然太阳与行星之间、地球与月球之间,以及地球与地面物体之间具有“与两个物体质量成正比,与它们之间的距离二次方成反比”的吸引力,是否任意两个物体之间都有这样的力呢?
提示:是
1.内容:自然界中任何两个物体都_________,引力的方
向在_____________,引力的大小与物体的质量m1和m2
的乘积成_____,与它们之间的距离r的二次方成_____。
2.公式:F=_______。
四、引力常量
1.测量者:_________。
2.数值:G=____________________。
相互吸引
它们的连线上
正比
反比
卡文迪什
6.67×10-11N·m2/kg2
四、万有引力常量
卡文迪什
卡文迪什扭秤实验
①数值: G=6.67×10-11 N·m2/kg2
②G值的物理含义:两个质量为1kg的物体相距1m时,它们之间万有引力为6.67×10-11 N
一、万有引力定律
1.万有引力定律的特性:
(1)普遍性:万有引力存在于宇宙中任何有质量的物体之间(天体间、地面物体间、微观粒子间)。
(2)相互性:两个物体间相互作用的引力是一对作用力和反作用力,符合力的相互作用。
(3)宏观性:天体间万有引力较大,它是支配天体运动的原因。地面物体间、微观粒子间的万有引力微小,不足以影响物体的运动,故常忽略不计。
(4)特殊性:两个物体间的万有引力只与它们本身的质量有关,与它们之间的距离有关,与所在空间的性质无关。
2.万有引力定律的适用条件:
(1)万有引力定律公式适用于质点之间的引力大小的计算。
(2)对于实际物体间的相互作用,当两个物体间的距离远远大于物体本身的大小(物体可视为质点)时也适用。
(3)两个质量分布均匀的球体间的引力大小可用万有引力定律公式求解,公式中的r为两球心之间的距离。
(4)一个质量分布均匀的球体与球外一质点之间的引力大小也可用万有引力定律公式求解,公式中的r为质点到球心之间的距离。
【思考·讨论】
李华认为两个人距离非常近时,根据公式F= 得出:r→0时,F→∞。李华同学的想法正确吗?为什么?(科学思维)
提示:不正确,因为两个人距离非常近时,不能视为质点,此公式不成立。
【典例示范】
要使两物体间的万有引力减小到原来的 ,下列办法不可采用的是( )
A.使两物体的质量各减少一半,距离不变
B.使两物体间的距离和两物体的质量都减为原来的
C.使两物体间的距离增为原来的2倍,质量不变
D.使其中一个物体的质量减小到原来的 ,距离不变
B
【素养训练】
1.(多选)对于质量为m1和质量为m2的两个物体间的万有引力的表达式F=G ,下列说法正确的是( )
A.公式中的G是引力常量,它是由实验得出的,而不是人为规定的
B.当两个物体间的距离r趋于零时,万有引力趋于无穷大
C.m1和m2所受引力大小总是相等的
D.两个物体间的引力总是大小相等、方向相反,是一对平衡力
AC
2.两个质量均匀的球体相距为r,它们之间的万有引力为1×10-8N,若它们的质量、距离都增加为原来的2倍,则它们之间的万有引力为( )
A.1×10-8N B.2×10-8N
C.4×10-8N D.8×10-8N
A
【补偿训练】
甲、乙两个质点间的万有引力大小为F,若甲质点的质量不变,乙质点的质量增大为原来的2倍,同时它们间的距离减为原来的 ,则甲、乙两个质点间的万有引力大小将变为( )
A. B.F C.4F D.8F
D
例:如图所示,两球的半径分别为r1和r2,两球质量均匀分布,大小分别为m1和m2,则两球间的万有引力大小为( )
A. B.
C. D.
变式:如图所示,两球的半径分别为r1和r2,且远小于r,而球质量均匀分布,大小分别为m1和m2,则两球间的万有引力大小为( )
A. B.
C. D.
练习:
如图所示,质量分布均匀的两球距离为d,现已知大球半径为R,质量为M,小球半径为r,质量为m,现在大球左侧挖去一半径为r、质量为M0的球,挖去后二者之间的万有引力大小?
处理方法:补偿法
两个重要推论
推论1:在匀质球层的空腔内的任意位置处,质点受到球壳万有引力的合力为零,即∑F=0
推论2:在匀质球体内部距球心r处,质点受到的万有引力就等于半径为r的球体的引力,即
二 万有引力与重力的关系
任务1 万有引力与重力的关系
1.万有引力和重力的关系:如图所示,设地球的质量为M,半径为R,A处物体的质量为m,则物体受到地球的吸引力为F,方向指向地心O,由万有引力公式得F=G 。引力F可分解为F1、F2两个分力,其中F1为物体随地球自转做圆周运动的向心力Fn,F2就是物体的重力mg。
2.重力与纬度的关系:地面上物体的重力随纬度的升高
而变大。
(1)赤道上:重力和向心力在一条直线上F=Fn+mg,
即G =mrω2+mg,所以mg=G -mrω2。
(2)地球两极处:向心力为零,所以mg=F=G 。
(3)其他位置:重力是万有引力的一个分力,重力的大小mg【典例示范1】如图所示,P、Q为质量相同的两质点,分别置于地球表面的不同纬度上,如果把地球看成一个均匀球体,P、Q两质点随地球自转做匀速圆周运动,则下列说法正确的是( )
A.P、Q做圆周运动的向心力大小相等
B.P、Q所受地球引力大小相等
C.P、Q做圆周运动的线速度大小相等
D.P所受地球引力大于Q所受地球引力
B
地球上空围绕地球做圆周运动的物体
R
h
当物体在距地面一定高度绕地心做匀速圆周运动时,地球自转对物体做圆周运动无影响,且此时地球对物体的万有引力就等于物体重力,引力提供物体做圆周运动的向心力,所以三者相等。
万有引力=重力提供向心力
物体处于完全失重状态
任务2 忽略地球自转的影响,万有引力与重力的关系
由于地球的自转角速度很小,故地球自转带来的影响很小,一般情况下认为:
(1)在地面附近:mg=G 。
(2)若距离地面的高度为h,则mg= (R为地球半径,g为离地面h高度处的重力加速度)。
例:
已知地球半径为R,试求位于离地面R/2高空的人造地球卫星所受到的重力加速度gR/2的大小?
变式训练:假设火星和地球都是球体,火星的质量M火和地球的质量M地之比M火/M地=p,火星的半径R火和地球的半径R地之比R火/R地=q,那么火星表面处的重力加速度g火和地球表面处的重力的加速度g地之比等于多少?
比值计算题
【典例示范2】假设有一星球的密度与地球相同,但它表面处的重力加速度是地球表面重力加速度的4倍,则该星球的质量是地球质量的( )
A. B.4倍 C.16倍 D.64倍
D
【素养训练】
1.2018年5月21日,嫦娥四号中继星“鹊桥”号成功发射,为嫦娥四号的着陆器和月球车提供地月中继通信支持。当“鹊桥”号在高空某处所受的引力为它在地面某处所受引力的一半,则“鹊桥”号离地面的高度与地球半径之比为 ( )
A.( +1)∶1 B.( -1)∶1
C. ∶1 D.1∶
B
2.设地球自转周期为T,质量为M,引力常量为G。假设地球可视为质量均匀分布的球体,半径为R。同一物体在南极和赤道水平面上静止时所受到的支持力之比为( )
A
【拓展例题】考查内容:万有引力与抛体运动综合问题
【典例示范】宇航员站在某一星球,从距离星球表面h高度处,以初速度v0沿水平方向抛出一个小球,经过时间t后小球落到星球表面,已知该星球的半径为R,引力常量为G,求:
(1)该星球表面重力加速度g的大小。
(2)该星球的质量。
【正确解答】(1)由平抛运动的知识知,在竖直方向小球做自由落体运动,h= gt2,
所以g= 。
(2)在星球表面,物体的重力和所受的万有引力相等。
故有:mg=G ,所以M=
答案:
【课堂回眸】
万有引力定律
知识回顾
开普勒第一定律——轨道定律
所有行星都分别在大小不同的椭圆轨道上围绕太阳运动,太阳是在这些椭圆的一个焦点上;
开普勒第二定律——面积定律
对每个行星来说,太阳和行星的连线在相等的时间扫过相等的面积;
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等.
太阳
行星
b
v
a
k值与中心天体有关,而与环绕天体无关
开普勒行星运动定律
为什么天体运动轨迹是椭圆,而不是直线?
提出问题
一、行星与太阳间的引力
【思考】牛顿在前人研究的基础上认为任何方式改变速度都需要力,行星运动需要的力是哪个天体对它产生的力?
提示:太阳
太阳
行
太阳
行
模型简化
椭圆运动
匀速圆
周运动
验证推理
(2)天文观测难以直接得到行星的速度v,但可以得到行星的公转周期T.
(1)设行星的质量为m,速度为v,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动的引力为多大?
(3)根据开普勒第三定律
太阳对行星的引力
太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。
F
F/
行星
太阳
M
m
有牛顿第三定律可知,行星对太阳的引力与太阳的质量成正比,与行星和太阳间的距离的二次方成反比。
1.太阳对行星的引力大小:太阳对行星的引力F与行星
的质量m成正比,与行星与太阳的距离的二次方(r2)成
反比,即F∝____。
2.行星与太阳的引力:
(1)大小:行星与太阳的引力与太阳的质量m太成正比,
即F∝ ,写成等式就是F=________。
(2)方向:_____________。
(3)比例系数G:
关于G的数值解释符合科学实际的有_______。
①与太阳的质量无关。 ②与太阳的质量有关。
③与行星的质量无关。 ④与行星的质量有关。
⑤与太阳到行星的距离无关。
⑥与太阳到行星的距离有关。
沿二者的连线
①③⑤
太阳与行星间的引力
概括起来有
G比例系数,与太阳、行星的质量无关
则太阳与行星间的引力大小为
方向:沿着太阳和行星的连线
二、月—地检验
【思考】拉住月球使它围绕地球运动的力,与拉着苹果下落的力以及太阳对行星的力是否遵循相同的规律呢?
提示:遵循相同的规律
1.猜想:维持月球绕地球运动的力与使得苹果下落的力是同一种力,同样遵从“_________”的规律。
2.检验方法:
(1)物体在月球轨道上运动时的加速度:a=______。
(2)月球围绕地球做匀速圆周运动的加速度:a=_____。
平方反比
(3)对比结果:月球在轨道高度处的加速度近似等于_________________。
3.结论:地面物体受地球的引力,月球所受地球的引力,太阳与行星的引力,遵从相同的规律。
月球的向心加速度
三、万有引力定律
【思考】既然太阳与行星之间、地球与月球之间,以及地球与地面物体之间具有“与两个物体质量成正比,与它们之间的距离二次方成反比”的吸引力,是否任意两个物体之间都有这样的力呢?
提示:是
1.内容:自然界中任何两个物体都_________,引力的方
向在_____________,引力的大小与物体的质量m1和m2
的乘积成_____,与它们之间的距离r的二次方成_____。
2.公式:F=_______。
四、引力常量
1.测量者:_________。
2.数值:G=____________________。
相互吸引
它们的连线上
正比
反比
卡文迪什
6.67×10-11N·m2/kg2
四、万有引力常量
卡文迪什
卡文迪什扭秤实验
①数值: G=6.67×10-11 N·m2/kg2
②G值的物理含义:两个质量为1kg的物体相距1m时,它们之间万有引力为6.67×10-11 N
一、万有引力定律
1.万有引力定律的特性:
(1)普遍性:万有引力存在于宇宙中任何有质量的物体之间(天体间、地面物体间、微观粒子间)。
(2)相互性:两个物体间相互作用的引力是一对作用力和反作用力,符合力的相互作用。
(3)宏观性:天体间万有引力较大,它是支配天体运动的原因。地面物体间、微观粒子间的万有引力微小,不足以影响物体的运动,故常忽略不计。
(4)特殊性:两个物体间的万有引力只与它们本身的质量有关,与它们之间的距离有关,与所在空间的性质无关。
2.万有引力定律的适用条件:
(1)万有引力定律公式适用于质点之间的引力大小的计算。
(2)对于实际物体间的相互作用,当两个物体间的距离远远大于物体本身的大小(物体可视为质点)时也适用。
(3)两个质量分布均匀的球体间的引力大小可用万有引力定律公式求解,公式中的r为两球心之间的距离。
(4)一个质量分布均匀的球体与球外一质点之间的引力大小也可用万有引力定律公式求解,公式中的r为质点到球心之间的距离。
【思考·讨论】
李华认为两个人距离非常近时,根据公式F= 得出:r→0时,F→∞。李华同学的想法正确吗?为什么?(科学思维)
提示:不正确,因为两个人距离非常近时,不能视为质点,此公式不成立。
【典例示范】
要使两物体间的万有引力减小到原来的 ,下列办法不可采用的是( )
A.使两物体的质量各减少一半,距离不变
B.使两物体间的距离和两物体的质量都减为原来的
C.使两物体间的距离增为原来的2倍,质量不变
D.使其中一个物体的质量减小到原来的 ,距离不变
B
【素养训练】
1.(多选)对于质量为m1和质量为m2的两个物体间的万有引力的表达式F=G ,下列说法正确的是( )
A.公式中的G是引力常量,它是由实验得出的,而不是人为规定的
B.当两个物体间的距离r趋于零时,万有引力趋于无穷大
C.m1和m2所受引力大小总是相等的
D.两个物体间的引力总是大小相等、方向相反,是一对平衡力
AC
2.两个质量均匀的球体相距为r,它们之间的万有引力为1×10-8N,若它们的质量、距离都增加为原来的2倍,则它们之间的万有引力为( )
A.1×10-8N B.2×10-8N
C.4×10-8N D.8×10-8N
A
【补偿训练】
甲、乙两个质点间的万有引力大小为F,若甲质点的质量不变,乙质点的质量增大为原来的2倍,同时它们间的距离减为原来的 ,则甲、乙两个质点间的万有引力大小将变为( )
A. B.F C.4F D.8F
D
例:如图所示,两球的半径分别为r1和r2,两球质量均匀分布,大小分别为m1和m2,则两球间的万有引力大小为( )
A. B.
C. D.
变式:如图所示,两球的半径分别为r1和r2,且远小于r,而球质量均匀分布,大小分别为m1和m2,则两球间的万有引力大小为( )
A. B.
C. D.
练习:
如图所示,质量分布均匀的两球距离为d,现已知大球半径为R,质量为M,小球半径为r,质量为m,现在大球左侧挖去一半径为r、质量为M0的球,挖去后二者之间的万有引力大小?
处理方法:补偿法
两个重要推论
推论1:在匀质球层的空腔内的任意位置处,质点受到球壳万有引力的合力为零,即∑F=0
推论2:在匀质球体内部距球心r处,质点受到的万有引力就等于半径为r的球体的引力,即
二 万有引力与重力的关系
任务1 万有引力与重力的关系
1.万有引力和重力的关系:如图所示,设地球的质量为M,半径为R,A处物体的质量为m,则物体受到地球的吸引力为F,方向指向地心O,由万有引力公式得F=G 。引力F可分解为F1、F2两个分力,其中F1为物体随地球自转做圆周运动的向心力Fn,F2就是物体的重力mg。
2.重力与纬度的关系:地面上物体的重力随纬度的升高
而变大。
(1)赤道上:重力和向心力在一条直线上F=Fn+mg,
即G =mrω2+mg,所以mg=G -mrω2。
(2)地球两极处:向心力为零,所以mg=F=G 。
(3)其他位置:重力是万有引力的一个分力,重力的大小mg
A.P、Q做圆周运动的向心力大小相等
B.P、Q所受地球引力大小相等
C.P、Q做圆周运动的线速度大小相等
D.P所受地球引力大于Q所受地球引力
B
地球上空围绕地球做圆周运动的物体
R
h
当物体在距地面一定高度绕地心做匀速圆周运动时,地球自转对物体做圆周运动无影响,且此时地球对物体的万有引力就等于物体重力,引力提供物体做圆周运动的向心力,所以三者相等。
万有引力=重力提供向心力
物体处于完全失重状态
任务2 忽略地球自转的影响,万有引力与重力的关系
由于地球的自转角速度很小,故地球自转带来的影响很小,一般情况下认为:
(1)在地面附近:mg=G 。
(2)若距离地面的高度为h,则mg= (R为地球半径,g为离地面h高度处的重力加速度)。
例:
已知地球半径为R,试求位于离地面R/2高空的人造地球卫星所受到的重力加速度gR/2的大小?
变式训练:假设火星和地球都是球体,火星的质量M火和地球的质量M地之比M火/M地=p,火星的半径R火和地球的半径R地之比R火/R地=q,那么火星表面处的重力加速度g火和地球表面处的重力的加速度g地之比等于多少?
比值计算题
【典例示范2】假设有一星球的密度与地球相同,但它表面处的重力加速度是地球表面重力加速度的4倍,则该星球的质量是地球质量的( )
A. B.4倍 C.16倍 D.64倍
D
【素养训练】
1.2018年5月21日,嫦娥四号中继星“鹊桥”号成功发射,为嫦娥四号的着陆器和月球车提供地月中继通信支持。当“鹊桥”号在高空某处所受的引力为它在地面某处所受引力的一半,则“鹊桥”号离地面的高度与地球半径之比为 ( )
A.( +1)∶1 B.( -1)∶1
C. ∶1 D.1∶
B
2.设地球自转周期为T,质量为M,引力常量为G。假设地球可视为质量均匀分布的球体,半径为R。同一物体在南极和赤道水平面上静止时所受到的支持力之比为( )
A
【拓展例题】考查内容:万有引力与抛体运动综合问题
【典例示范】宇航员站在某一星球,从距离星球表面h高度处,以初速度v0沿水平方向抛出一个小球,经过时间t后小球落到星球表面,已知该星球的半径为R,引力常量为G,求:
(1)该星球表面重力加速度g的大小。
(2)该星球的质量。
【正确解答】(1)由平抛运动的知识知,在竖直方向小球做自由落体运动,h= gt2,
所以g= 。
(2)在星球表面,物体的重力和所受的万有引力相等。
故有:mg=G ,所以M=
答案:
【课堂回眸】
