华东师大版数学八年级上册 13.3.1 等腰三角形的性质 课件(共19张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.3.1 等腰三角形的性质 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
§13.3.1
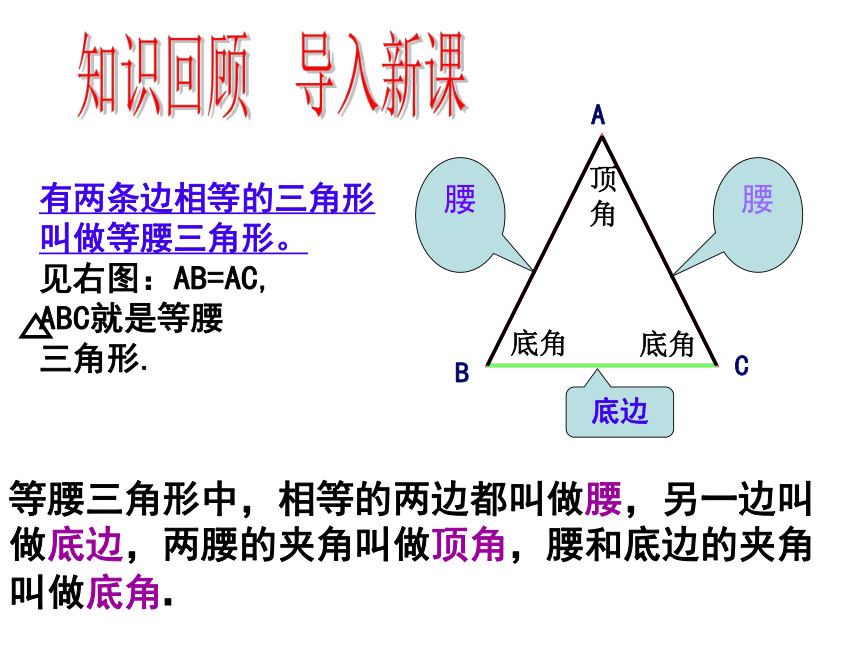
A
C
B
腰
腰
底边
底角
底角
顶角
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
有两条边相等的三角形叫做等腰三角形。
见右图:AB=AC, ABC就是等腰
三角形.
D
A
B
C
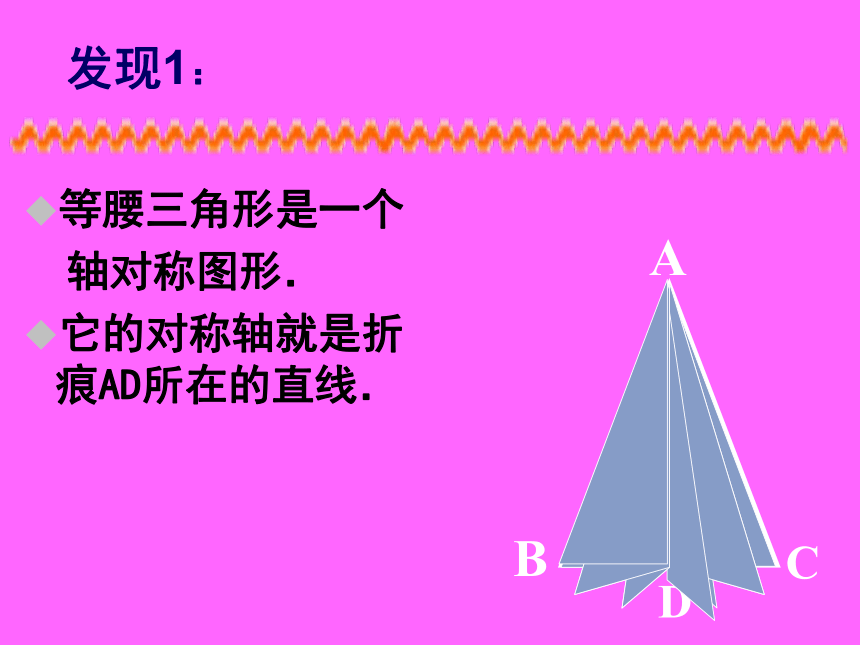
用半透明纸片剪出的等腰△ABC
将等腰三角形对折,使两腰 AB、AC重叠在一起,折痕为AD.
你能发现什么现象呢?
D
A
B
C
D
A
B
C
发现1:
等腰三角形是一个
轴对称图形.
它的对称轴就是折痕AD所在的直线.
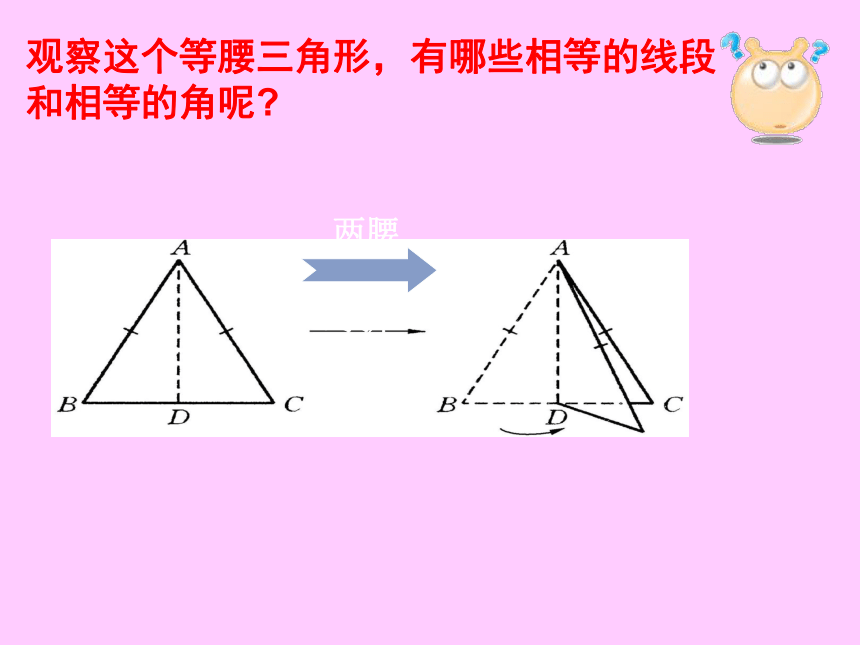
两腰
对折
观察这个等腰三角形,有哪些相等的线段 和相等的角呢
发现2:等腰三角形的两个底角相等。
C
B
A
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
方法一:作底边上的高AD
方法二:作底边上中线AD
方法三:作顶角的平分线AD
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
A
B
C
D
证明:作底边上的高AD
已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上的高AD
在RtΔBAD和RtΔCAD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt ΔBAD ≌ Rt ΔCAD(HL)
∴ ∠B=∠C(全等三角形的对应角相等)
性质1:等腰三角形的两个底角相等。
简写成:在同一个三角形中,等边对等角
A
B
C
D
已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上中线AD
在ΔBAD和ΔCAD中
AB=AC(已知)
BD=CD(辅助线作法)
AD=AD(公共边)
∴ ΔBAD ≌ΔCAD(SSS)
∴ ∠B=∠C(全等三角形的对应角相等)
性质1:等腰三角形的两个底角相等。
简写成:在同一个三角形中,等边对等角
A
B
C
D
1
2
已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作顶角的平分线AD
在ΔBAD和ΔCAD中
AB=AC(已知)
∠1=∠2(辅助线作法)
AD=AD(公共边)
∴ ΔBAD ≌ΔCAD(SAS)
∴ ∠B=∠C(全等三角形的对应角相等)
性质1:等腰三角形的两个底角相等。
A
B
C
D
1
2
简写成:在同一个三角形中,等边对等角.
C
B
D
A
性质1:
等腰三角形的两个底角相等.
简写成:在同一个三角形中,等边对等角.
符号语言:
在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C
(在同一个三角形中,等边对等角)
例1、已知:如图,在△ABC中,AB = AC,
∠ B = 80°.
求: ∠ A和 ∠C的度数。
A
B
C
变式:
已知:等腰三角形的一个内角为 50 °
求: 另两个角的度数.
70°,70°或40°,100°
30°,30°
2.等腰三角形一个角为40°,它的另外两个角为 ________________________
3.等腰三角形一个角为120°,它的另外两个角为_________________
1.等腰三角形一个底角为75°,它的另外两个角 为______________
75°, 30°
等腰三角形的底角可以是直角或钝角吗?为什么?
想一想
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称在同一个三角形中,等边对等角)
∵AB=AC
∴∠B=∠C
在△ABC中,
通过本节课的学习,谈谈自己的收获!
判断下列语句是否正确。
(1)有一个角是60°的等腰三角形,其它两个
内角也为60 °( ).
(2)等腰三角形的底角一定是锐角( ).
(3)钝角三角形不可能是等腰三角形 ( ).
×
同步练习
§13.3.1
A
C
B
腰
腰
底边
底角
底角
顶角
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
有两条边相等的三角形叫做等腰三角形。
见右图:AB=AC, ABC就是等腰
三角形.
D
A
B
C
用半透明纸片剪出的等腰△ABC
将等腰三角形对折,使两腰 AB、AC重叠在一起,折痕为AD.
你能发现什么现象呢?
D
A
B
C
D
A
B
C
发现1:
等腰三角形是一个
轴对称图形.
它的对称轴就是折痕AD所在的直线.
两腰
对折
观察这个等腰三角形,有哪些相等的线段 和相等的角呢
发现2:等腰三角形的两个底角相等。
C
B
A
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
方法一:作底边上的高AD
方法二:作底边上中线AD
方法三:作顶角的平分线AD
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
A
B
C
D
证明:作底边上的高AD
已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上的高AD
在RtΔBAD和RtΔCAD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt ΔBAD ≌ Rt ΔCAD(HL)
∴ ∠B=∠C(全等三角形的对应角相等)
性质1:等腰三角形的两个底角相等。
简写成:在同一个三角形中,等边对等角
A
B
C
D
已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上中线AD
在ΔBAD和ΔCAD中
AB=AC(已知)
BD=CD(辅助线作法)
AD=AD(公共边)
∴ ΔBAD ≌ΔCAD(SSS)
∴ ∠B=∠C(全等三角形的对应角相等)
性质1:等腰三角形的两个底角相等。
简写成:在同一个三角形中,等边对等角
A
B
C
D
1
2
已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作顶角的平分线AD
在ΔBAD和ΔCAD中
AB=AC(已知)
∠1=∠2(辅助线作法)
AD=AD(公共边)
∴ ΔBAD ≌ΔCAD(SAS)
∴ ∠B=∠C(全等三角形的对应角相等)
性质1:等腰三角形的两个底角相等。
A
B
C
D
1
2
简写成:在同一个三角形中,等边对等角.
C
B
D
A
性质1:
等腰三角形的两个底角相等.
简写成:在同一个三角形中,等边对等角.
符号语言:
在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C
(在同一个三角形中,等边对等角)
例1、已知:如图,在△ABC中,AB = AC,
∠ B = 80°.
求: ∠ A和 ∠C的度数。
A
B
C
变式:
已知:等腰三角形的一个内角为 50 °
求: 另两个角的度数.
70°,70°或40°,100°
30°,30°
2.等腰三角形一个角为40°,它的另外两个角为 ________________________
3.等腰三角形一个角为120°,它的另外两个角为_________________
1.等腰三角形一个底角为75°,它的另外两个角 为______________
75°, 30°
等腰三角形的底角可以是直角或钝角吗?为什么?
想一想
等腰三角形的性质
文字叙述
几何语言
等腰三角形的两底角相等(简称在同一个三角形中,等边对等角)
∵AB=AC
∴∠B=∠C
在△ABC中,
通过本节课的学习,谈谈自己的收获!
判断下列语句是否正确。
(1)有一个角是60°的等腰三角形,其它两个
内角也为60 °( ).
(2)等腰三角形的底角一定是锐角( ).
(3)钝角三角形不可能是等腰三角形 ( ).
×
同步练习
