华东师大版数学八年级上册 11.1.1 平方根 课件(共61张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 11.1.1 平方根 课件(共61张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 09:21:02 | ||
图片预览










文档简介
(共61张PPT)
平方根
回顾
1、从小学到初中我们学过哪些基本运算
加法:3 + 4 =7
减法: 7 4 =3
乘法:4 × 6 =24
除法:24 ÷ 4 =6
逆运算
逆运算
将9逆运算回去得到原来的数字3或-3
逆运算
平方: = 9
= 9
回顾
1、从小学到初中我们学过哪些基本运算
将9逆运算回去得到原来的数字3或-3
将乘方运算的结果逆运算回去得到原来的数字的过程。
开平方
开平方
平方: = 9
= 9
逆运算
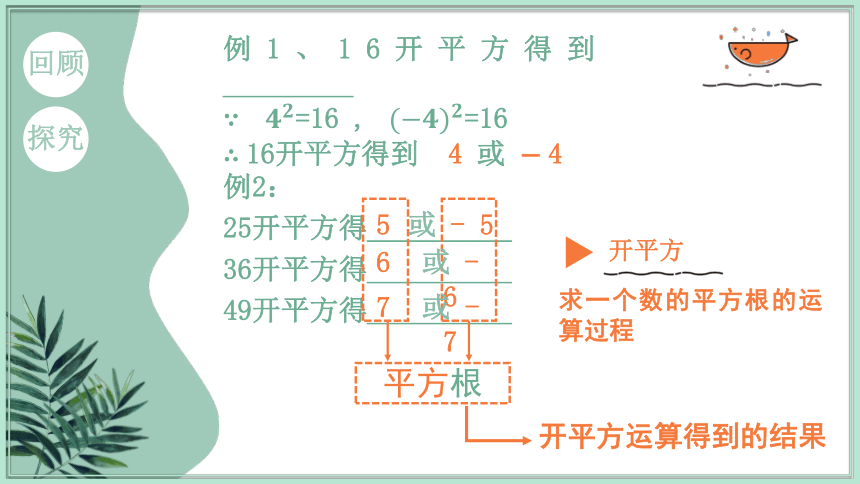
例1、16开平方得到_________
∵ =16 , =16
∴ 16开平方得到 4 或 4
例2:
25开平方得__________
36开平方得__________
49开平方得__________
平方根
开平方运算得到的结果
回顾
探究
5
或 - 5
6
或 - 6
7
或 - 7
求一个数的平方根的运算过程
开平方
若=a,则x是a的平方根
平方根
【求一个数的平方根解题思路:】
求某数的平方根 谁的平方等于该数
转化
求25的平方根
转化
求谁的平方等于25
5或- 5的平方等于25
转化
25的平方根是5或- 5
回顾
探究
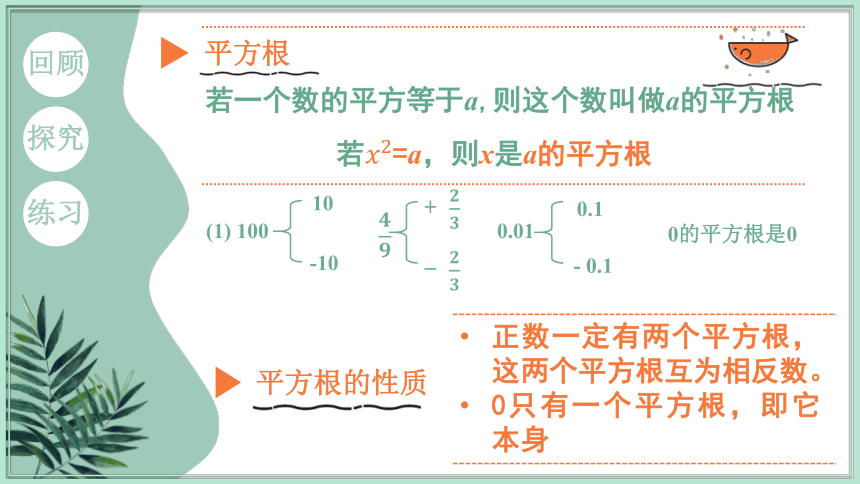
若一个数的平方等于a,则这个数叫做a的平方根
例:求25的平方根
解:∵ =25 且= 25
∴ 5或- 5是25的平方根
回顾
探究
若=a,则x是a的平方根
平方根
【求一个数的平方根解题思路:】
求某数的平方根 谁的平方等于该数
转化
若一个数的平方等于a,则这个数叫做a的平方根
【练1】(1)求100的平方根
解:∵= 100 且= 100
∴ 10或- 10是100的平方根
回顾
探究
练习
(2)求0的平方根
解:∵ = 0
∴ 0的平方根是0
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
【练1】(3)求的平方根
解:∵ = 且=
∴ 或 是 的平方根
回顾
探究
练习
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
【练1】
回顾
探究
练习
(4)求0.01的平方根
解:∵ (±= 0.01
∴ 0.01的平方根是±
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
【练2】
回顾
探究
练习
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
口答:
(1)81的平方根是什么
(2) 0的平方根是什么
(3)的平方根是什么
正数的平方根有什么特点?0的平方根是多少?
若=a,则x是a的平方根
回顾
探究
练习
(1) 100
10
-10
0的平方根是0
平方根的性质
正数一定有两个平方根,这两个平方根互为相反数。
0只有一个平方根,即它本身
平方根
若一个数的平方等于a,则这个数叫做a的平方根
+
-
0.01
0.1
- 0.1
回顾
探究
练方根的性质
正数一定有两个平方根,这两个平方根互为相反数。
0只有一个平方根,即它本身
【思考】负数是否有平方根
在实数范围内,一个数的平方不可能等于负数,所以负数没有平方根
∵ =a,则x是a平方根
负数没有平方根
回顾
探究
练习
【练习】(1)下面哪个数没有平方根
A、-81 B、0 C、
(2)下面哪个数有两个平方根
A、-36 B、0.0001 C、
(3)= 4,则4的平方根是_______
= 36,则36的平方根是_______
= 49,则49的平方根是_______
【练习】2.下列各数有平方根吗?说明理由。
判断一个数有没有平方根,只要看这个数的符号。
当这个数为正数时,它有两个平方根;
当这个数为0时,它有一个平方根0;
当这个数为负数时,它没有平方根。
回顾
探究
练习
(1)- 4 (2)
(3) (4)0
(5) (6)| 3 |
(7)3.14- (8)+1
【练习】3.判断 。
回顾
探究
练习
(1)5是25的一个平方根;
(2)25的平方根是5;
(3)-9的平方根是 - 3;
(4)的平方根是±2 ;
(5)若= 16,则x = 4
回顾
探究
练习
1
4
9
16
25
36
完全平方数
49
64
81
100
121
144
=
=
=
=
=
=
169
196
225
256
289
324
=
=
=
=
=
=
361
400
625
=
=
=
=
=
=
=
=
=
回顾
探究
练习
1
4
9
16
25
36
=
=
=
=
=
=
49
64
81
100
121
144
=
=
=
=
=
=
169
196
225
256
289
324
=
=
=
=
=
=
361
400
625
=
=
=
完全平方数
回顾
探究
练习
【随堂练习】
(1)下面各数有平方根吗?若有,求出他们的平方根;若没有,说明理由
A、-64 B、 C、
(2)196的平方根是_______
0 . 0049的平方根是________
若某数的平方根是±4,则该数是_______
(3)若m-4没有平方根,则 | m-5 |=_____
若3x+4的平方根为±1,则x=_______
算术平方根
讲授:秦海霞
年级:八年级
回顾
1、什么是平方根?
若一个数的平方等于a,则这个数叫做a的平方根
若=a,则x是a的平方根
2、平方根有哪些性质?
正数一定有两个平方根,这两个平方根互为相反数。
0只有一个平方根,即它本身
负数没有平方根
回顾
探究
【探究】小明要裁剪一块25平方分米的正方
形画布作画,请问这块正方形画布边长是多少?
求25的
平方根
正的
25的平方根是5或-5
25
平方根
5
-5
算术平方根
正的
几何意义
回顾
探究
算术平方根
正的
几何意义
任何正数都有且只有一个算术平方根
0的算术平方根是0
负数没有算术平方根
性质
回顾
探究
【算术平方根的表示方法】
算术平方根的运算符号:或
读作:根号或二次根号
表示的意义:求一个数的算术平方根
求a(a>0)的算术平方根:或 (a叫做被开方数)
[例 1] (1)9的算术平方根是_____
(2)36的算术平方根表示为_____
(3) =_____
(4)=____
回顾
探究
【算术平方根的表示方法】
算术平方根的运算符号:或
读作:根号或二次根号
表示的意义:求一个数的算术平方根
求a(a≥0)的算术平方根:或(a叫做被开方数)
【平方根的表示方法】
运算符号:± 或 ±
读作:正负根号
表示的意义:求一个数的平方根
求a(a≥0)的平方根:± 或 ±(a叫做被开方数)
回顾
探究
【算术平方根的表示方法】
在实数范围内,若或有意义,则a≥0
【辨析
练习
相同: 中的a都是非负数,即a≥0
不同:
表示a的平方根,是求平方根的运算符号
表示a的算术平方根(正的平方根),是求算术平方根
的运算符号
表示a的负的平方根
回顾
探究
【算术平方根的表示方法】
在实数范围内,若或有意义,则a≥0
[例 2] 以下求算术平方根的运算在实数范围内成立的有几个?
、 、、、、、
[例 3] (1)求64的算术平方根
_________________
(2)_____的算术平方根是6
(3) =_____,表示_________________
练习
回顾
探究
[例 4] 表示“81的算术平方根是9”的正确的是( )
A、±=± B、 =
C、 = D、 =±
[例 5] (1)表示 _________________
(2)±表示________________
(3)-表示_________________
(4)表示________________,等于_____
(5)表示_______________,等于_____
练方根专项练习
讲授:秦海霞
年级:八年级
回顾
平方根的定义
算术平方根的定义
平方根的性质
算术平方根的性质
【基础训练】
练
【基础训练之求平方根】
(1)求下列各数的平方根:
(1) 1.69 (2)2 (3)232 (4)
(2)将下列各数开平方
(1) 2 (2) (3)
练
【基础训练之求算术平方根】
求下列各数的算术平方根。
(1) 196 (2) (3) 0.04 (4) (5)
求算术平方根及平方根时,被开方数要化简;
题中注意的算术平方根及的意义不同.
练
(1)144的算术平方根是( )
A、-12 B、+12 C、± 12 D、
(2)下列说法正确的是( )
A、一个数的平方等于1,那么这个数就是1
B、± 6是36的算术平方根
C、7是的算术平方根
D、4是8的算术平方根
【基础训练之平方根与算术平方根】
(3)下列说法正确的是( )
A、9是81的算术平方根:±=9
B、± 15是225的平方根:= ± 15
C、11是的算术平方根: =11
D、-2是4的负的平方根:= -2
练
【基础训练之平方根与算术平方根】
练
【平方根拓展练习】
(1)计算- 的值为( )
A、- B、 C、± D、
(2)计算 =3,则a的值为( )
A、3 B、±3 C、± D、-3
【拓展训练】
例
【平方根拓展练习】
(1)的平方根是______
(2)的算术平方根是______
看清题目表述
(3)的平方根是______
(4)的算术平方根是______
(5)的平方根是______
(6)的算术平方根是______
的平方根(算术平方根)
a 的平方根(算术平方根)
练
【基础训练之求平方根】
一、选择题
(1)下列四个数中最大的一个数是( )
A、2 B、 C、0 D、-2
(2)下列各组数中互为相反数的一组是( )
A、-2与 B 、 -2与
C、 -2与- D、| -2|与2
练
【基础训练之求平方根】
一、选择题
(3)下列各数中:0、、、 | - | 、 、-(-2)其中有平方根的有( )
A、3个 B、 C、5个 D、6个
(4)设=a,则下列结论正确的是( )
A、4.5C、 5.5练
【基础训练之求平方根】
一、选择题
(5)下列说法正确的是( )
A、若| a | = | b | ,则a =b
B、若 a C、若 = ,则a =b
D、若 = ,则| a | = | b |
练
【基础训练之求平方根】
一、选择题
(6)如果实数a满足等式| a | =- a,那么实数a是( )
A、正数 B、 C、有理数 D、非正数
(7)已知实数在数轴上所对应的点的位置如图,下列结论错误的是( )
A、 | a |<1< | b | B 、 1 <- a < b
C、 1< | a |< | b | D、- b0
1
a
-1
b
例
【平方根拓展练习】
(1)4的算术平方根是______
带字母的算术平方根
哪个非负数平方是4
=4
=
==
| 2|
算术平方根一定是非负的,当不确定字母的非负性时,使用绝对值确保结果的非负。
例
【平方根拓展练习】
(1)的平方根是______
| |
第一步:化简| |
第二步:题目转化为求| |的平方根
第三步:| |的平方根是
练
【平方根拓展练习】
(3)计算 =______
=______
=______
凑平方
【能力提升】
练
求下列各式中x的值(解方程)
(1) =6 (2) 64=25 (3)=9
(1)解:
∵=6
∴ x是6的平方根
∴ x=±
(2)解:
∵64=25
=
∴ x是的平方根
∴ x=±
(3)解:
∵=9
∴ 是9的平方根
∴ =±3
∴ x=4或 x=-2
【能力提升】
例
【能力提升之根据平方根求原数】
已知2a+1的平方根是± 3,5a+2b-2的算术平方根是4,求3a-4b的算术平方根。
2a+1
5a+2b-2
3a-4b
原数
平方根
±3
4
算术平方根
?
例
已知2a+1的平方根是± 3,5a+2b-2的算术平方根是4,求3a-4b的算术平方根。
【能力提升之根据平方根求原数】
练
已知一个正数x的一个平方根3a 5是,另一个平方根是1-2a ,则 x=_______
正数的平方根互为相反数
解 由题得 (3a 5)+( 1-2a )=0
a= 4
∴ 3a 5 =7
∴ x==49
【能力提升之根据平方根求原数】
练
已知一个数x的算术平方根2a 6,平方根是±(a-2) ,求x
正数的算术平方根=正的平方根
解 a-2是算术平方根
则a-2= 2a 6
解得 a=4
∴ a-2 =2
∴ x==4
【能力提升之根据平方根求原数】
解 (a-2) 是算术平方根
则 (a-2) = 2a 6
解得 a=
∴ 2a 6 =
>0(符合题意)
<0(不符合题意)
∴ 综上所述,该数是4
1
2
练
【基础训练之求平方根】
一、选择题
(1)下列四个数中最大的一个数是( )
A、2 B、 C、0 D、-2
(2)下列各组数中互为相反数的一组是( )
A、-2与 B 、 -2与
C、 -2与- D、| -2|与2
练
【基础训练之求平方根】
一、选择题
(3)下列各数中: 0、、、 | - | 、 、-(-2)其中有平方根的有( )
A、3个 B、 C、5个 D、6个
(4)设=a,则下列结论正确的是( )
A、4.5C、 5.5练
【基础训练之求平方根】
一、选择题
(5)下列说法正确的是( )
A、若| a | = | b | ,则a =b
B、若 a C、若 = ,则a =b
D、若 = ,则a =b
练
【基础训练之求实数】
一、选择题
(6)如果实数a满足等式| a | =- a,那么实数a是( )
A、正数
B、
C、有理数
D、非正数
练
【基础训练之求实数】
一、选择题
(7)已知实数在数轴上所对应的点的位置如图,下列结论错误的是( )
A、 | a |<1< | b | B 、 1 <- a < b
C、 1< | a |< | b | D、- b0
1
a
-1
b
练
【基础训练之求平方根立方根】
二、填空题
(8) | -5 |+ =______
(9)在实数 - 、、2.236、 、0.303003000```、2- 、1- 、 中,无理数有_____个
练
【基础训练之求平方根和立方根】
二、填空题
(10)下列说法正确的是_____
正数的立方根有两个,他们互为相反数
的平方根是±3
对于任意的实数都有 = a
练
【基础训练之求实数】
二、填空题
(11)一个正数的平方根分别是3x-2和2x+6,则x=______
(12)若x,y为实数,且|x-2|+=0,则 =______
(13)求下列各数的平方根
练
【基础训练之求平方根】
二、填空题
(14)计算;
± -
练
【基础训练之求平方根和立方根】
二、填空题
(15)求下列各式中x的值
169=100 +27=0
练
【拓展之求平方根】
二、填空题
(16)已知x-2的平方根是±4, 2x-y+12的立方根是4,求x+y的算术平方根
平方根
回顾
1、从小学到初中我们学过哪些基本运算
加法:3 + 4 =7
减法: 7 4 =3
乘法:4 × 6 =24
除法:24 ÷ 4 =6
逆运算
逆运算
将9逆运算回去得到原来的数字3或-3
逆运算
平方: = 9
= 9
回顾
1、从小学到初中我们学过哪些基本运算
将9逆运算回去得到原来的数字3或-3
将乘方运算的结果逆运算回去得到原来的数字的过程。
开平方
开平方
平方: = 9
= 9
逆运算
例1、16开平方得到_________
∵ =16 , =16
∴ 16开平方得到 4 或 4
例2:
25开平方得__________
36开平方得__________
49开平方得__________
平方根
开平方运算得到的结果
回顾
探究
5
或 - 5
6
或 - 6
7
或 - 7
求一个数的平方根的运算过程
开平方
若=a,则x是a的平方根
平方根
【求一个数的平方根解题思路:】
求某数的平方根 谁的平方等于该数
转化
求25的平方根
转化
求谁的平方等于25
5或- 5的平方等于25
转化
25的平方根是5或- 5
回顾
探究
若一个数的平方等于a,则这个数叫做a的平方根
例:求25的平方根
解:∵ =25 且= 25
∴ 5或- 5是25的平方根
回顾
探究
若=a,则x是a的平方根
平方根
【求一个数的平方根解题思路:】
求某数的平方根 谁的平方等于该数
转化
若一个数的平方等于a,则这个数叫做a的平方根
【练1】(1)求100的平方根
解:∵= 100 且= 100
∴ 10或- 10是100的平方根
回顾
探究
练习
(2)求0的平方根
解:∵ = 0
∴ 0的平方根是0
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
【练1】(3)求的平方根
解:∵ = 且=
∴ 或 是 的平方根
回顾
探究
练习
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
【练1】
回顾
探究
练习
(4)求0.01的平方根
解:∵ (±= 0.01
∴ 0.01的平方根是±
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
【练2】
回顾
探究
练习
若=a,则x是a的平方根
平方根
若一个数的平方等于a,则这个数叫做a的平方根
口答:
(1)81的平方根是什么
(2) 0的平方根是什么
(3)的平方根是什么
正数的平方根有什么特点?0的平方根是多少?
若=a,则x是a的平方根
回顾
探究
练习
(1) 100
10
-10
0的平方根是0
平方根的性质
正数一定有两个平方根,这两个平方根互为相反数。
0只有一个平方根,即它本身
平方根
若一个数的平方等于a,则这个数叫做a的平方根
+
-
0.01
0.1
- 0.1
回顾
探究
练方根的性质
正数一定有两个平方根,这两个平方根互为相反数。
0只有一个平方根,即它本身
【思考】负数是否有平方根
在实数范围内,一个数的平方不可能等于负数,所以负数没有平方根
∵ =a,则x是a平方根
负数没有平方根
回顾
探究
练习
【练习】(1)下面哪个数没有平方根
A、-81 B、0 C、
(2)下面哪个数有两个平方根
A、-36 B、0.0001 C、
(3)= 4,则4的平方根是_______
= 36,则36的平方根是_______
= 49,则49的平方根是_______
【练习】2.下列各数有平方根吗?说明理由。
判断一个数有没有平方根,只要看这个数的符号。
当这个数为正数时,它有两个平方根;
当这个数为0时,它有一个平方根0;
当这个数为负数时,它没有平方根。
回顾
探究
练习
(1)- 4 (2)
(3) (4)0
(5) (6)| 3 |
(7)3.14- (8)+1
【练习】3.判断 。
回顾
探究
练习
(1)5是25的一个平方根;
(2)25的平方根是5;
(3)-9的平方根是 - 3;
(4)的平方根是±2 ;
(5)若= 16,则x = 4
回顾
探究
练习
1
4
9
16
25
36
完全平方数
49
64
81
100
121
144
=
=
=
=
=
=
169
196
225
256
289
324
=
=
=
=
=
=
361
400
625
=
=
=
=
=
=
=
=
=
回顾
探究
练习
1
4
9
16
25
36
=
=
=
=
=
=
49
64
81
100
121
144
=
=
=
=
=
=
169
196
225
256
289
324
=
=
=
=
=
=
361
400
625
=
=
=
完全平方数
回顾
探究
练习
【随堂练习】
(1)下面各数有平方根吗?若有,求出他们的平方根;若没有,说明理由
A、-64 B、 C、
(2)196的平方根是_______
0 . 0049的平方根是________
若某数的平方根是±4,则该数是_______
(3)若m-4没有平方根,则 | m-5 |=_____
若3x+4的平方根为±1,则x=_______
算术平方根
讲授:秦海霞
年级:八年级
回顾
1、什么是平方根?
若一个数的平方等于a,则这个数叫做a的平方根
若=a,则x是a的平方根
2、平方根有哪些性质?
正数一定有两个平方根,这两个平方根互为相反数。
0只有一个平方根,即它本身
负数没有平方根
回顾
探究
【探究】小明要裁剪一块25平方分米的正方
形画布作画,请问这块正方形画布边长是多少?
求25的
平方根
正的
25的平方根是5或-5
25
平方根
5
-5
算术平方根
正的
几何意义
回顾
探究
算术平方根
正的
几何意义
任何正数都有且只有一个算术平方根
0的算术平方根是0
负数没有算术平方根
性质
回顾
探究
【算术平方根的表示方法】
算术平方根的运算符号:或
读作:根号或二次根号
表示的意义:求一个数的算术平方根
求a(a>0)的算术平方根:或 (a叫做被开方数)
[例 1] (1)9的算术平方根是_____
(2)36的算术平方根表示为_____
(3) =_____
(4)=____
回顾
探究
【算术平方根的表示方法】
算术平方根的运算符号:或
读作:根号或二次根号
表示的意义:求一个数的算术平方根
求a(a≥0)的算术平方根:或(a叫做被开方数)
【平方根的表示方法】
运算符号:± 或 ±
读作:正负根号
表示的意义:求一个数的平方根
求a(a≥0)的平方根:± 或 ±(a叫做被开方数)
回顾
探究
【算术平方根的表示方法】
在实数范围内,若或有意义,则a≥0
【辨析
练习
相同: 中的a都是非负数,即a≥0
不同:
表示a的平方根,是求平方根的运算符号
表示a的算术平方根(正的平方根),是求算术平方根
的运算符号
表示a的负的平方根
回顾
探究
【算术平方根的表示方法】
在实数范围内,若或有意义,则a≥0
[例 2] 以下求算术平方根的运算在实数范围内成立的有几个?
、 、、、、、
[例 3] (1)求64的算术平方根
_________________
(2)_____的算术平方根是6
(3) =_____,表示_________________
练习
回顾
探究
[例 4] 表示“81的算术平方根是9”的正确的是( )
A、±=± B、 =
C、 = D、 =±
[例 5] (1)表示 _________________
(2)±表示________________
(3)-表示_________________
(4)表示________________,等于_____
(5)表示_______________,等于_____
练方根专项练习
讲授:秦海霞
年级:八年级
回顾
平方根的定义
算术平方根的定义
平方根的性质
算术平方根的性质
【基础训练】
练
【基础训练之求平方根】
(1)求下列各数的平方根:
(1) 1.69 (2)2 (3)232 (4)
(2)将下列各数开平方
(1) 2 (2) (3)
练
【基础训练之求算术平方根】
求下列各数的算术平方根。
(1) 196 (2) (3) 0.04 (4) (5)
求算术平方根及平方根时,被开方数要化简;
题中注意的算术平方根及的意义不同.
练
(1)144的算术平方根是( )
A、-12 B、+12 C、± 12 D、
(2)下列说法正确的是( )
A、一个数的平方等于1,那么这个数就是1
B、± 6是36的算术平方根
C、7是的算术平方根
D、4是8的算术平方根
【基础训练之平方根与算术平方根】
(3)下列说法正确的是( )
A、9是81的算术平方根:±=9
B、± 15是225的平方根:= ± 15
C、11是的算术平方根: =11
D、-2是4的负的平方根:= -2
练
【基础训练之平方根与算术平方根】
练
【平方根拓展练习】
(1)计算- 的值为( )
A、- B、 C、± D、
(2)计算 =3,则a的值为( )
A、3 B、±3 C、± D、-3
【拓展训练】
例
【平方根拓展练习】
(1)的平方根是______
(2)的算术平方根是______
看清题目表述
(3)的平方根是______
(4)的算术平方根是______
(5)的平方根是______
(6)的算术平方根是______
的平方根(算术平方根)
a 的平方根(算术平方根)
练
【基础训练之求平方根】
一、选择题
(1)下列四个数中最大的一个数是( )
A、2 B、 C、0 D、-2
(2)下列各组数中互为相反数的一组是( )
A、-2与 B 、 -2与
C、 -2与- D、| -2|与2
练
【基础训练之求平方根】
一、选择题
(3)下列各数中:0、、、 | - | 、 、-(-2)其中有平方根的有( )
A、3个 B、 C、5个 D、6个
(4)设=a,则下列结论正确的是( )
A、4.5
【基础训练之求平方根】
一、选择题
(5)下列说法正确的是( )
A、若| a | = | b | ,则a =b
B、若 a C、若 = ,则a =b
D、若 = ,则| a | = | b |
练
【基础训练之求平方根】
一、选择题
(6)如果实数a满足等式| a | =- a,那么实数a是( )
A、正数 B、 C、有理数 D、非正数
(7)已知实数在数轴上所对应的点的位置如图,下列结论错误的是( )
A、 | a |<1< | b | B 、 1 <- a < b
C、 1< | a |< | b | D、- b
1
a
-1
b
例
【平方根拓展练习】
(1)4的算术平方根是______
带字母的算术平方根
哪个非负数平方是4
=4
=
==
| 2|
算术平方根一定是非负的,当不确定字母的非负性时,使用绝对值确保结果的非负。
例
【平方根拓展练习】
(1)的平方根是______
| |
第一步:化简| |
第二步:题目转化为求| |的平方根
第三步:| |的平方根是
练
【平方根拓展练习】
(3)计算 =______
=______
=______
凑平方
【能力提升】
练
求下列各式中x的值(解方程)
(1) =6 (2) 64=25 (3)=9
(1)解:
∵=6
∴ x是6的平方根
∴ x=±
(2)解:
∵64=25
=
∴ x是的平方根
∴ x=±
(3)解:
∵=9
∴ 是9的平方根
∴ =±3
∴ x=4或 x=-2
【能力提升】
例
【能力提升之根据平方根求原数】
已知2a+1的平方根是± 3,5a+2b-2的算术平方根是4,求3a-4b的算术平方根。
2a+1
5a+2b-2
3a-4b
原数
平方根
±3
4
算术平方根
?
例
已知2a+1的平方根是± 3,5a+2b-2的算术平方根是4,求3a-4b的算术平方根。
【能力提升之根据平方根求原数】
练
已知一个正数x的一个平方根3a 5是,另一个平方根是1-2a ,则 x=_______
正数的平方根互为相反数
解 由题得 (3a 5)+( 1-2a )=0
a= 4
∴ 3a 5 =7
∴ x==49
【能力提升之根据平方根求原数】
练
已知一个数x的算术平方根2a 6,平方根是±(a-2) ,求x
正数的算术平方根=正的平方根
解 a-2是算术平方根
则a-2= 2a 6
解得 a=4
∴ a-2 =2
∴ x==4
【能力提升之根据平方根求原数】
解 (a-2) 是算术平方根
则 (a-2) = 2a 6
解得 a=
∴ 2a 6 =
>0(符合题意)
<0(不符合题意)
∴ 综上所述,该数是4
1
2
练
【基础训练之求平方根】
一、选择题
(1)下列四个数中最大的一个数是( )
A、2 B、 C、0 D、-2
(2)下列各组数中互为相反数的一组是( )
A、-2与 B 、 -2与
C、 -2与- D、| -2|与2
练
【基础训练之求平方根】
一、选择题
(3)下列各数中: 0、、、 | - | 、 、-(-2)其中有平方根的有( )
A、3个 B、 C、5个 D、6个
(4)设=a,则下列结论正确的是( )
A、4.5
【基础训练之求平方根】
一、选择题
(5)下列说法正确的是( )
A、若| a | = | b | ,则a =b
B、若 a C、若 = ,则a =b
D、若 = ,则a =b
练
【基础训练之求实数】
一、选择题
(6)如果实数a满足等式| a | =- a,那么实数a是( )
A、正数
B、
C、有理数
D、非正数
练
【基础训练之求实数】
一、选择题
(7)已知实数在数轴上所对应的点的位置如图,下列结论错误的是( )
A、 | a |<1< | b | B 、 1 <- a < b
C、 1< | a |< | b | D、- b
1
a
-1
b
练
【基础训练之求平方根立方根】
二、填空题
(8) | -5 |+ =______
(9)在实数 - 、、2.236、 、0.303003000```、2- 、1- 、 中,无理数有_____个
练
【基础训练之求平方根和立方根】
二、填空题
(10)下列说法正确的是_____
正数的立方根有两个,他们互为相反数
的平方根是±3
对于任意的实数都有 = a
练
【基础训练之求实数】
二、填空题
(11)一个正数的平方根分别是3x-2和2x+6,则x=______
(12)若x,y为实数,且|x-2|+=0,则 =______
(13)求下列各数的平方根
练
【基础训练之求平方根】
二、填空题
(14)计算;
± -
练
【基础训练之求平方根和立方根】
二、填空题
(15)求下列各式中x的值
169=100 +27=0
练
【拓展之求平方根】
二、填空题
(16)已知x-2的平方根是±4, 2x-y+12的立方根是4,求x+y的算术平方根
