2021-2022学年北师大版九年级数学上册第四章图形的相似培优试题二(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第四章图形的相似培优试题二(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 23:12:11 | ||
图片预览




文档简介
2021北师大版九上数学第四章图形的相似培优试题二
一、单选题
1.(2021八下·岱岳期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2∶1,把△EFO缩小,则点E的对应点E′的坐标是( )
A. (﹣2,1) B. (﹣8,4) C. (﹣8,4)或(8,﹣4) D. (﹣2,1)或(2,﹣1)
2.(2021八下·泰山期末)如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )
A. 3 B. 3或 C. 3或 D.
3.(2021·玉林模拟)如图,在菱形 中, ,点E,F分别在 , 上,沿 折叠菱形,使点A落在 边上的点G处,且 于点M,若 (取 , ),则 等于( )
A. B. C. D.
4.(2021·安徽模拟)如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )
A. 1:2 B. 1:3 C. 2:3 D. 3:4
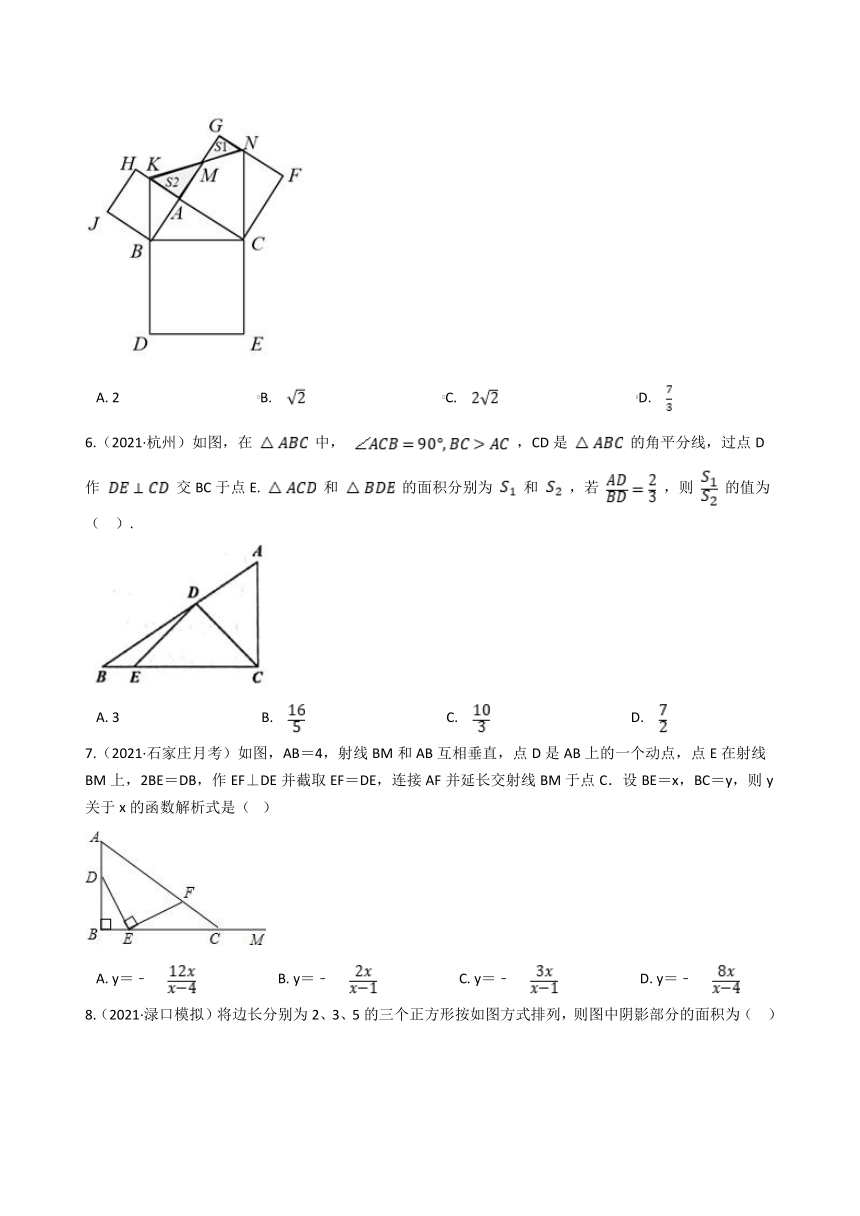
5.(2021·海曙模拟)如图,在Rt△ABC中,∠BAC=90° , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连结KN交AG于点M,若S1-S2=2,AC=4,则AB的长为 ( )
A. 2 B. C. D.
6.(2021·杭州)如图,在 中, ,CD是 的角平分线,过点D作 交BC于点E. 和 的面积分别为 和 ,若 ,则 的值为( ).
A. 3 B. C. D.
7.(2021·石家庄月考)如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )
A. y=﹣ B. y=﹣ C. y=﹣ D. y=﹣
8.(2021·渌口模拟)将边长分别为2、3、5的三个正方形按如图方式排列,则图中阴影部分的面积为( )
A. B. C. D. 3
9.(2021九上·萧山期末)如图, , ,则 ( )
A. B. C. D.
10.(2021九上·犍为期末)如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连 接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )
A. B. C. D. 2
11.(2020九上·江阴期中)如图,点 , , , 在射线 上,点 , , 在射线 上,且 , .若 , 的面积分别为 ,8,则图中三个阴影三角形面积之和为( )
A. B. C. D.
12.(2020八下·渭滨期末)如图,在Rt△ABC中,AC=4,∠ABC=90°,BD是△ABC的角平分线,过点D作DE⊥BD交BC边于点E.若AD=1,则图中阴影部分面积为( )
A. 1 B. 1.5 C. 2 D. 2.5
13.(2020·涪城模拟)如图,在平行四边形ABCD中, , , ,E、F是BC、CD边上点,且 , ,AE 、AF分别交BD于点M , N , 则MN的长度是( )
A. B. C. D.
14.(2020·杭州模拟)如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( )
A. 1 B. 1.2 C. 2 D. 2.5
15.(2020九下·双鸭山期中)如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF= OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF= OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;⑤OG BD=AE2+CF2 . 其中结论正确的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题
16.(2021·汇川模拟)如图, 是等边 边 上的一点,且 ,现将 折叠,使点 与 重合,折痕为 ,点 , 分别在 和 上,则 .
17.(2021·金州模拟)如图,在平行四边形ABCD中,点E在DA的延长线上,且 ,连接CE交BD于点F , 交AB于点G , 则 的值是 .
18.(2021·甘井子模拟)如图,正方形 中, ,点E在边 上,点F在边 上, , 的延长线与射线 相交于点G,设 ,则 的长为 .
19.(2021·越城模拟)如图,在 中, 是 边上的动点,设 .若能在 边上找到一点Q,使 ,则x的取值范围是 .
20.(2021·河南模拟)已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为 .
21.(2021九下·金牛月考)如图,在Rt△ABC中,∠ACB=90°,BC=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP , BP , AP+ =BP的最小值为 .
22.(2020九上·吉水期末)如图示意图,A点的坐标为(2,2),点C在线段OA上运动(点C不与O、A重合),过点C作CD⊥x轴于D,再以CD为一边在CD右侧画正方形CDEF.连接AF并延长交x轴于B,连接OF.若△BEF与△OEF相似,则点B的坐标是 .
23.(2020·武汉模拟)如图,四边形 ABCD 为矩形,点 E 为 BC 上的一点,满足 AB × CF = BE × CE ,连接 DE ,延长 EF交 AD 于 M 点,若 AE2+ FD2 = AF2 , ∠DEF = 15°,则∠M 的度数为________.
24.(2020九下·碑林月考)如图,在△ABC中,∠BAC=90°,AB=3,AC=4,△ADE的顶点D在BC上运动,且∠DAE=90°,∠ADE=∠B,F为线段DE的中点,连接CF,在点D运动过程中,线段CF长的最小值为________.
25.(2019九上·卫辉期中)将三角形纸片( )按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 ,已知 , ,若以点 , , 为顶点的三角形与 相似,那么 的长是________.
26.如图,在矩形 中, , ,点 为 的中点,将 沿 折叠,使点 落在矩形内点 处,连接 ,则 的长为 .
27.如图,已知等边△ABC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D1;过D1作D1E1∥AB于E1 , 连接BE1交AD于D2;过D2作D2E2∥AB于E2 , …,如此继续,若记S△BDE为S1 , 记 为S2 , 记 为S3…,若S△ABC面积为Scm ,则Sn= cm (用含n与S的代数式表示)
28.(2019九上·贵阳期末)在Rt△ABC中,∠BAC=90,AB=AC,AD⊥BC于点D,P是线段AD上的一个动点,以点P为直角的顶点,向上作等腰直角三角形PBE,连接DE,若在点P的运动过程中,DE的最小值为3,则AD的长为________.
三、解答题
29.(2021九上·城阳期中)如图,四边形ABCD中,E为AB的中点,连接CE交DB于点F , BD平分∠ABC , ∠ADB=90°.
求证:
(1)△BFC∽△DFE;
(2)AB=8,BC=3,求 的值.
30.(2021九上·铁东月考)如图,平行四边形ABCD的对角线AC、BD交于点O,点E为边BC上一点,连接AE交BD于点F.
(1)求证:BE AF=BC EF;
(2)若AC⊥AB,AE⊥BC,BE=3,AB=4,求 的值.
31.(2021八下·泰山期末)如图,在 中,点 、 分刷在边 、 上,连接 、 .且 .
(1)证明: ;
(2)若 , ,当点 在 上运动时(点 不与 、 重合).且 是等腰三角形,求此时 的长.
32.(2021·韩城模拟)青龙寺是西安最著名的櫻花观赏地,品种达到了13种之多,每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(櫻花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆 ,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离 米.已知 米, 米, 米,点C、F、H、A在一条直线上,点M在 上, , , , .根据以上测量过程及测量数据,请你求出这棵樱花树 的高度.
33.(2021九下·樊城期中)在矩形 中,点 是对角线 、 的交点,直角 的顶点 与 重合, 、 分别与 、 边相交于 、 ,连接 , ( 为常数).
(1)发现问题:如图1,若 ,猜想: ________;
(2)类比探究:如图2, ,探究线段 , 之间的数量关系,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,若 , , ,求 的长.
34.(2021·东河模拟)某校数学活动小组在一次活动中,对一个数学问题作如下探究:
(1)问题发现:如图1,在等边 中,点P是边 上任意一点(不含端点B和C),连接 ,以 为边作等边 ,连接 .求证: ;
(2)变式探究:如图2,在等腰 中, ,点P是边 上任意一点(不含端点B和C),连接 以 为腰作等腰 ,使 ,连接 .判断 和 的数量关系,并说明理由;
(3)解决问题:如图3,在正方形 中,点P是边 上一点,以 为边作正方形 ,Q是正方形 的中心,连接 .若正方形 的边长为8, ,求正方形 的边长.
35.(2021·岱岳模拟)如图
(1)如图①, ,求证: .
(2)(尝试应用)
如图②,在菱形 中, ,点E , F分别为边 上两点,将菱形 沿 翻折,点A恰好落在对角线 上的点P处,若 ,求 的值.
(3)(拓展提高)
如图③,在矩形 中,点P是 边上一点,连接 ,若 ,求 的长.
36.(2021·亭湖模拟)如图,已知 和 均为等腰三角形, , ,将这两个三角形放置在一起.
(1)问题发现:
如图①,当 时,点B、D、E在同一直线上,连接CE,则线段BD、CE之间的数量关系是________, ________ ;
(2)拓展探究:
如图②,当 时,点B、D、E不在同一直线上,连接CE,求出线段BD、CE之间的数量关系及BD、CE所在直线相交所成的锐角的大小(都用含 的式子表示),并说明理由:
(3)解决问题:
如图③, , , ,连接CE、BD,在 绕点A旋转的过程中,当CE所在的直线垂直于AD时,请你直接写出BD的长.
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】根据位似的性质,缩小后的点在原点的同侧,为(-2,1),然后求在另一侧为(2,-1).
故答案为:D
【分析】根据位似的性质和点的坐标求解即可。
2.【答案】 B
【解析】【解答】 , ,AQ= ,
, ,AQ=3.
故答案为:B.
【分析】分类讨论,结合图形,利用相似三角形的性质求解即可。
3.【答案】 D
【解析】【解答】解:如图,连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,
∵∠A=60°,
∴∠BAO=30°,
∴AO=AB cos30°= ,
∴AC= ,
∵沿EF折叠菱形,使点A落在BC边上的点G处,
∴EG=AE,
∵EG⊥BD,AC⊥BD,
∴EG∥AC,
∴ ,
又∵EG=AE,
∴ ,
解得AE= ,
∴AE的长为 .
故答案为:D.
【分析】连接AC,交BD于点O,由菱形的性质可得AC⊥BD,AC=2AO,求出∠BAO的度数,表示出AO、AC,由折叠的性质可得:EG=AE,然后根据平行线分线段成比例的性质以及EG=AE可表示出AE.
4.【答案】 A
【解析】【解答】 MN是△ABC的中位线
, ,
G是MN的中点
即
又
即:AF:FB .
故答案为:A.
【分析】根据三角形的中位线的性质得到 , 再利用相似三角形的性质和三角形的中位线求出 , 最后整体代入计算即可。
5.【答案】 A
【解析】【解答】解:∵∠ACB+∠CAN=90°,∠FCN+∠CAN=90°,
∴∠ACB=∠FCN,
在△ABC和△FCN中,
,
∴ ≌ ,
∴AB=FN;
∵∠BAC=∠KBC=90°,
∴△BCK∽△ACB,
∴ ,
∴ ;
设五边形ACFNM的面积为S,
∵S1-S2=2,
∴(S1+S)-(S2+S)=2,
设AB=x,BC=y,
由勾股定理可得, ,
∵S1+S2=S正方形ACFG=AC2=16, S2+S= S梯形CFNK= ,S1-S2=2,
∴(S1+S)-(S2+S)=16- =16- =2,
∴ ,
解得, , , , ,
∵x、y都为正数,
∴ ,
即AB=2,BC= .
故答案为:A.
【分析】利用余角的性质可证得∠ACB=∠FCN,利用ASA证明△ABC≌△FCN,利用全等三角形的性质可证得AB=FN;再证明△BCK∽△ACB,利用相似三角形的对应边成比例,可证得;设五边形ACFNM的面积为S,利用已知条件可得到(S1+S)-(S2+S)=2,设AB=x,BC=y,利用勾股定理可得到x,y的方程,利用S1+S2=S正方形ACFG=AC2=16,S1-S2=2,建立关于x,y的方程组,解方程求出符合题意的x,y的值;可得到AB,BC的长.
6.【答案】 C
【解析】【解答】解:过点D作DM⊥BC于点M,DN⊥AC于点N,如图所示:
∵ ,CD是 的角平分线, ,
∴ ,
∴ ,
∵ ,
∴△AND∽△DMB,
∵ ,
∴ ,
∴ ,
设 ,则有 ,
∴ ,
∴ ,
∵ ,
∴ ;
故答案为:C.
【分析】过点D作DM⊥BC于点M,DN⊥AC于点N,根据角平分线的性质、正方形的性质及等腰直角三角形的性质证DM=MC=EM=DN=CN,根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似可得△AND∽△DMB,可得比例式= , 设DM=MC=EM=DN=CN=m,则BM=3m,于是结合比例式可将AN、BM用含m的代数式表示出来,由线段的构成BE=BM-EM、AC=AN+CN可将BE、AC用含m的代数式表示出来,根据S1=AC·DN、S2=BE·DM可求解.
7.【答案】 A
【解析】【解答】作点F作FG⊥BC于G,
∵∠DEB+∠FEG=90°,∠DEB+∠BDE=90°;
∴∠BDE=∠FEG,
在△DBE与△EGF中,
,
∴△DBE≌△EGF(AAS),
∴EG=DB,FG=BE=x,
∴EG=DB=2BE=2x,
∴GC=y﹣3x,
∵FG⊥BC,AB⊥BC,
∴FG∥AB,
∴△FGC∽△ABC,
∴CG:BC=FG:AB,
即 = ,
∴y=﹣ .
故答案为:A.
【分析】作点F作FG⊥BC于G,依据已知条件求得△DBE≌△EGF,得出FG=BE=x,EG=DB=2x,然后证得△FGC∽△ABC,再根据相似三角形的性质即可求解.
8.【答案】 C
【解析】【解答】解:如图
对角线所分得的三个三角形相似,
根据相似的性质可知5:10=x:5,
解得x=2.5,
即阴影梯形的上底就是3﹣2.5=0.5.
再根据相似的性质可知2:5=y:2.5,
解得:y=1,
所以梯形的下底就是3﹣1=2,
所以阴影梯形的高是(2+0.5)×3÷2=3.75= .
故答案为:C.
【分析】由正方形的对边平行得出对角线所分得的三个三角形相似,然后根据相似形的性质,列比例式分别求出两个小直角三角形的竖直边的长度,则可求出梯形的上下底的长度,然后求面积即可.
9.【答案】 D
【解析】【解答】解:过点G作 交BC于F,如图,
, ,
,
, ,
,
,
,
.
故答案为:D.
【分析】过点D作DF∥CA交BE于F , 利用平行线分线段成比例定理得到 , ,结合已知条件把CF、BD和DF均用含CD的代数式表示,则BG和GE的比值可求.
10.【答案】 B
【解析】【解答】解:记AC与PQ的交点为O.
∵∠BAC=90°,AB=3,AC=4,
∴BC= =5.
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∴PQ最短也就是PO最短.
过O作BC的垂线OP′.
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴ ,
∴OP′= ,
∴则PQ的最小值为2OP′= ,
故答案为 .
【分析】记AC与PQ的交点为O,由平行四边形的性质可知O是AC中点,PQ最短也就是PO最短;过O作BC的垂线P′O,则PO最短为P′O;
接下来可证明△P′OC和△ABC相似,进而利用相似三角形的性质即可求出PQ的最小值.
11.【答案】 C
【解析】【解答】解: ,
,
∽
又∵ , 的面积分别为 ,
同理可得:
∴ 与 是等高不等底的三角形
,
又∵ 的面积是 ,
的面积为
同理可得: 的面积
的面积
三个阴影面积之和
故答案为: .
【分析】由平行线的性质可得∠OB2A2=∠OB3A3 , ∠A2B1B2=∠A3B2B3 , 证明△B1B2A2∽
△B2B3A3 , 结合已知条件可得相似比为1:2,同理可得△A2A3B2与△A3A4B3的相似比为1:2,根据三角形的面积公式可得 , 根据△A3B2B3的面积可得△A2B2A3的面积,同理求出△A3B3A4、△A1B1A2的面积,据此求解.
12.【答案】 B
【解析】【解答】解:作DH⊥BC于H,
∵∠ABC=90°,BD是△ABC的角平分线,
∴∠ABD=∠DBC=45°,
∴△DEB是等腰直角三角形,
设DH=BH=EH=a,
∵DH∥AB,
∴△CDH∽△CAB,
∴ ,
∵AD=1,
∴AC=4,
∴ ,
∴AB= ,CE=2a,
∵ ,
∴ ,
∴ =1,
∴ ,
∴图中阴影部分的面积=
=
=
=
故答案为:B.
【分析】作DH⊥BC于H,得到△DEB是等腰直角三角形,设DH=BH=EH=a,证明△CDH∽△CAB,得到 ,求得AB= ,CE=2a,根据 得到 ,利用阴影面积= 求出答案.
13.【答案】 B
【解析】【解答】过点B作BH⊥DA,交DA延长线于点H,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAH= ,
∵AB=4,
∴AH= , ,
∴DH=6+2=8,
∴BD= ,
∵AD∥BC,
∴△BEM∽△DAM,
∴ ,
∴ ,
∴ ,
∵AB∥CD,
∴△DFN∽△BAN,
∴ ,
∴ ,
∴ ,
∴MN=BD-BM-DN= ,
故答案为:B.
【分析】过点B作BH⊥DA,交DA延长线于点H,利用平行四边形的性质求出DH=8,由勾股定理求出BD= ,由△BEM∽△DAM求出 ,
由△DFN∽△BAN求出 ,再根据MN=BD-BM-DN即可求出答案.
14.【答案】 B
【解析】【解答】解:∵AB∥GH,
∴ ,即 ①,
∵GH∥CD,
∴ ,即 ②,
①+②,得 ,
解得GH=1.2.故答案为:B.
【分析】根据平行线分线段成比例,可得 ,即 ①, ,即 ②,利用等式性质将①+②可得 , 从而求出GH的长.
15.【答案】 C
【解析】【解答】① 四边形 是正方形,
, , ,
,
,
,
,
在 和 中,
,
(ASA),
, ,
,故符合题意;
② ,
,故符合题意;
③ ,故符合题意;
④过点 作 ,
,
,
设 ,则 , ,
,
当 时, 最大;
即在旋转过程中,当 与 的面积之和最大时, ,故不符合题意;
⑤ , ,
,
,
,
, ,
,
在 中, ,
,
,故符合题意.
故答案为: .
【分析】①由四边形 是正方形,直角 ,易证得 (ASA),则可证得结论;
②由①易证得 ,则可证得结论;
③ ,故可得结论;
④首先设 ,则 , ,继而表示出 与 的面积之和,然后利用二次函数的最值问题,求得答案;
⑤易证得 ,然后由相似三角形的对应边成比例,证得 ,再利用 与 的关系, 与 的关系,即可证得结论.
二、填空题
16.【答案】 7:8
【解析】【解答】解:设AD=2k,则DB=3k,
∵△ABC为等边三角形,
∴AB=AC=5k,∠A=∠B=∠C=∠EDF=60°,
∴∠EDA+∠FDB=120°,
又∵∠EDA+∠AED=120°,
∴∠FDB=∠AED,
∴△AED∽△BDF,
由折叠得CE=DE,CF=DF,
∴△AED的周长为7k,△BDF的周长为8k,
∴△AED与△BDF的相似比为7:8,
∴CE:CF=DE:DF=7:8.
故答案为:7:8.
【分析】设AD=2k,则DB=3k,由等边三角形的性质可得AB=AC=5k,∠A=∠B=∠C=∠EDF=60°,推出∠FDB=∠AED,证明△AED∽△BDF,由折叠的性质可得CE=DE,CF=DF,然后表示出△AED、△BDF的周长,求出周长比,利用相似三角形的周长比等于相似比可得CE:CF的值.
17.【答案】
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB//CD , AB=CD
∴△AEG∽△DEC ,
∴
∴
设平行四边形ABCD的AB和CD边上的高为h , 则:
故答案为:
【分析】由平行线的性质得出AB//CD,AB=CD,可证△AEG∽△DEC,利用相似三角形的对应边成比例,可得CD=4AG,设平行四边形ABCD的AB和CD边上的高为h,可得 , 据此计算即可.
18.【答案】
【解析】【解答】解:设BF=x , 则CF=4-x ,
∵ABCD为正方形,
∴DA=AB=4,
在Rt△ADE中,DE2=DA2+AE2=42+12=17,
在Rt△EFB中,EF2=EB2+BF2=(4-1)2+x2=9+x2 ,
在Rt△CDF中,DF2=CD2+CF2=42+(4-x)2=x2-8x+32,
在Rt△DEF中,DF2=DE2+EF2 ,
即x2-8x+32=17+9+x2 ,
∴ ,
,
∵∠BFG=∠CFD , ∠DCF=∠GBF=90°,
∴△FBG∽△FCD ,
∴ ,
∴ ;
故答案为:
【分析】设BF=x,则CF=4-x,由正方形的性质得出DA=AB=4,利用勾股定理先分别求出DE2、EF2 , DF2 , 在Rt△DEF中,利用DF2=DE2+EF2 , 建立方程,求出x值即得BF、CF的长,证明△FBG∽△FCD,利用相似三角形对应边成比例即可求出结论.
19.【答案】 0≤x≤1
【解析】【解答】解:过BP中点O,以BP为直径作圆,
连接QO,当QO⊥AC时,QO最短,即BP最短,CP最长,
∵∠OQC=∠ABC=90°,∠C=∠C,
∴△ABC∽△OQC,
∴ ,
∵AB=3,BC=4,
∴AC=5,
∵PC=x,
∴PB=4-x,
∴QO= (4-x),CO= (4-x)+x= x+2,
∴ ,
解得:x=1,
当P与C重合时,CP=0,
∴x的取值范围是:0≤x≤1,
故答案为:0≤x≤1.
【分析】根据已知首先找出CP取最大值时QO⊥AC,进而求出△ABC∽△OQC,再求出x的最小值,进而求出PC的取值范围即可.
20.【答案】 或
【解析】【解答】解:
设AN=PN=x,则CN=5=x
①当∠NPC=90°时,如图1,
∵∠NPC=∠B=90°,∠C=∠C,
∴△NPC∽△ABC,
即
②当∠PNC=90°时,如图2,
∵∠PNC=∠ABC=90°,∠C=∠C
∴△NPC∽△ABC,
即
综上,PN的长为 或 .
故答案为 : 或 .
【分析】首先由勾股定理结合已知条件可得AC的值,设AN=PN=x,则CN=5=x,①当∠NPC=90°时,易证△NPC∽△ABC,然后由相似三角形对应边成比例求解即可;②当∠PNC=90°时,同理可证△NPC∽△ABC,求出PN的值.
21.【答案】
【解析】【解答】解:连接CB,取BC的中点D,连接DP,AD,
∵圆的半径为2
∴CD=1,CP=2
∴
∵∠PCD=∠BCP,
∴△PCD∽△BCP,
∴ ,
∴PD=BP,
∴AP+BP=AP+PD.
要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,
∴AP+BP最小值为AD的长,
在Rt△ACD中,CD=1,AC=6,
∴ ,
AP+BP的最小值为.
故答案为:.
【分析】连接CB,取BC的中点D,连接DP,AD,可证得CD,CP,CP,CB四条线段成比例,再由∠PCD=∠BCP,可证得△PCD∽△BCP,利用相似三角形的对应边成比例可证得PD=BP,可推出AP+BP=AP+PD;要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,最小值就是线段AD的长;然后在Rt△ACD中,利用勾股定理求出AD的长.
22.【答案】 (1,0)(3,0)(6,0)
【解析】【解答】设
∵A(2,2),
∴
∴CD=OD=DE=EF=t ,
∵CF∥OB ,
∴△ACF∽△AOB,
∴
∴
要使△BEF与△OFE相似,
∵
∴只要 或
即:BE=2t或 ,
①当BE=2t时,BO=4t ,
∴
∴t1=0(舍去)或 ,
∴B(6,0).
②当 时,
(ⅰ)当B在E的左侧时,
∴
∴t1=0(舍去)或
∴B(1,0).
(ⅱ)当B在E的右侧时,
∴
∴t1=0(舍去)或
∴B(3,0).
综上,B(1,0)(3,0)(6,0).
故答案为(1,0)(3,0)(6,0).
【分析】先证明△ACF∽△AOB,再求出最后分类讨论计算求解即可。
23.【答案】 60°
【解析】【解答】解:∵四边形 ABCD 为矩形,
∴∠B=∠C=90°,AD∥BC
∴∠EFC+∠FEC=90°
∵AB × CF = BE × CE ,
∴
∴△ABE∽△ECF
∴∠AEB=∠EFC
∴∠AEB+∠FEC=90°
∴∠AEF=180°-(∠AEB+∠FEC)=90°
在Rt△AEF中,AE2+ EF2 = AF2 ,
∵AE2+ FD2= AF2 ,
∴EF=FD
∴∠DEF=∠EDF=15°
∴∠EFC=∠DEF+∠EDF=30°
∴∠FEC=90°-∠EFC=60°
∵AD∥BC
∴∠M=∠FEC=60°
故答案为:60°.
【分析】根据矩形的性质可得∠B=∠C=90°,AD∥BC,然后根据相似三角形的判定定理即可证出△ABE∽△ECF,从而得出∠AEB=∠EFC,然后求出∠AEF,结合勾股定理和已知条件即可证出EF=FD,根据等边对等角可得∠DEF=∠EDF=15°,然后根据三角形外角的性质、平行线的性质即可求出结论.
24.【答案】 2
【解析】【解答】解:连接CE,如图所示:
BC= = =5,
∵∠BAC=∠DAE=90°,∠ADE=∠B,
∴△ABC∽△ADE,
∴ = ,∠ACD=∠AEG,
∵∠AGE=∠DGC,
∴△AGE∽△DGC,
∴ = ,
∵∠AGD=∠EGC,
∴△AGD∽△EGC,
∴∠ADG=∠ECG,
∵Rt△ADE中,∠ADG+∠AEG=90°,
∴∠ECG+∠ACD=90°,即∠DCE=90°,
∵F是DE的中点,
∴CF= DE,
∵△ABC∽△ADE,
∴当AD⊥BC时,AD最短,此时DE最短,
当AD⊥BC时,△ABC的面积= AD BC= AB AC,
∴AD= = = ,
∵ = ,即 = ,
解得:DE=4,
∴CF= ×4=2,
故答案为:2.
【分析】连接CE,如图所示:首先根据勾股定理算出BC的长,再判断出△ABC∽△ADE,得出 = ,判断出△AGE∽△DGC,得出 = ,接着判断出△AGD∽△EGC,得出∠ADG=∠ECG,根据直角三角形斜边上的中线等于斜边的一半可得CF=DE,再根据当AD⊥BC时,AD最短,此时DE最短,根据直角三角形的面积以及相似三角形的性质,求得DE的最小值,即可得出CF的最小值.
25.【答案】 或
【解析】【解答】解:由折叠得: ,
∵ ,
∴△ABC是等腰三角形,
∵以点 , , 为顶点的三角形与 相似,
∴△ 是等腰三角形,
当 时,即
得 ,
∴CF= ;
当 时,
∵ ∽△BCA,
∴ ,即 ,
得CF= = ,
故答案为: 或 .
【分析】分两种情况 时, 时,根据等腰三角形的性质求线段CF的长.
26.【答案】 7.2
【解析】【解答】∵ 为 的中点, ,
∴ ,
在 中, ,
又∵翻折前后三角形全等,
∴ , ,
∴△ 为等腰三角形,
如下图,过 点作 ,交 于点 ,
则 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ 即 .
∴ ,
又∵ 为等腰三角形,
∴ .
【分析】根据中点的定义得出BE=CE=6,然后根据勾股定理算出AE的长,根据翻折的性质得出BE=EF=CE , ∠BEA=∠FEA ,如下图,过 E 点作 EH⊥FC ,交 CF 于点 H ,根据等腰三角形的三线合一得出∠FEH=∠CEH ,根据等角的余角相等得出∠CEH=∠BAE,进而判断出Rt△ABE∽Rt△EHC ,根据相似三角形对应边成比例建立方程即可求出CH的长,从而得出答案。
27.【答案】
【解析】【解答】解:∵D是边BC的中点,过D作DE∥AB,
∴E为AC的中点,BE⊥AC,
设△ABC的高是h,
过E作EM⊥BC于M,
∵BD=DC,DE∥AB,
∴AE=EC,
∵AD⊥BC,EM⊥BC,
∴AD∥EM,
∴DM=MC,
∴EM= AD= h,∴s1= BC AD= s= ,
∵DE∥AB,D1E1∥AB,
∴ = =2= ,∴s2= AE h﹣ AE h= s= ,同理s3= ,s= ,
…
sn= ,故答案为: .
【分析】根据D是边BC的中点,过D作DE∥AB,得到E为AC的中点,BE⊥AC,设△ABC的高是h,根据三角形的面积公式求出s1= BC AD= s= ,根据DE∥AB,D1E1∥AB,得到 = =2= ,求出s2= ,同理s3= ,s= ,进而得出sn= ,即得到答案.
28.【答案】
【解析】【解答】当DE⊥CE时,DE的有最小值.
连接CE.∵△BAC和△EBP是等腰直角三角形,∴∠EBC+∠CBP=∠CBP+∠PBA=45°,BC= BA,BE= BP,∴∠EBC=∠PBA, ,∴△EBC∽△PBA,∴∠ECB=∠PAB.
∵△BAC是等腰直角三角形,AD⊥BC,∴∠PAB=45°,BD=DC=AD,∴∠ECD=45°.
∵∠DEC=90°,∴△DEC是等腰直角三角形,∴DC= DE= ,∴AD= .
故答案为: .
【分析】当DE⊥CE时,DE的有最小值,连接CE.根据两边成比例且夹角相等,可证△EBC∽△PBA,利用相似三角形的对应角相等可得∠ECB=∠PAB.利用等腰直角三角形的性质可得∠PAB=45°,BD=DC=AD,从而可证△DEC是等腰直角三角形,通过解直角三角形可求出AD=DC= DE= .
三、解答题
29.【答案】 (1)解:∵E为AB的中点,∠ADB=90°,
∴ ,
∴∠EDF=∠EBF,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠EDF=∠CBF,
又∵∠EFD=∠CFB,
∴△BFC∽△DFE;
(2)∵△BFC∽△DFE,
∴ ,
∵AB=8,
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)先求出 ∠EDF=∠EBF, 再求出 ∠EDF=∠CBF, 最后证明求解即可;
(2)先求出 , 再求出 , 最后计算求解即可。
30.【答案】 (1)证明:∵四边形ABCD是平行四边形,
∴ ,且 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴BE AF=BC EF.
(2)解:∵AC⊥AB,四边形ABCD是平行四边形,
∴ ,
∵AE⊥BC ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵BE=3,AB=4,
∴在 中, ,
∴ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ , , , ,
∴ ,
在 中, ,
∴ ,
∴ ,
由(1)知, ,
∴ ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)由四边形ABCD是平行四边形,得出 , 求证出 得出 , , 由 , 即可得出结论;
(2)先证出 , 在 中,利用勾股定理得出AE的值,代入求出 , 由四边形ABCD是平行四边形,得出OC的值,在 中, 利用勾股定理得出OD的值,由此得出BD、BC的值,由(1)知, , 得出BF的值,即可得出答案。
31.【答案】 (1)证明: ,
,
,
,
;
(2)解:当 时,
,
,
,
,
点 与 重合,不合题意舍去;
当 时,如图1,
,
,
,
平分 ,
垂直平分 ,
;
当 时,如图2,
, ,
,
,
,
,
,
,
,
.
综上所述,当 是等腰三角形时, 的长为 或 .
【解析】【分析】(1)先求出∠BAD=180°-∠ADB-∠ADE,再求出∠BAD=∠CDE,最后证明求解即可;
(2)分类讨论,结合图形,利用相似三角形的性质计算求解即可。
32.【答案】 解:过点D作 于点P,交 于点N,过点M作 于点Q,交 于点K,
由题意可得: , 米, , 米, 米.
, , ,
,
, ,
, .
, .
(米).
答:这棵樱花树 的高度是8.8米.
【解析】【分析】 过点D作DP⊥AB于点P,交EF于点N,过点M作MQ⊥AB于点Q,交GH于点K,证得△DEN∽△DBP,△GMK∽△BMQ,利用相似三角形的对应边成比例即可求得AB.
33.【答案】 (1)1
(2)解: .
理由:过 作 于 ,作 于 ,
∵ ,
∴四边形 是矩形.
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
在矩形 中, ,
∵ ,
∴ ,
∴ ,
同理 ,
∴ ,
∴ ;
(3)解:∵ ,
∴ ,
由(2), ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
令 ,则 ,
由题意, ,
由勾股定理得, ,
解得: ,
∴ ,
∴ ,
∴ ,
由(2)知, ,
∴在 中, ,
∴ .
【解析】【解答】解:(1)若 ,则 ,即四边形ABCD为正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∵∠EOF=90°,
∴∠EOB=∠FOC,
∴△OEB≌△OFC,
∴OE=OF,
∴
故答案为:1;
【分析】(1)根据题意可知,此时四边形ABCD为正方形,然后证明△OEB≌△OFC即可得到OE=OF,从而得出结论即可;(2)过 作 于 ,作 于 ,利用相似三角形的判定与性质证明即可;(3)根据题意判定 ,从而得到 ,令 ,则 ,可在Rt△ABC中求出未知数,从而得到BC的长度,最终求得OF和OE的长度,再在Rt△OEF中利用勾股定理求解EF即可.
34.【答案】 (1)证明:∵△ABC与△APQ都是等边三角形,
∴AB=AC,AP=AQ,∠BAC=∠PAQ=60°,
∴∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
,
∴△BAP≌△CAQ(SAS),
∴BP=CQ;
(2)解:∠ABC和∠ACQ的数量关系为:∠ABC=∠ACQ;理由如下:
∵在等腰△ABC中,AB=BC,
∴∠BAC= (180°-∠ABC),
∵在等腰△APQ中,AP=PQ,
∴∠PAQ═ (180°-∠APQ),
∵∠APQ=∠ABC,
∴∠BAC=∠PAQ,
∴△BAC∽△PAQ,
∴ ,
∵∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
∴△BAP∽△CAQ,
∴∠ABC=∠ACQ;
(3)解:连接AB、AQ,如图3所示:
∵四边形ADBC是正方形,
∴ ,∠BAC=45°,
∵Q是正方形APEF的中心,
∴ ,∠PAQ=45°,
∴∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
∵ ,
∴△ABP∽△ACQ,
∴ ,
∵CQ= ,
∴BP= CQ=6,
设PC=x,则BC=AC=6+x=8,
解得:x=2,
∴
在 , ,
答:正方形 的边长为 .
【解析】【分析】(1)先求出 ∠BAP=∠CAQ, 再利用SAS证明证明三角形全等,最后求解即可;
(2)先证明 △BAC∽△PAQ, 再求出 ∠BAP=∠CAQ, 最后求解即可;
(3)先求出 ∠BAP=∠CAQ, 再证明 △ABP∽△ACQ, 最后利用勾股定理求解即可。
35.【答案】 (1)证明:∵ ,
∴ ,即 ,
∵ ,
∴
(2)解:∵四边形 是菱形,
∴ ,
∴ ,
∴ 是等边三角形,
∴ ,
由(1)得, ,
∴ ,
设 ,则
∴ ,
可得 ①, ②,
①-②,得 ,
∴ ,
∴ 的值为
(3)解:如图,在 边上取点E,F,使得 ,设AB=CD=m,
∵四边形 是矩形,
∴ ,
∴ ,
= DF,
,
由(1)可得, ,
∴ ,
∴ ,整理,得 ,
解得 或 (舍去),
∴
【解析】【分析】(1)先求出 , 再根据 证明三角形相似即可;
(2)先求出 是等边三角形, 再求出 , 最后计算求解即可;
(3)先求出 ,再利用锐角三角函数和相似三角形的性质计算求解即可。
36.【答案】 (1);60
(2)解:如图②中, , 、 所在直线相交所成的锐角的大小为 .
理由:延长 交 的延长线于 ,设 交 于点 .
在等腰三角形 中, , ,
,
同理, ,
, ,
,
,
,
, ,
,
.
、 所在直线相交所成的锐角的大小为 .
(3)解:由(2)知, ,
,
在 中, ,
,
①当点 在点 上方时,如图③,
过点 作 交 的延长线于 ,
当 时,可证 ,
,
,
,
四边形 是矩形,
,
矩形 是正方形,
,
在 中,根据勾股定理得, ,
.
②当点 在点 下方时,如图④
同①的方法得, , ,
,
综上所述, 的长为 或 .
【解析】【解答】解:(1)如图①中,
在 为等腰三角形, , ,
是等边三角形,
, ,
同理: , ,
,
,
,
, ,
点 、 、 在同一直线上,
,
,
,
故答案为: ,60.
【分析】(1)易得△ABC、△ADE是等边三角形,由等边三角形的性质可证△ACE≌△ABD,得到CE=BD,∠AEC=∠ADB,根据邻补角的性质可得∠ADB的度数,进而得到∠AEC的度数,最后根据角的和差关系求解即可;
(2)延长BD交CE的延长线于T,设AE交BT于点O,根据三角函数的概念表示出AB、AD,进而证明△ACE∽△ABD,根据相似三角形的性质可表示出BD,接下来根据∠CTO=∠CAB结合三角形内角和定理解答即可;
(3) 由(2)知,△ACE∽△ABD,则BD=CE,然后在Rt△ABC中求出AB的值,①当点E在点D上方时,过点A作AP⊥BD交BD的延长线于P , 易得四边形APDE是正方形,然后在Rt△APB中,应用勾股定理求解;②当点E在点D下方时,同①的方法得:AP=DP=AE= , BP=3 , 进而可得BD的值
一、单选题
1.(2021八下·岱岳期末)在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2∶1,把△EFO缩小,则点E的对应点E′的坐标是( )
A. (﹣2,1) B. (﹣8,4) C. (﹣8,4)或(8,﹣4) D. (﹣2,1)或(2,﹣1)
2.(2021八下·泰山期末)如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )
A. 3 B. 3或 C. 3或 D.
3.(2021·玉林模拟)如图,在菱形 中, ,点E,F分别在 , 上,沿 折叠菱形,使点A落在 边上的点G处,且 于点M,若 (取 , ),则 等于( )
A. B. C. D.
4.(2021·安徽模拟)如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )
A. 1:2 B. 1:3 C. 2:3 D. 3:4
5.(2021·海曙模拟)如图,在Rt△ABC中,∠BAC=90° , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连结KN交AG于点M,若S1-S2=2,AC=4,则AB的长为 ( )
A. 2 B. C. D.
6.(2021·杭州)如图,在 中, ,CD是 的角平分线,过点D作 交BC于点E. 和 的面积分别为 和 ,若 ,则 的值为( ).
A. 3 B. C. D.
7.(2021·石家庄月考)如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,2BE=DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )
A. y=﹣ B. y=﹣ C. y=﹣ D. y=﹣
8.(2021·渌口模拟)将边长分别为2、3、5的三个正方形按如图方式排列,则图中阴影部分的面积为( )
A. B. C. D. 3
9.(2021九上·萧山期末)如图, , ,则 ( )
A. B. C. D.
10.(2021九上·犍为期末)如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连 接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )
A. B. C. D. 2
11.(2020九上·江阴期中)如图,点 , , , 在射线 上,点 , , 在射线 上,且 , .若 , 的面积分别为 ,8,则图中三个阴影三角形面积之和为( )
A. B. C. D.
12.(2020八下·渭滨期末)如图,在Rt△ABC中,AC=4,∠ABC=90°,BD是△ABC的角平分线,过点D作DE⊥BD交BC边于点E.若AD=1,则图中阴影部分面积为( )
A. 1 B. 1.5 C. 2 D. 2.5
13.(2020·涪城模拟)如图,在平行四边形ABCD中, , , ,E、F是BC、CD边上点,且 , ,AE 、AF分别交BD于点M , N , 则MN的长度是( )
A. B. C. D.
14.(2020·杭州模拟)如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( )
A. 1 B. 1.2 C. 2 D. 2.5
15.(2020九下·双鸭山期中)如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF= OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF= OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;⑤OG BD=AE2+CF2 . 其中结论正确的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题
16.(2021·汇川模拟)如图, 是等边 边 上的一点,且 ,现将 折叠,使点 与 重合,折痕为 ,点 , 分别在 和 上,则 .
17.(2021·金州模拟)如图,在平行四边形ABCD中,点E在DA的延长线上,且 ,连接CE交BD于点F , 交AB于点G , 则 的值是 .
18.(2021·甘井子模拟)如图,正方形 中, ,点E在边 上,点F在边 上, , 的延长线与射线 相交于点G,设 ,则 的长为 .
19.(2021·越城模拟)如图,在 中, 是 边上的动点,设 .若能在 边上找到一点Q,使 ,则x的取值范围是 .
20.(2021·河南模拟)已知:Rt△ABC中,∠B=90°,AB=4,BC=3,点M、N分别在边AB、AC上,将△AMN沿直线MN折叠,点A落在点P处,且点P在射线CB上,当△PNC为直角三角形时,PN的长为 .
21.(2021九下·金牛月考)如图,在Rt△ABC中,∠ACB=90°,BC=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP , BP , AP+ =BP的最小值为 .
22.(2020九上·吉水期末)如图示意图,A点的坐标为(2,2),点C在线段OA上运动(点C不与O、A重合),过点C作CD⊥x轴于D,再以CD为一边在CD右侧画正方形CDEF.连接AF并延长交x轴于B,连接OF.若△BEF与△OEF相似,则点B的坐标是 .
23.(2020·武汉模拟)如图,四边形 ABCD 为矩形,点 E 为 BC 上的一点,满足 AB × CF = BE × CE ,连接 DE ,延长 EF交 AD 于 M 点,若 AE2+ FD2 = AF2 , ∠DEF = 15°,则∠M 的度数为________.
24.(2020九下·碑林月考)如图,在△ABC中,∠BAC=90°,AB=3,AC=4,△ADE的顶点D在BC上运动,且∠DAE=90°,∠ADE=∠B,F为线段DE的中点,连接CF,在点D运动过程中,线段CF长的最小值为________.
25.(2019九上·卫辉期中)将三角形纸片( )按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 ,已知 , ,若以点 , , 为顶点的三角形与 相似,那么 的长是________.
26.如图,在矩形 中, , ,点 为 的中点,将 沿 折叠,使点 落在矩形内点 处,连接 ,则 的长为 .
27.如图,已知等边△ABC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D1;过D1作D1E1∥AB于E1 , 连接BE1交AD于D2;过D2作D2E2∥AB于E2 , …,如此继续,若记S△BDE为S1 , 记 为S2 , 记 为S3…,若S△ABC面积为Scm ,则Sn= cm (用含n与S的代数式表示)
28.(2019九上·贵阳期末)在Rt△ABC中,∠BAC=90,AB=AC,AD⊥BC于点D,P是线段AD上的一个动点,以点P为直角的顶点,向上作等腰直角三角形PBE,连接DE,若在点P的运动过程中,DE的最小值为3,则AD的长为________.
三、解答题
29.(2021九上·城阳期中)如图,四边形ABCD中,E为AB的中点,连接CE交DB于点F , BD平分∠ABC , ∠ADB=90°.
求证:
(1)△BFC∽△DFE;
(2)AB=8,BC=3,求 的值.
30.(2021九上·铁东月考)如图,平行四边形ABCD的对角线AC、BD交于点O,点E为边BC上一点,连接AE交BD于点F.
(1)求证:BE AF=BC EF;
(2)若AC⊥AB,AE⊥BC,BE=3,AB=4,求 的值.
31.(2021八下·泰山期末)如图,在 中,点 、 分刷在边 、 上,连接 、 .且 .
(1)证明: ;
(2)若 , ,当点 在 上运动时(点 不与 、 重合).且 是等腰三角形,求此时 的长.
32.(2021·韩城模拟)青龙寺是西安最著名的櫻花观赏地,品种达到了13种之多,每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(櫻花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆 ,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离 米.已知 米, 米, 米,点C、F、H、A在一条直线上,点M在 上, , , , .根据以上测量过程及测量数据,请你求出这棵樱花树 的高度.
33.(2021九下·樊城期中)在矩形 中,点 是对角线 、 的交点,直角 的顶点 与 重合, 、 分别与 、 边相交于 、 ,连接 , ( 为常数).
(1)发现问题:如图1,若 ,猜想: ________;
(2)类比探究:如图2, ,探究线段 , 之间的数量关系,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,若 , , ,求 的长.
34.(2021·东河模拟)某校数学活动小组在一次活动中,对一个数学问题作如下探究:
(1)问题发现:如图1,在等边 中,点P是边 上任意一点(不含端点B和C),连接 ,以 为边作等边 ,连接 .求证: ;
(2)变式探究:如图2,在等腰 中, ,点P是边 上任意一点(不含端点B和C),连接 以 为腰作等腰 ,使 ,连接 .判断 和 的数量关系,并说明理由;
(3)解决问题:如图3,在正方形 中,点P是边 上一点,以 为边作正方形 ,Q是正方形 的中心,连接 .若正方形 的边长为8, ,求正方形 的边长.
35.(2021·岱岳模拟)如图
(1)如图①, ,求证: .
(2)(尝试应用)
如图②,在菱形 中, ,点E , F分别为边 上两点,将菱形 沿 翻折,点A恰好落在对角线 上的点P处,若 ,求 的值.
(3)(拓展提高)
如图③,在矩形 中,点P是 边上一点,连接 ,若 ,求 的长.
36.(2021·亭湖模拟)如图,已知 和 均为等腰三角形, , ,将这两个三角形放置在一起.
(1)问题发现:
如图①,当 时,点B、D、E在同一直线上,连接CE,则线段BD、CE之间的数量关系是________, ________ ;
(2)拓展探究:
如图②,当 时,点B、D、E不在同一直线上,连接CE,求出线段BD、CE之间的数量关系及BD、CE所在直线相交所成的锐角的大小(都用含 的式子表示),并说明理由:
(3)解决问题:
如图③, , , ,连接CE、BD,在 绕点A旋转的过程中,当CE所在的直线垂直于AD时,请你直接写出BD的长.
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】根据位似的性质,缩小后的点在原点的同侧,为(-2,1),然后求在另一侧为(2,-1).
故答案为:D
【分析】根据位似的性质和点的坐标求解即可。
2.【答案】 B
【解析】【解答】 , ,AQ= ,
, ,AQ=3.
故答案为:B.
【分析】分类讨论,结合图形,利用相似三角形的性质求解即可。
3.【答案】 D
【解析】【解答】解:如图,连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,
∵∠A=60°,
∴∠BAO=30°,
∴AO=AB cos30°= ,
∴AC= ,
∵沿EF折叠菱形,使点A落在BC边上的点G处,
∴EG=AE,
∵EG⊥BD,AC⊥BD,
∴EG∥AC,
∴ ,
又∵EG=AE,
∴ ,
解得AE= ,
∴AE的长为 .
故答案为:D.
【分析】连接AC,交BD于点O,由菱形的性质可得AC⊥BD,AC=2AO,求出∠BAO的度数,表示出AO、AC,由折叠的性质可得:EG=AE,然后根据平行线分线段成比例的性质以及EG=AE可表示出AE.
4.【答案】 A
【解析】【解答】 MN是△ABC的中位线
, ,
G是MN的中点
即
又
即:AF:FB .
故答案为:A.
【分析】根据三角形的中位线的性质得到 , 再利用相似三角形的性质和三角形的中位线求出 , 最后整体代入计算即可。
5.【答案】 A
【解析】【解答】解:∵∠ACB+∠CAN=90°,∠FCN+∠CAN=90°,
∴∠ACB=∠FCN,
在△ABC和△FCN中,
,
∴ ≌ ,
∴AB=FN;
∵∠BAC=∠KBC=90°,
∴△BCK∽△ACB,
∴ ,
∴ ;
设五边形ACFNM的面积为S,
∵S1-S2=2,
∴(S1+S)-(S2+S)=2,
设AB=x,BC=y,
由勾股定理可得, ,
∵S1+S2=S正方形ACFG=AC2=16, S2+S= S梯形CFNK= ,S1-S2=2,
∴(S1+S)-(S2+S)=16- =16- =2,
∴ ,
解得, , , , ,
∵x、y都为正数,
∴ ,
即AB=2,BC= .
故答案为:A.
【分析】利用余角的性质可证得∠ACB=∠FCN,利用ASA证明△ABC≌△FCN,利用全等三角形的性质可证得AB=FN;再证明△BCK∽△ACB,利用相似三角形的对应边成比例,可证得;设五边形ACFNM的面积为S,利用已知条件可得到(S1+S)-(S2+S)=2,设AB=x,BC=y,利用勾股定理可得到x,y的方程,利用S1+S2=S正方形ACFG=AC2=16,S1-S2=2,建立关于x,y的方程组,解方程求出符合题意的x,y的值;可得到AB,BC的长.
6.【答案】 C
【解析】【解答】解:过点D作DM⊥BC于点M,DN⊥AC于点N,如图所示:
∵ ,CD是 的角平分线, ,
∴ ,
∴ ,
∵ ,
∴△AND∽△DMB,
∵ ,
∴ ,
∴ ,
设 ,则有 ,
∴ ,
∴ ,
∵ ,
∴ ;
故答案为:C.
【分析】过点D作DM⊥BC于点M,DN⊥AC于点N,根据角平分线的性质、正方形的性质及等腰直角三角形的性质证DM=MC=EM=DN=CN,根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似可得△AND∽△DMB,可得比例式= , 设DM=MC=EM=DN=CN=m,则BM=3m,于是结合比例式可将AN、BM用含m的代数式表示出来,由线段的构成BE=BM-EM、AC=AN+CN可将BE、AC用含m的代数式表示出来,根据S1=AC·DN、S2=BE·DM可求解.
7.【答案】 A
【解析】【解答】作点F作FG⊥BC于G,
∵∠DEB+∠FEG=90°,∠DEB+∠BDE=90°;
∴∠BDE=∠FEG,
在△DBE与△EGF中,
,
∴△DBE≌△EGF(AAS),
∴EG=DB,FG=BE=x,
∴EG=DB=2BE=2x,
∴GC=y﹣3x,
∵FG⊥BC,AB⊥BC,
∴FG∥AB,
∴△FGC∽△ABC,
∴CG:BC=FG:AB,
即 = ,
∴y=﹣ .
故答案为:A.
【分析】作点F作FG⊥BC于G,依据已知条件求得△DBE≌△EGF,得出FG=BE=x,EG=DB=2x,然后证得△FGC∽△ABC,再根据相似三角形的性质即可求解.
8.【答案】 C
【解析】【解答】解:如图
对角线所分得的三个三角形相似,
根据相似的性质可知5:10=x:5,
解得x=2.5,
即阴影梯形的上底就是3﹣2.5=0.5.
再根据相似的性质可知2:5=y:2.5,
解得:y=1,
所以梯形的下底就是3﹣1=2,
所以阴影梯形的高是(2+0.5)×3÷2=3.75= .
故答案为:C.
【分析】由正方形的对边平行得出对角线所分得的三个三角形相似,然后根据相似形的性质,列比例式分别求出两个小直角三角形的竖直边的长度,则可求出梯形的上下底的长度,然后求面积即可.
9.【答案】 D
【解析】【解答】解:过点G作 交BC于F,如图,
, ,
,
, ,
,
,
,
.
故答案为:D.
【分析】过点D作DF∥CA交BE于F , 利用平行线分线段成比例定理得到 , ,结合已知条件把CF、BD和DF均用含CD的代数式表示,则BG和GE的比值可求.
10.【答案】 B
【解析】【解答】解:记AC与PQ的交点为O.
∵∠BAC=90°,AB=3,AC=4,
∴BC= =5.
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∴PQ最短也就是PO最短.
过O作BC的垂线OP′.
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴ ,
∴OP′= ,
∴则PQ的最小值为2OP′= ,
故答案为 .
【分析】记AC与PQ的交点为O,由平行四边形的性质可知O是AC中点,PQ最短也就是PO最短;过O作BC的垂线P′O,则PO最短为P′O;
接下来可证明△P′OC和△ABC相似,进而利用相似三角形的性质即可求出PQ的最小值.
11.【答案】 C
【解析】【解答】解: ,
,
∽
又∵ , 的面积分别为 ,
同理可得:
∴ 与 是等高不等底的三角形
,
又∵ 的面积是 ,
的面积为
同理可得: 的面积
的面积
三个阴影面积之和
故答案为: .
【分析】由平行线的性质可得∠OB2A2=∠OB3A3 , ∠A2B1B2=∠A3B2B3 , 证明△B1B2A2∽
△B2B3A3 , 结合已知条件可得相似比为1:2,同理可得△A2A3B2与△A3A4B3的相似比为1:2,根据三角形的面积公式可得 , 根据△A3B2B3的面积可得△A2B2A3的面积,同理求出△A3B3A4、△A1B1A2的面积,据此求解.
12.【答案】 B
【解析】【解答】解:作DH⊥BC于H,
∵∠ABC=90°,BD是△ABC的角平分线,
∴∠ABD=∠DBC=45°,
∴△DEB是等腰直角三角形,
设DH=BH=EH=a,
∵DH∥AB,
∴△CDH∽△CAB,
∴ ,
∵AD=1,
∴AC=4,
∴ ,
∴AB= ,CE=2a,
∵ ,
∴ ,
∴ =1,
∴ ,
∴图中阴影部分的面积=
=
=
=
故答案为:B.
【分析】作DH⊥BC于H,得到△DEB是等腰直角三角形,设DH=BH=EH=a,证明△CDH∽△CAB,得到 ,求得AB= ,CE=2a,根据 得到 ,利用阴影面积= 求出答案.
13.【答案】 B
【解析】【解答】过点B作BH⊥DA,交DA延长线于点H,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAH= ,
∵AB=4,
∴AH= , ,
∴DH=6+2=8,
∴BD= ,
∵AD∥BC,
∴△BEM∽△DAM,
∴ ,
∴ ,
∴ ,
∵AB∥CD,
∴△DFN∽△BAN,
∴ ,
∴ ,
∴ ,
∴MN=BD-BM-DN= ,
故答案为:B.
【分析】过点B作BH⊥DA,交DA延长线于点H,利用平行四边形的性质求出DH=8,由勾股定理求出BD= ,由△BEM∽△DAM求出 ,
由△DFN∽△BAN求出 ,再根据MN=BD-BM-DN即可求出答案.
14.【答案】 B
【解析】【解答】解:∵AB∥GH,
∴ ,即 ①,
∵GH∥CD,
∴ ,即 ②,
①+②,得 ,
解得GH=1.2.故答案为:B.
【分析】根据平行线分线段成比例,可得 ,即 ①, ,即 ②,利用等式性质将①+②可得 , 从而求出GH的长.
15.【答案】 C
【解析】【解答】① 四边形 是正方形,
, , ,
,
,
,
,
在 和 中,
,
(ASA),
, ,
,故符合题意;
② ,
,故符合题意;
③ ,故符合题意;
④过点 作 ,
,
,
设 ,则 , ,
,
当 时, 最大;
即在旋转过程中,当 与 的面积之和最大时, ,故不符合题意;
⑤ , ,
,
,
,
, ,
,
在 中, ,
,
,故符合题意.
故答案为: .
【分析】①由四边形 是正方形,直角 ,易证得 (ASA),则可证得结论;
②由①易证得 ,则可证得结论;
③ ,故可得结论;
④首先设 ,则 , ,继而表示出 与 的面积之和,然后利用二次函数的最值问题,求得答案;
⑤易证得 ,然后由相似三角形的对应边成比例,证得 ,再利用 与 的关系, 与 的关系,即可证得结论.
二、填空题
16.【答案】 7:8
【解析】【解答】解:设AD=2k,则DB=3k,
∵△ABC为等边三角形,
∴AB=AC=5k,∠A=∠B=∠C=∠EDF=60°,
∴∠EDA+∠FDB=120°,
又∵∠EDA+∠AED=120°,
∴∠FDB=∠AED,
∴△AED∽△BDF,
由折叠得CE=DE,CF=DF,
∴△AED的周长为7k,△BDF的周长为8k,
∴△AED与△BDF的相似比为7:8,
∴CE:CF=DE:DF=7:8.
故答案为:7:8.
【分析】设AD=2k,则DB=3k,由等边三角形的性质可得AB=AC=5k,∠A=∠B=∠C=∠EDF=60°,推出∠FDB=∠AED,证明△AED∽△BDF,由折叠的性质可得CE=DE,CF=DF,然后表示出△AED、△BDF的周长,求出周长比,利用相似三角形的周长比等于相似比可得CE:CF的值.
17.【答案】
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB//CD , AB=CD
∴△AEG∽△DEC ,
∴
∴
设平行四边形ABCD的AB和CD边上的高为h , 则:
故答案为:
【分析】由平行线的性质得出AB//CD,AB=CD,可证△AEG∽△DEC,利用相似三角形的对应边成比例,可得CD=4AG,设平行四边形ABCD的AB和CD边上的高为h,可得 , 据此计算即可.
18.【答案】
【解析】【解答】解:设BF=x , 则CF=4-x ,
∵ABCD为正方形,
∴DA=AB=4,
在Rt△ADE中,DE2=DA2+AE2=42+12=17,
在Rt△EFB中,EF2=EB2+BF2=(4-1)2+x2=9+x2 ,
在Rt△CDF中,DF2=CD2+CF2=42+(4-x)2=x2-8x+32,
在Rt△DEF中,DF2=DE2+EF2 ,
即x2-8x+32=17+9+x2 ,
∴ ,
,
∵∠BFG=∠CFD , ∠DCF=∠GBF=90°,
∴△FBG∽△FCD ,
∴ ,
∴ ;
故答案为:
【分析】设BF=x,则CF=4-x,由正方形的性质得出DA=AB=4,利用勾股定理先分别求出DE2、EF2 , DF2 , 在Rt△DEF中,利用DF2=DE2+EF2 , 建立方程,求出x值即得BF、CF的长,证明△FBG∽△FCD,利用相似三角形对应边成比例即可求出结论.
19.【答案】 0≤x≤1
【解析】【解答】解:过BP中点O,以BP为直径作圆,
连接QO,当QO⊥AC时,QO最短,即BP最短,CP最长,
∵∠OQC=∠ABC=90°,∠C=∠C,
∴△ABC∽△OQC,
∴ ,
∵AB=3,BC=4,
∴AC=5,
∵PC=x,
∴PB=4-x,
∴QO= (4-x),CO= (4-x)+x= x+2,
∴ ,
解得:x=1,
当P与C重合时,CP=0,
∴x的取值范围是:0≤x≤1,
故答案为:0≤x≤1.
【分析】根据已知首先找出CP取最大值时QO⊥AC,进而求出△ABC∽△OQC,再求出x的最小值,进而求出PC的取值范围即可.
20.【答案】 或
【解析】【解答】解:
设AN=PN=x,则CN=5=x
①当∠NPC=90°时,如图1,
∵∠NPC=∠B=90°,∠C=∠C,
∴△NPC∽△ABC,
即
②当∠PNC=90°时,如图2,
∵∠PNC=∠ABC=90°,∠C=∠C
∴△NPC∽△ABC,
即
综上,PN的长为 或 .
故答案为 : 或 .
【分析】首先由勾股定理结合已知条件可得AC的值,设AN=PN=x,则CN=5=x,①当∠NPC=90°时,易证△NPC∽△ABC,然后由相似三角形对应边成比例求解即可;②当∠PNC=90°时,同理可证△NPC∽△ABC,求出PN的值.
21.【答案】
【解析】【解答】解:连接CB,取BC的中点D,连接DP,AD,
∵圆的半径为2
∴CD=1,CP=2
∴
∵∠PCD=∠BCP,
∴△PCD∽△BCP,
∴ ,
∴PD=BP,
∴AP+BP=AP+PD.
要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,
∴AP+BP最小值为AD的长,
在Rt△ACD中,CD=1,AC=6,
∴ ,
AP+BP的最小值为.
故答案为:.
【分析】连接CB,取BC的中点D,连接DP,AD,可证得CD,CP,CP,CB四条线段成比例,再由∠PCD=∠BCP,可证得△PCD∽△BCP,利用相似三角形的对应边成比例可证得PD=BP,可推出AP+BP=AP+PD;要使AP+BP最小,只要AP+PD最小,当点A,P,D在同一条直线时,AP+PD最小,最小值就是线段AD的长;然后在Rt△ACD中,利用勾股定理求出AD的长.
22.【答案】 (1,0)(3,0)(6,0)
【解析】【解答】设
∵A(2,2),
∴
∴CD=OD=DE=EF=t ,
∵CF∥OB ,
∴△ACF∽△AOB,
∴
∴
要使△BEF与△OFE相似,
∵
∴只要 或
即:BE=2t或 ,
①当BE=2t时,BO=4t ,
∴
∴t1=0(舍去)或 ,
∴B(6,0).
②当 时,
(ⅰ)当B在E的左侧时,
∴
∴t1=0(舍去)或
∴B(1,0).
(ⅱ)当B在E的右侧时,
∴
∴t1=0(舍去)或
∴B(3,0).
综上,B(1,0)(3,0)(6,0).
故答案为(1,0)(3,0)(6,0).
【分析】先证明△ACF∽△AOB,再求出最后分类讨论计算求解即可。
23.【答案】 60°
【解析】【解答】解:∵四边形 ABCD 为矩形,
∴∠B=∠C=90°,AD∥BC
∴∠EFC+∠FEC=90°
∵AB × CF = BE × CE ,
∴
∴△ABE∽△ECF
∴∠AEB=∠EFC
∴∠AEB+∠FEC=90°
∴∠AEF=180°-(∠AEB+∠FEC)=90°
在Rt△AEF中,AE2+ EF2 = AF2 ,
∵AE2+ FD2= AF2 ,
∴EF=FD
∴∠DEF=∠EDF=15°
∴∠EFC=∠DEF+∠EDF=30°
∴∠FEC=90°-∠EFC=60°
∵AD∥BC
∴∠M=∠FEC=60°
故答案为:60°.
【分析】根据矩形的性质可得∠B=∠C=90°,AD∥BC,然后根据相似三角形的判定定理即可证出△ABE∽△ECF,从而得出∠AEB=∠EFC,然后求出∠AEF,结合勾股定理和已知条件即可证出EF=FD,根据等边对等角可得∠DEF=∠EDF=15°,然后根据三角形外角的性质、平行线的性质即可求出结论.
24.【答案】 2
【解析】【解答】解:连接CE,如图所示:
BC= = =5,
∵∠BAC=∠DAE=90°,∠ADE=∠B,
∴△ABC∽△ADE,
∴ = ,∠ACD=∠AEG,
∵∠AGE=∠DGC,
∴△AGE∽△DGC,
∴ = ,
∵∠AGD=∠EGC,
∴△AGD∽△EGC,
∴∠ADG=∠ECG,
∵Rt△ADE中,∠ADG+∠AEG=90°,
∴∠ECG+∠ACD=90°,即∠DCE=90°,
∵F是DE的中点,
∴CF= DE,
∵△ABC∽△ADE,
∴当AD⊥BC时,AD最短,此时DE最短,
当AD⊥BC时,△ABC的面积= AD BC= AB AC,
∴AD= = = ,
∵ = ,即 = ,
解得:DE=4,
∴CF= ×4=2,
故答案为:2.
【分析】连接CE,如图所示:首先根据勾股定理算出BC的长,再判断出△ABC∽△ADE,得出 = ,判断出△AGE∽△DGC,得出 = ,接着判断出△AGD∽△EGC,得出∠ADG=∠ECG,根据直角三角形斜边上的中线等于斜边的一半可得CF=DE,再根据当AD⊥BC时,AD最短,此时DE最短,根据直角三角形的面积以及相似三角形的性质,求得DE的最小值,即可得出CF的最小值.
25.【答案】 或
【解析】【解答】解:由折叠得: ,
∵ ,
∴△ABC是等腰三角形,
∵以点 , , 为顶点的三角形与 相似,
∴△ 是等腰三角形,
当 时,即
得 ,
∴CF= ;
当 时,
∵ ∽△BCA,
∴ ,即 ,
得CF= = ,
故答案为: 或 .
【分析】分两种情况 时, 时,根据等腰三角形的性质求线段CF的长.
26.【答案】 7.2
【解析】【解答】∵ 为 的中点, ,
∴ ,
在 中, ,
又∵翻折前后三角形全等,
∴ , ,
∴△ 为等腰三角形,
如下图,过 点作 ,交 于点 ,
则 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ 即 .
∴ ,
又∵ 为等腰三角形,
∴ .
【分析】根据中点的定义得出BE=CE=6,然后根据勾股定理算出AE的长,根据翻折的性质得出BE=EF=CE , ∠BEA=∠FEA ,如下图,过 E 点作 EH⊥FC ,交 CF 于点 H ,根据等腰三角形的三线合一得出∠FEH=∠CEH ,根据等角的余角相等得出∠CEH=∠BAE,进而判断出Rt△ABE∽Rt△EHC ,根据相似三角形对应边成比例建立方程即可求出CH的长,从而得出答案。
27.【答案】
【解析】【解答】解:∵D是边BC的中点,过D作DE∥AB,
∴E为AC的中点,BE⊥AC,
设△ABC的高是h,
过E作EM⊥BC于M,
∵BD=DC,DE∥AB,
∴AE=EC,
∵AD⊥BC,EM⊥BC,
∴AD∥EM,
∴DM=MC,
∴EM= AD= h,∴s1= BC AD= s= ,
∵DE∥AB,D1E1∥AB,
∴ = =2= ,∴s2= AE h﹣ AE h= s= ,同理s3= ,s= ,
…
sn= ,故答案为: .
【分析】根据D是边BC的中点,过D作DE∥AB,得到E为AC的中点,BE⊥AC,设△ABC的高是h,根据三角形的面积公式求出s1= BC AD= s= ,根据DE∥AB,D1E1∥AB,得到 = =2= ,求出s2= ,同理s3= ,s= ,进而得出sn= ,即得到答案.
28.【答案】
【解析】【解答】当DE⊥CE时,DE的有最小值.
连接CE.∵△BAC和△EBP是等腰直角三角形,∴∠EBC+∠CBP=∠CBP+∠PBA=45°,BC= BA,BE= BP,∴∠EBC=∠PBA, ,∴△EBC∽△PBA,∴∠ECB=∠PAB.
∵△BAC是等腰直角三角形,AD⊥BC,∴∠PAB=45°,BD=DC=AD,∴∠ECD=45°.
∵∠DEC=90°,∴△DEC是等腰直角三角形,∴DC= DE= ,∴AD= .
故答案为: .
【分析】当DE⊥CE时,DE的有最小值,连接CE.根据两边成比例且夹角相等,可证△EBC∽△PBA,利用相似三角形的对应角相等可得∠ECB=∠PAB.利用等腰直角三角形的性质可得∠PAB=45°,BD=DC=AD,从而可证△DEC是等腰直角三角形,通过解直角三角形可求出AD=DC= DE= .
三、解答题
29.【答案】 (1)解:∵E为AB的中点,∠ADB=90°,
∴ ,
∴∠EDF=∠EBF,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠EDF=∠CBF,
又∵∠EFD=∠CFB,
∴△BFC∽△DFE;
(2)∵△BFC∽△DFE,
∴ ,
∵AB=8,
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)先求出 ∠EDF=∠EBF, 再求出 ∠EDF=∠CBF, 最后证明求解即可;
(2)先求出 , 再求出 , 最后计算求解即可。
30.【答案】 (1)证明:∵四边形ABCD是平行四边形,
∴ ,且 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴BE AF=BC EF.
(2)解:∵AC⊥AB,四边形ABCD是平行四边形,
∴ ,
∵AE⊥BC ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵BE=3,AB=4,
∴在 中, ,
∴ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ , , , ,
∴ ,
在 中, ,
∴ ,
∴ ,
由(1)知, ,
∴ ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)由四边形ABCD是平行四边形,得出 , 求证出 得出 , , 由 , 即可得出结论;
(2)先证出 , 在 中,利用勾股定理得出AE的值,代入求出 , 由四边形ABCD是平行四边形,得出OC的值,在 中, 利用勾股定理得出OD的值,由此得出BD、BC的值,由(1)知, , 得出BF的值,即可得出答案。
31.【答案】 (1)证明: ,
,
,
,
;
(2)解:当 时,
,
,
,
,
点 与 重合,不合题意舍去;
当 时,如图1,
,
,
,
平分 ,
垂直平分 ,
;
当 时,如图2,
, ,
,
,
,
,
,
,
,
.
综上所述,当 是等腰三角形时, 的长为 或 .
【解析】【分析】(1)先求出∠BAD=180°-∠ADB-∠ADE,再求出∠BAD=∠CDE,最后证明求解即可;
(2)分类讨论,结合图形,利用相似三角形的性质计算求解即可。
32.【答案】 解:过点D作 于点P,交 于点N,过点M作 于点Q,交 于点K,
由题意可得: , 米, , 米, 米.
, , ,
,
, ,
, .
, .
(米).
答:这棵樱花树 的高度是8.8米.
【解析】【分析】 过点D作DP⊥AB于点P,交EF于点N,过点M作MQ⊥AB于点Q,交GH于点K,证得△DEN∽△DBP,△GMK∽△BMQ,利用相似三角形的对应边成比例即可求得AB.
33.【答案】 (1)1
(2)解: .
理由:过 作 于 ,作 于 ,
∵ ,
∴四边形 是矩形.
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
在矩形 中, ,
∵ ,
∴ ,
∴ ,
同理 ,
∴ ,
∴ ;
(3)解:∵ ,
∴ ,
由(2), ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
令 ,则 ,
由题意, ,
由勾股定理得, ,
解得: ,
∴ ,
∴ ,
∴ ,
由(2)知, ,
∴在 中, ,
∴ .
【解析】【解答】解:(1)若 ,则 ,即四边形ABCD为正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∵∠EOF=90°,
∴∠EOB=∠FOC,
∴△OEB≌△OFC,
∴OE=OF,
∴
故答案为:1;
【分析】(1)根据题意可知,此时四边形ABCD为正方形,然后证明△OEB≌△OFC即可得到OE=OF,从而得出结论即可;(2)过 作 于 ,作 于 ,利用相似三角形的判定与性质证明即可;(3)根据题意判定 ,从而得到 ,令 ,则 ,可在Rt△ABC中求出未知数,从而得到BC的长度,最终求得OF和OE的长度,再在Rt△OEF中利用勾股定理求解EF即可.
34.【答案】 (1)证明:∵△ABC与△APQ都是等边三角形,
∴AB=AC,AP=AQ,∠BAC=∠PAQ=60°,
∴∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
,
∴△BAP≌△CAQ(SAS),
∴BP=CQ;
(2)解:∠ABC和∠ACQ的数量关系为:∠ABC=∠ACQ;理由如下:
∵在等腰△ABC中,AB=BC,
∴∠BAC= (180°-∠ABC),
∵在等腰△APQ中,AP=PQ,
∴∠PAQ═ (180°-∠APQ),
∵∠APQ=∠ABC,
∴∠BAC=∠PAQ,
∴△BAC∽△PAQ,
∴ ,
∵∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
∴△BAP∽△CAQ,
∴∠ABC=∠ACQ;
(3)解:连接AB、AQ,如图3所示:
∵四边形ADBC是正方形,
∴ ,∠BAC=45°,
∵Q是正方形APEF的中心,
∴ ,∠PAQ=45°,
∴∠BAP+∠PAC=∠PAC+∠CAQ,
∴∠BAP=∠CAQ,
∵ ,
∴△ABP∽△ACQ,
∴ ,
∵CQ= ,
∴BP= CQ=6,
设PC=x,则BC=AC=6+x=8,
解得:x=2,
∴
在 , ,
答:正方形 的边长为 .
【解析】【分析】(1)先求出 ∠BAP=∠CAQ, 再利用SAS证明证明三角形全等,最后求解即可;
(2)先证明 △BAC∽△PAQ, 再求出 ∠BAP=∠CAQ, 最后求解即可;
(3)先求出 ∠BAP=∠CAQ, 再证明 △ABP∽△ACQ, 最后利用勾股定理求解即可。
35.【答案】 (1)证明:∵ ,
∴ ,即 ,
∵ ,
∴
(2)解:∵四边形 是菱形,
∴ ,
∴ ,
∴ 是等边三角形,
∴ ,
由(1)得, ,
∴ ,
设 ,则
∴ ,
可得 ①, ②,
①-②,得 ,
∴ ,
∴ 的值为
(3)解:如图,在 边上取点E,F,使得 ,设AB=CD=m,
∵四边形 是矩形,
∴ ,
∴ ,
= DF,
,
由(1)可得, ,
∴ ,
∴ ,整理,得 ,
解得 或 (舍去),
∴
【解析】【分析】(1)先求出 , 再根据 证明三角形相似即可;
(2)先求出 是等边三角形, 再求出 , 最后计算求解即可;
(3)先求出 ,再利用锐角三角函数和相似三角形的性质计算求解即可。
36.【答案】 (1);60
(2)解:如图②中, , 、 所在直线相交所成的锐角的大小为 .
理由:延长 交 的延长线于 ,设 交 于点 .
在等腰三角形 中, , ,
,
同理, ,
, ,
,
,
,
, ,
,
.
、 所在直线相交所成的锐角的大小为 .
(3)解:由(2)知, ,
,
在 中, ,
,
①当点 在点 上方时,如图③,
过点 作 交 的延长线于 ,
当 时,可证 ,
,
,
,
四边形 是矩形,
,
矩形 是正方形,
,
在 中,根据勾股定理得, ,
.
②当点 在点 下方时,如图④
同①的方法得, , ,
,
综上所述, 的长为 或 .
【解析】【解答】解:(1)如图①中,
在 为等腰三角形, , ,
是等边三角形,
, ,
同理: , ,
,
,
,
, ,
点 、 、 在同一直线上,
,
,
,
故答案为: ,60.
【分析】(1)易得△ABC、△ADE是等边三角形,由等边三角形的性质可证△ACE≌△ABD,得到CE=BD,∠AEC=∠ADB,根据邻补角的性质可得∠ADB的度数,进而得到∠AEC的度数,最后根据角的和差关系求解即可;
(2)延长BD交CE的延长线于T,设AE交BT于点O,根据三角函数的概念表示出AB、AD,进而证明△ACE∽△ABD,根据相似三角形的性质可表示出BD,接下来根据∠CTO=∠CAB结合三角形内角和定理解答即可;
(3) 由(2)知,△ACE∽△ABD,则BD=CE,然后在Rt△ABC中求出AB的值,①当点E在点D上方时,过点A作AP⊥BD交BD的延长线于P , 易得四边形APDE是正方形,然后在Rt△APB中,应用勾股定理求解;②当点E在点D下方时,同①的方法得:AP=DP=AE= , BP=3 , 进而可得BD的值
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
