苏科版七年级数学上册第6章 平面图形的认识(一)单元综合练习题(word版含解析)
文档属性
| 名称 | 苏科版七年级数学上册第6章 平面图形的认识(一)单元综合练习题(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 09:23:32 | ||
图片预览


文档简介
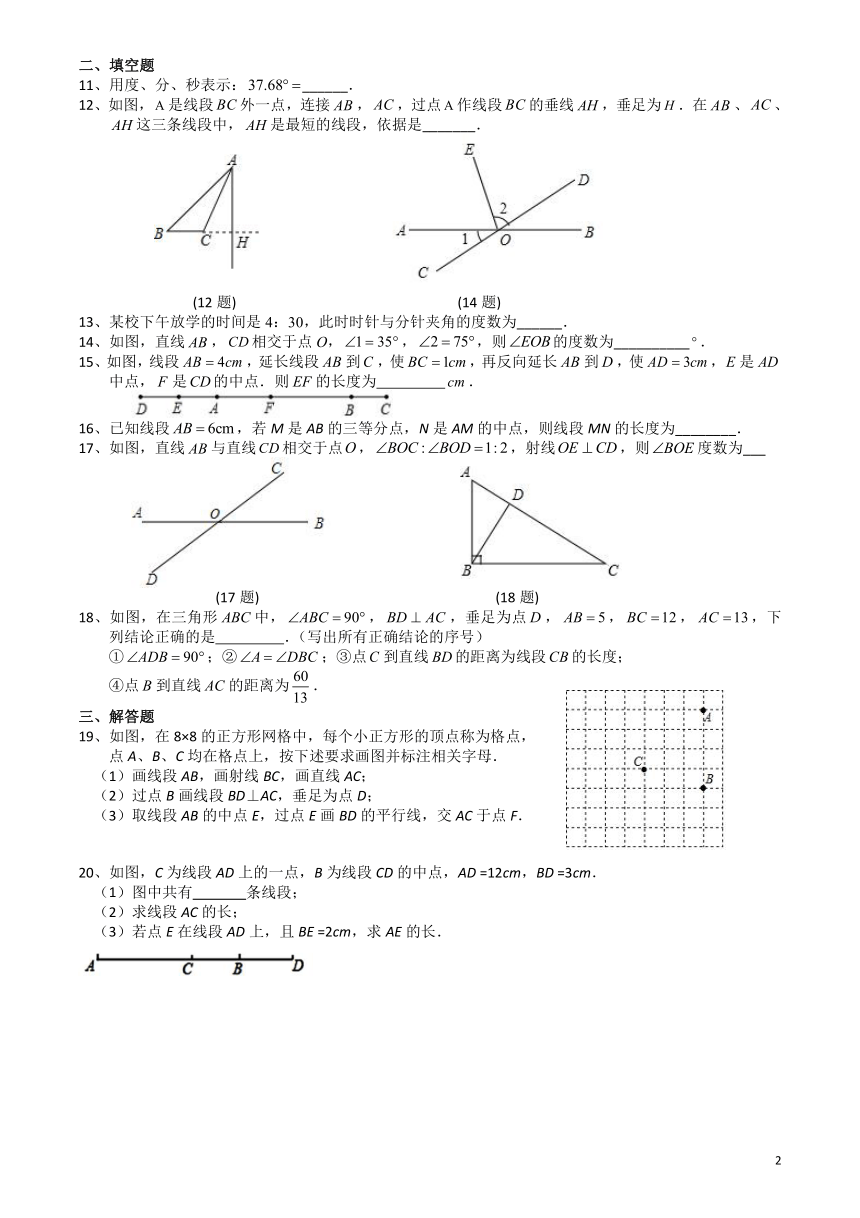
第6章 平面图形的认识(一) 单元综合练习题
2021-2022学年苏科版七年级数学上册
一、选择题
1、如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.连接两点的线段叫做两点的距离
2、如图所示,能用∠α,∠AOB,∠O表示同一个角的是( )
A. B. C. D.
3、下图中,和是对顶角的是( )
A.B. C. D.
4、下列图形中线段AD的长表示点A到直线BC距离的是( )
A. B.C. D.
5、一个角的补角比这个角的余角大( ).
A.70° B.80° C.90° D.100°
6、已知α,β是两个钝角,有四位同学计算(α+β)得出四种不同的答案分别是24°,48°,76°,86°,其中只有一个是正确的,则正确的答案是( )
A.86° B.76° C.48° D.24°
7、如图,线段,点在线段上,为的中点,且,则的长度
A. B. C. D.
8、如图,是的中点,是的中点,则下列等式中正确的是
①;②;③;④.
A.①② B.③④ C.①④ D.②③
9、如图,直线AB,CD相交于点O,OE⊥AB于O,OF平分∠DOE,若∠AOC=32°,则∠AOF的度数为( )
A.119° B.121° C.122° D.124°
10、下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线. ②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
③一条射线把一个角分成两个角,这条射线叫这个角的平分线.
④连结两点的线段叫做两点之间的距离.⑤40°50ˊ=40.5°.⑥互余且相等的两个角都是45°.
A.1个 B.2个 C.3个 D.4个
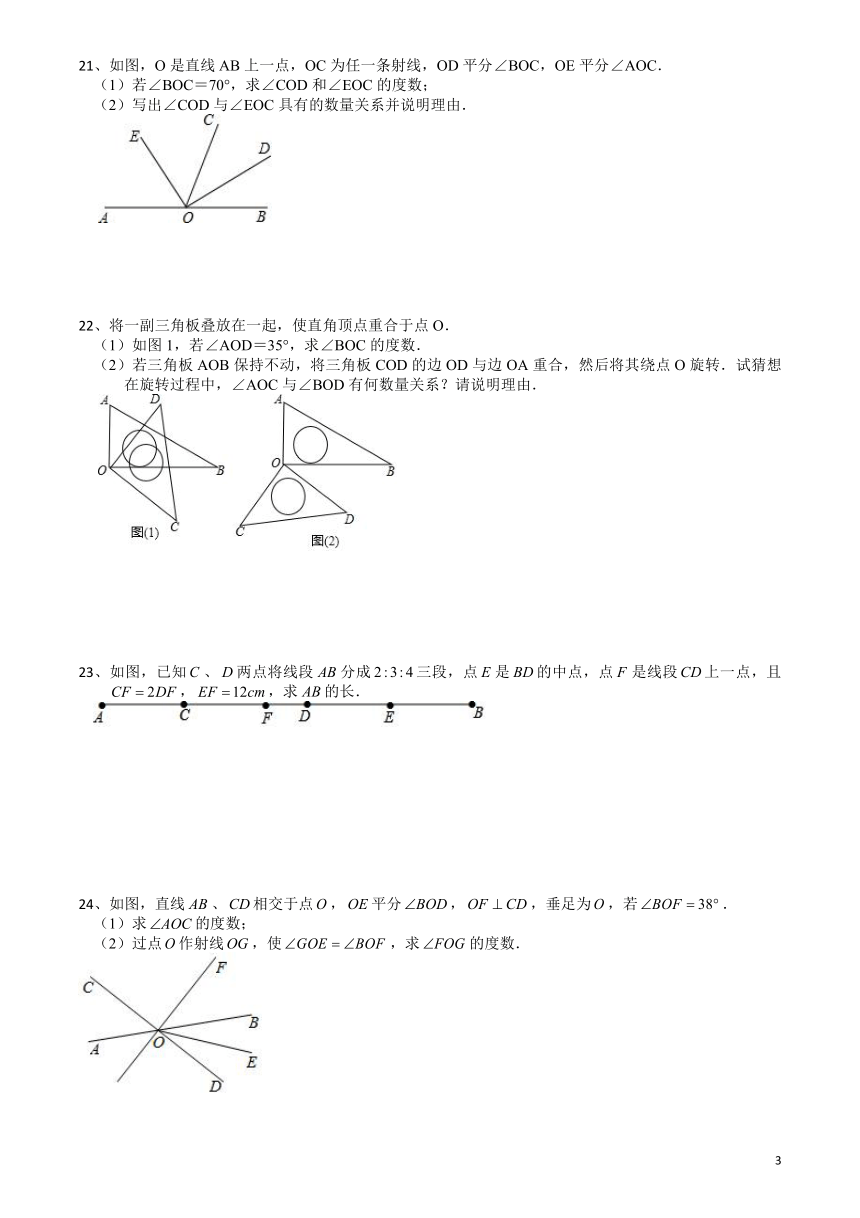
二、填空题
11、用度、分、秒表示:______.
12、如图,是线段外一点,连接,,过点作线段的垂线,垂足为.在、、这三条线段中,是最短的线段,依据是_______.
(12题) (14题)
13、某校下午放学的时间是4:30,此时时针与分针夹角的度数为______.
14、如图,直线,相交于点O,,,则的度数为__________.
15、如图,线段,延长线段到,使,再反向延长到,使,是中点,是的中点.则的长度为 .
16、已知线段,若M是AB的三等分点,N是AM的中点,则线段MN的长度为________.
17、如图,直线与直线相交于点,,射线,则度数为___
(17题) (18题)
18、如图,在三角形中,,,垂足为点,,,,下列结论正确的是 .(写出所有正确结论的序号)
①;②;③点到直线的距离为线段的长度;
④点到直线的距离为.
三、解答题
19、如图,在8×8的正方形网格中,每个小正方形的顶点称为格点,
点A、B、C均在格点上,按下述要求画图并标注相关字母.
(1)画线段AB,画射线BC,画直线AC;
(2)过点B画线段BD⊥AC,垂足为点D;
(3)取线段AB的中点E,过点E画BD的平行线,交AC于点F.
20、如图,C为线段AD上的一点,B为线段CD的中点,AD =12cm,BD =3cm.
(1)图中共有 条线段;
(2)求线段AC的长;
(3)若点E在线段AD上,且BE =2cm,求AE的长.
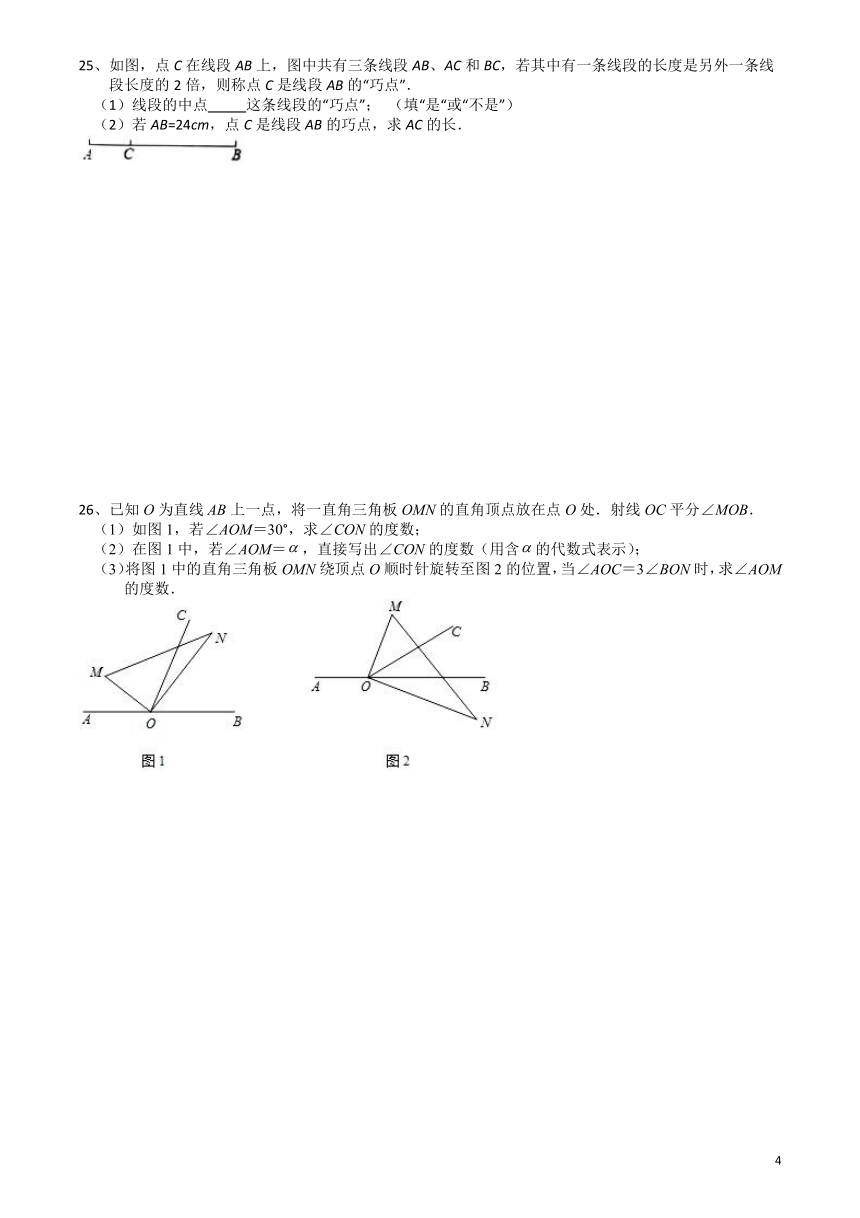
21、如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=70°,求∠COD和∠EOC的度数;
(2)写出∠COD与∠EOC具有的数量关系并说明理由.
22、将一副三角板叠放在一起,使直角顶点重合于点O.
(1)如图1,若∠AOD=35°,求∠BOC的度数.
(2)若三角板AOB保持不动,将三角板COD的边OD与边OA重合,然后将其绕点O旋转.试猜想在旋转过程中,∠AOC与∠BOD有何数量关系?请说明理由.
23、如图,已知、两点将线段分成三段,点是的中点,点是线段上一点,且,,求的长.
24、如图,直线、相交于点,平分,,垂足为,若.
(1)求的度数;
(2)过点作射线,使,求的度数.
25、如图,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”; (填“是“或“不是”)
(2)若AB=24cm,点C是线段AB的巧点,求AC的长.
26、已知O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=,直接写出∠CON的度数(用含的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,当∠AOC=3∠BON时,求∠AOM的度数.
第6章 平面图形的认识(一) 单元综合练习题(解析)
2021-2022学年苏科版七年级数学上册
一、选择题
1、如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.连接两点的线段叫做两点的距离
【答案】A
【分析】根据公理“两点确定一条直线”来解答即可.
【解析】解:经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线.
故选:A.
2、如图所示,能用∠α,∠AOB,∠O表示同一个角的是( )
A. B. C. D.
【分析】
角可以用一个大写字母表示,也可以用三个大写字母表示.角还可以用一个希腊字母表示,或用阿拉伯数字表示.
【详解】
解:能用∠α,∠AOB,∠O三种方法表示同一个角的图形是选项D中的图,选项B,C,D中的图都不能用∠α,∠AOB,∠O三种方法表示同一个角的图形,
故选:D.
3、下图中,和是对顶角的是( )
A.B. C. D.
【答案】C
【分析】
根据对顶角的定义解答即可.
【详解】
解:A. 和的某一边不是互为反向延长线,不是对顶角,故不符合题意;
B. 和没有公共顶点,不是对顶角,故不符合题意;
C. 和是对顶角,符合题意;
D. 和的某一边不是互为反向延长线,不是对顶角,故不符合题意.
故选C.
4、下列图形中线段AD的长表示点A到直线BC距离的是( )
A.B.C. D.
【答案】A
【分析】根据点到直线的距离,垂足在直线上,据此分析即可
【详解】A. 表示的是点A到直线BC距离,故该选项正确,符合题意;
B. 表示的是点到直线距离,故该选项不正确,不符合题意;
C. 表示的是点到直线距离,故该选项不正确,不符合题意;
D. 不能表示点到直线距离,故该选项不正确,不符合题意;故选A
5、一个角的补角比这个角的余角大( ).
A.70° B.80° C.90° D.100°
【答案】C
【分析】
根据互补即两角的和为180°,互余的两角和为90°,设这个角为x,即可求出答案.
【详解】
解:设这个角为x,则这个角的补角为180°-x,这个角的补角为90°-x,
根据题意得:180°-x-(90°-x)=90°,
故选:C.
6、已知α,β是两个钝角,有四位同学计算(α+β)得出四种不同的答案分别是24°,48°,76°,86°,其中只有一个是正确的,则正确的答案是( )
A.86° B.76° C.48° D.24°
【答案】C
【分析】由α,β是两个钝角可得180°<α+β<360°,进一步即可求得(α+β)的范围,从而可得答案.
【详解】解:因为α,β是两个钝角,所以90°<α<180°,90°<β<180°,
所以180°<α+β<360°,所以30°<(α+β)<60°,
在上述四个选项中,只有选项C中48°在上述范围中,故选:C.
7、如图,线段,点在线段上,为的中点,且,则的长度
A. B. C. D.
【分析】设,则,根据线段的中点可得,再根据可得,进而可得答案.
【解析】,
设,则,
为的中点,
,
,解得,
.
故选:.
8、如图,是的中点,是的中点,则下列等式中正确的是
①;②;③;④.
A.①② B.③④ C.①④ D.②③
【分析】根据线段中点的性质,可得,再根据线段的和差,可得答案.
【解析】是的中点,是的中点,
,
,,,,
,故①正确,②不正确;
,③不正确;
,④正确.
正确的有:①④.
故选:.
9、如图,直线AB,CD相交于点O,OE⊥AB于O,OF平分∠DOE,若∠AOC=32°,则∠AOF的度数为( )
A.119° B.121° C.122° D.124°
【答案】A
【分析】根据OE⊥AB于O,即可得出∠BOE=∠AOE=90°,进而求出∠DOE=58°,再利用OF平分∠DOE,即可求出∠EOF的度数,再由∠AOF=∠AOE+∠EOF即可求出∠AOF的度数.
【详解】解:∵OE⊥AB于O,∴∠BOE=∠AOE=90°,
∵∠AOC=32°,∴∠AOC=∠BOD=32°,∴∠DOE=∠BOE﹣∠BOD=90°﹣32°=58°,
∵OF平分∠DOE,∴∠EOFDOE29°,∠AOF=∠AOE+∠EOF=90°+29°=119°.故选:A.
10、下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线. ②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
③一条射线把一个角分成两个角,这条射线叫这个角的平分线.
④连结两点的线段叫做两点之间的距离.⑤40°50ˊ=40.5°.⑥互余且相等的两个角都是45°.
A.1个 B.2个 C.3个 D.4个
【分析】根据射线的定义,同角的补角相等,角平分线的定义,两点之间的距离的定义,度分秒的换算以及余角的定义对各小题分析判断即可得解.
【答案】解:①射线AB与射线BA不表示同一条射线,因为它们的端点不同,故本小题错误;
②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3,正确;
③应为一条射线把一个角分成两个角相等的角,这条射线叫这个角的平分线,故本小题错误;
④应为连结两点的线段的长度叫做两点之间的距离,故本小题错误;
⑤40°50′≈40.83°,故本小题错误;
⑥互余且相等的两个角都是45°,正确.
综上所述,说法正确的有②⑥共2个.
故选:B.
二、填空题
11、用度、分、秒表示:______.
【答案】
【分析】
进行度、分、秒的转化运算,注意以为进制.,.
【详解】
解:
故答案为
12、如图,是线段外一点,连接,,过点作线段的垂线,垂足为.在、、这三条线段中,是最短的线段,依据是_______.
【答案】垂线段最短
【分析】根据垂线段最短的定义求解即可.
【详解】解:∵点到直线的距离,垂线段最短,∴依据是垂线段最短,故答案为:垂线段最短.
13、某校下午放学的时间是4:30,此时时针与分针夹角的度数为______.
【答案】45°
【分析】
根据钟面平均分成12份,可得每份是30°,4点30分时,时针分针相差1.5格,根据时针与分针相距的份数乘以每份的度数,可得答案.
【详解】
解:4:30时,时针与分针的夹角的度数是30°×1.5=45°,
故答案为:45°.
14、如图,直线,相交于点O,,,则的度数为__________.
【答案】110
【分析】
先根据对顶角相等求出∠DOB,进而结合即可求出∠EOB.
【详解】
解:∵∠1=35°,
∴∠DOB=∠1=35°,
又∵∠2=75°,
∴∠EOB=∠2+∠DOB=110°.
故答案为:110.
15、如图,线段,延长线段到,使,再反向延长到,使,是中点,是的中点.则的长度为 .
【分析】结合图形和题意,利用线段的和差知,即可求的长度;再利用中点的定义,求得和的长度,又,即可求得的长度.
【解析】;
是中点,是的中点,
,.
,
故答案为:2.5.
16、已知线段,若M是AB的三等分点,N是AM的中点,则线段MN的长度为________.
【答案】1cm或2cm
【分析】分两种情况考虑点M是AB的三等分点,求出AM的长,由中点定义求出MN即可.
【详解】当M是AB的左三等分点,∵AB=6cm,∴AM=cm,
∵N是AM的中点,∴AN=NM=,
当M是AB的右三等分点,∵AB=6cm,∴AM=cm,
∵N是AM的中点,∴AN=NM=,
线段MN的长度为1cm或2cm.故答案为:1cm或2cm.
17、如图,直线与直线相交于点,,射线,则度数为___
【答案】或
【分析】
根据条件求得∠COB的度数,然后根据∠BOE=∠COE-∠COB即可求解.
【详解】
解:如图,
∵
∴
∵
∴
∴∠BOE=∠COE-∠COB=90°-60°=30°
同理,如图,当点E′在EO的延长线上时,∠BOE′=180°-30°=150°
故答案是:30°或150°.
18、如图,在三角形中,,,垂足为点,,,,下列结论正确的是 .(写出所有正确结论的序号)
①;②;③点到直线的距离为线段的长度;
④点到直线的距离为.
【分析】①根据垂直的定义即可求解;
②根据余角的性质即可求解;
③根据点到直线的距离的定义即可求解;
④根据三角形面积公式即可求解.
【解析】①,
,故①正确;
②,,
,故②正确;
③点到直线的距离为线段的长度,故③错误;
④点到直线的距离为,故④正确.
故答案为:①②④.
三、解答题
19、如图,在8×8的正方形网格中,每个小正方形的顶点称为格点,点A、B、C均在格点上,按下述要求画图并标注相关字母.
(1)画线段AB,画射线BC,画直线AC;
(2)过点B画线段BD⊥AC,垂足为点D;
(3)取线段AB的中点E,过点E画BD的平行线,交AC于点F.
(1)如图所示,线段AB,射线BC,直线AC即为所求;见解析;(2)线段BD即为所求;见解析;(3)直线EF即为所求.见解析.
【解析】(1)连接AB、以B为端点,作射线BC、过点A、C作直线即可;
(2)根据网格结构,作过点B所在的小正方形对角线与直线AC相交于点D,即为所求;
(3)根据网格结构,作过点E所在的小正方形对角线所在的射线与直线AC相交于点F,即为所求.
【详解】
(1)如图所示,线段AB,射线BC,直线AC即为所求;
(2)线段BD即为所求;
(3)直线EF即为所求.
20、如图,C为线段AD上的一点,B为线段CD的中点,AD =12cm,BD =3cm.
(1)图中共有 条线段;
(2)求线段AC的长;
(3)若点E在线段AD上,且BE =2cm,求AE的长.
【答案】(1)6;(2)6cm;(3)11cm或7cm
【分析】(1)根据线段的定义找出线段即可;(2)先根据点B为CD的中点,BD=3cm求出线段CD的长,再根据AC=AD CD即可得出结论;(3)根据E点位置的不同分情况讨论即可求解.
【详解】解:(1)图中的线段有AC、AB、AD、BC、CD、BD,共有6条线段.故答案为:6;
(2)∵点B为CD的中点.∴CD=2BD.∵BD=3cm,∴CD=6cm,BC=3cm,
∵AC=AD CD且AD=12cm,CD=6cm,∴AC=6cm;
(3)如图,点E在B点的左侧,BE =2cm,∴CE=BC-CE=1 cm,∴AE=AC+CE=7 cm,
如图,点E在B点的右侧,BE =2cm,∴AE=AC+BC+BE=6+3+2=11cm,
∴AE的长为11cm或7cm.
21、如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=70°,求∠COD和∠EOC的度数;
(2)写出∠COD与∠EOC具有的数量关系并说明理由.
解:(1)∵OD平分∠BOC,∠BOC=70°,
∴∠COD=∠BOC=×70°=35°,
∵∠BOC=70°,
∴∠AOC=180°﹣∠BOC=180°﹣70°=110°,
∵OE平分∠AOC,
∴∠EOC=∠AOC=×110°=55°;
(2)∠COD与∠EOC互余,
理由如下:∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=∠BOC,∠EOC=∠AOC,
∴∠COD+∠EOC=(∠BOC+∠AOC)=×180°=90°,
∴∠COD与∠EOC互余.
22、将一副三角板叠放在一起,使直角顶点重合于点O.
(1)如图1,若∠AOD=35°,求∠BOC的度数.
(2)若三角板AOB保持不动,将三角板COD的边OD与边OA重合,然后将其绕点O旋转.试猜想在旋转过程中,∠AOC与∠BOD有何数量关系?请说明理由.
【分析】
(1)由于是两直角三角形板重叠,根据∠AOD的度数可得∠BOD,再根据∠DOC=90°可得∠BOC;
(2)当分两种情况:∠AOB与∠DOC有重叠部分时和当∠AOB与∠DOC没有重叠部分时.
【详解】
解:(1)若∠AOD=35°,
∵∠AOB=∠COD=90°,
∴∠BOD=90°﹣35°=55°,
∴∠BOC=90°﹣∠BOD=90°﹣55°=35°;
(2)∠AOC与∠BOD互补.
当∠AOB与∠DOC有重叠部分时,
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
当∠AOB与∠DOC没有重叠部分时,
∠AOB+∠COD+∠AOC+∠BOD=360°,
又∵∠AOC=∠BOD=90°,
∴∠AOB+∠DOC=180°.
23、如图,已知、两点将线段分成三段,点是的中点,点是线段上一点,且,,求的长.
【分析】首先设,则线段,,然后根据是线段的中点,,分别用表示出、,根据,求出的值,即可求出线段的长是多少.
【解析】设,
、两点将线段分成三段,,,
,,,
点是的中点,,
,
,,
,,,
.
24、如图,直线、相交于点,平分,,垂足为,若.
(1)求的度数;
(2)过点作射线,使,求的度数.
【分析】(1)由垂直可得,,由互余得的度数,再由对顶角相等,可得的度数;
(2)射线的位置不确定,需要分类讨论,当射线在射线上方时,当射线在射线下方时,分别求解.
【解析】(1)如图,,垂足为,
,
,
,
.
(2)由(1)知,,
平分,
,
,
,
.
当射线在射线上方时,如图1,
;
当射线在射线下方时,如图2,
.
综上可知,的度数为或.
25、如图,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”; (填“是“或“不是”)
(2)若AB=24cm,点C是线段AB的巧点,求AC的长.
【答案】(1)是;(2)AC=8cm或12cm或16cm.
【分析】(1)根据“巧点”的定义即可求解;
(2)分BC=2AC,AB=2AC,AC=2BC三种情况讨论,分别求解即可.
【详解】解:(1)当M是线段AB的中点,则AB=2AM,
∴线段的中点是这条线段的“巧点”.故答案为:是;
(2)∵AB=24cm,点C是线段AB的巧点,
①BC=2AC,则AC=AB=×24=8(cm);
②AB=2AC,则AC=AB=×24=12(cm);
③AC=2BC,则AC=AB=×24=16(cm).
∴AC=8cm或AC=12cm或AC=16cm.
26、已知O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=,直接写出∠CON的度数(用含的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,当∠AOC=3∠BON时,求∠AOM的度数.
【答案】(1)15°;(2);(3)144°
【分析】
(1)根据补角的定义可得∠BOM=150°,再由∠MON是直角,OC平分∠BOM,即可求解;
(2)根据补角的定义可得∠BOM=180°﹣,再由∠MON是直角,OC平分∠BOM,即可求解;
(3)设∠AOM=x,则∠BOM=180°﹣x,根据OC平分∠BOM,可得∠MOC=90°﹣,从而得到∠AOC=∠AOM+∠MOC=90°+,再由∠MON=90°,可得到∠BON=∠MON﹣∠BOM=x﹣90°,然后根据∠AOC=3∠BON,可得到关于 的方程,即可求解.
【详解】
解:(1)由已知得∠BOM=180°﹣∠AOM=150°,
∵∠MON是直角,OC平分∠BOM,
∴∠CON=∠MON﹣ ∠BOM=90°﹣×150°=15°;
(2)由已知得∠BOM=180°﹣∠AOM=180°﹣,
∵∠MON是直角,OC平分∠BOM,
∴∠CON=∠MON﹣∠BOM=90°﹣×(180°﹣)=;
(3)设∠AOM=x,则∠BOM=180°﹣x,
∵OC平分∠BOM,∴∠MOC=∠BOM=(180°﹣x)=90°﹣,
∴∠AOC=∠AOM+∠MOC=x+90°﹣=90°+,
∵∠MON=90°,∴∠BON=∠MON﹣∠BOM=90°﹣(180°﹣x)=x﹣90°,
∵∠AOC=3∠BON,
∴90°+=3(x﹣90°),解得x=144°,∴∠AOM=144°.
2021-2022学年苏科版七年级数学上册
一、选择题
1、如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.连接两点的线段叫做两点的距离
2、如图所示,能用∠α,∠AOB,∠O表示同一个角的是( )
A. B. C. D.
3、下图中,和是对顶角的是( )
A.B. C. D.
4、下列图形中线段AD的长表示点A到直线BC距离的是( )
A. B.C. D.
5、一个角的补角比这个角的余角大( ).
A.70° B.80° C.90° D.100°
6、已知α,β是两个钝角,有四位同学计算(α+β)得出四种不同的答案分别是24°,48°,76°,86°,其中只有一个是正确的,则正确的答案是( )
A.86° B.76° C.48° D.24°
7、如图,线段,点在线段上,为的中点,且,则的长度
A. B. C. D.
8、如图,是的中点,是的中点,则下列等式中正确的是
①;②;③;④.
A.①② B.③④ C.①④ D.②③
9、如图,直线AB,CD相交于点O,OE⊥AB于O,OF平分∠DOE,若∠AOC=32°,则∠AOF的度数为( )
A.119° B.121° C.122° D.124°
10、下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线. ②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
③一条射线把一个角分成两个角,这条射线叫这个角的平分线.
④连结两点的线段叫做两点之间的距离.⑤40°50ˊ=40.5°.⑥互余且相等的两个角都是45°.
A.1个 B.2个 C.3个 D.4个
二、填空题
11、用度、分、秒表示:______.
12、如图,是线段外一点,连接,,过点作线段的垂线,垂足为.在、、这三条线段中,是最短的线段,依据是_______.
(12题) (14题)
13、某校下午放学的时间是4:30,此时时针与分针夹角的度数为______.
14、如图,直线,相交于点O,,,则的度数为__________.
15、如图,线段,延长线段到,使,再反向延长到,使,是中点,是的中点.则的长度为 .
16、已知线段,若M是AB的三等分点,N是AM的中点,则线段MN的长度为________.
17、如图,直线与直线相交于点,,射线,则度数为___
(17题) (18题)
18、如图,在三角形中,,,垂足为点,,,,下列结论正确的是 .(写出所有正确结论的序号)
①;②;③点到直线的距离为线段的长度;
④点到直线的距离为.
三、解答题
19、如图,在8×8的正方形网格中,每个小正方形的顶点称为格点,
点A、B、C均在格点上,按下述要求画图并标注相关字母.
(1)画线段AB,画射线BC,画直线AC;
(2)过点B画线段BD⊥AC,垂足为点D;
(3)取线段AB的中点E,过点E画BD的平行线,交AC于点F.
20、如图,C为线段AD上的一点,B为线段CD的中点,AD =12cm,BD =3cm.
(1)图中共有 条线段;
(2)求线段AC的长;
(3)若点E在线段AD上,且BE =2cm,求AE的长.
21、如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=70°,求∠COD和∠EOC的度数;
(2)写出∠COD与∠EOC具有的数量关系并说明理由.
22、将一副三角板叠放在一起,使直角顶点重合于点O.
(1)如图1,若∠AOD=35°,求∠BOC的度数.
(2)若三角板AOB保持不动,将三角板COD的边OD与边OA重合,然后将其绕点O旋转.试猜想在旋转过程中,∠AOC与∠BOD有何数量关系?请说明理由.
23、如图,已知、两点将线段分成三段,点是的中点,点是线段上一点,且,,求的长.
24、如图,直线、相交于点,平分,,垂足为,若.
(1)求的度数;
(2)过点作射线,使,求的度数.
25、如图,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”; (填“是“或“不是”)
(2)若AB=24cm,点C是线段AB的巧点,求AC的长.
26、已知O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=,直接写出∠CON的度数(用含的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,当∠AOC=3∠BON时,求∠AOM的度数.
第6章 平面图形的认识(一) 单元综合练习题(解析)
2021-2022学年苏科版七年级数学上册
一、选择题
1、如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.连接两点的线段叫做两点的距离
【答案】A
【分析】根据公理“两点确定一条直线”来解答即可.
【解析】解:经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线.
故选:A.
2、如图所示,能用∠α,∠AOB,∠O表示同一个角的是( )
A. B. C. D.
【分析】
角可以用一个大写字母表示,也可以用三个大写字母表示.角还可以用一个希腊字母表示,或用阿拉伯数字表示.
【详解】
解:能用∠α,∠AOB,∠O三种方法表示同一个角的图形是选项D中的图,选项B,C,D中的图都不能用∠α,∠AOB,∠O三种方法表示同一个角的图形,
故选:D.
3、下图中,和是对顶角的是( )
A.B. C. D.
【答案】C
【分析】
根据对顶角的定义解答即可.
【详解】
解:A. 和的某一边不是互为反向延长线,不是对顶角,故不符合题意;
B. 和没有公共顶点,不是对顶角,故不符合题意;
C. 和是对顶角,符合题意;
D. 和的某一边不是互为反向延长线,不是对顶角,故不符合题意.
故选C.
4、下列图形中线段AD的长表示点A到直线BC距离的是( )
A.B.C. D.
【答案】A
【分析】根据点到直线的距离,垂足在直线上,据此分析即可
【详解】A. 表示的是点A到直线BC距离,故该选项正确,符合题意;
B. 表示的是点到直线距离,故该选项不正确,不符合题意;
C. 表示的是点到直线距离,故该选项不正确,不符合题意;
D. 不能表示点到直线距离,故该选项不正确,不符合题意;故选A
5、一个角的补角比这个角的余角大( ).
A.70° B.80° C.90° D.100°
【答案】C
【分析】
根据互补即两角的和为180°,互余的两角和为90°,设这个角为x,即可求出答案.
【详解】
解:设这个角为x,则这个角的补角为180°-x,这个角的补角为90°-x,
根据题意得:180°-x-(90°-x)=90°,
故选:C.
6、已知α,β是两个钝角,有四位同学计算(α+β)得出四种不同的答案分别是24°,48°,76°,86°,其中只有一个是正确的,则正确的答案是( )
A.86° B.76° C.48° D.24°
【答案】C
【分析】由α,β是两个钝角可得180°<α+β<360°,进一步即可求得(α+β)的范围,从而可得答案.
【详解】解:因为α,β是两个钝角,所以90°<α<180°,90°<β<180°,
所以180°<α+β<360°,所以30°<(α+β)<60°,
在上述四个选项中,只有选项C中48°在上述范围中,故选:C.
7、如图,线段,点在线段上,为的中点,且,则的长度
A. B. C. D.
【分析】设,则,根据线段的中点可得,再根据可得,进而可得答案.
【解析】,
设,则,
为的中点,
,
,解得,
.
故选:.
8、如图,是的中点,是的中点,则下列等式中正确的是
①;②;③;④.
A.①② B.③④ C.①④ D.②③
【分析】根据线段中点的性质,可得,再根据线段的和差,可得答案.
【解析】是的中点,是的中点,
,
,,,,
,故①正确,②不正确;
,③不正确;
,④正确.
正确的有:①④.
故选:.
9、如图,直线AB,CD相交于点O,OE⊥AB于O,OF平分∠DOE,若∠AOC=32°,则∠AOF的度数为( )
A.119° B.121° C.122° D.124°
【答案】A
【分析】根据OE⊥AB于O,即可得出∠BOE=∠AOE=90°,进而求出∠DOE=58°,再利用OF平分∠DOE,即可求出∠EOF的度数,再由∠AOF=∠AOE+∠EOF即可求出∠AOF的度数.
【详解】解:∵OE⊥AB于O,∴∠BOE=∠AOE=90°,
∵∠AOC=32°,∴∠AOC=∠BOD=32°,∴∠DOE=∠BOE﹣∠BOD=90°﹣32°=58°,
∵OF平分∠DOE,∴∠EOFDOE29°,∠AOF=∠AOE+∠EOF=90°+29°=119°.故选:A.
10、下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线. ②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
③一条射线把一个角分成两个角,这条射线叫这个角的平分线.
④连结两点的线段叫做两点之间的距离.⑤40°50ˊ=40.5°.⑥互余且相等的两个角都是45°.
A.1个 B.2个 C.3个 D.4个
【分析】根据射线的定义,同角的补角相等,角平分线的定义,两点之间的距离的定义,度分秒的换算以及余角的定义对各小题分析判断即可得解.
【答案】解:①射线AB与射线BA不表示同一条射线,因为它们的端点不同,故本小题错误;
②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3,正确;
③应为一条射线把一个角分成两个角相等的角,这条射线叫这个角的平分线,故本小题错误;
④应为连结两点的线段的长度叫做两点之间的距离,故本小题错误;
⑤40°50′≈40.83°,故本小题错误;
⑥互余且相等的两个角都是45°,正确.
综上所述,说法正确的有②⑥共2个.
故选:B.
二、填空题
11、用度、分、秒表示:______.
【答案】
【分析】
进行度、分、秒的转化运算,注意以为进制.,.
【详解】
解:
故答案为
12、如图,是线段外一点,连接,,过点作线段的垂线,垂足为.在、、这三条线段中,是最短的线段,依据是_______.
【答案】垂线段最短
【分析】根据垂线段最短的定义求解即可.
【详解】解:∵点到直线的距离,垂线段最短,∴依据是垂线段最短,故答案为:垂线段最短.
13、某校下午放学的时间是4:30,此时时针与分针夹角的度数为______.
【答案】45°
【分析】
根据钟面平均分成12份,可得每份是30°,4点30分时,时针分针相差1.5格,根据时针与分针相距的份数乘以每份的度数,可得答案.
【详解】
解:4:30时,时针与分针的夹角的度数是30°×1.5=45°,
故答案为:45°.
14、如图,直线,相交于点O,,,则的度数为__________.
【答案】110
【分析】
先根据对顶角相等求出∠DOB,进而结合即可求出∠EOB.
【详解】
解:∵∠1=35°,
∴∠DOB=∠1=35°,
又∵∠2=75°,
∴∠EOB=∠2+∠DOB=110°.
故答案为:110.
15、如图,线段,延长线段到,使,再反向延长到,使,是中点,是的中点.则的长度为 .
【分析】结合图形和题意,利用线段的和差知,即可求的长度;再利用中点的定义,求得和的长度,又,即可求得的长度.
【解析】;
是中点,是的中点,
,.
,
故答案为:2.5.
16、已知线段,若M是AB的三等分点,N是AM的中点,则线段MN的长度为________.
【答案】1cm或2cm
【分析】分两种情况考虑点M是AB的三等分点,求出AM的长,由中点定义求出MN即可.
【详解】当M是AB的左三等分点,∵AB=6cm,∴AM=cm,
∵N是AM的中点,∴AN=NM=,
当M是AB的右三等分点,∵AB=6cm,∴AM=cm,
∵N是AM的中点,∴AN=NM=,
线段MN的长度为1cm或2cm.故答案为:1cm或2cm.
17、如图,直线与直线相交于点,,射线,则度数为___
【答案】或
【分析】
根据条件求得∠COB的度数,然后根据∠BOE=∠COE-∠COB即可求解.
【详解】
解:如图,
∵
∴
∵
∴
∴∠BOE=∠COE-∠COB=90°-60°=30°
同理,如图,当点E′在EO的延长线上时,∠BOE′=180°-30°=150°
故答案是:30°或150°.
18、如图,在三角形中,,,垂足为点,,,,下列结论正确的是 .(写出所有正确结论的序号)
①;②;③点到直线的距离为线段的长度;
④点到直线的距离为.
【分析】①根据垂直的定义即可求解;
②根据余角的性质即可求解;
③根据点到直线的距离的定义即可求解;
④根据三角形面积公式即可求解.
【解析】①,
,故①正确;
②,,
,故②正确;
③点到直线的距离为线段的长度,故③错误;
④点到直线的距离为,故④正确.
故答案为:①②④.
三、解答题
19、如图,在8×8的正方形网格中,每个小正方形的顶点称为格点,点A、B、C均在格点上,按下述要求画图并标注相关字母.
(1)画线段AB,画射线BC,画直线AC;
(2)过点B画线段BD⊥AC,垂足为点D;
(3)取线段AB的中点E,过点E画BD的平行线,交AC于点F.
(1)如图所示,线段AB,射线BC,直线AC即为所求;见解析;(2)线段BD即为所求;见解析;(3)直线EF即为所求.见解析.
【解析】(1)连接AB、以B为端点,作射线BC、过点A、C作直线即可;
(2)根据网格结构,作过点B所在的小正方形对角线与直线AC相交于点D,即为所求;
(3)根据网格结构,作过点E所在的小正方形对角线所在的射线与直线AC相交于点F,即为所求.
【详解】
(1)如图所示,线段AB,射线BC,直线AC即为所求;
(2)线段BD即为所求;
(3)直线EF即为所求.
20、如图,C为线段AD上的一点,B为线段CD的中点,AD =12cm,BD =3cm.
(1)图中共有 条线段;
(2)求线段AC的长;
(3)若点E在线段AD上,且BE =2cm,求AE的长.
【答案】(1)6;(2)6cm;(3)11cm或7cm
【分析】(1)根据线段的定义找出线段即可;(2)先根据点B为CD的中点,BD=3cm求出线段CD的长,再根据AC=AD CD即可得出结论;(3)根据E点位置的不同分情况讨论即可求解.
【详解】解:(1)图中的线段有AC、AB、AD、BC、CD、BD,共有6条线段.故答案为:6;
(2)∵点B为CD的中点.∴CD=2BD.∵BD=3cm,∴CD=6cm,BC=3cm,
∵AC=AD CD且AD=12cm,CD=6cm,∴AC=6cm;
(3)如图,点E在B点的左侧,BE =2cm,∴CE=BC-CE=1 cm,∴AE=AC+CE=7 cm,
如图,点E在B点的右侧,BE =2cm,∴AE=AC+BC+BE=6+3+2=11cm,
∴AE的长为11cm或7cm.
21、如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=70°,求∠COD和∠EOC的度数;
(2)写出∠COD与∠EOC具有的数量关系并说明理由.
解:(1)∵OD平分∠BOC,∠BOC=70°,
∴∠COD=∠BOC=×70°=35°,
∵∠BOC=70°,
∴∠AOC=180°﹣∠BOC=180°﹣70°=110°,
∵OE平分∠AOC,
∴∠EOC=∠AOC=×110°=55°;
(2)∠COD与∠EOC互余,
理由如下:∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=∠BOC,∠EOC=∠AOC,
∴∠COD+∠EOC=(∠BOC+∠AOC)=×180°=90°,
∴∠COD与∠EOC互余.
22、将一副三角板叠放在一起,使直角顶点重合于点O.
(1)如图1,若∠AOD=35°,求∠BOC的度数.
(2)若三角板AOB保持不动,将三角板COD的边OD与边OA重合,然后将其绕点O旋转.试猜想在旋转过程中,∠AOC与∠BOD有何数量关系?请说明理由.
【分析】
(1)由于是两直角三角形板重叠,根据∠AOD的度数可得∠BOD,再根据∠DOC=90°可得∠BOC;
(2)当分两种情况:∠AOB与∠DOC有重叠部分时和当∠AOB与∠DOC没有重叠部分时.
【详解】
解:(1)若∠AOD=35°,
∵∠AOB=∠COD=90°,
∴∠BOD=90°﹣35°=55°,
∴∠BOC=90°﹣∠BOD=90°﹣55°=35°;
(2)∠AOC与∠BOD互补.
当∠AOB与∠DOC有重叠部分时,
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
当∠AOB与∠DOC没有重叠部分时,
∠AOB+∠COD+∠AOC+∠BOD=360°,
又∵∠AOC=∠BOD=90°,
∴∠AOB+∠DOC=180°.
23、如图,已知、两点将线段分成三段,点是的中点,点是线段上一点,且,,求的长.
【分析】首先设,则线段,,然后根据是线段的中点,,分别用表示出、,根据,求出的值,即可求出线段的长是多少.
【解析】设,
、两点将线段分成三段,,,
,,,
点是的中点,,
,
,,
,,,
.
24、如图,直线、相交于点,平分,,垂足为,若.
(1)求的度数;
(2)过点作射线,使,求的度数.
【分析】(1)由垂直可得,,由互余得的度数,再由对顶角相等,可得的度数;
(2)射线的位置不确定,需要分类讨论,当射线在射线上方时,当射线在射线下方时,分别求解.
【解析】(1)如图,,垂足为,
,
,
,
.
(2)由(1)知,,
平分,
,
,
,
.
当射线在射线上方时,如图1,
;
当射线在射线下方时,如图2,
.
综上可知,的度数为或.
25、如图,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”; (填“是“或“不是”)
(2)若AB=24cm,点C是线段AB的巧点,求AC的长.
【答案】(1)是;(2)AC=8cm或12cm或16cm.
【分析】(1)根据“巧点”的定义即可求解;
(2)分BC=2AC,AB=2AC,AC=2BC三种情况讨论,分别求解即可.
【详解】解:(1)当M是线段AB的中点,则AB=2AM,
∴线段的中点是这条线段的“巧点”.故答案为:是;
(2)∵AB=24cm,点C是线段AB的巧点,
①BC=2AC,则AC=AB=×24=8(cm);
②AB=2AC,则AC=AB=×24=12(cm);
③AC=2BC,则AC=AB=×24=16(cm).
∴AC=8cm或AC=12cm或AC=16cm.
26、已知O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=,直接写出∠CON的度数(用含的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,当∠AOC=3∠BON时,求∠AOM的度数.
【答案】(1)15°;(2);(3)144°
【分析】
(1)根据补角的定义可得∠BOM=150°,再由∠MON是直角,OC平分∠BOM,即可求解;
(2)根据补角的定义可得∠BOM=180°﹣,再由∠MON是直角,OC平分∠BOM,即可求解;
(3)设∠AOM=x,则∠BOM=180°﹣x,根据OC平分∠BOM,可得∠MOC=90°﹣,从而得到∠AOC=∠AOM+∠MOC=90°+,再由∠MON=90°,可得到∠BON=∠MON﹣∠BOM=x﹣90°,然后根据∠AOC=3∠BON,可得到关于 的方程,即可求解.
【详解】
解:(1)由已知得∠BOM=180°﹣∠AOM=150°,
∵∠MON是直角,OC平分∠BOM,
∴∠CON=∠MON﹣ ∠BOM=90°﹣×150°=15°;
(2)由已知得∠BOM=180°﹣∠AOM=180°﹣,
∵∠MON是直角,OC平分∠BOM,
∴∠CON=∠MON﹣∠BOM=90°﹣×(180°﹣)=;
(3)设∠AOM=x,则∠BOM=180°﹣x,
∵OC平分∠BOM,∴∠MOC=∠BOM=(180°﹣x)=90°﹣,
∴∠AOC=∠AOM+∠MOC=x+90°﹣=90°+,
∵∠MON=90°,∴∠BON=∠MON﹣∠BOM=90°﹣(180°﹣x)=x﹣90°,
∵∠AOC=3∠BON,
∴90°+=3(x﹣90°),解得x=144°,∴∠AOM=144°.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
