2021-2022学年高二上学期数学人教A版(2019)选修二4.3.2等比数列的前n项和 课件(14张)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选修二4.3.2等比数列的前n项和 课件(14张) |  | |
| 格式 | ppt | ||
| 文件大小 | 996.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 08:58:00 | ||
图片预览






文档简介
(共14张PPT)
4.3.2 等比数列的前n项和
知识回顾:
2.通项公式:
3.等比数列的主要性质:
②在等比数列{ }中,若
则 ( )
① 成等比数列
(G,a,b ≠ 0)
1.等比数列的定义:
(常数)
( )
传说在很久以前,古印度舍罕王在宫廷单调的生活中,发现了64格棋(也就是现在的国际象棋)的有趣和奥妙,决定要重赏发明人——他的宰相西萨 班 达依尔,让他随意选择奖品.
宰相要求的赏赐是:在棋盘的第一格内赏他
一粒麦子,第二格内赏他两粒麦子,第三格内
赏他四粒麦子……依此类推,每一格上的麦子
数都是前一格的两倍,国王一听,几粒麦子,
加起来也不过一小袋,他就答应了宰相的要求.
实际上国王能满足宰相的要求吗?
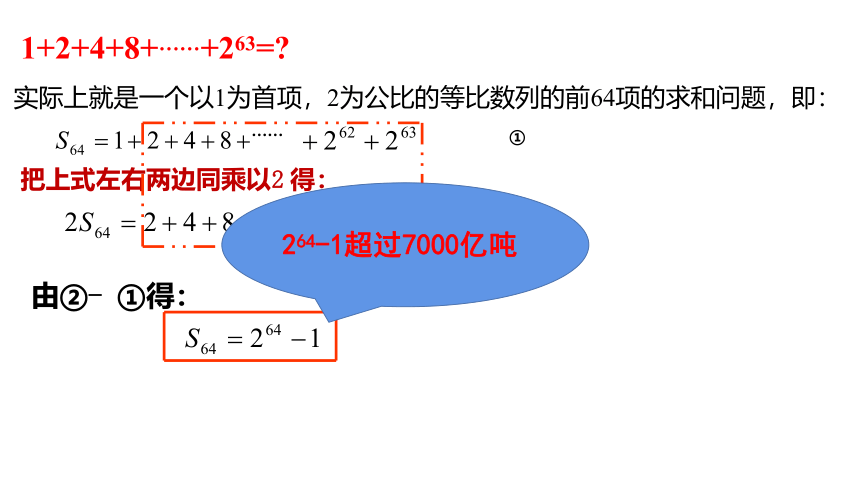
1+2+4+8+……+263=
实际上就是一个以1为首项,2为公比的等比数列的前64项的求和问题,即:
……
①
把上式左右两边同乘以2 得:
……
②
16+
由②- ①得:
1+2+4+8+……+263=
264-1超过7000亿吨
设等比数列
它的前n项和是
错位相减法
探究:已知等比数列{an}的首项为a1,公比为q,如何确定等比数列的前n项和Sn?
1、使用公式求和时,需注意对 q=1 和 q≠1 的情况加以讨论;
注意:
等比数列的前n项和公式
例2:求下列等比数列前n项的和:
1.数列{2n-1}的前99项和为 ( )
A.2100-1 B.1-2100 C.299-1 D.1-299
2.若等比数列{an}的前3项的和为13,首项为1,则其公比为__________.
3.设Sn为等比数列{an}的前n项和,已知3S3=a4-2,3S2=a3-2,则公比q=( )
A.3 B.4 C.5 D.6
解析: 3S3-3S2=3a3=a4-a3 a4=4a3 q=4.
答案: B
【基础测试】
4.3.2 等比数列的前n项和
知识回顾:
2.通项公式:
3.等比数列的主要性质:
②在等比数列{ }中,若
则 ( )
① 成等比数列
(G,a,b ≠ 0)
1.等比数列的定义:
(常数)
( )
传说在很久以前,古印度舍罕王在宫廷单调的生活中,发现了64格棋(也就是现在的国际象棋)的有趣和奥妙,决定要重赏发明人——他的宰相西萨 班 达依尔,让他随意选择奖品.
宰相要求的赏赐是:在棋盘的第一格内赏他
一粒麦子,第二格内赏他两粒麦子,第三格内
赏他四粒麦子……依此类推,每一格上的麦子
数都是前一格的两倍,国王一听,几粒麦子,
加起来也不过一小袋,他就答应了宰相的要求.
实际上国王能满足宰相的要求吗?
1+2+4+8+……+263=
实际上就是一个以1为首项,2为公比的等比数列的前64项的求和问题,即:
……
①
把上式左右两边同乘以2 得:
……
②
16+
由②- ①得:
1+2+4+8+……+263=
264-1超过7000亿吨
设等比数列
它的前n项和是
错位相减法
探究:已知等比数列{an}的首项为a1,公比为q,如何确定等比数列的前n项和Sn?
1、使用公式求和时,需注意对 q=1 和 q≠1 的情况加以讨论;
注意:
等比数列的前n项和公式
例2:求下列等比数列前n项的和:
1.数列{2n-1}的前99项和为 ( )
A.2100-1 B.1-2100 C.299-1 D.1-299
2.若等比数列{an}的前3项的和为13,首项为1,则其公比为__________.
3.设Sn为等比数列{an}的前n项和,已知3S3=a4-2,3S2=a3-2,则公比q=( )
A.3 B.4 C.5 D.6
解析: 3S3-3S2=3a3=a4-a3 a4=4a3 q=4.
答案: B
【基础测试】
