苏科版九年级数学上册第一章一元二次方程单元测试题(Word版含答案)
文档属性
| 名称 | 苏科版九年级数学上册第一章一元二次方程单元测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 44.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
【易错题解析】苏科版九年级数学上册第一章一元二次方程单元测试题
一、单选题(共10题;共30分)
1.一元二次方程x2﹣1=0的根是( )
A. 1 B. ﹣1 C. D. ±1
2.若关于x的一元二次方程x2+(k+3)x+2=0的一个根是﹣1,则另一个根是( )
A. 1 B. 0 C. 2 D. ﹣2
3.关于x的方程2x2+mx+n=0的两个根是﹣2和1,则nm的值为( )
A. ﹣8 B. 8 C. 16 D. ﹣16
4.关于x的一元二次方程的一个根为0,则a的值为( )
A. 1 B. -1 C. 1或-1 D.
5.如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个不相等的实数根,那么k的取值范围是( )
A. k> B. k>且k≠0 C. k< D. k≥且k≠0
6.已知x1、x2是方程x2﹣5x﹣6=0的两个根,则代数式x12+x22的值是( )
A. 37 B. 26 C. 13 D. 10
7.已知方程x2-x+2m=0有两个实数根,则的化简结果是( )
A. m-1 B. m+1 C. 1-m D.
8.已知关于x的方程有且仅有两个不相等的实根,则实数a的取值范围为( )
A. B. C. 或 D. 或
9.若三角形两边长分别为3和4,第三边长是方程x2-12x+35=0的根,该三角形的周长为( )
A. 14 B. 12 C. 12或14 D. 以上都不对
10.为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
A. 289(1﹣x)2=256 B. 256(1﹣x)2=289
C. 289(1﹣2x)=256 D. 256(1﹣2x)=289
二、填空题(共10题;共30分)
11.一元二次方程x2=x的解为________.
12.小华在解一元二次方程时,只得出一个根是x=4,则被他漏掉的一个根是x=________.
13.关于x的一元二次方程x2+a=0没有实数根,则实数a的取值范围是________.
14.设m,nx分别为一元二次方程的两个实数根,则 =________.
15.三角形的两边长为2和4,第三边长是方程x2﹣6x+8=0的根,则这个三角形的周长是________
16.已知一元二次方程(m﹣2)x2﹣3x+m2﹣4=0的一个根为0,则m=________.
17.在实数范围内定义运算“★”,其规则为a★b=a2﹣b2,则方程(4★3)★x=13的根为________.
18.关于x的一元二次方程x2+bx+c=0的两根为x1=﹣1,x2=2,则x2+bx+c可分解为________.
19.如果关于x的方程x2+2(a+1)x+2a+1=0有一个小于1的正数根,那么实数a的取值范围是________.
20.已知α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足,则m的值是________ .
三、解答题(共8题;共60分)
21.解下列方程
(1)2x2-x=0 (2)x2-4x=4
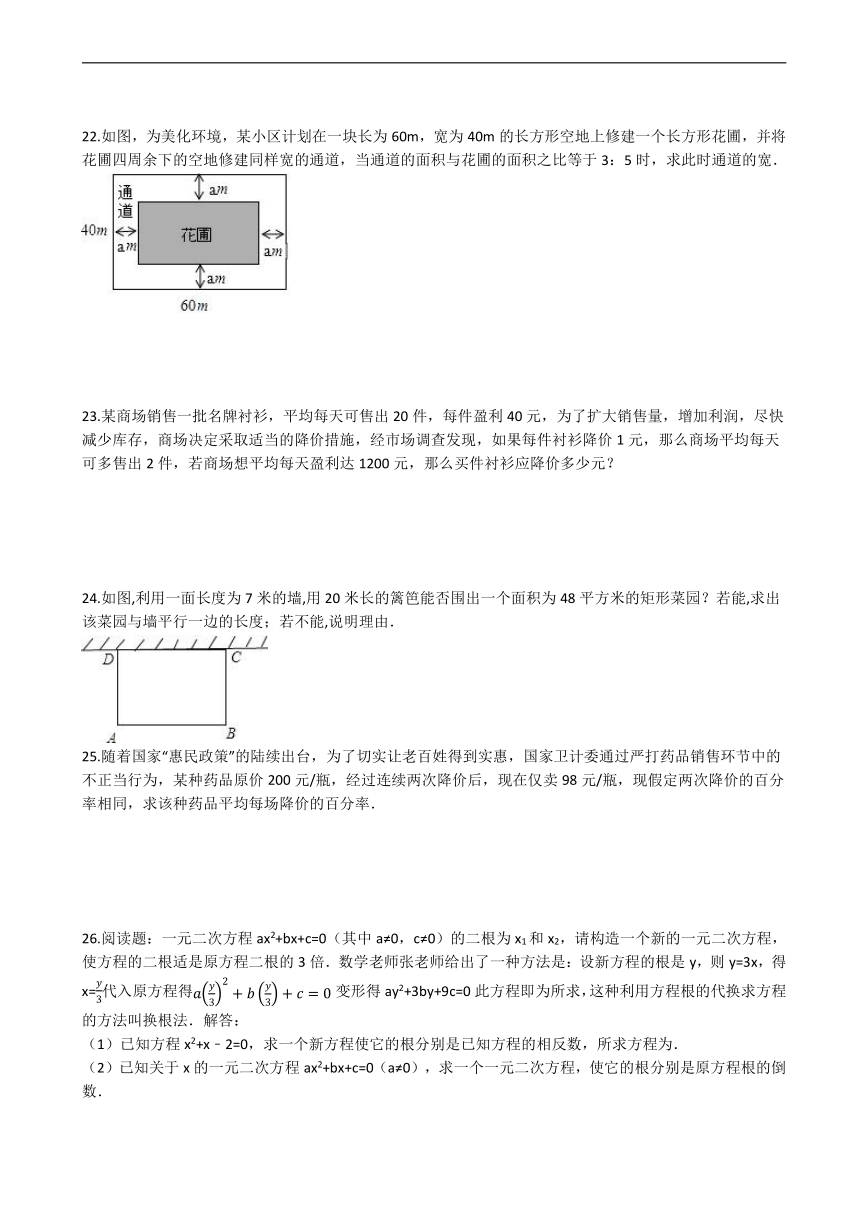
22.如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.
23.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售量,增加利润,尽快减少库存,商场决定采取适当的降价措施,经市场调查发现,如果每件衬衫降价1元,那么商场平均每天可多售出2件,若商场想平均每天盈利达1200元,那么买件衬衫应降价多少元?
24.如图,利用一面长度为7米的墙,用20米长的篱笆能否围出一个面积为48平方米的矩形菜园?若能,求出该菜园与墙平行一边的长度;若不能,说明理由.
25.随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,国家卫计委通过严打药品销售环节中的不正当行为,某种药品原价200元/瓶,经过连续两次降价后,现在仅卖98元/瓶,现假定两次降价的百分率相同,求该种药品平均每场降价的百分率.
26.阅读题:一元二次方程ax2+bx+c=0(其中a≠0,c≠0)的二根为x1和x2,请构造一个新的一元二次方程,使方程的二根适是原方程二根的3倍.数学老师张老师给出了一种方法是:设新方程的根是y,则y=3x,得x=代入原方程得变形得ay2+3by+9c=0此方程即为所求,这种利用方程根的代换求方程的方法叫换根法.解答:
(1)已知方程x2+x﹣2=0,求一个新方程使它的根分别是已知方程的相反数,所求方程为.
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0),求一个一元二次方程,使它的根分别是原方程根的倒数.
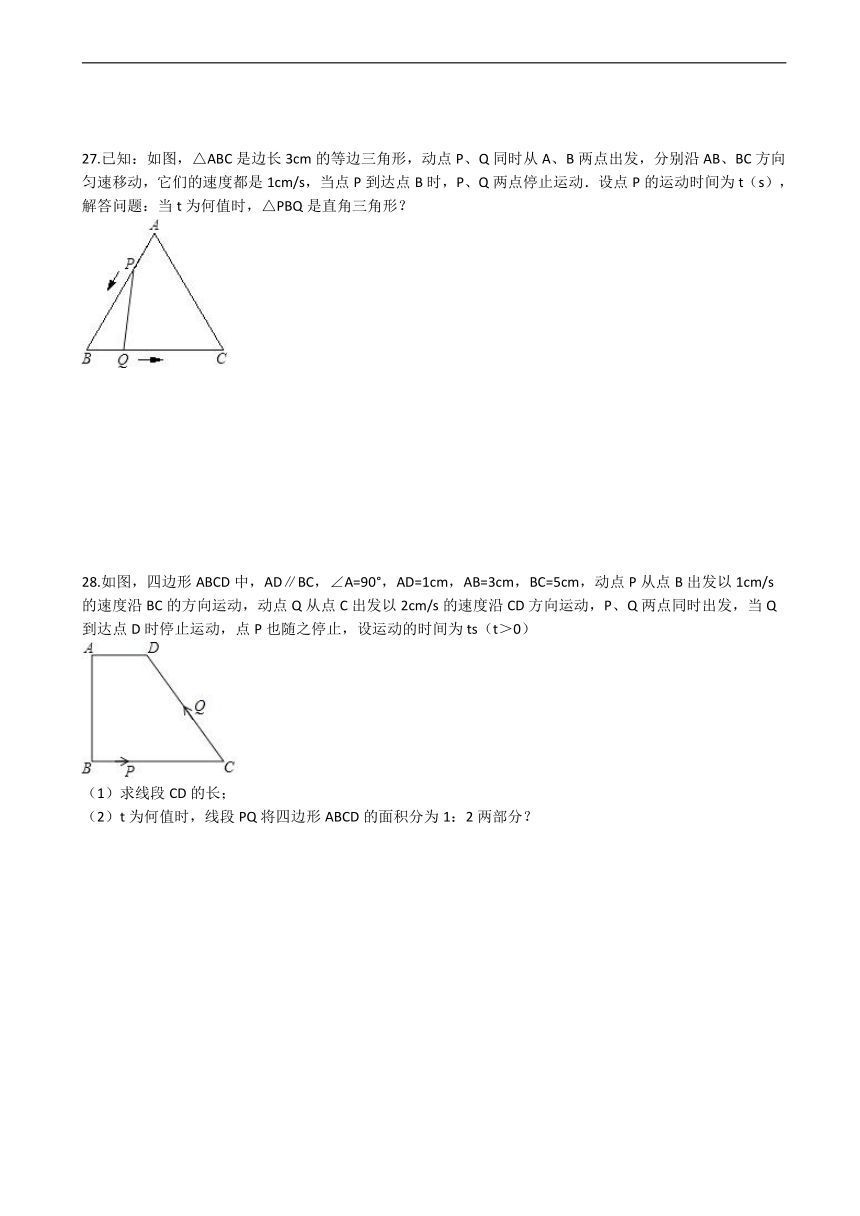
27.已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?
28.如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
答案解析部分
一、单选题
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】A
二、填空题
11.【答案】x1=0,x2=1
12.【答案】0
13.【答案】a>0
14.【答案】2013
15.【答案】10
16.【答案】﹣2
17.【答案】x1=6,x2=﹣6
18.【答案】(x+1)(x﹣2)
19.【答案】-1<a<-
20.【答案】3
三、解答题
21.【答案】(1)解:2x2-x=0,
2x(x-1)=0,
2x=0或x-1=0,
则x1=0,x2=1.
(2)解:方程两边同时+4,得x2-4x+4=4+4,
(x-2)2=8,
x-2=±2 ,
则x1=2+2 ,x2=2-2 .
22.【答案】解:设此时通道的宽为x米,根据题意,得
60×40﹣(60﹣2x)(40﹣2x)= ×60×40,
解得x=5或45,
45不合题意,舍去.
答:此时通道的宽为5米
23.【答案】解:设买件衬衫应降价x元,由题意得:(40﹣x)(20+2x)=1200,
即2x2﹣60x+400=0,
∴x2﹣30x+200=0,
∴(x﹣10)(x﹣20)=0,
解得:x=10或x=20
为了减少库存,所以x=20.
故买件衬衫应应降价20元
24.【答案】
25.【答案】解:设该种药品平均每场降价的百分率是x,由题意得:
解得:(不合题意舍去), =30%.
答:该种药品平均每场降价的百分率是30%.
26.【答案】解:(1)设所求方程的根为y,则y=﹣x,则x=﹣y.
把x=﹣y代入已知方程x2+x﹣2=0,
得(﹣y)2+(﹣y)﹣2=0.
化简得:y2﹣y﹣2=0.
故答案是:y2﹣y﹣2=0.
(2)设所求方程的根为y,则y=,所以x=,
把x=代入已知方程ax2+bx+c=0(a≠0)得
a()2+b +c=0,
去分母,得 a+by+cy2=0.
若c=0,则ax2+bx=0,于是方程ax2+bx+c=0(a≠0)有一根为0,不符合题意.
∴c≠0,
故所求的方程为:cy2+by+c=0(c≠0).
27.【答案】解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=3﹣t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ= BP,
即t= (3﹣t),t=1(秒),
当∠BPQ=90°时,BP= BQ,
3﹣t= t,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形
28.【答案】(1)解:如图1,作DE⊥BC于E,则四边形ADEB是矩形.
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴DC= =5厘米;
(2)解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴ = ,即 = ,
∴QH= t,
∴S△PQC= PC QH= (5﹣t) t=﹣ t2+3t,
S四边形ABCD= (AD+BC) AB= (1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,
﹣ t2+3t= ×9,即t2﹣5t+5=0,
解得t1= ,t2= (舍去);
②S△PQC:S四边形ABCD=2:3时,
﹣ t2+3t= ×9,即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
【易错题解析】苏科版九年级数学上册第一章一元二次方程单元测试题
一、单选题(共10题;共30分)
1.一元二次方程x2﹣1=0的根是( )
A. 1 B. ﹣1 C. D. ±1
2.若关于x的一元二次方程x2+(k+3)x+2=0的一个根是﹣1,则另一个根是( )
A. 1 B. 0 C. 2 D. ﹣2
3.关于x的方程2x2+mx+n=0的两个根是﹣2和1,则nm的值为( )
A. ﹣8 B. 8 C. 16 D. ﹣16
4.关于x的一元二次方程的一个根为0,则a的值为( )
A. 1 B. -1 C. 1或-1 D.
5.如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个不相等的实数根,那么k的取值范围是( )
A. k> B. k>且k≠0 C. k< D. k≥且k≠0
6.已知x1、x2是方程x2﹣5x﹣6=0的两个根,则代数式x12+x22的值是( )
A. 37 B. 26 C. 13 D. 10
7.已知方程x2-x+2m=0有两个实数根,则的化简结果是( )
A. m-1 B. m+1 C. 1-m D.
8.已知关于x的方程有且仅有两个不相等的实根,则实数a的取值范围为( )
A. B. C. 或 D. 或
9.若三角形两边长分别为3和4,第三边长是方程x2-12x+35=0的根,该三角形的周长为( )
A. 14 B. 12 C. 12或14 D. 以上都不对
10.为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
A. 289(1﹣x)2=256 B. 256(1﹣x)2=289
C. 289(1﹣2x)=256 D. 256(1﹣2x)=289
二、填空题(共10题;共30分)
11.一元二次方程x2=x的解为________.
12.小华在解一元二次方程时,只得出一个根是x=4,则被他漏掉的一个根是x=________.
13.关于x的一元二次方程x2+a=0没有实数根,则实数a的取值范围是________.
14.设m,nx分别为一元二次方程的两个实数根,则 =________.
15.三角形的两边长为2和4,第三边长是方程x2﹣6x+8=0的根,则这个三角形的周长是________
16.已知一元二次方程(m﹣2)x2﹣3x+m2﹣4=0的一个根为0,则m=________.
17.在实数范围内定义运算“★”,其规则为a★b=a2﹣b2,则方程(4★3)★x=13的根为________.
18.关于x的一元二次方程x2+bx+c=0的两根为x1=﹣1,x2=2,则x2+bx+c可分解为________.
19.如果关于x的方程x2+2(a+1)x+2a+1=0有一个小于1的正数根,那么实数a的取值范围是________.
20.已知α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足,则m的值是________ .
三、解答题(共8题;共60分)
21.解下列方程
(1)2x2-x=0 (2)x2-4x=4
22.如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.
23.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售量,增加利润,尽快减少库存,商场决定采取适当的降价措施,经市场调查发现,如果每件衬衫降价1元,那么商场平均每天可多售出2件,若商场想平均每天盈利达1200元,那么买件衬衫应降价多少元?
24.如图,利用一面长度为7米的墙,用20米长的篱笆能否围出一个面积为48平方米的矩形菜园?若能,求出该菜园与墙平行一边的长度;若不能,说明理由.
25.随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,国家卫计委通过严打药品销售环节中的不正当行为,某种药品原价200元/瓶,经过连续两次降价后,现在仅卖98元/瓶,现假定两次降价的百分率相同,求该种药品平均每场降价的百分率.
26.阅读题:一元二次方程ax2+bx+c=0(其中a≠0,c≠0)的二根为x1和x2,请构造一个新的一元二次方程,使方程的二根适是原方程二根的3倍.数学老师张老师给出了一种方法是:设新方程的根是y,则y=3x,得x=代入原方程得变形得ay2+3by+9c=0此方程即为所求,这种利用方程根的代换求方程的方法叫换根法.解答:
(1)已知方程x2+x﹣2=0,求一个新方程使它的根分别是已知方程的相反数,所求方程为.
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0),求一个一元二次方程,使它的根分别是原方程根的倒数.
27.已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?
28.如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
答案解析部分
一、单选题
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】A
二、填空题
11.【答案】x1=0,x2=1
12.【答案】0
13.【答案】a>0
14.【答案】2013
15.【答案】10
16.【答案】﹣2
17.【答案】x1=6,x2=﹣6
18.【答案】(x+1)(x﹣2)
19.【答案】-1<a<-
20.【答案】3
三、解答题
21.【答案】(1)解:2x2-x=0,
2x(x-1)=0,
2x=0或x-1=0,
则x1=0,x2=1.
(2)解:方程两边同时+4,得x2-4x+4=4+4,
(x-2)2=8,
x-2=±2 ,
则x1=2+2 ,x2=2-2 .
22.【答案】解:设此时通道的宽为x米,根据题意,得
60×40﹣(60﹣2x)(40﹣2x)= ×60×40,
解得x=5或45,
45不合题意,舍去.
答:此时通道的宽为5米
23.【答案】解:设买件衬衫应降价x元,由题意得:(40﹣x)(20+2x)=1200,
即2x2﹣60x+400=0,
∴x2﹣30x+200=0,
∴(x﹣10)(x﹣20)=0,
解得:x=10或x=20
为了减少库存,所以x=20.
故买件衬衫应应降价20元
24.【答案】
25.【答案】解:设该种药品平均每场降价的百分率是x,由题意得:
解得:(不合题意舍去), =30%.
答:该种药品平均每场降价的百分率是30%.
26.【答案】解:(1)设所求方程的根为y,则y=﹣x,则x=﹣y.
把x=﹣y代入已知方程x2+x﹣2=0,
得(﹣y)2+(﹣y)﹣2=0.
化简得:y2﹣y﹣2=0.
故答案是:y2﹣y﹣2=0.
(2)设所求方程的根为y,则y=,所以x=,
把x=代入已知方程ax2+bx+c=0(a≠0)得
a()2+b +c=0,
去分母,得 a+by+cy2=0.
若c=0,则ax2+bx=0,于是方程ax2+bx+c=0(a≠0)有一根为0,不符合题意.
∴c≠0,
故所求的方程为:cy2+by+c=0(c≠0).
27.【答案】解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=3﹣t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ= BP,
即t= (3﹣t),t=1(秒),
当∠BPQ=90°时,BP= BQ,
3﹣t= t,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形
28.【答案】(1)解:如图1,作DE⊥BC于E,则四边形ADEB是矩形.
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴DC= =5厘米;
(2)解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴ = ,即 = ,
∴QH= t,
∴S△PQC= PC QH= (5﹣t) t=﹣ t2+3t,
S四边形ABCD= (AD+BC) AB= (1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,
﹣ t2+3t= ×9,即t2﹣5t+5=0,
解得t1= ,t2= (舍去);
②S△PQC:S四边形ABCD=2:3时,
﹣ t2+3t= ×9,即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
