简单立体几何体的面积和体积
图片预览





文档简介
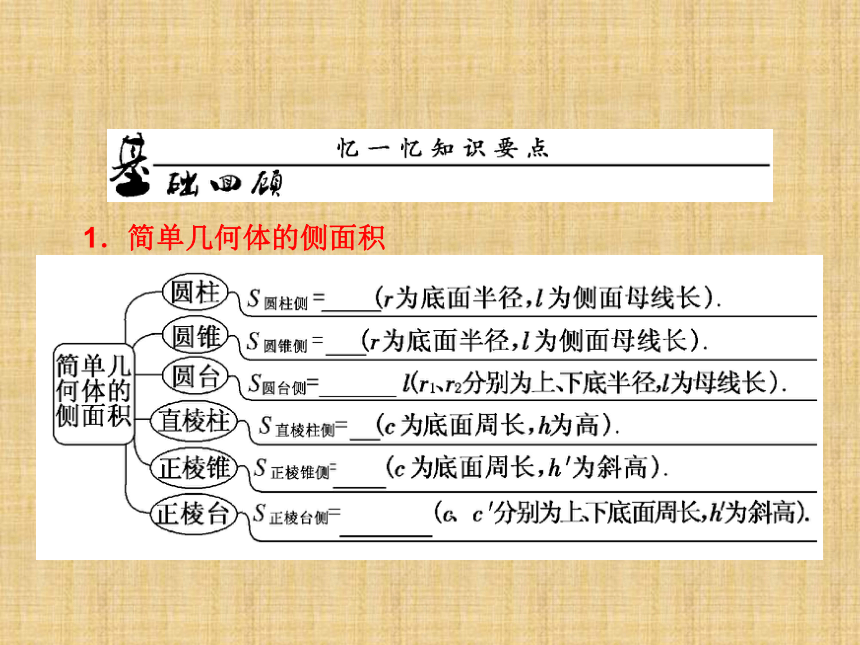
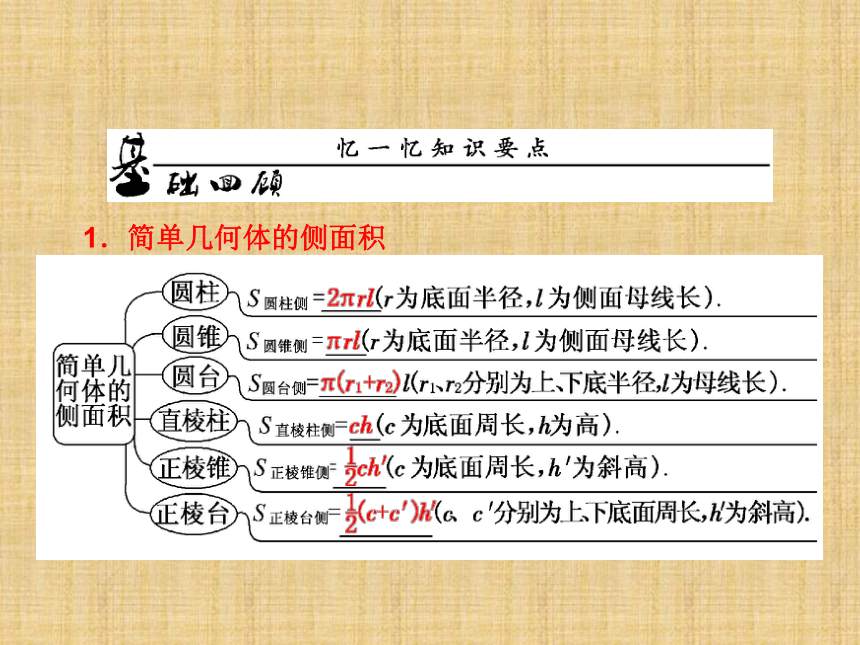
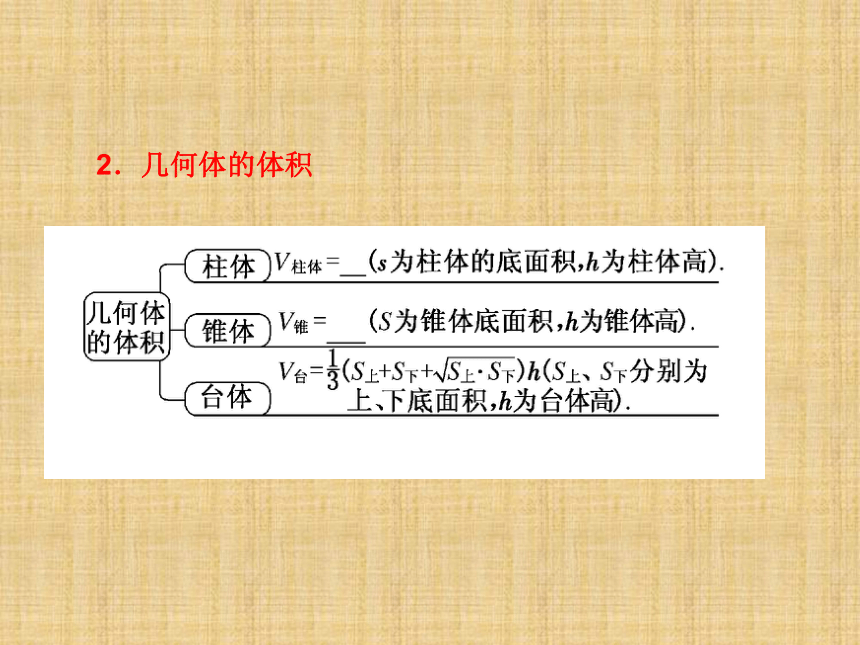
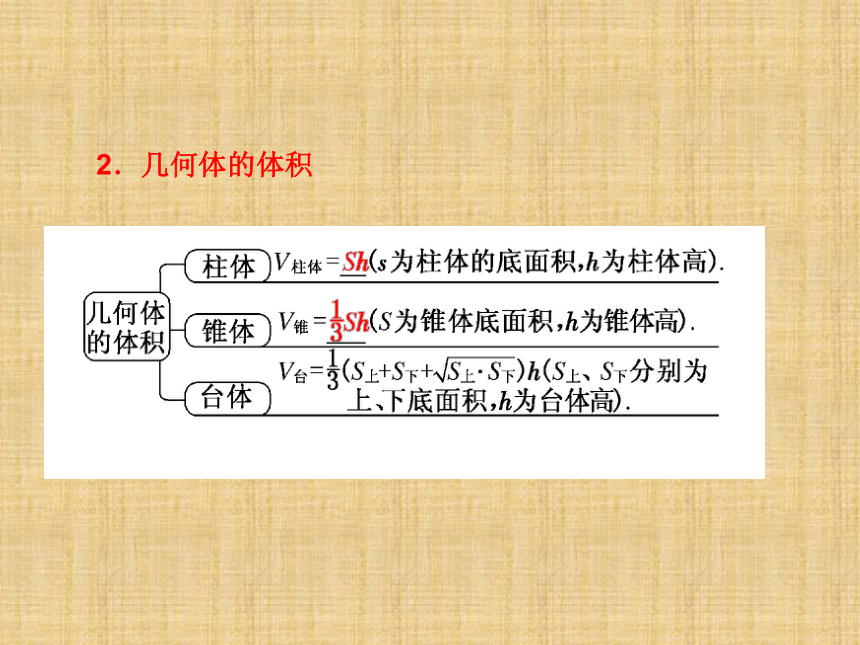
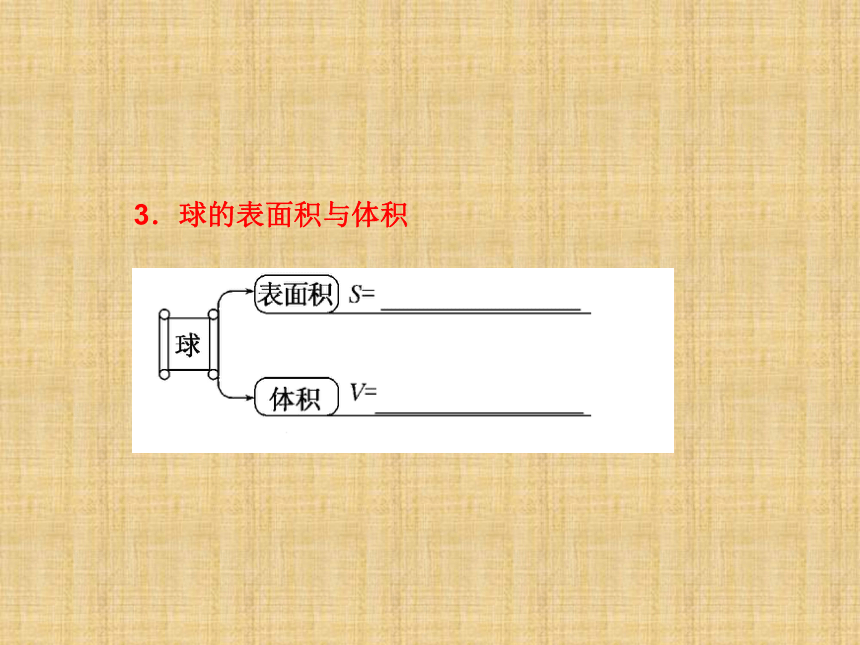
课件46张PPT。1.简单几何体的侧面积1.简单几何体的侧面积2.几何体的体积2.几何体的体积3.球的表面积与体积[思考探究]
(1)如何求简单几何体的表面积?(2)如何求不规则几何体的体积?2.圆柱的一个底面积是S,侧面展开图是一个正方形,那
么这个圆柱的侧面积是 ( )
A.4πS B.2πS
C.πS D. πS
2.圆柱的一个底面积是S,侧面展开图是一个正方形,那
么这个圆柱的侧面积是 ( )
A.4πS B.2πS
C.πS D. πS
解析:底面半径是 ,所以正方形的边长是2π
=2 ,故圆柱的侧面积是(2 )2=4πS.
答案:A
3.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,
则三棱锥D-ABC的体积为 ( )
A. B.
C. a3 D. a3
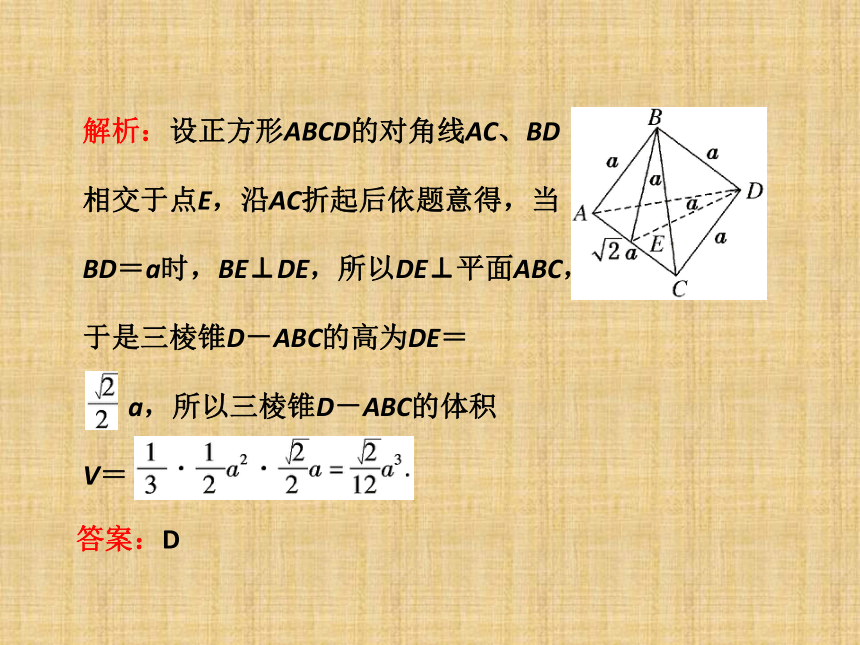
解析:设正方形ABCD的对角线AC、BD相交于点E,沿AC折起后依题意得,当BD=a时,BE⊥DE,所以DE⊥平面ABC,于是三棱锥D-ABC的高为DE=
a,所以三棱锥D-ABC的体积
V=
答案:D
4.若棱长为3的正方体的顶点都在同一球面上,则该球
的表面积为 .
4.若棱长为3的正方体的顶点都在同一球面上,则该球
的表面积为 .
解析:正方体的体对角线为球的直径.
答案:27π
5.已知一个几何体的三视图如图所示,则此几何体的体积
是 .解析:此几何体为一圆锥与圆柱的组合体.
圆柱底面半径为r=a,高为h1=2a,
圆锥底面半径为r=a,高为h2=a.
故组合体体积为V=πr2h1+ πr2h2=2πa3+ πa3
= .
答案:
求解有关棱柱、棱锥、棱台等多面体的表面积的关键是利用几何图形的性质找到其几何图形特征,从而体现出高、斜高、边长等几何元素间的关系,如棱柱中的矩形、棱锥中的直角三角形、棱台中的直角梯形等.
(2009·宁夏、海南高考)一个棱锥的三视图如图,则该棱锥的表面积(单位:cm2)为 ( )
A.48+12 B.48+24
C.36+12 D.36+24[思路点拨]
[课堂笔记] 如图所示三棱锥.
AO⊥底面BCD,O点为BD的中点,BC=CD=6 (cm),
BC⊥CD,AO=4 (cm),AB=AD.S△BCD=6×6× =18 (cm2),
S△ABD= ×6 ×4=12 (cm2).
取BC中点为E.连结AE、OE.可得AO⊥OE,
AE= = =5 (cm),
∴S△ABC=S△ACD= ×6×5=15 (cm2),
∴S表=18+12 +15+15=(48+12 ) (cm2).
[答案] A
1.柱体、锥体、台体的体积公式之间有如下关系,用图
表示如下:2.求锥体的体积,要选择适当的底面和高,然后应用公
式V= Sh进行计算即可.常用方法为:割补法和等体
积变换法:
(1)割补法:求一个几何体的体积可以将这个几何体分
割成几个柱体、锥体,分别求出锥体和柱体的体积,
从而得出几何体的体积.
(2)等体积变换法:利用三棱锥的任一个面可作为三棱锥
的底面.
①求体积时,可选择容易计算的方式来计算;
②利用“等积性”可求“点到面的距离”.
(2009·辽宁高考)正六棱锥P-ABCDEF中,G为PB的中点.则三棱锥D-GAC与三棱锥P-GAC体积之比为 ( )
A.1∶1 B.1∶2
C.2∶1 D.3∶2
[思路点拨]
[课堂笔记] ∵G为PB中点,
∴VP-GAC=VP-ABC-VG-ABC
=2VG-ABC-VG-ABC=VG-ABC.
又多边形ABCDEF是正六边形,
∴S△ABC= S△ACD,
∴VD-GAC=VG-ACD=2VG-ABC,
∴VD-GAC∶VP-GAC=2∶1.
[答案] C
1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的
面积,因此弄清侧面展开图的形状及侧面展开图中各
线段与原几何体的关系是掌握它们的面积公式及解决
相关问题的关键.
2.计算柱体、锥体、台体的体积关键是根据条件找出相
应的底面积和高,要充分利用多面体的截面及旋转体
的轴截面,将空间 如图所示,半径为R的半圆内
的阴影部分以直径AB所在直线为轴,
旋转一周得到一几何体,求该几何
体的表面积(其中∠BAC=30°).
[思路点拨]
[课堂笔记] 如图所示,过C作CO1
⊥AB于O1,
在半圆中可得∠BCA=90°,∠BAC
=30°,AB=2R,
∴AC= R,BC=R,CO1= R,
∴S球=4πR2, =π× R× R= πR2,
=π× R×R= πR2,
∴S几何体表=S球+ +
=4πR2+ πR2+ πR2= πR2.
∴旋转所得几何体的表面积为 πR2.
能否求出该几何体的体积?
= πR3- πO1C2(AO1+BO1)
= πR3- π×( R)2·2R
= πR3- πR3= πR3.
解:V几何体=V球-
= πR3- πO1C2·AO1- πO1C2·BO1
几何体的折叠与展开问题是立体几何的重要内容之一,解决折叠与展开问题的关键是弄清折叠与展开前后位置关系和数量关系的变化情况,从而画出准确的图形解决问题.2009年全国高考Ⅱ中出现了正方体的折叠与展开问题,很好的考查了学生的空间想象能力以及推理能力,代表了一种考查方向.
[考题印证]
(2009·全国卷Ⅱ)纸制的正方体
的六个面根据其方位分别标记为上、
下、东、南、西、北.现在沿该正方
体的一些棱将正方体剪开、外面朝
上展平,得到右侧的平面图形,则标“△”的面的方位是
( )
A.南 B.北
C.西 D.下
【解析】 如图所示.
规律:展开图中间隔一个为相对的面.
【答案】 B [自主体验]
已知一多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该多面体的体积V= .
解析:该多面体是一个正方体和正四棱锥的组合体,正四棱锥的底面为边长为1的正方形,侧棱长为1.
由图知,OB= BD= ,SB=1,
∴SO=
∴V四棱锥=
∴V多面体=1+ .
答案:1+
2.(2009·陕西高考)若正方体的棱长为 ,则以该正方体
各个面的中心为顶点的凸多面体的体积为 ( )
A. B.
C. D.
解析:这个凸多面体由两个全等的正四棱锥组成,正四
棱锥的底面边长为 =1,高等于 ,所以体积V=2×
×12× = .
答案:B
3.一个圆台的两底面的面积分别为π、16π,侧面积为25π,
则这个圆台的高为 ( )
A.3 B.4
C.5 D.3.一个圆台的两底面的面积分别为π、16π,侧面积为25π,
则这个圆台的高为 ( )
A.3 B.4
C.5 D.解析:由圆台侧面积公式得S=π(R+r)l=π(4+1)l=25π.得l=5,故高为 =4.
答案:B
4.(2010·广州模拟)将圆心角为 ,面积为3π的扇形,作
为圆锥的侧面,则圆锥的表面积等于 .
解析:设圆锥的母线长为l,则有 × l×l=3π,
∴l=3,且圆锥的底面周长为3× =2π,故底面半径
r=1,底面积为π,从而圆锥的表面积为4π.
答案:4π
6.如图,E、F分别为正方形ABCD
的边BC、CD的中点,沿图中虚
线将边长为2的正方形折起来,
围成一个三棱锥,求此三棱锥
的体积.解:折叠起来后,B、D、C三点重合为S点,则围成
的三棱锥为S-AEF,这时SA⊥SE,SA⊥SF,SE⊥SF,
且SA=2,SE=SF=1,
所以此三棱锥的体积V= · ·1·1·2= .
(1)如何求简单几何体的表面积?(2)如何求不规则几何体的体积?2.圆柱的一个底面积是S,侧面展开图是一个正方形,那
么这个圆柱的侧面积是 ( )
A.4πS B.2πS
C.πS D. πS
2.圆柱的一个底面积是S,侧面展开图是一个正方形,那
么这个圆柱的侧面积是 ( )
A.4πS B.2πS
C.πS D. πS
解析:底面半径是 ,所以正方形的边长是2π
=2 ,故圆柱的侧面积是(2 )2=4πS.
答案:A
3.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,
则三棱锥D-ABC的体积为 ( )
A. B.
C. a3 D. a3
解析:设正方形ABCD的对角线AC、BD相交于点E,沿AC折起后依题意得,当BD=a时,BE⊥DE,所以DE⊥平面ABC,于是三棱锥D-ABC的高为DE=
a,所以三棱锥D-ABC的体积
V=
答案:D
4.若棱长为3的正方体的顶点都在同一球面上,则该球
的表面积为 .
4.若棱长为3的正方体的顶点都在同一球面上,则该球
的表面积为 .
解析:正方体的体对角线为球的直径.
答案:27π
5.已知一个几何体的三视图如图所示,则此几何体的体积
是 .解析:此几何体为一圆锥与圆柱的组合体.
圆柱底面半径为r=a,高为h1=2a,
圆锥底面半径为r=a,高为h2=a.
故组合体体积为V=πr2h1+ πr2h2=2πa3+ πa3
= .
答案:
求解有关棱柱、棱锥、棱台等多面体的表面积的关键是利用几何图形的性质找到其几何图形特征,从而体现出高、斜高、边长等几何元素间的关系,如棱柱中的矩形、棱锥中的直角三角形、棱台中的直角梯形等.
(2009·宁夏、海南高考)一个棱锥的三视图如图,则该棱锥的表面积(单位:cm2)为 ( )
A.48+12 B.48+24
C.36+12 D.36+24[思路点拨]
[课堂笔记] 如图所示三棱锥.
AO⊥底面BCD,O点为BD的中点,BC=CD=6 (cm),
BC⊥CD,AO=4 (cm),AB=AD.S△BCD=6×6× =18 (cm2),
S△ABD= ×6 ×4=12 (cm2).
取BC中点为E.连结AE、OE.可得AO⊥OE,
AE= = =5 (cm),
∴S△ABC=S△ACD= ×6×5=15 (cm2),
∴S表=18+12 +15+15=(48+12 ) (cm2).
[答案] A
1.柱体、锥体、台体的体积公式之间有如下关系,用图
表示如下:2.求锥体的体积,要选择适当的底面和高,然后应用公
式V= Sh进行计算即可.常用方法为:割补法和等体
积变换法:
(1)割补法:求一个几何体的体积可以将这个几何体分
割成几个柱体、锥体,分别求出锥体和柱体的体积,
从而得出几何体的体积.
(2)等体积变换法:利用三棱锥的任一个面可作为三棱锥
的底面.
①求体积时,可选择容易计算的方式来计算;
②利用“等积性”可求“点到面的距离”.
(2009·辽宁高考)正六棱锥P-ABCDEF中,G为PB的中点.则三棱锥D-GAC与三棱锥P-GAC体积之比为 ( )
A.1∶1 B.1∶2
C.2∶1 D.3∶2
[思路点拨]
[课堂笔记] ∵G为PB中点,
∴VP-GAC=VP-ABC-VG-ABC
=2VG-ABC-VG-ABC=VG-ABC.
又多边形ABCDEF是正六边形,
∴S△ABC= S△ACD,
∴VD-GAC=VG-ACD=2VG-ABC,
∴VD-GAC∶VP-GAC=2∶1.
[答案] C
1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的
面积,因此弄清侧面展开图的形状及侧面展开图中各
线段与原几何体的关系是掌握它们的面积公式及解决
相关问题的关键.
2.计算柱体、锥体、台体的体积关键是根据条件找出相
应的底面积和高,要充分利用多面体的截面及旋转体
的轴截面,将空间 如图所示,半径为R的半圆内
的阴影部分以直径AB所在直线为轴,
旋转一周得到一几何体,求该几何
体的表面积(其中∠BAC=30°).
[思路点拨]
[课堂笔记] 如图所示,过C作CO1
⊥AB于O1,
在半圆中可得∠BCA=90°,∠BAC
=30°,AB=2R,
∴AC= R,BC=R,CO1= R,
∴S球=4πR2, =π× R× R= πR2,
=π× R×R= πR2,
∴S几何体表=S球+ +
=4πR2+ πR2+ πR2= πR2.
∴旋转所得几何体的表面积为 πR2.
能否求出该几何体的体积?
= πR3- πO1C2(AO1+BO1)
= πR3- π×( R)2·2R
= πR3- πR3= πR3.
解:V几何体=V球-
= πR3- πO1C2·AO1- πO1C2·BO1
几何体的折叠与展开问题是立体几何的重要内容之一,解决折叠与展开问题的关键是弄清折叠与展开前后位置关系和数量关系的变化情况,从而画出准确的图形解决问题.2009年全国高考Ⅱ中出现了正方体的折叠与展开问题,很好的考查了学生的空间想象能力以及推理能力,代表了一种考查方向.
[考题印证]
(2009·全国卷Ⅱ)纸制的正方体
的六个面根据其方位分别标记为上、
下、东、南、西、北.现在沿该正方
体的一些棱将正方体剪开、外面朝
上展平,得到右侧的平面图形,则标“△”的面的方位是
( )
A.南 B.北
C.西 D.下
【解析】 如图所示.
规律:展开图中间隔一个为相对的面.
【答案】 B [自主体验]
已知一多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该多面体的体积V= .
解析:该多面体是一个正方体和正四棱锥的组合体,正四棱锥的底面为边长为1的正方形,侧棱长为1.
由图知,OB= BD= ,SB=1,
∴SO=
∴V四棱锥=
∴V多面体=1+ .
答案:1+
2.(2009·陕西高考)若正方体的棱长为 ,则以该正方体
各个面的中心为顶点的凸多面体的体积为 ( )
A. B.
C. D.
解析:这个凸多面体由两个全等的正四棱锥组成,正四
棱锥的底面边长为 =1,高等于 ,所以体积V=2×
×12× = .
答案:B
3.一个圆台的两底面的面积分别为π、16π,侧面积为25π,
则这个圆台的高为 ( )
A.3 B.4
C.5 D.3.一个圆台的两底面的面积分别为π、16π,侧面积为25π,
则这个圆台的高为 ( )
A.3 B.4
C.5 D.解析:由圆台侧面积公式得S=π(R+r)l=π(4+1)l=25π.得l=5,故高为 =4.
答案:B
4.(2010·广州模拟)将圆心角为 ,面积为3π的扇形,作
为圆锥的侧面,则圆锥的表面积等于 .
解析:设圆锥的母线长为l,则有 × l×l=3π,
∴l=3,且圆锥的底面周长为3× =2π,故底面半径
r=1,底面积为π,从而圆锥的表面积为4π.
答案:4π
6.如图,E、F分别为正方形ABCD
的边BC、CD的中点,沿图中虚
线将边长为2的正方形折起来,
围成一个三棱锥,求此三棱锥
的体积.解:折叠起来后,B、D、C三点重合为S点,则围成
的三棱锥为S-AEF,这时SA⊥SE,SA⊥SF,SE⊥SF,
且SA=2,SE=SF=1,
所以此三棱锥的体积V= · ·1·1·2= .
