2022年新教材高中数学第一章集合与常用逻辑用语2.3充分条件必要条件课件新人教B版必修第一册 课件 (共25张PPT)
文档属性
| 名称 | 2022年新教材高中数学第一章集合与常用逻辑用语2.3充分条件必要条件课件新人教B版必修第一册 课件 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 378.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-24 10:11:06 | ||
图片预览







文档简介
(共25张PPT)
1.2.3 充分条件、必要条件
1.根据实例理解充分条件、必要条件与充要条件的含义.
2.结合具体命题掌握判断充分条件、必要条件与充要条件的方法.
3.会用集合的知识来理解充分条件、必要条件与充要条件.
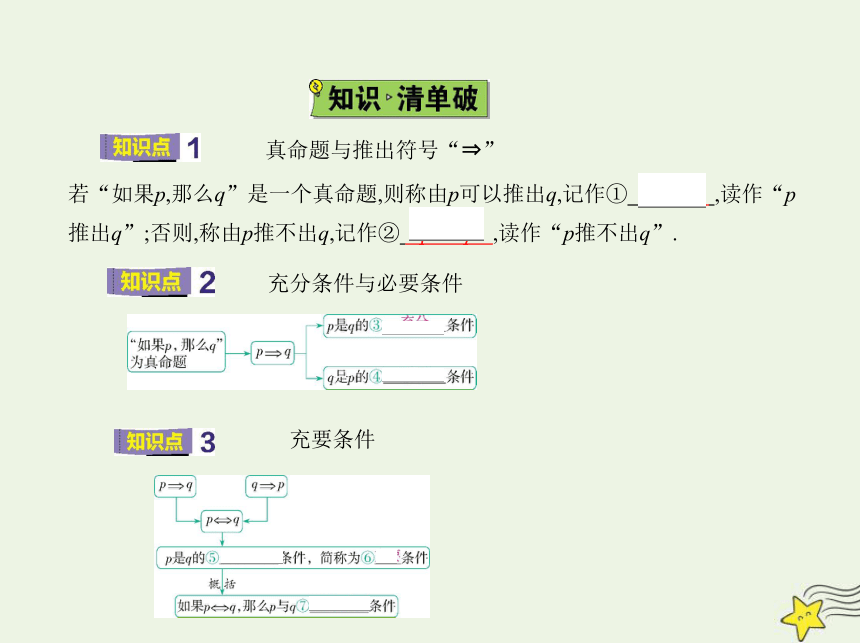
真命题与推出符号“ ”
若“如果p,那么q”是一个真命题,则称由p可以推出q,记作① p q ,读作“p
推出q”;否则,称由p推不出q,记作② p /q ,读作“p推不出q”.
充分条件与必要条件
充要条件
用集合知识理解充分条件、必要条件、充要条件
一般地,如果A={x|p(x)},B={x|q(x)},且A B,那么p(x) q(x),因此也就有p(x)是
q(x)的⑧ 充分条件 ,q(x)是p(x)的⑨ 必要条件 .
如果A=B,那么⑩ p(x) q(x) ,因此p(x)是q(x)的 充要条件 .
.
判断正误,正确的画“√”,错误的画“ ”.
1.x>1是x2>1的充分条件. ( √ )
2.“△ABC是等腰三角形”是 “A=B”的充要条件. ( )
3.a,b∈R,ab=0是a2+b2=0的必要条件. ( √ )
4.集合A={x|x>1},B={x|x>2},则x∈A是x∈B的充分条件. ( )
x>2 x>1,即B A,所以x∈B是x∈A的充分条件,x∈A是x∈B的必要条件.
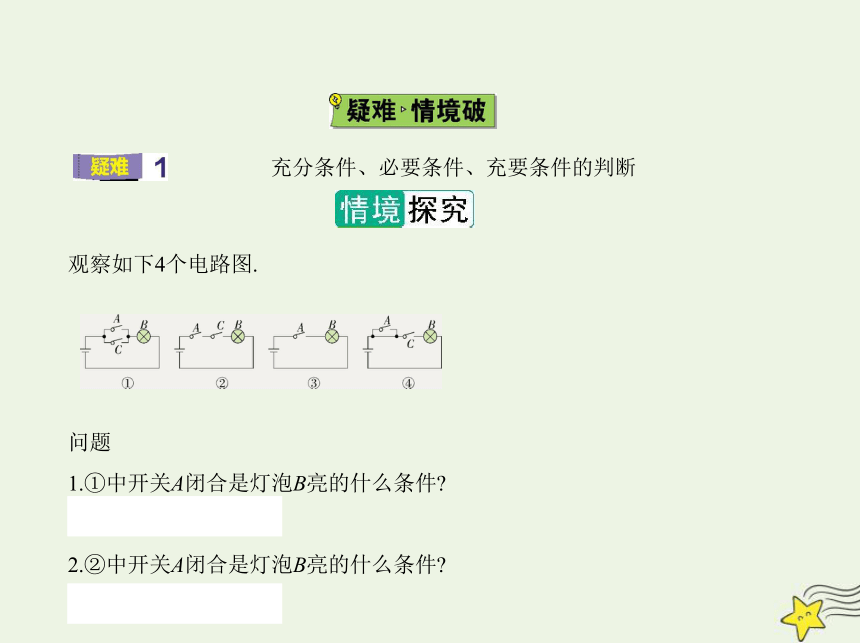
观察如下4个电路图.
问题
1.①中开关A闭合是灯泡B亮的什么条件
提示:充分不必要条件.
2.②中开关A闭合是灯泡B亮的什么条件
提示:必要不充分条件.
充分条件、必要条件、充要条件的判断
3.③中开关A闭合是灯泡B亮的什么条件
提示:充要条件.
4.④中开关A闭合是灯泡B亮的什么条件
提示:既不充分也不必要条件.
充分、必要条件的判断主要有以下几种方法
(1)定义法:直接利用定义进行判断.
(2)等价法:“p q”表示p等价于q,等价命题可以进行转换,当我们要证明p成立
时,就可以去证明q成立.
(3)传递法:根据充分、必要关系的传递性来判断的方法叫传递法.充分条件具有
传递性,若A1 A2 A3 … An-1 An,则A1 An,即A1是An的充分条件.必要条件也
有传递性,若A1 A2 A3 … An-1 An,则A1 An,即A1是An的必要条件.当然充要
条件也有传递性.因此,对于较复杂(连锁式)的充要关系的判断可用连锁式的传递
图来解答.
(4)利用集合间的包含关系进行判断:如果条件p和结论q组成的集合分别为A、B,
那么若A B,则p是q的充分条件;若B A,则p是q的必要条件;若A=B,则p既是q的
充分条件,又是q的必要条件. 若A B,则p是q的充分不必要条件;若A B且B A,
则p是q的既不充分也不必要条件.
拔高问题
5.将①中开关A与灯泡B的位置互换,开关C始终是断开状态,结论变为什么
提示:变为充要条件.
破疑典例
1.( )已知p,q都是r的必要条件,s是r的充分条件,q是s的充分条件.那么:
(1)s是q的什么条件
(2)r是q的什么条件
(3)p是q的什么条件
思路点拨:
利用充分条件、必要条件的定义来判断.
解析 由已知可得r p,r q,
s r,q s.
(1)∵q s r q,即s q,
∴s是q的充要条件.
(2)∵q s r q,即r q,
∴r是q的充要条件.
(3)∵q s r p,即q p,
∴p是q的必要条件.
2.( ) 在以下各题中,判断p是q的什么条件.
(1)p:x>4且y>5,q:x+y>9;
(2)p:两个三角形全等,q:两个三角形相似;
(3)p:一个四边形的四个角都相等,q:四边形是正方形;
(4)p:(x-2)(x-3)=0,q:x-2=0;
(5)p:a是素数,q:a不是偶数.
思路点拨:
要判断p与q的关系,主要是看p能否推出q,q能否推出p.
解析 (1)由于p q,q / p,故p是q的充分不必要条件.
(2)∵两个三角形全等能推出两个三角形相似,而两个三角形相似不能推出两个
三角形全等,∴p是q的充分不必要条件.
(3)由于q p,p / q,故p是q的必要不充分条件.
(4)∵(x-2)(x-3)=0,∴x=2或x=3,不能推出x-2=0,但由x-2=0可推出(x-2)(x-3)=0,
∴p是q的必要不充分条件.
(5)p是q的既不充分也不必要条件.
陷阱分析 要分清谁是条件,谁是结论,不要混淆.
已知p:x=1,q:x2-2x+1=0,如何判定p是q的什么条件
问题
1.p是不是q的充分条件
提示:由x=1能推出x2-2x+1=0,因此p是q的充分条件.
2.p是不是q的必要条件
提示:由x2-2x+1=(x-1)2=0能推出x=1,因此p是q的必要条件.
3.p是不是q的充要条件
提示:p是q的充分条件,且p是q的必要条件,因此p是q的充要条件.
充分条件、必要条件的证明与探究
判断与证明充要条件,一要判断条件是否能推出结论,即p q是否成立,若成立,则
p是q的充分条件,否则不是充分条件;二要判断结论是否能推出条件,即q p是否
成立,若成立,则p是q的必要条件,否则不是必要条件;若既是充分条件又是必要条
件,就判断为充要条件.
关于充分条件、必要条件、充要条件,当不容易判断p q及q p的真假时,也可
以从集合角度去判断,结合集合中的关系来理解,这对解决与逻辑有关的问题是
大有益处的.
拔高问题
4.设U是全集,p:A∩B=A,q: UB UA,如何证明p是q的充要条件
提示:充分性:若A∩B=A,则A B,画出维恩图(图略),由图可得 UB UA,因此p是
q的充分条件;
必要性:若 UB UA,画出维恩图(图略),可得A B,则A∩B=A,因此p是q的必要
条件.
因此p是q的充要条件.
5.如何证明函数y=x2+mx+1的图像关于直线x=1对称的充要条件是m=-2
提示:当m=-2时,y=x2-2x+1,其图像关于直线x=1对称,反之也成立,所以函数y=x2+mx
+1的图像关于直线x=1对称的充要条件是m=-2.
破疑典例
1.( )命题:“y=kx2-kx-1的函数值恒为负”成立的充要条件是 .
思路点拨:
“将y=kx2-kx-1的函数值恒为负”看作条件,并由此推导等价结论即为充要
条件.
答案 -4解析 当k=0时,y=-1<0恒成立.
当k<0时,y<0恒成立 Δ=k2+4k<0 -4综上,充要条件为-42.( )已知ab≠0,求证:a3+b3+ab-a2-b2=0成立的充要条件是a+b=1.
思路点拨:
先证明充分性,即证a+b=1 a3+b3+ab-a2-b2=0,再证明必要性,即证a3+b3+ab-a2-
b2=0 a+b=1.
证明 充分性:若a+b=1,
则b=1-a.
∴a3+b3+ab-a2-b2=a3+(1-a)3+a(1-a)-a2-(1-a)2=a3+1-3a+3a2-a3+a-a2-a2-1+2a-a2=0.
必要性:
∵a3+b3+ab-a2-b2
=(a+b)(a2-ab+b2)-(a2-ab+b2)
=(a+b-1)(a2-ab+b2)=0,
又ab≠0,
∴a2-ab+b2≠0,∴a+b-1=0,
即a+b=1.
综上,a3+b3+ab-a2-b2=0成立的充要条件是a+b=1.
易错警示 证明充要条件,要将充分性与必要性分开证明,解题时要防止将充分
性与必要性证反导致解题错误,其关键是分清条件与结论.
已知集合A={x|x>1},B={x|x>a}.
问题
1.若A B,如何求实数a的取值范围
提示:因为A B,所以a<1,即实数a的取值范围是a<1.
2.若“x∈A”是“x∈B”的充分不必要条件,则集合A与B是什么关系
提示:由充分不必要条件的定义可知,若x∈A,则x∈B一定成立,但若x∈B,则x∈A
不一定成立,所以A B.
3.若“x∈A”是“x∈B”的必要不充分条件,如何确定实数a的取值范围
提示:由必要不充分条件的定义可知,若x∈B,则x∈A一定成立,但若x∈A,则x∈B
不一定成立,所以B A.因此a>1,即实数a的取值范围是a>1.
利用充分条件、必要条件确定参数的值(取值范围)
充分条件、必要条件的应用一般表现在参数问题的求解上.解题时需注意:(1)把
充分条件、必要条件转化为集合之间的关系,然后根据集合之间的关系列出关于
参数的等式或不等式(组)求解.(2)要注意端点值的检验.
拔高问题
4.已知p:x∈{x|4x+m<0},q:x∈{x|x>2或x<-1},若p是q的充分条件,如何求实数m的
取值范围
提示:令A={x|x>2或x<-1},
B={x|4x+m<0}.
由4x+m<0,得B= .当B A时,- ≤-1,即m≥4,
故若p是q的充分条件,则m≥4.
破疑典例
1.( )集合A=
≤2 ,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分不必要条件,求实数m的取值围.
思路点拨:
“x∈A”是“x∈B”的充分不必要条件 A B 得出关于m的不等式
解出m的取值范围.
解析 A= y y=x2- x+1, ≤x≤2 = ,B={x|x+m2≥1}={x|x≥1-m2},
∵“x∈A”是“x∈B”的充分不必要条件,
∴A B,
∴1-m2≤ ,
解得m≥ 或m≤- ,
故m的取值范围为m≤- 或m≥ .
2.( )已知p:-2≤1- ≤2,q:x2-2x+1-m2≤0(m>0),且 p是 q的必要不充分条
件,求实数m的取值范围.
思路点拨:
求出 p, q对应的集合 由 p是 q的必要不充分条件得出集合间的关系
建立关于m的不等式 解出m的取值范围.
解析 由-2≤1- ≤2,解得-2≤x≤10,
∴ p:B={x|x>10或x<-2}.
由x2-2x+1-m2≤0(m>0),
解得1-m≤x≤m+1,
∴ q:A={x|x<1-m或x>m+1}.
∵ p是 q的必要不充分条件,
∴A B ,
或 解得m≥9.
∴实数m的取值范围是{m|m≥9}.
1.2.3 充分条件、必要条件
1.根据实例理解充分条件、必要条件与充要条件的含义.
2.结合具体命题掌握判断充分条件、必要条件与充要条件的方法.
3.会用集合的知识来理解充分条件、必要条件与充要条件.
真命题与推出符号“ ”
若“如果p,那么q”是一个真命题,则称由p可以推出q,记作① p q ,读作“p
推出q”;否则,称由p推不出q,记作② p /q ,读作“p推不出q”.
充分条件与必要条件
充要条件
用集合知识理解充分条件、必要条件、充要条件
一般地,如果A={x|p(x)},B={x|q(x)},且A B,那么p(x) q(x),因此也就有p(x)是
q(x)的⑧ 充分条件 ,q(x)是p(x)的⑨ 必要条件 .
如果A=B,那么⑩ p(x) q(x) ,因此p(x)是q(x)的 充要条件 .
.
判断正误,正确的画“√”,错误的画“ ”.
1.x>1是x2>1的充分条件. ( √ )
2.“△ABC是等腰三角形”是 “A=B”的充要条件. ( )
3.a,b∈R,ab=0是a2+b2=0的必要条件. ( √ )
4.集合A={x|x>1},B={x|x>2},则x∈A是x∈B的充分条件. ( )
x>2 x>1,即B A,所以x∈B是x∈A的充分条件,x∈A是x∈B的必要条件.
观察如下4个电路图.
问题
1.①中开关A闭合是灯泡B亮的什么条件
提示:充分不必要条件.
2.②中开关A闭合是灯泡B亮的什么条件
提示:必要不充分条件.
充分条件、必要条件、充要条件的判断
3.③中开关A闭合是灯泡B亮的什么条件
提示:充要条件.
4.④中开关A闭合是灯泡B亮的什么条件
提示:既不充分也不必要条件.
充分、必要条件的判断主要有以下几种方法
(1)定义法:直接利用定义进行判断.
(2)等价法:“p q”表示p等价于q,等价命题可以进行转换,当我们要证明p成立
时,就可以去证明q成立.
(3)传递法:根据充分、必要关系的传递性来判断的方法叫传递法.充分条件具有
传递性,若A1 A2 A3 … An-1 An,则A1 An,即A1是An的充分条件.必要条件也
有传递性,若A1 A2 A3 … An-1 An,则A1 An,即A1是An的必要条件.当然充要
条件也有传递性.因此,对于较复杂(连锁式)的充要关系的判断可用连锁式的传递
图来解答.
(4)利用集合间的包含关系进行判断:如果条件p和结论q组成的集合分别为A、B,
那么若A B,则p是q的充分条件;若B A,则p是q的必要条件;若A=B,则p既是q的
充分条件,又是q的必要条件. 若A B,则p是q的充分不必要条件;若A B且B A,
则p是q的既不充分也不必要条件.
拔高问题
5.将①中开关A与灯泡B的位置互换,开关C始终是断开状态,结论变为什么
提示:变为充要条件.
破疑典例
1.( )已知p,q都是r的必要条件,s是r的充分条件,q是s的充分条件.那么:
(1)s是q的什么条件
(2)r是q的什么条件
(3)p是q的什么条件
思路点拨:
利用充分条件、必要条件的定义来判断.
解析 由已知可得r p,r q,
s r,q s.
(1)∵q s r q,即s q,
∴s是q的充要条件.
(2)∵q s r q,即r q,
∴r是q的充要条件.
(3)∵q s r p,即q p,
∴p是q的必要条件.
2.( ) 在以下各题中,判断p是q的什么条件.
(1)p:x>4且y>5,q:x+y>9;
(2)p:两个三角形全等,q:两个三角形相似;
(3)p:一个四边形的四个角都相等,q:四边形是正方形;
(4)p:(x-2)(x-3)=0,q:x-2=0;
(5)p:a是素数,q:a不是偶数.
思路点拨:
要判断p与q的关系,主要是看p能否推出q,q能否推出p.
解析 (1)由于p q,q / p,故p是q的充分不必要条件.
(2)∵两个三角形全等能推出两个三角形相似,而两个三角形相似不能推出两个
三角形全等,∴p是q的充分不必要条件.
(3)由于q p,p / q,故p是q的必要不充分条件.
(4)∵(x-2)(x-3)=0,∴x=2或x=3,不能推出x-2=0,但由x-2=0可推出(x-2)(x-3)=0,
∴p是q的必要不充分条件.
(5)p是q的既不充分也不必要条件.
陷阱分析 要分清谁是条件,谁是结论,不要混淆.
已知p:x=1,q:x2-2x+1=0,如何判定p是q的什么条件
问题
1.p是不是q的充分条件
提示:由x=1能推出x2-2x+1=0,因此p是q的充分条件.
2.p是不是q的必要条件
提示:由x2-2x+1=(x-1)2=0能推出x=1,因此p是q的必要条件.
3.p是不是q的充要条件
提示:p是q的充分条件,且p是q的必要条件,因此p是q的充要条件.
充分条件、必要条件的证明与探究
判断与证明充要条件,一要判断条件是否能推出结论,即p q是否成立,若成立,则
p是q的充分条件,否则不是充分条件;二要判断结论是否能推出条件,即q p是否
成立,若成立,则p是q的必要条件,否则不是必要条件;若既是充分条件又是必要条
件,就判断为充要条件.
关于充分条件、必要条件、充要条件,当不容易判断p q及q p的真假时,也可
以从集合角度去判断,结合集合中的关系来理解,这对解决与逻辑有关的问题是
大有益处的.
拔高问题
4.设U是全集,p:A∩B=A,q: UB UA,如何证明p是q的充要条件
提示:充分性:若A∩B=A,则A B,画出维恩图(图略),由图可得 UB UA,因此p是
q的充分条件;
必要性:若 UB UA,画出维恩图(图略),可得A B,则A∩B=A,因此p是q的必要
条件.
因此p是q的充要条件.
5.如何证明函数y=x2+mx+1的图像关于直线x=1对称的充要条件是m=-2
提示:当m=-2时,y=x2-2x+1,其图像关于直线x=1对称,反之也成立,所以函数y=x2+mx
+1的图像关于直线x=1对称的充要条件是m=-2.
破疑典例
1.( )命题:“y=kx2-kx-1的函数值恒为负”成立的充要条件是 .
思路点拨:
“将y=kx2-kx-1的函数值恒为负”看作条件,并由此推导等价结论即为充要
条件.
答案 -4
当k<0时,y<0恒成立 Δ=k2+4k<0 -4
思路点拨:
先证明充分性,即证a+b=1 a3+b3+ab-a2-b2=0,再证明必要性,即证a3+b3+ab-a2-
b2=0 a+b=1.
证明 充分性:若a+b=1,
则b=1-a.
∴a3+b3+ab-a2-b2=a3+(1-a)3+a(1-a)-a2-(1-a)2=a3+1-3a+3a2-a3+a-a2-a2-1+2a-a2=0.
必要性:
∵a3+b3+ab-a2-b2
=(a+b)(a2-ab+b2)-(a2-ab+b2)
=(a+b-1)(a2-ab+b2)=0,
又ab≠0,
∴a2-ab+b2≠0,∴a+b-1=0,
即a+b=1.
综上,a3+b3+ab-a2-b2=0成立的充要条件是a+b=1.
易错警示 证明充要条件,要将充分性与必要性分开证明,解题时要防止将充分
性与必要性证反导致解题错误,其关键是分清条件与结论.
已知集合A={x|x>1},B={x|x>a}.
问题
1.若A B,如何求实数a的取值范围
提示:因为A B,所以a<1,即实数a的取值范围是a<1.
2.若“x∈A”是“x∈B”的充分不必要条件,则集合A与B是什么关系
提示:由充分不必要条件的定义可知,若x∈A,则x∈B一定成立,但若x∈B,则x∈A
不一定成立,所以A B.
3.若“x∈A”是“x∈B”的必要不充分条件,如何确定实数a的取值范围
提示:由必要不充分条件的定义可知,若x∈B,则x∈A一定成立,但若x∈A,则x∈B
不一定成立,所以B A.因此a>1,即实数a的取值范围是a>1.
利用充分条件、必要条件确定参数的值(取值范围)
充分条件、必要条件的应用一般表现在参数问题的求解上.解题时需注意:(1)把
充分条件、必要条件转化为集合之间的关系,然后根据集合之间的关系列出关于
参数的等式或不等式(组)求解.(2)要注意端点值的检验.
拔高问题
4.已知p:x∈{x|4x+m<0},q:x∈{x|x>2或x<-1},若p是q的充分条件,如何求实数m的
取值范围
提示:令A={x|x>2或x<-1},
B={x|4x+m<0}.
由4x+m<0,得B= .当B A时,- ≤-1,即m≥4,
故若p是q的充分条件,则m≥4.
破疑典例
1.( )集合A=
≤2 ,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分不必要条件,求实数m的取值围.
思路点拨:
“x∈A”是“x∈B”的充分不必要条件 A B 得出关于m的不等式
解出m的取值范围.
解析 A= y y=x2- x+1, ≤x≤2 = ,B={x|x+m2≥1}={x|x≥1-m2},
∵“x∈A”是“x∈B”的充分不必要条件,
∴A B,
∴1-m2≤ ,
解得m≥ 或m≤- ,
故m的取值范围为m≤- 或m≥ .
2.( )已知p:-2≤1- ≤2,q:x2-2x+1-m2≤0(m>0),且 p是 q的必要不充分条
件,求实数m的取值范围.
思路点拨:
求出 p, q对应的集合 由 p是 q的必要不充分条件得出集合间的关系
建立关于m的不等式 解出m的取值范围.
解析 由-2≤1- ≤2,解得-2≤x≤10,
∴ p:B={x|x>10或x<-2}.
由x2-2x+1-m2≤0(m>0),
解得1-m≤x≤m+1,
∴ q:A={x|x<1-m或x>m+1}.
∵ p是 q的必要不充分条件,
∴A B ,
或 解得m≥9.
∴实数m的取值范围是{m|m≥9}.
