八年级上册1.4等腰三角形（1）

课件17张PPT。创设情境：在前面的学习中，我们认识了轴对称图形，探究了轴对称的性质.这节课我们就是从轴对称的角度来认识一些我们熟悉的几何图形来研究：①三角形是轴对称图形吗？
②什么样的三角形是轴对称图形？ 有的三角形是轴对称图形，有的三角形不是．
问题：那什么样的三角形是轴对称图形呢？
满足轴对称的条件的三角形就是轴对称图形,也就是将三角形沿某一条直线对折后两部分能够完全重合的就是轴对称图形．
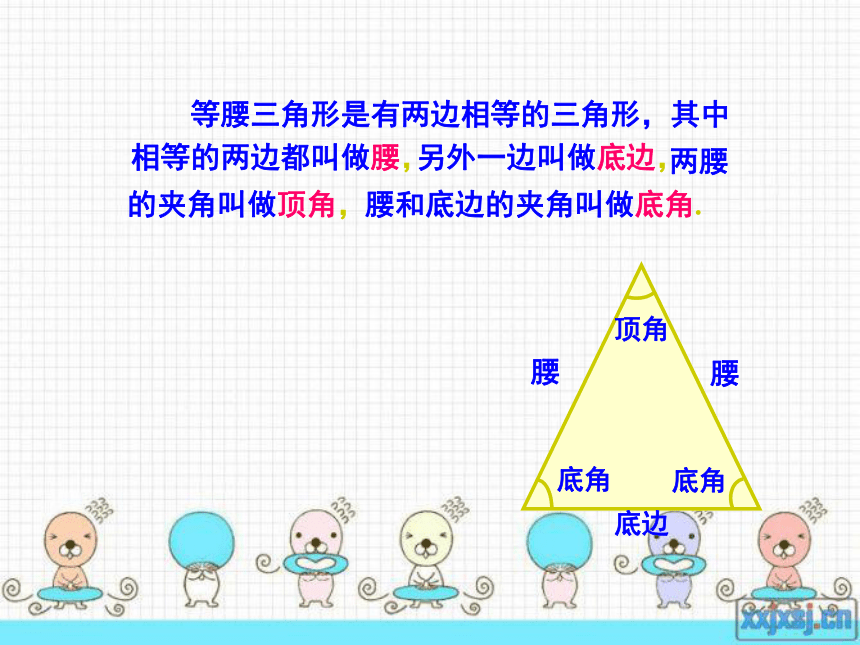
我们这节课就来认识一种成轴对称图形的三角形──等腰三角形． 等腰三角形是有两边相等的三角形，其中相等的两边都叫做腰， 另外一边叫做底边， 两腰的夹角叫做顶角， 腰和底边的夹角叫做底角. 底边思考： 1.等腰三角形是轴对称图形吗？请找出它的对称轴．
2.等腰三角形的两底角有什么关系？
3.顶角的平分线所在的直线是等腰三角形的对称轴吗？
4.底边上的中线所在的直线是等腰三角形的对称轴吗？底边上的高所在的直线 呢？结论： 等腰三角形是轴对称图形．它的对称轴是顶角的平分线所在的直线．
因为等腰三角形的两腰相等，所以把这两条腰重合对折三角形便知：等腰三角形是轴对称图形，它的对称轴是顶角的平分线所在的直线． 沿等腰三角形的顶角的平分线对折，发现它两旁的部分互相重合，由此可知这个等腰三角形的两个底角相等，而且还可以知道顶角的平分线既是底边上的中线，也是底边上的高．由此可以得到等腰三角形的性质： 1．等腰三角形的两个底角相等（简写成“等边对等角”）．
2．等腰三角形的顶角平分线，底边上的中线、底边上的高互相重合（通常称作“三线合一”）由角平分线的性质还可得到： 等腰三角形底边上的中点到两腰的距离相等.例1 如图，点D，E在△ABC的边BC上，
AB=AC，AD=AE. AF是BC边上的高.
BD与CE相等吗？为什么？解 因为AF是等腰△ABC和等腰△ADE
底边上的高，所以 BF=CF，DF=EF. 所以它也是底边上的中线．从而 BF-DF=CF-EF. 即 BD = CE. 例2 某日上午10时，一条船从A处出发以20海里/h的
速度向正北航行(如图)，中午12时到达B处.
从A，B望灯塔C，测得∠NAC=40°，∠NBC=80°，
求从B处到灯塔C的距离. 解 因为∠NBC=∠A+∠C(三角形的一个
外角等于不相邻的两个内角的和)，所以 ∠C=80°-40°=40°. 因此　BA=BC(等角对等边). 因为 AB=20×(12-10)=40(海里)，所以　BC=40海里. 答：B处到灯塔C的距离是40海里.随堂练习:课本第132页练习 1、2．1. 已知：如图，在△ABC中，BA=BC,BD是∠ABC的平分线，其中AD=4cm. 求DC的长.解：因为在△ABC中，
BA=BC，
所以△ABC是等腰三角形，
又因为BD是△ABC的平分线，
所以AD=DC，
又因为AD=4cm，
所以DC=4cm.2.如图，在△AB C中，AB=AC，点D在AC上，且BD=BC=AD，求：△ABC各角的度数．解：因为A B=AC，BD=BC=AD， 所以∠ABC=∠C=∠BDC． ∠A=∠ABD（等边对等角）． 设∠A=x，则 ∠BDC=∠A+∠ABD=2x， 从而∠ABC=∠C=∠BDC=2x． 于 是在△ABC中，有 ∠A+ ∠ABC+∠C=x+2x+2x=180°， 解得x=36°． 在△ABC中，∠A=35°， ∠ABC=∠C=72°．
小结: 这节课我们主要探讨了等腰三角形的性质，并对性质作了简单的应用．等腰三角形是轴对称图形，它的两个底角相等（等边对等角），等腰三角形的对称轴是它顶角的平分线，并且它的顶角平分线既是底边上的中线，又是底边上的高．作业:P.136 A组第1题谢谢!!!再见!!!